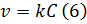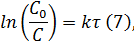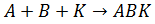ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:
(II.29)
(II.30)
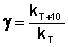
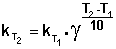
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
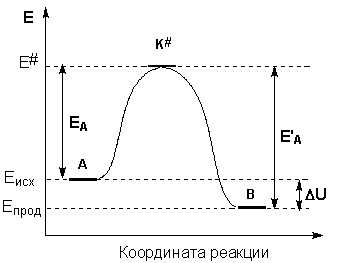
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
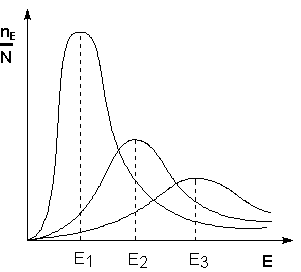
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei — средняя энергия частиц при температуре Ti (T1 уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,
(II.31)
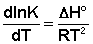
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
(II.32)
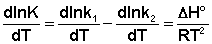
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
(II.33)
(II.34)
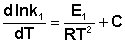
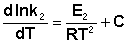
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
(II.35)
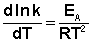
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
(II.36)
(II.37)
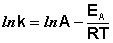
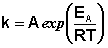
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
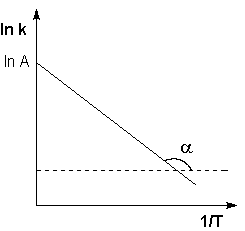
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
(II.38)
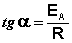
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
(II.39)
Copyright © С. И. Левченков, 1996 — 2005.
Видео:Влияние температуры на скорость химических реакций. 10 класс.Скачать
Уравнение Аррениуса. Понятие об энергии активации
Более точную но сравнению с правилом Вант-Гоффа зависимость скорости химической реакции от температуры установил шведский химик Сванте-Август Аррениус (1859—1927).
Уравнение Аррениуса описывает влияние температуры на константу скорости химической реакции к в уравнении Гульдберга и Вааге и имеет вид
или в логарифмической записи 
Здесь к <)— предэкспоненциальный множитель. По физическому смыслу эта величина отражает число активных столкновений частиц в единице объема реакционной смеси. Для большинства химических реакций второго порядка значения к0 = 10 И -И0 13 лДмоль с); ЕА — экспериментальная энергия активации.
Энергия активации — избыток энергии (но отношению к средней энергии частиц при данной температуре), который необходимо иметь частице для того, чтобы при данных условиях вступить в реакцию.
Избыток получается за счет хаотической природы температуры. При всяком среднем значении кинетической тепловой энергии в системе в ней всегда присутствуют как более медленные, так и более быстрые частицы. Те из них, у которых избыток скорости достаточно велик, и обладают нужной энергией активации. Отметим, что влияние температуры на скорость химических реакций значительно выше при низких температурах, чем при высоких. Экспоненциальный множитель в уравнении Аррениуса выражает ту долю частиц, у которых энергия равна или больше энергии активации. Энергия активации выражается в энергетических единицах, отнесенных к одному молю реагирующих частиц, и имеет размерность [кДж/моль].
Исходя из логарифмической формулы уравнения Аррениуса часто находят экспериментальную энергию активации, построив график зависимости 1п& =/(1/7) (рис. 12.3).
По экспериментальным точкам строится прямая, которая отсекает на оси ординат отрезок, равный 1п к0, а угол а связан с энергией активации ЕА соотношением
При этом нужно помнить, что Еа — величина размерная, поэтому для расчета tga нужно брать не геометрические отрезки на рисунке, а их размерные значения из экспериментальных данных.
Рис. 12.3. Нахождение энергии активации из графика зависимости k =/(1/7)
Энергетическая диаграмма реакции. Изобразим изменения энергии Е в системе
вдоль некоторой траектории, которую назовем путем реакции Я. Полученная кривая носит название энергетической диаграммы реакции (рис. 12.4).
Рис. 12.4. Энергетическая диаграмма реакции:
Е — средняя энергия теплового движения реагентов при условиях протекания реакции, Ег — энергия, необходимая для преодоления тех сил отталкивания, которые возникают между частицами на близких расстояниях, ЕА — энергия активации, Е] и Е2 — энергия продуктов реакции при значениях теплового эффекта Я, и Н2 соответственно
Видео:Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать
Энергия активации. Уравнение Аррениуса. Теория активных соударений. Катализаторы и их влияние на скорость протекания реакции.
Теоретическая часть
Кинетика – это раздел химии, который занимается изучением закономерностей протекания химических реакций во времени.
Рисунок 1. Гомогенная кинетика и гетерогенная кинетика.
Кинетика имеет два подраздела: гомогенна кинетика и гетерогенная кинетика. Выше приведена схема (рис. 1), объясняющая разницу между ними.
Реакция, изучаемая в данной работе, является гомогенной и, следовательно, рассматриваться будет с точки зрения гомогенной кинетики.
В химической кинетике определяющей величиной является скорость химической реакции. Математически она определяется как отношение изменения концентрации ко времени:
где 
– средняя (1) или мгновенная (2) скорость химической реакции, 
– изменение концентрации исходного вещества (берётся со знаком минус, так как концентрация уменьшается, а скорость не может быть величиной отрицательной) или продукта реакции (берётся со знаком плюс), 
– изменение времени, 
– приращение концентрации, 
– приращении времени.
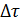
Скорость реакции зависит от:
1) Природы реагирующих веществ;
4) наличия катализаторов (ускоряют реакцию);
5) наличия ингибиторов (замедляют реакцию).
Также можно ввести понятие кинетического уравнение скорости:
Для реакции вида 
можно записать кинетическое уравнение скоростей прямой и обратной реакций:
где 
– константа скорости прямой реакции, 
– константа скорости обратной реакции, 
– концентрации соответствующих веществ, стоящих в степенях, которые называются частными порядками реакции и определяются эмпирически. Сумма частных порядков реакции называется порядком реакции.
Порядок реакции может отличаться от её молекулярности — числа молекул, участвующих в элементарном акте химического превращения.
Константа скорости k – это скорость реакции при единичных концентрациях, она зависит от:
1) Температуры T;
2) Наличия катализаторов/ингибиторов;
3) Природы участвующих в реакции веществ.
Реакции делятся на реакции первого и второго порядка.
К реакциям первого порядка относятся реакции разложения и радиоактивного распада. Общий вид реакций первого порядка:
где T – температура, V – объём.
Для реакций первого порядка можно записать кинетическое уравнение скорости:
И сопоставить его с уравнением (2):
где 
– начальная концентрация исходного вещества.
Можно определить, чему равно отношение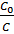 
, введя величину начального количества реагирующего вещества a и количества исходного вещества, которое уже прореагировало 
:
где 
– количество исходного вещества в данный момент времени.
Общий вид реакций второго порядка:
Для таких реакций кинетическое уравнение будет иметь вид, представленный в уравнении (3). Если концентрации исходных веществ равны, можно записать:
где 
– концентрация одного из исходных веществ.
Далее можно вывести формулу зависимости скорости реакции от количества прореагировавших веществ:
Таким образом, зная начальное количество реагирующих веществ и определив прореагировавшее количество в известный момент времени, можно определить константу скорости реакции, на чём и основана методика данного эксперимента.
Энергия активации. Уравнение Аррениуса. Теория активных соударений. Катализаторы и их влияние на скорость протекания реакции.
Как было сказано выше, константа скорости зависит от температуры, наличия катализаторов или ингибиторов и природы реагирующих веществ.
Зависимость константы скорости от температуры определяется уравнением Аррениуса, которое в дифференциальной форме имеет вид:
где 
– константа скорости, 
– температура (в кельвинах), 
– универсальная газовая постоянная, 
– энергия активации.
В данной работе исследуется изменение константы скорости при наличии катализатора, а температура постоянна.
Катализаторами называют вещества, способные ускорять химическую реакцию, при этом сами катализаторы в химической реакции не расходуются. Установлено, что катализаторы изменяют механизм химической реакции. При этом возникают другие, новые переходные состояния, характеризуемые меньшей высотой энергетического барьера. Таким образом, под действием катализатора снижается энергия активации процесса (рис. 2,3).
Для того, чтобы произошла реакция, частицам необходимо преодолеть отталкивание электронных оболочек молекул и разорвать или ослабить связи между атомами. Для этого необходимо затратить определённую энергию.
Избыточная энергия (по сравнению со средней энергией при данной температуре), которой должны обладать молекулы для протекания реакции, называется энергией активации.
Молекулы, обладающие такой энергией, называются активными молекулами.
Все молекулы в веществе находятся в состоянии непрерывного хаотического движения, в результате чего происходят столкновения между молекулами и обмен энергией.
Скорость химической реакции будет зависеть от доли активных молекул.
В ходе реакции молекулы вещества переходят в неустойчивое промежуточное состояние, характеризующееся большим запасом энергии. Именно для его образования необходима энергия активации (рис. 2, 3).
Переходное состояние системы (активированный комплекс) — называется состояние системы реагирующих веществ, соответствующее максимальной энергии на пути реакции.
Энергия активации – это количество дополнительной энергии, необходимой для перехода системы из исходного состояния в состояние активированного комплекса.
Катализаторы направляют реакцию по другому пути, вследствие чего происходит изменение энергии активации.
Все реакции можно поделить на простые и сложные. Простые реакции протекают в одну стадию, а сложные – в несколько. Скорость сложной реакции определяется по самой медленной (лимитирующей) стадии.
Реакции с катализаторами – всегда сложные.
Можно записать влияние катализатора на путь протекания реакции второго порядка:
1. стадия 
2. стадия 
Катализатор подбирается таким образом, чтобы он образовывал с исходными веществами переходный комплекс ABK, а лимитирующей стадией для реакции второго порядка была стадия 2.
Эквивалент.
Эквивалент – реальная или условная частица вещества, которая может замещать, присоединять, высвобождать или быть каким-либо другим способом эквивалентна одному иону водорода в кислотно-основных реакциях, одному электрону в окислительно-восстановительных реакциях или единице заряда в обменных реакциях между солями.
Эксперимент и методика.
Будет проведено две серии экспериментов, которые будут проходить в одних и тех же условиях и отличаться наличием или отсутствием катализатора (Cu2SO4) в составе реакционной смеси. Будут вычислены константы скорости для каждого случая и изменение энергии активации. В данном эксперименте будет исследоваться реакция окисления йодида натрия персульфатом натрия, протекающей в водном растворе по механизму реакции второго порядка.
Количество вещества будет определяться в моль-эквивалентах. Количество моль-эквивалентов иодида аммония и персульфата натрия будет браться одинаковым.
Это количество будет известно заранее.
Так же в раствор будет добавлен тиосульфат натрия, который будет реагировать с получающимся в ходе реакции (I) йодом с образованием иодида аммония:
Таким образом, количество участвующего в реакции (I) иодида аммония будет восстанавливаться до тех пор, пока в растворе не будет полностью израсходован запас тиосульфат натрия, количество которого будет так же определено заранее.
Этот момент можно определить, введя в раствор несколько капель крахмала. В процессе реакции (II) йод постоянно расходуется, однако, когда запас тиосульфата натрия будет израсходован, выделяющийся йод начнёт реагировать с крахмалом, придавая раствору синею окраску. Его количество в этот момент, и прореагировавшее количество одного из исходных веществ, будет равно начальной концентрации добавленного в раствор тиосульфата натрия. Этот момент будет зафиксирован на секундомере.
Таким образом, станут известны три искомые величины, необходимые для определения константы скорости: начальное количество исходных веществ, количество исходных веществ к определённому моменту времени, и само время.
По этим данным будет построен график, значение углового коэффициента которого и будет экспериментально определённым значением константы скорости исследуемой реакции.
Определённая таким образом константа скорости будет относиться только к заданной величине объёма реакционной смеси. Умножив эту константу на объём, находят константу скорости, не зависящую от объёма:
В эксперименте будут использоваться пять колб с засечками, по которым можно определить объём смешанной в них реакционной смеси, мерная колба, мерный стакан, пипетка, секундомер и сосуды с реагентами.
Используемые реагенты находятся в растворах, их нормальные концентрации нанесены на сосуды, в которых они хранятся.
Для расчёта количества эквивалентов реагентов, присутствующих в используемом объёме растворов, используются следующие формулы:
где V – объём данного реагента, измеренный мерной колбой, 
– нормальная концентрация этого реагента. Множитель 1/1000 здесь появляется из-за того, что объём реагента будет измеряться в миллилитрах, а нормальная концентрация измеряется в моль-эквивалентах на литр.
Расчёт изменения энергии активации:
Решение уравнения Аррениуса (15):
Для эксперимента важно, чтобы общий объём реакционной смеси был постоянен и составлял 150 мл.
Таблица с расчётом объёмов растворов реагентов, необходимых для проведения эксперимента приведена ниже.
📺 Видео
Порядок реакции и энергия активацииСкачать
Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать
ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать
Лекция 8: уравнение Аррениуса (30.10.2019)Скачать
Энергия активации химической реакцииСкачать
Уравнение Аррениуса, часть 1Скачать
Скорость химических реакций. 9 класс.Скачать
Скорость реакции. Химия – ПростоСкачать
Введение в кинетикуСкачать
Химическая кинетика. Скорость химической реакции | ХимияСкачать
Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать
Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать
Лекция 18.11.20 | Гетерогенный катализ (завершение), уравнение Аррениуса | Химическая кинетикаСкачать
Лекция 9: теория активных столкновений (06.11.2019)Скачать
Химия для дома. Передача 8. Практическое использование уравнения АррениусаСкачать
Кинетика || Лекция 20 || Теория переходного состояния, уравнение Эйринга, истинная энергия активацииСкачать
С.Аррениус. Определение кислоты как вещества (видео 1) | Кислоты и Основания | ХимияСкачать
Коробов М. В. - Физическая химия II - Основные положения теории активированного комплексаСкачать
