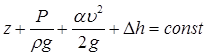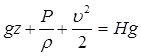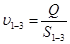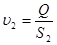Энергетический смысл уравнения бернулли и входящих в него слагаемых (4 видео)

Содержание

Энергетический смысл уравнения Бернулли
Уравнение Бернулли и его практическое применение
Энергетический смысл уравнения Бернулли
Лекция 4
4.2. Геометрическая интерпретация уравнения Бернулли
4.3. Энергетическая интерпретация уравнения Бернулли
4.4. Уравнение Бернулли для потока реальной жидкости
💥 Видео

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Энергетический смысл уравнения Бернулли

Определения

Элементарная струйка – струйка жидкости, боковая поверхность которой образована линией тока, проходящей через бесконечно малый замкнутый контур. Распределение скоростей по поперечному сечению элементарной струйки считается равномерным, по причине малости площади поперечного сечения, поэтому коэффициент Кориолиса 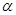равен единице.

Идеальная жидкость – модель жидкости, применяемая для расчётов реальных гидродинамических процессов.

Для идеальной жидкости приняты следующие допущения:

· отсутствуют касательные напряжения между слоями жидкости, следовательно,

отсутствует вязкость жидкости, следовательно, отсутствует трение между слоями жидкости, следовательно, в жидкости отсутствуют потери напора;

· жидкость является не сжимаемой;

· в жидкости отсутствует теплопроводность, т.е. жидкость не изменяет свой объём при изменении температуры;

· поток жидкости является сплошным, т.е. в жидкости отсутствуют места пустот или переуплотнений.

Виды уравнения Бернулли

Для элементарной струйки идеальной жидкости

Для элементарной струйки коэффициент Кориолиса равен единице, в идеальной жидкости отсутствуют потери, поэтому уравнение Бернулли будет иметь вид:

(1)

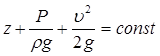
Для потока реальной жидкости

Для потока жидкости коэффициент Кориолиса будет иметь значение отличное от единицы, и зависеть от режима течения, для ламинарного режима α = 2, для турбулентного режима α = 1,05-1,1. Реальная жидкость имеет вязкость, следовательно, в реальной жидкости будут потери напора, поэтому уравнение Бернулли будет иметь вид:

Геометрический смысл уравнения Бернулли

Рассмотрим уравнение Бернулли для элементарной струйки идеальной жидкости (1).

В уравнении (1) все три слагаемых имеют линейную размерность [м]. Соответственно каждую высоту можно представить в виде реальных отрезков:

геометрическая высота, представляет собой расстояние от оси элементарной струйки (трубопровода) до поверхности земли.

пьезометрическая высота, показывает на какую высоту, может подняться жидкость под действием избыточного давления в данной точке, при условии, что на свободную поверхность действует давление внешней газообразной среды (т.е. атмосферное давление).

скоростная высота, показывает высоту, при падении с которой, частица жидкости достигла бы скорости .

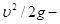
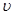
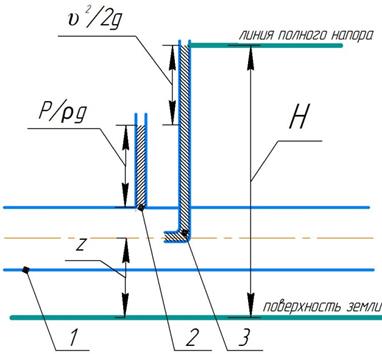
Рис. 1 Иллюстрация геометрического смысла уравнения Бернулли.

1 – элементарная струйка; 2 – пьезометр; 3 – трубка Пито (прибор для измерения скоростной высоты).

Геометрический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх слагаемых уравнения Бернулли остаётся величиной постоянной и равной величине полного напора Н [м].

(2)

Энергетический смысл уравнения Бернулли

Умножим каждое слагаемое уравнения (2) на величину ускорения свободного падения:

В итоге получаем слагаемые, который можно описать с точки зрения энергии:

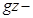
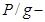
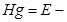
где удельная потенциальная энергия положения, т.е. если поднять жидкость массой 1 кг на высоту , то она будет иметь потенциальную энергию ;

удельная потенциальная энергия давления;

удельная кинетическая энергия;

полная удельная механическая энергия элементарной струйки.

Энергетический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх удельных энергий остаётся величиной постоянной и равной величине полной удельной механической энергии Е [Дж]. Возможна и другая формулировка: уравнение Бернулли – это есть закон сохранения энергии для элементарной струйки (потока) жидкости, который отображает взаимный переход кинетической и потенциальной энергии.

Потери

В потоке реальной жидкости в уравнение Бернулли добавляется слагаемое 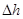, которое

представляет собой величину потерь напора. Запишем уравнение Бернулли для двух произвольных сечений потока жидкости:

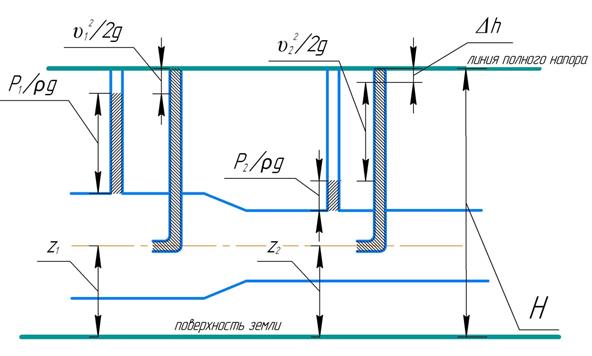
С геометрической точки зрения потери отображаются отрезком, расположенным над скоростным напором, при этом потери отображаются во втором сечении.

Рис. 2. Иллюстрация потерь напора.

С энергетической точки зрения 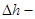это величина, показывающая, сколько энергии жидкость тратит на преодоление различных сопротивлений при переходе из первого сечения во второе сечение.

6. Порядок проведения расчётов:

1. Определить величину расхода жидкости:

2. Поскольку диаметры d₁=d₃, дальнейшие расчёты для широких частей трубопровода будут одинаковы. Поэтому будем проводить расчёт для одной широкой части трубопровода, при этом параметры жидкости, обозначая через индекс _1-3

Определить площади поперечного сечения трубопроводов S_1-3, S₂ [м];

3. Определить скорость течения жидкости:

4. Определить режим течения жидкости:

5. Определить величины скоростного напора: ;

6. На листе А4 построить график, зависимости изменения пьезометрического напора от

длины сечения трубопровода.По оси Х откладываются расстояния между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см

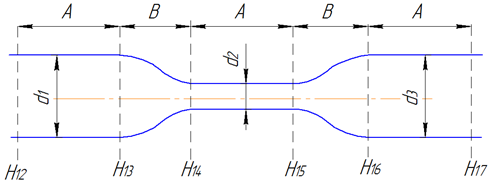
Рис. 3 Условное изображение исследуемого

трубопровода с точками подключения пьезометров.

По оси Y откладываются показания соответствующих пьезометров. В результате получится шесть точек, который соединяются ломаной линией. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

7. На листе А4 построить график, зависимость изменения скоростного напора от длины

сечения трубопровода.По оси Х откладывается расстояние между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см.

По оси Y откладываются значения скоростного напора. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.

8. Вывод о работе с описанием графиков

Таблица 1. Результаты опыта

Видео:Закон БернуллиСкачать

Уравнение Бернулли и его практическое применение

Видео:Закон БернуллиСкачать

Энергетический смысл уравнения Бернулли

Жидкость независимо от того, находится ли она в состоянии покоя или движения, обладает некоторым запасом энергии, равным сумме внутренней, потенциальной и кинетической энергий.

Внутренняя энергия жидкости U представляет собой энергию молекул жидкости, всегда совершающих поступательное и вращательное движения и потому обладающих энергией этих движений.

Рис. 2.10. К определению потенциальной энергии жидкости: 1 — груз; 2 — поршень

Скорость молекул, а следовательно, их внутренняя энергия U увеличивается с повышением температуры. К внутренней энергии относятся также: потенциальная энергия молекул, зависящая от сил притяжения между ними; энергия внутримолекулярных колебаний, которая определяется колебательным движением атомов, входящих в состав молекулы. Внутренняя энергия U измеряется в джоулях (Дж).

Потенциальная энергия жидкости состоит из потенциальной энергии давления и потенциальной энергии положения П_п01 жидкости. Выражение для потенциальной энергии давления можно получить, определив давление поршня на некоторый объем жидкости в сосуде (рис. 2.10).

Если поршень находится под действием груза Р, то жидкость находится под давлением

где F — площадь поршня.

Потенциальная энергия давления в данном случае равна потенциальной энергии груза Ph. Заменяя РнаpFи учитывая, что Fh = V(объем жидкости), получаем, что потенциальная энергия давления

Потенциальная энергия положения П_п01 определяется высотой z центра тяжести (ЦТ) объема жидкости над некоторой произвольно выбранной горизонтальной плоскостью О— О, называемой плоскостью сравнения. Потенциальная энергия положения

где (?_ж — вес жидкости в объеме V

Кинетическая энергия жидкости Т, движущейся со скоростью v, определяется по следующей формуле:

В итоге полная энергия Е жидкости равна Х( U + П^ + П_пол + + Т)

Сумма внутренней энергии и потенциальной энергии давления называется энтальпией (теплосодержанием):

Тогда полная энергия жидкости, Дж,

Разделив все члены выражения (2.15) на т, получим удельную энергию жидкости, Дж/кг, т. е. энергию 1 кг жидкости:

или

где и — внутренняя энергия 1 кг жидкости, Дж/кг; К_об — объем, занимаемый 1 кг жидкости (удельный объем), м 3 /кг; / — удельная энтальпия, т. е. энтальпия 1 кг жидкости, Дж/кг; v — средняя скорость движения жидкости, м/с.

При движении жидкости по трубопроводу без дополнительного подвода энергии (источника работы или тепловой энергии Q) или ее отвода удельная энергия жидкости по закону сохранения энергии не изменяется. При перемещении жидкости

Рис. 2.11. К выводу уравнения Бернулли

от некоторого сечения 1—1 до сечения 2—2 (рис. 2.11) удельные энергии жидкости в этих сечениях будут одинаковы:

Учитывая, что V_o6 = 1/р, (где р — плотность жидкости; К_об — удельный объем жидкости), получаем

Формула (2.18) пригодна для любой жидкости, включая газы и капельные жидкости. Для любой капельной жидкости (идеальной и реальной) р, = р₂ = р. Идеальная жидкость движется без трения, поэтому (при отсутствии подвода теплоты) ее температура и внутренняя энергия и не будут изменяться, следовательно, в данном случае = и₂ = и. Тогда уравнение энергетического баланса (2.18) примет следующий вид:

или

Уравнение (2.19) выражает энергетический баланс движущейся идеальной жидкости и называется уравнением Бернулли. В уравнении (2.19) первый член г,- выражает удельную потенциальную энергию положения жидкости в сечении потока, имеет размерность длины и называется геометрическим напором. Второй член Р

— выражает удельную потенциальную энергию давления жидко- Рg

сти и также имеет размерность длины:

Энергия давления может быть измерена при помощи вертикальной пьезометрической трубки. Под действием давления /?,

жидкость поднимается в трубке на высоту /г. = —, которая назы-

вается пьезометрическим (или статическим) напором. Третий член

уравнения — выражает удельную кинетическую энергию движу- 2 g

щейся жидкости в /-м сечении. Этот член называется скоростным или динамическим напором и также имеет размерность длины:

Скоростной напор равен высоте, на которую может подняться струя жидкости, вытекающей вертикально вверх с начальной скоростью V.

Таким образом, согласно уравнению Бернулли, при движении идеальной жидкости сумма геометрического, пьезометрического и скоростного напоров во всех сечениях потока является постоянной величиной.

Рассмотрим уравнение Бернулли для реальной (вязкой) жидкости (см. рис. 2.13). Реальная жидкость движется с трением. В этом случае при переходе жидкости от сечения 1—1 к сечению 2—2 часть удельной энергии будет расходоваться на преодоление трения и других сопротивлений. Потерянная при этом энергия превращается в теплоту, вследствие чего увеличивается внутренняя энергия жидкости (при отсутствии теплообмена с окружающей средой).

Из уравнений (2.18) и (2.19) (при pj = р₂ = р) получаем

Для реальной жидкости уравнение Бернулли читается так: при установившемся движении реальной жидкости сумма геометрического, пьезометрического, скоростного и потерянного напоров в каждой точке любого сечения потока является постоянной величиной.

Видео:Уравнение Бернулли гидравликаСкачать

Лекция 4

4.1. Уравнение Бернулли для жидкости

Рассмотрим поток жидкости, проходящий по трубопроводу переменного сечения (рис. 10). В первом сечении гидродинамический напор пусть равен H1. По ходу движения потока часть напора H1 необратимо потеряется из-за проявления сил внутреннего трения жидкости и во втором сечении напор уменьшится до H2 на величину потерь напора H.

Уравнение Бeрнýлли для жидкости в самом простейшем виде записывается так:

то есть это уравнение для двух сечений потока в направлении его течения, выраженное через гидродинамические напоры и отражающее закон сохранения энергии (часть энергии переходит в потери) при движении жидкости.

Уравнение Бeрнýлли в традиционной записи получим, если в последнем равенстве раскроем значения гидродинамических напоров H1 и H2 (м) :

Энергетический смысл уравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+hp, кинетической v2/2g энергии и энергии потерь H остаётся неизменной во всех точках потока.

4.2. Геометрическая интерпретация уравнения Бернулли

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

· Как и в гидростатике, величину Z называют нивелирной высотой.

· Второе слагаемое — носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

· Сумма первых двух членов уравнения ¾ гидростатический напор.

· Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

· Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Энергетический смысл уравнения бернулли и входящих в него слагаемых

Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.

4.3. Энергетическая интерпретация уравнения Бернулли

Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.

С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

Физический смысл слагаемых, входящих в уравнение следующий:

· Z — потенциальная энергия единицы веса жидкости (удельная энергия) – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;

· — потенциальная энергия единицы веса жидкости — энергия, обусловленная степенью сжатия единицы веса жидкости, находящейся под давлением ;

· — полная потенциальная энергия единицы веса жидкости;

· — кинетическая энергия единицы веса жидкости — энергия, обусловленная движением единицы веса жидкости со скоростью u;

· H — полная энергия единицы веса жидкости (полная удельная энергия).

4.4. Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т. е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:

где H1-1— напор в первом сечении потока жидкости,

H2-2 — напор во втором сечении потока,

∆h — потерянный напор — энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

4.5. Разность напоров и потери напора

Различие в применении терминов «разность напоров» и «потери напора» с одним и тем же обозначениемH поясним на примерах.

Движение жидкости происходит только при наличии разности напоров (H = H1 — H2), от точки с бóльшим напором H1 к точке с меньшим H2. Например, если два бака, заполненных водой до разных высотных отметок, соединить трубопроводом, то по нему начнётся перетекание в бак с меньшей отметкой уровня воды под влиянием разности напоров H, равной в этом случае разности отметок уровней воды в баках. При выравнивании уровней напоры в обоих баках становятся одинаковыми H1 = H2 , разность напоров H=0 и перетекание прекращается.

Потери напора H отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (H = = 0), однако разность уровней воды будет создавать некоторую разность напоров H. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках H = H1 — H2 , то есть мы опять пришли к уравнению Бернулли.

Таким образом, «разность напоров» является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.

Обычно в гидравлических задачах при известных v или q определяемая величина H назывется потерей напора и, наоборот, при определении v или q известная H — разностью напоров.

4.6. Связь давления и скорости в потоке

Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту закономерность объясним на основе уравнения Бернýлли.

Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по нагнетательному трубопроводу 1 поток рабочей жидкости имеет относительно небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:

Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь напора DH» 0 пренебрегаем. Так как в правой части уравнения кинетическая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отрицательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опустится ниже отметки самой струи (см. рис 11).

Таким образом в струе рабочей жидкости после соплá образуется область пониженного давления или даже вакуум, что вызывает подсос транспортируемой жидкости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отводящему трубопроводу 5.

Водоструйные насосы не имеют трущихся частей, в этом их преимущество перед механическими. По их принципу работают также эжекторы, гидроэлеваторы, насосы для создания вакуума.