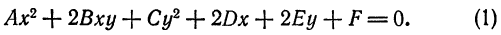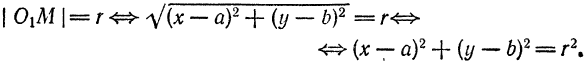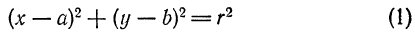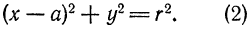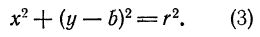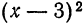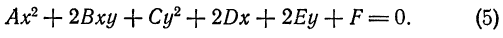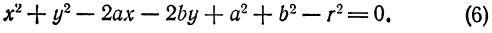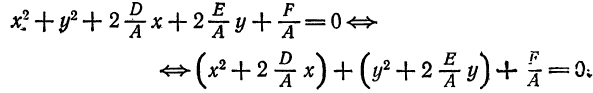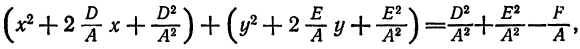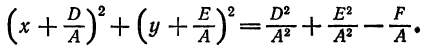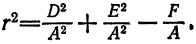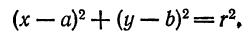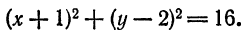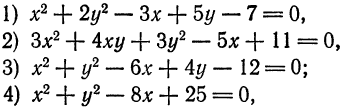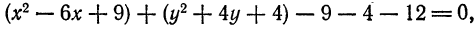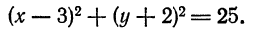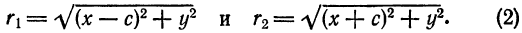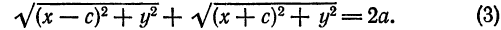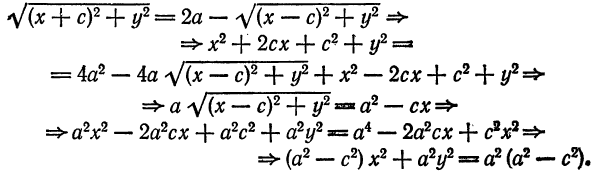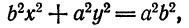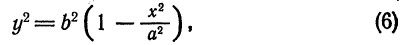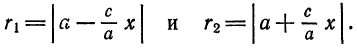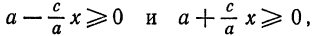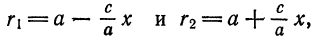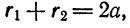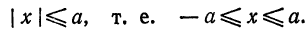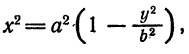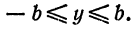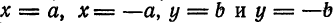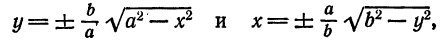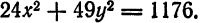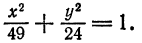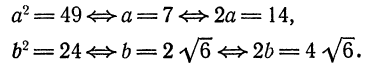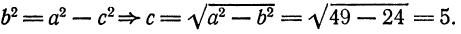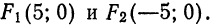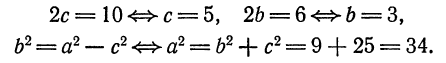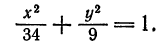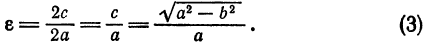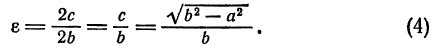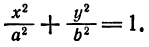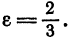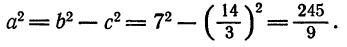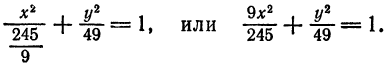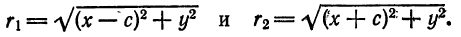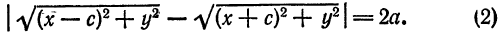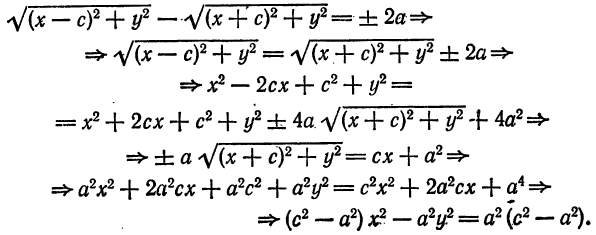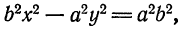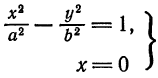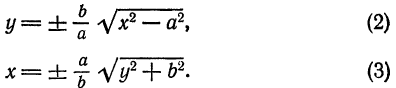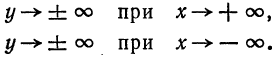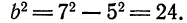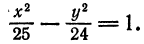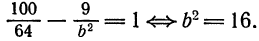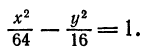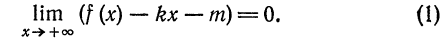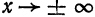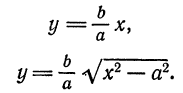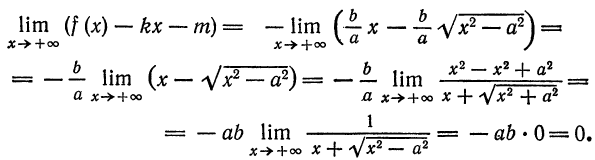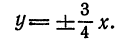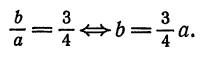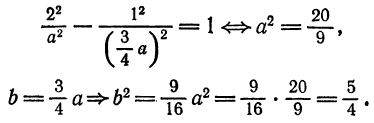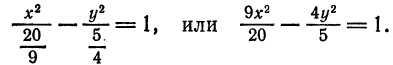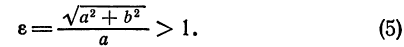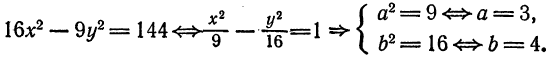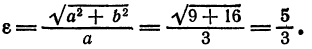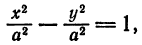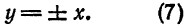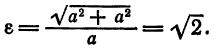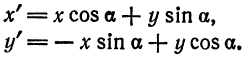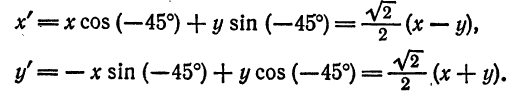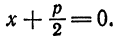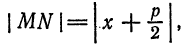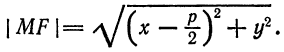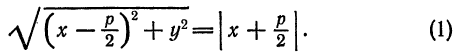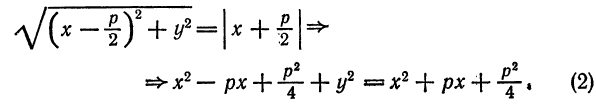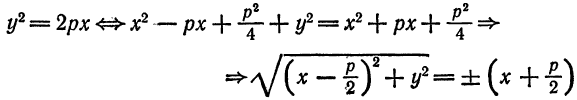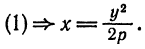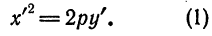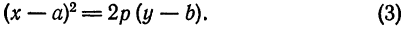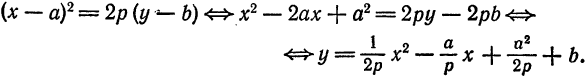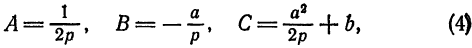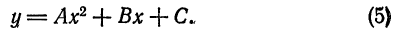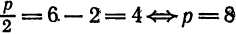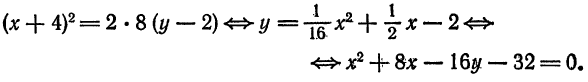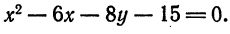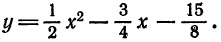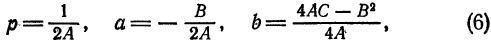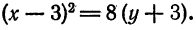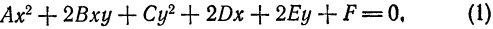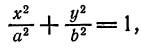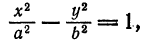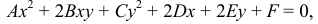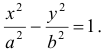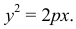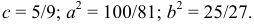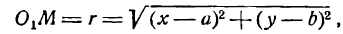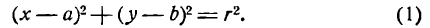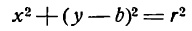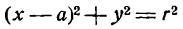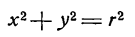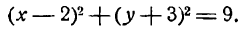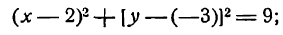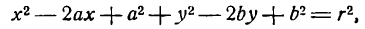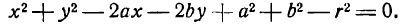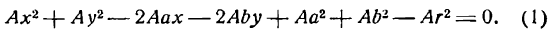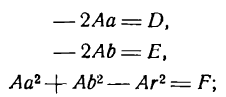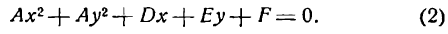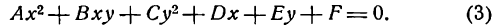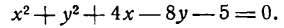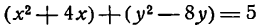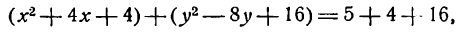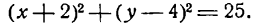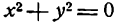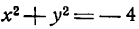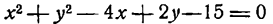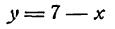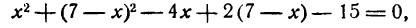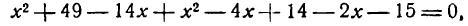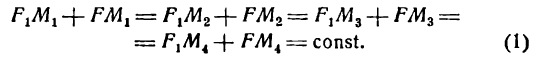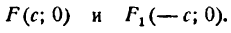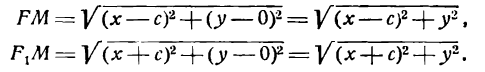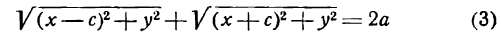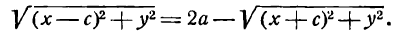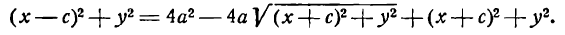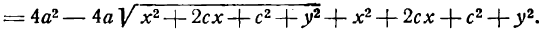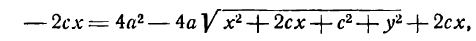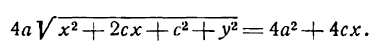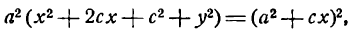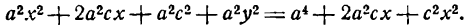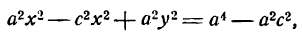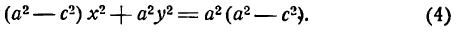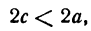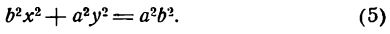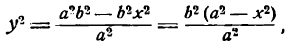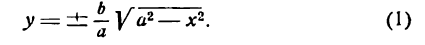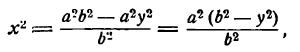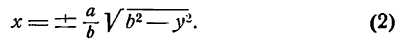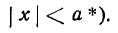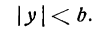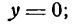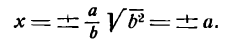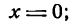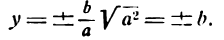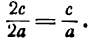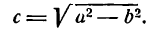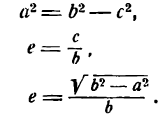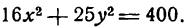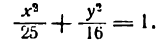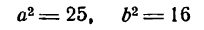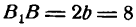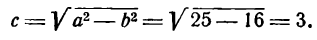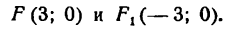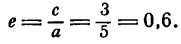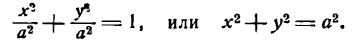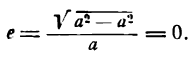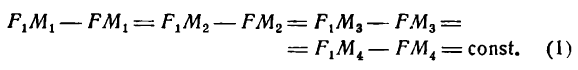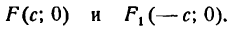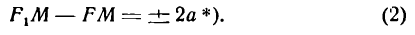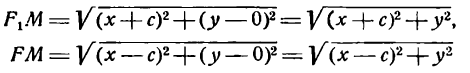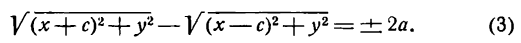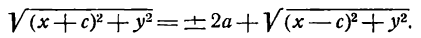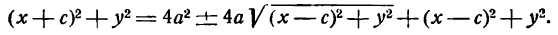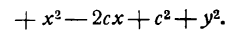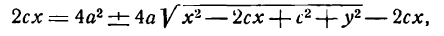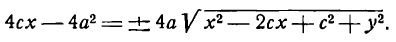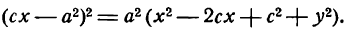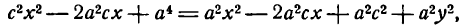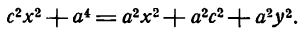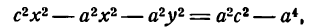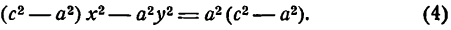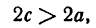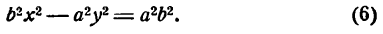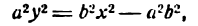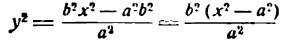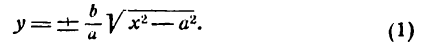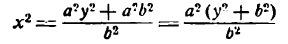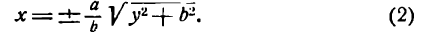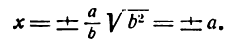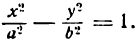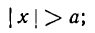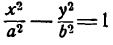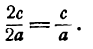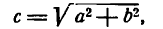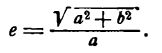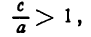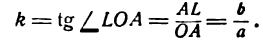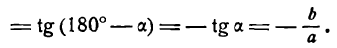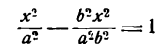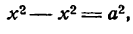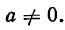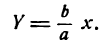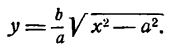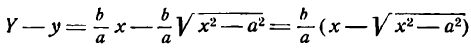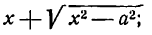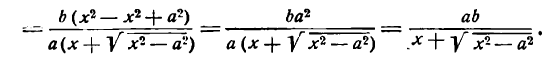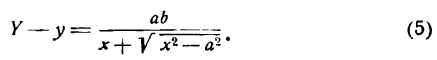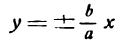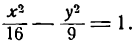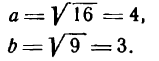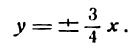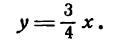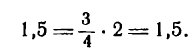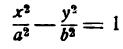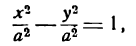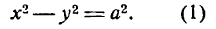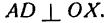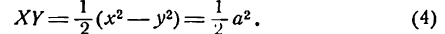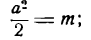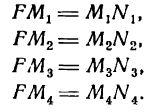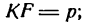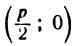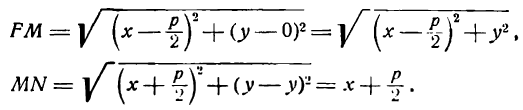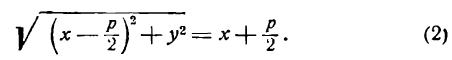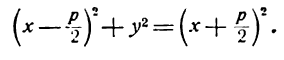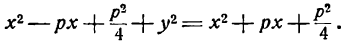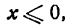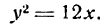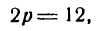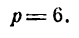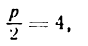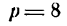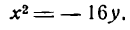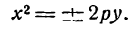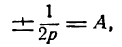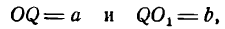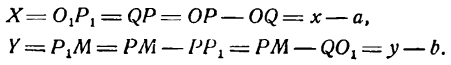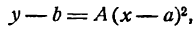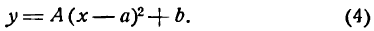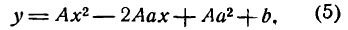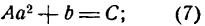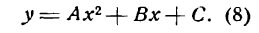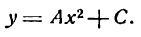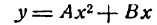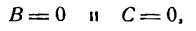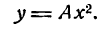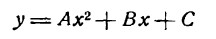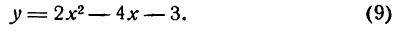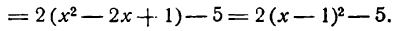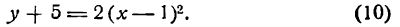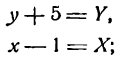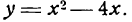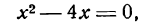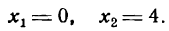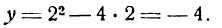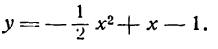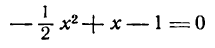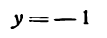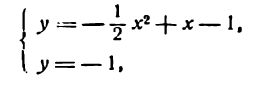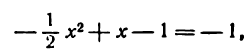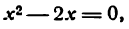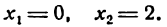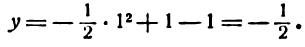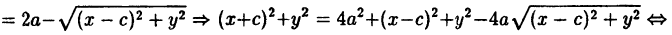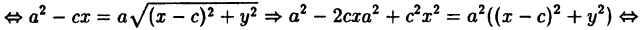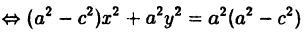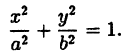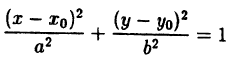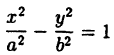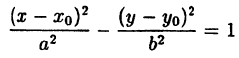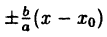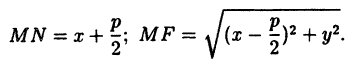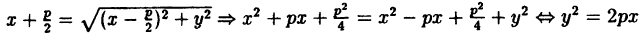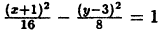- Определение эллипса.
- Фокусы, эксценриситет и директрисы эллипса.
- Уравнение касательной к эллипсу.
- Кривые второго порядка — определение и построение с примерами решения
- Эллипс
- Гипербола
- Кривые второго порядка на плоскости
- Кривые второго порядка в математике с примерами решения и образцами выполнения
- Окружность и ее уравнения
- Эллипс и его каноническое уравнение
- Исследование формы эллипса по его уравнению
- Другие сведения об эллипсе
- Гипербола и ее каноническое уравнение
- Исследование формы гиперболы по ее уравнению
- Другие сведения о гиперболе
- Асимптоты гиперболы
- Эксцентриситет гиперболы
- Равносторонняя гипербола
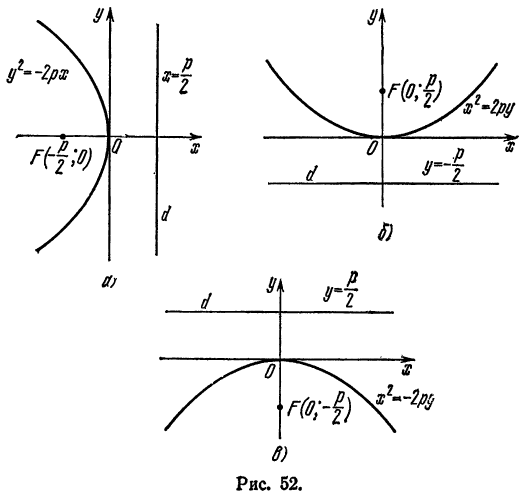
- Парабола и ее каноническое уравнение
- Исследование формы параболы по ее уравнению
- Параллельный перенос параболы
- Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными
- Дополнение к кривым второго порядка
- Эллипс
- Гипербола
- Парабола
- Пример задачи решаемой с применением кривых второго порядка
- Кривая второго порядка и её определение
- Окружность и ее уравнение
- Уравнение окружности как частный вид общего уравнения второй степени
- Эллипс и его уравнение
- Исследование уравнения эллипса
- Эксцентриситет эллипса
- Связь эллипса с окружностью
- Гипербола и ее уравнение
- Исследование уравнения гиперболы
- Эксцентриситет гиперболы
- Асимптоты гиперболы
- Равносторонняя гипербола
- Уравнение равносторонней гиперболы, отнесенной к асимптотам
- Парабола и ее простейшее уравнение
- Исследование уравнения параболы
- Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
- Конические сечения
- Кривая второго порядка и её вычисление
- Уравнение линии в декартовых и полярных координатах
- Окружность
- Эллипс
- Гипербола
- Парабола
- Понятие о приведении общего уравнения второго порядка к каноническому виду
- Решение заданий на тему: Кривые второго порядка
- 🎦 Видео
Видео:§28 Эксцентриситет эллипсаСкачать

Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>+frac<y^><b^>=1label
$$
при условии (a geq b > 0).
Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
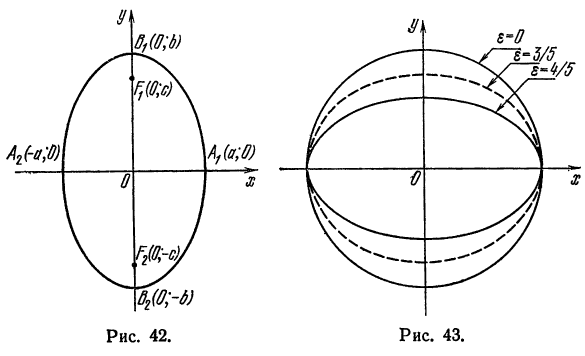
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
Рис. 8.1. Эллипс
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_), (M_) и (M_) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^+y^=a^). При каждом (x) таком, что (|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
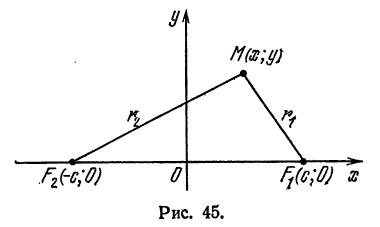
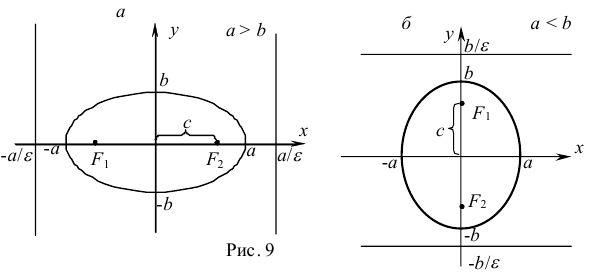
Фокусами называются точки (F_) и (F_) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что (varepsilon Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_=|F_M|=a-varepsilon x, r_=|F_M|=a+varepsilon x.label
$$
Очевидно, что (r_^=(x-c)^+y^). Подставим сюда выражение для (y^), найденное из уравнения эллипса. Мы получим
$$
r_^=x^-2cx+c^+b^-frac<b^x^><a^>.nonumber
$$
Учитывая равенство eqref, это можно преобразовать к виду
$$
r_^=a^-2cx+frac<c^x^><a^>=(a-varepsilon x)^.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.
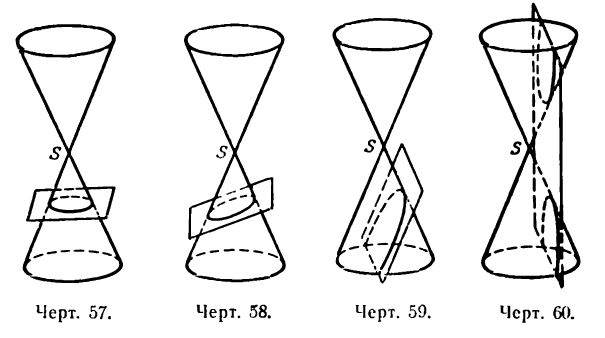
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_+r_=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^+y^>=2a-sqrt<(x+c)^+y^>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=asqrt<(x+c)^+y^>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^x^+a^y^=a^b^), равносильному уравнению эллипса eqref.
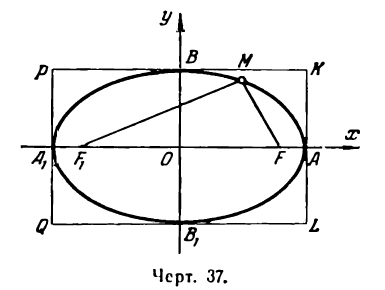
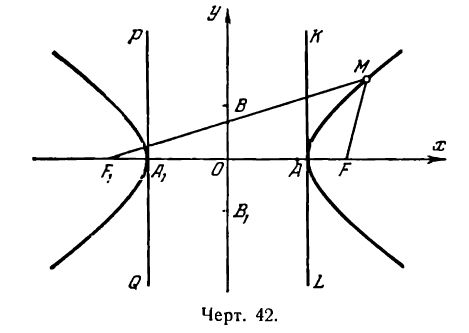
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Видео:§18 Каноническое уравнение эллипсаСкачать

Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_(x_, y_)) — точка на эллипсе и (y_ neq 0). Через (M_) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ > 0) это график (f_(x)=bsqrt<1-x^/a^>), для (y_ Утверждение 5.
Касательная к эллипсу в точке (M_(x_, y_)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Видео:ЭллипсСкачать

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
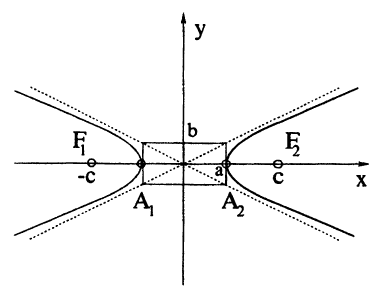
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

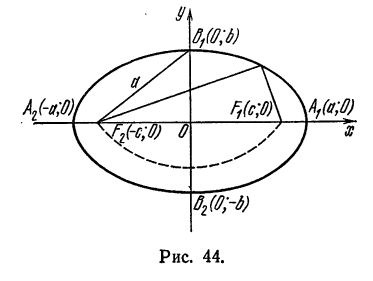
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

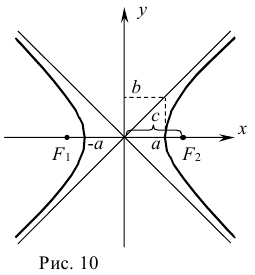
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Кривые второго порядка в математике с примерами решения и образцами выполнения
1) всякая прямая в прямоугольной системе координат 
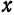
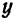
2) всякое уравнение первой степени 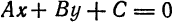
Мы займемся изучением линий, определяемых уравнениями второй степени относительно текущих
координат 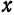
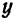
Такие линии называются линиями (кривыми) второго порядка. Коэффициенты уравнения (1) могут принимать различные действительные значения, исключая одновременное равенство 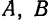
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Окружность и ее уравнения
Как известно, Окружностью называется множество всех точек плоскости, одинаково удаленных от данной точки, называемой центром.
Пусть дана окружность радиуса 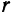
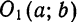
Возьмем на данной окружности произвольную точку
(рис. 38). Имеем
удовлетворяют координаты произвольной точки окружности. Более того, этому уравнению не удовлетворяют координаты никакой точки, не лежащей на окружности, так как 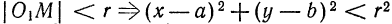
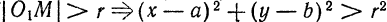
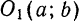
Если центр окружности находится на оси 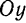
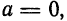
Наконец, если центр окружности находится в начале координат, т. е. если 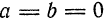
Пример:
Составить уравнение окружности радиуса 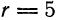
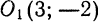
Решение:
Имеем: 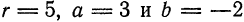
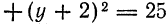
Из изложенного выше следует, что уравнение окружности является уравнением второй степени относительно переменных 
переменными
В самом деле, раскрыв скобки в уравнении (1), получим
Справедливо следующее утверждение: если в уравнении (5) 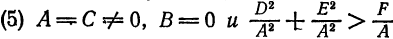
Действительно, разделив уравнение (5) почленно на 
Дополним группы членов, стоящие в скобках, до полного квадрата:
Положим 
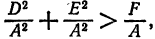
Получим
Если в уравнении 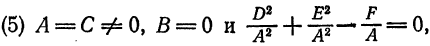
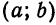
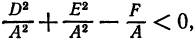
Пример:
Найти координаты центра и радиус окружности
Решение:
Сравнивая данное уравнение с уравнением (1), находим: 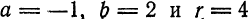
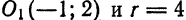
Пример:
Установить, какое из уравнений:
определяет окружность. Найти координаты центра и радиус каждой из них.
Решение:
Первое уравнение не определяет окружность, потому что 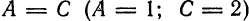
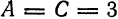
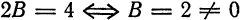
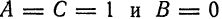
Это уравнение, а следовательно, и уравнение 3), определяет окружность с центром 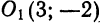
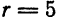
В четвертом уравнении также выполняются условия 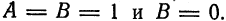
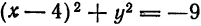
Эллипс и его каноническое уравнение
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
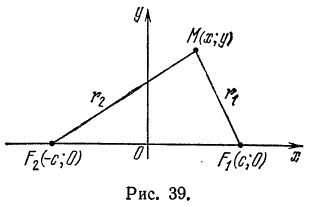
Составим уравнение эллипса, фокусы 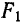
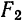
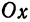
начала координат (рис. 39).
Обозначив 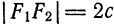
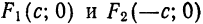
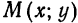
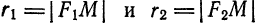
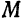
тогда, согласно определению эллипса, 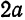
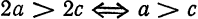
Подставив найденные значения 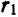
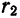
Преобразуем уравнение (3) следующим образом!
Имеем: 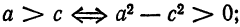
последнее уравнение примет вид
Так как координаты 
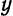
Покажем, что справедливо и обратное: если координаты точки 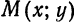
Пусть 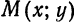
то 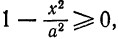
Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим
Но так как 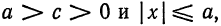
т. е. точка 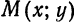
Уравнение (5) называется каноническим уравнением
эллипса.
Исследование формы эллипса по его уравнению
Определим форму эллипса по его каноническому
уравнению
1. Координаты точки 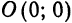
Найдем точки пересечения эллипса с осями координат. Положив в уравнении (1) 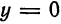
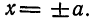
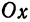
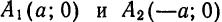
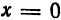
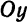
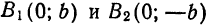
3. Так как в уравнение (1) переменные 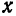
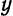
4. Определим область изменения переменных 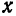
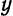
Аналогично, переписав уравнение эллипса (1) в виде
получим 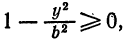
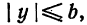
Таким образом, все точки эллипса находятся внутри прямоугольника, ограниченного прямыми
(см. рис, 40).
5. Переписав уравнение (1) соответственно в вида
мы видим, что при возрастании 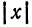
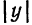
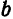
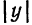
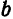
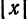
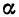
Точки 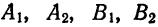
называются вершинами эллипса. Отрезок 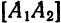
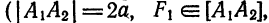
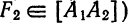
большой осью эллипса, а отрезок 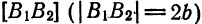
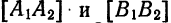
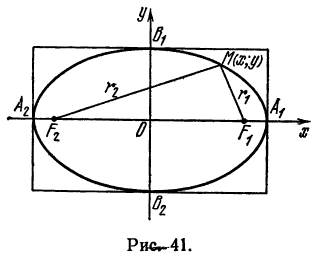
Пример:
Определить длину осей и координаты фокусов эллипса
Решение:
Разделив обе части данного уравнения на 1176, приведем его к каноническому виду
Следовательно,
Пример:
Составить каноническое уравнение эллипса, если фокусное расстояние равно 10, а малая ось равна 6.
Решение:
Другие сведения об эллипсе
Мы рассмотрели эллипс, у которого 

определяет эллипс, фокусы которого лежат на оси 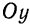
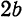
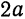
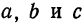
Определение:
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси и обозначается буквой 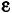
Если 
При 
Из формул (3) и (4) следует 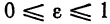
увеличением разности между полуосями 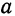
эллипса, приближаясь к единице; при уменьшении разности между 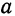
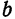
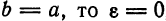
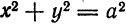
Из рис. 43, на котором изображены эллипсы 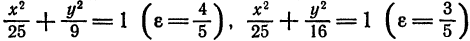
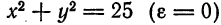
Для этого на осях координат строим вершины эллипса 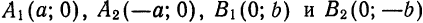
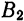
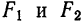
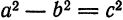
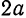
острием карандаша и описываем кривую, оставляя нить все время в натянутом состоянии.
Пример:
Составить каноническое уравнение эллипса, фокусы которого лежат на оси 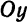
Решение. Так как фокусы лежат на оси 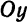
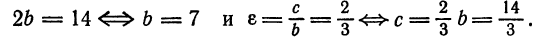
формуле (2) находим:
Следовательно, искомое уравнение, будет
Видео:Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

Гипербола и ее каноническое уравнение
Определение:
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Составим уравнение гиперболы, фокусы которой 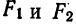
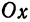
Обозначив 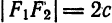
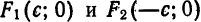
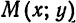
Расстояния 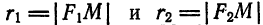
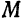
где 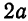
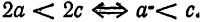
в равенство (1), получим уравнение гиперболы
Уравнение (2) можно привести к более простому виду; для этого преобразуем его следующим образом:
Имеем: 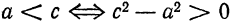
тогда последнее равенство принимает вид
Так как координаты 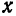
Как и в случае эллипса (см. конец § 2), можно показать, что справедливо и обратное: если координаты точки 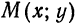
Уравнение (4) называется каноническим уравнением гиперболы.
Исследование формы гиперболы по ее уравнению
Определим форму гиперболы по ее каноническому уравнению
1. Координаты точки 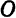
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (1) 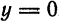
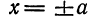
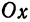

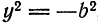
не имеет действительных решений. Следовательно, гипербола не пересекает ось 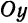
3. Так как в уравнение (1) переменные 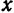
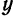
4. Определим область изменения переменных 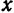
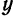
Имеем: 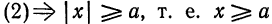
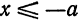
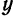
5. Из (2) следует также, что
Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой 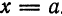
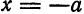
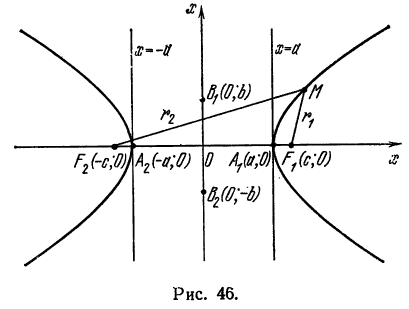
Гипербола имеет форму, изображенную на рис. 46.
Точки 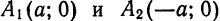
соединяющий вершины гиперболы, называется действительной осью. Отрезок 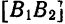
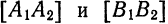
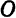
Пример:
Составить уравнение гиперболы, вершины которой находятся в точках 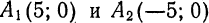
Решение:
Имеем: 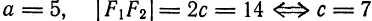
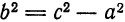
Следовательно, искомое уравнение будет
Пример:
Составить каноническое уравнение гиперболы с фокусами на оси 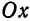
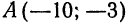
Решение:
Имеем: 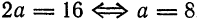
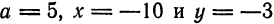
Другие сведения о гиперболе
Асимптоты гиперболы
Определение:
Прямая 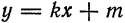
асимптотой кривой 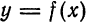
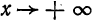
Аналогично определяется асимптота при 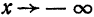
являются асимптотами гиперболы
при
Так как прямые (2) и гипербола (3) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 47). Напишем уравнения прямых (2) и гиперболы (3), соответствую*
щие первой четверти:
Положив 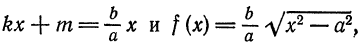
Следовательно, прямые (2) являются асимптотами гиперболы (3).
Отметим, что асимптоты (2) совпадают с диагоналям прямоугольника, стороны которого параллельны осям 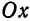
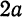
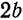
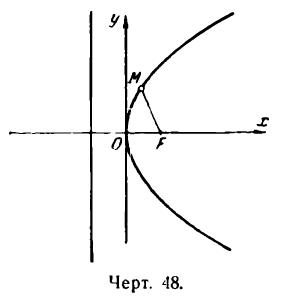
образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис.48).
Пример:
Составить уравнение гиперболы, проходящей через точку 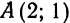
Решение:
Из данных уравнений асимптот имеем:
Заменив в уравнении гиперболы переменные 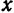
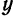
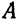
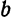
Следовательно, искомое уравнение будет
Эксцентриситет гиперболы
Определение:
Эксцентриситетом гиперболы называется отношение расстояния между фокусами
к длине действительной оси и обозначается буквой 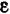
Из формулы 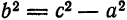
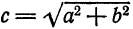
Пример:
Найти эксцентриситет гиперболы 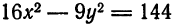
Решение:
По формуле (5) находим
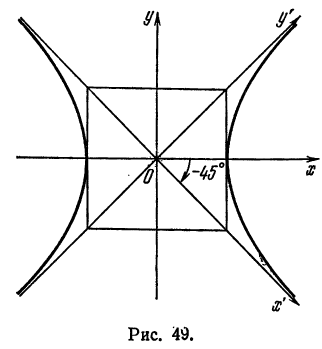
Равносторонняя гипербола
Гипербола называется равносторонней, если длины ее полуосей равны между собой, т. е. 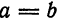
Равносторонняя гипербола определяется одним пара*
метром 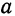
У всех равносторонних гипербол один и тот же эксцентриситет:
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат 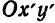
Составим уравнение равносторонней гиперболы относительно новой системы координат 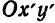
(4) § 3 гл. 2:
Положив 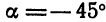
Учитывая равенство (6), получим
Уравнение (8) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.
Из уравнения (8) следует, что переменные 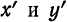
Пример:
Составить каноническое уравнение
равносторонней гиперболы, проходящей через точку 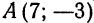
Решение:
Заменив в уравнении (6) переменные 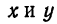
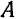
Следовательно, искомое уравнение будет
Видео:§17 Определение эллипсаСкачать

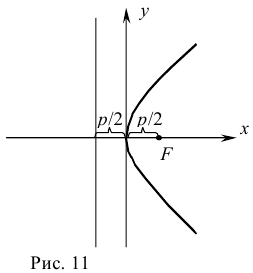
Парабола и ее каноническое уравнение
Определение:
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, не проходящей через данную точку и
называемой директрисой.
Составим уравнение параболы, фокус 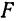
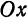
директриса 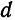
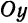
Расстояние от фокуса 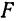
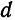
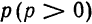
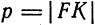
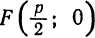
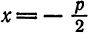
Пусть 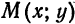
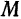
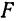
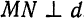
а по формуле расстояния между двумя точками
согласно определению параболы
Уравнение (1) является искомым уравнением параболы. Для упрощения уравнения (1) преобразуем его следующим образом:
Последнее уравнение эквивалентно
Координаты 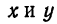
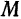
Покажем, что справедливо и обратное: если координаты точки 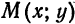
Но так как из (3) 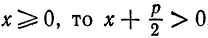
Уравнение (3) называется каноническим уравнением параболы.
Исследование формы параболы по ее уравнению
Определим форму параболы по ее каноническому уравнению
1. Координаты точки 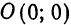
2. Так как в уравнение (1) переменная 
Так как 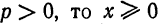
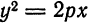
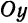
4. При возрастании абсциссы 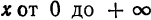
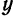
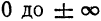
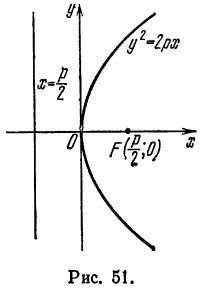
Парабола 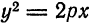
Ось 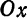
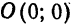
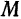
5. Если фокус параболы лежит слева от оси 
Координаты ее фокуса будут 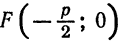
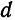
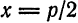
6. Если фокус параболы имеет координаты 
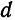

7. Наконец, если фокус параболы имеет координаты 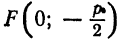
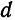
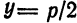
Пример:
Дана парабола 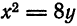
Решение:
Данная парабола симметрична относительно оси 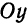
Следовательно, фокус имеет координаты 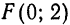
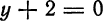
Пример:
Составить уравнение параболы с вершиной в начале координат, директриса которой задана уравнением 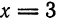
Решение:
Из условия задачи следует, что парабола симметрична относительно оси 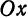
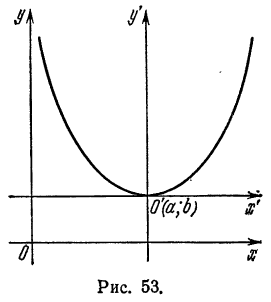
Параллельный перенос параболы
Пусть дана парабола с вершиной в точке 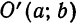
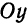
Требуется составить ее уравнение. Сделаем параллельный перенос осей координат, поместив начало в точке 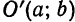
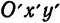
Чтобы получить уравнение данной параболы относительно старой системы, воспользуемся формулами преобразования прямоугольных координат при параллельном переносе;
Подставив значения 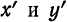
Преобразуем это уравнение следующим образом:
С уравнением параболы вида (5) читатель хорошо знаком по школьному курсу.
Пример 1. Составить уравнение параболы с вершиной в точке 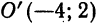
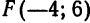
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси 
Заменив в уравнении (3) 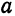
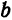
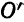
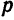
Пример:
Дано уравнение параболы
Привести его к каноническому виду.
Решение:
Разрешив данное уравнение относительно переменной 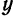
Сравнивая это уравнение с уравнением (5), находим 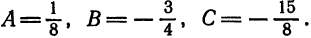
следовательно, 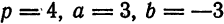
Положив 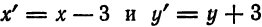
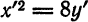
Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными
Выше было установлено, что уравнение окружности есть частный случай общего уравнения второй степени с переменными 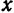
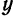
Покажем, что и канонические уравнения эллипса, гиперболы и параболы являются частными случаями уравнения (1). В самом деле:
1) при 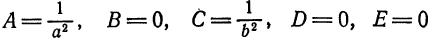
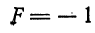
т. е. определяет эллипс;
2) при 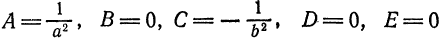
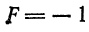
т. е. определяет гиперболу;
3) при 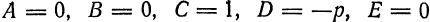

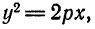
Видео:166. Найти каноническое уравнение эллипса.Скачать

Дополнение к кривым второго порядка
Пусть задана кривая, определяемая уравнением второй степени
где 
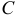
Приведем еще одно определение кривой второго порядка.
Геометрическое место точек плоскости, для которых отношение их расстояний до заданной точки, называемой фокусом, и до заданной прямой, называемой директрисой, есть величина постоянная, равная 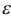
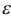
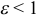
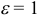
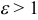
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек 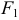
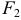
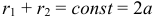
Каноническое уравнение эллипса: 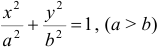
Если 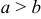
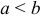
Если 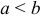
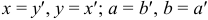
Декартова прямоугольная система координат, в которой уравнение эллипса имеет канонический вид, называется канонической.
Точки пересечения эллипса с осями координат называются вершинами эллипса. Расстояния от начала координат до вершин 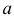
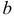
Центр симметрии эллипса, совпадающий с началом координат, называется центром эллипса.
Если 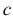
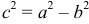
Отношение 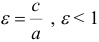
Расстояние от произвольной точки 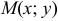
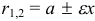
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе имеют вид 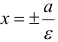
Гипербола
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек 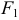
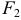
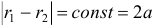
Декартова прямоугольная система координат, в которой уравнение гиперболы имеет канонический вид, называется канонической. Каноническое уравнение гиперболы:
Ось абсцисс канонической системы пересекает гиперболу в точках, называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. 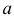
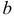
Если 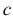
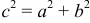
Отношение 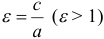
Расстояние от произвольной точки 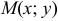
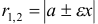
Гипербола с равными полуосями 
Прямые с уравнениями 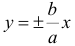
Прямые 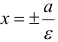
Парабола
Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки 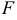
Указанная точка 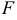
Система координат, в которой парабола имеет канонический вид, называется канонической, а ось 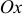
Каноническое уравнение параболы:
Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Фокус параболы 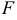
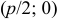
Директрисой параболы называется прямая 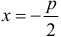
Расстояние от произвольной точки параболы до фокуса 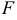
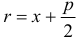
Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Пример задачи решаемой с применением кривых второго порядка
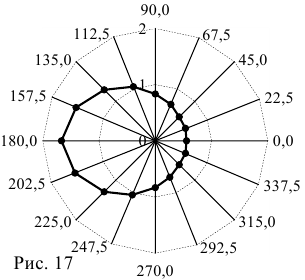
Линия задана уравнением 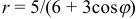
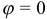
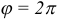
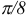
Решение:
1) Вычисляя значения 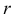
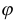
Используя полученные табличные значения, построим кривую в полярной системе координат (рис. 17).
2) Используя формулы перехода
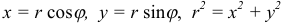
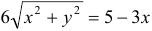
Возведем левую и правую части в квадрат: 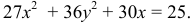
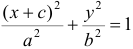
3) Это эллипс, смещенный на 
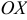
Ответ: эллипс 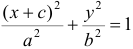
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Видео:Видеоурок "Гипербола"Скачать

Кривая второго порядка и её определение
| Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением |
Окружность и ее уравнение
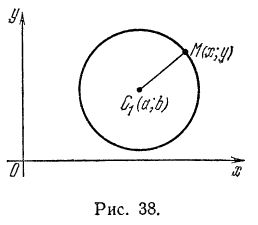
Окружностью называется геометрическое место точек, одинаково удаленных от одной точки, называемой центром.
Пользуясь этим определением, выведем уравнение окружности. Пусть радиус ее равен r, а центр находится в точке
О1(а; b). Возьмем на окружности произвольную точку М(х; у) (рис. 27).
По формуле расстояния между двумя точками можем написать:
или, после возведения обеих частей равенства в квадрат,
Так как точка М нами взята произвольно, а радиус r — величина постоянная, то равенство (1) справедливо для всех точек окружности, т. е. координаты любой ее точки удовлетворяют этому равенству. А если так, то равенство (1) нужно рассматривать как уравнение окружности.
В уравнении (1) а и b — координаты центра окружности, а х и у — текущие координаты.
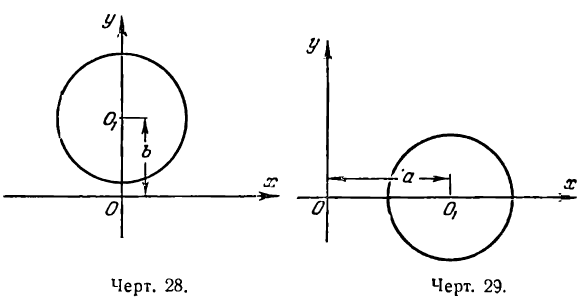
Если положить а = 0, то уравнение (1) обратится в следующее:
и будет определять окружность с центром на оси Оу (рис. 28).
При b = 0 уравнение (1) примет вид
и будет определять окружность с центром на оси Ох (рис. 29).
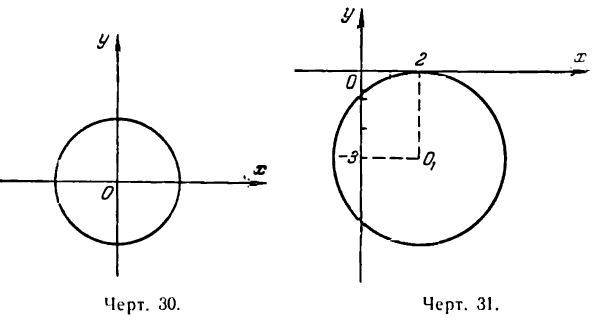
Наконец, при а = 0 и b = 0 уравнение (1) преобразуется в следующее:
и будет определять окружность с центром в начале координат (рис. 30).
Можно построить окружность, имея ее уравнение. Пусть, например, требуется построить окружность
Перепишем это уравнение в следующем виде:
сравнивая это уравнение с(1), видим, что координаты центра окружности суть (2; — 3) и радиус ее r = 3. Построив
точку О1(2;—3), опишем из нее радиусом, равным 3 единицам масштаба, искомую окружность (рис. 31).
Уравнение окружности как частный вид общего уравнения второй степени
Раскрыв скобки в уравнении (1) , можем написать:
Умножив все члены последнего равенства на А, получим:
тогда уравнение (1) окружности примет вид
Уравнение (2) является частным случаем общего уравнения второй степени с двумя переменными. В самом деле, сравним уравнение (2) с общим уравнением второй степени с двумя переменными, имеющим, как известно, следующий вид:
Мы видим, что уравнение (2) отличается от уравнения (3) только тем, что у первого коэффициенты при х2 и у2 одинаковы и отсутствует член, содержащий произведение ху.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нем коэффициенты при х2 и у2 равны между собой и отсутствует член с произведением ху.
Обратно, уравнение вида (2), вообще говоря, определяет окружность. Убедимся в этом на примере. Пусть дано уравнение
Перепишем его в следующем виде:
и преобразуем двучлены, стоящие в скобках, в полные квадраты суммы и разности, прибавив к первому 4, ко второму 16. Чтобы равенство при этом не нарушилось, увеличим и правую часть его на сумму 4+16. Получим:
Последнее равенство является уравнением окружности, имеющей радиус, равный 5, и центр в точке О1(-2; 4).
Бывают однако случаи, когда уравнение (2) при некоторых значениях коэффициентов не определяет окружности; например, уравнению
удовлетворяют координаты единственной точки (0; 0), а уравнению
не удовлетворяют координаты ни одной точки, так как сумма квадратов действительных чисел не может иметь отрицательного значения.
Пример:
и хорда 
Решение:
Так как концы хорды являются общими точками окружности и хорды, то их координаты удовлетворяют как уравнению первой, так и уравнению второй линии. Поэтому, чтобы найти эти координаты, нужно решить совместно уравнения окружности и хорды. Подставив значение
в уравнение окружности, получим:
Находим значение у:
Итак, концами хорды служат точки с координатами (4; 3) и (6; 1).
По формуле расстояния между двумя точками можем определить искомую длину хорды
Эллипс и его уравнение
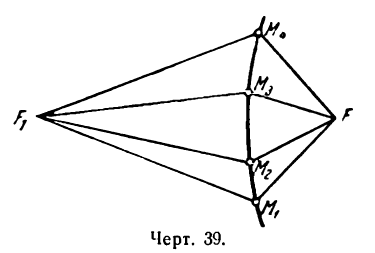
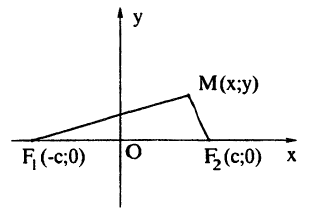
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (и болыиая, чем расстояние между фокусами).
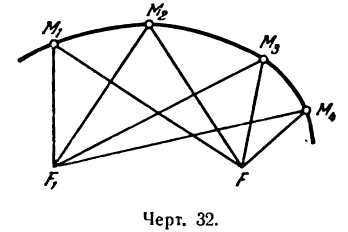
Пусть, например, на эллипсе взяты точки М1, M2, M3, М4 и т. д. (рис. 32). Если фокусы обозначить через F и F1, то согласно данному определению можно написать:
Геометрическое место точек, обладающих вышеуказанным свойствам (1), и есть эллипс.
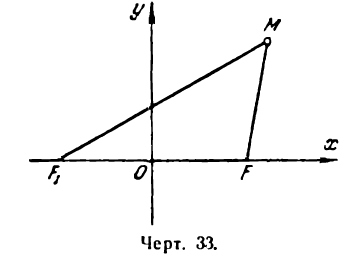
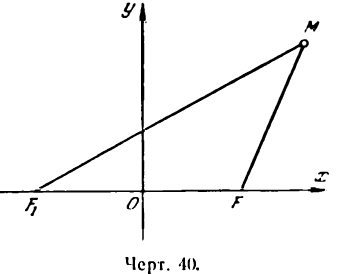
На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ох примем прямую, проходящую через фокусы F и F1, а за ось Оу — прямую перпендикулярную
к FF1 и проведенную через середину отрезка FF1 (рис. 33). Обозначим расстояние F1F между фокусами через 2с, тогда координаты фокусов будут:
Возьмем на эллипсе произвольную точку М(х;у). Обозначим постоянную величину суммы расстояний каждой точки от фокусов через 2а, тогда
По формуле расстояния между двумя точками найдем:
Теперь равенство (2) перепишется следующим образом:
и будет представлять уравнение эллипса в принятой системе координат.
Упростим уравнение (3). Для этого перенесем один из радикалов в правую часть уравнения:
Возведем обе части этого равенства в квадрат:
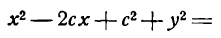
Приведем подобные члены:
Сократив на 4 и снова возведя в квадрат обе части равенства, получим:
Перенесем все члены, содержащие х и у, в левую часть равенства, остальные члены — в правую:
Но согласно определению эллипса
Из последнего неравенства следует, что 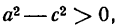
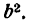
Наконец, разделим все члены последнего равенства на 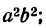
где х и у — текущие координаты точек эллипса, а
Уравнение (6) и есть простейший вид уравнения эллипса *).
*) Уравнение (6) получилось в результате двукратного возведения в квадрат уравнения (3), благодаря чему, вообще говоря, возможно появление посторонних корней. Можно показать, что уравнение (6) не имеет посторонних корней, т. е. любая точка, координаты которой удовлетворяют уравнению (6), лежит на эллипсе.
Исследование уравнения эллипса
Определим сначала у из уравнения (5) :
Из того же уравнения (5) найдем:
Рассмотрим теперь равенства (1) и (2).
I. Пусть
*) | х | означает, что х берется по абсолютной величине; таким образом, запись | х |
Тогда каждому значению у, как мы видим из равенства (2), отвечают два значения х равные по абсолютной величине, но с разными знаками. Отсюда следует, что каждому значению у соответствуют на эллипсе две точки, симметричные относительно оси Оу.
Из сказанного заключаем: эллипс 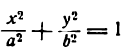
II. Найдем точки пересечения эллипса с осью Ох. Пусть
тогда из равенства (2) имеем:
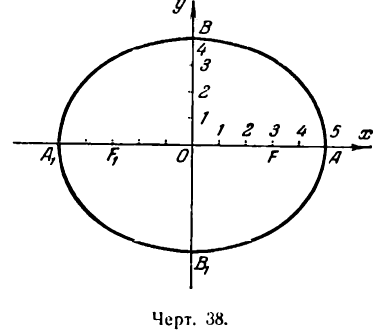
Отсюда следует: эллипс пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (точки А и А1 на рис. 34).
III. Найдем точки пересечения эллипса с осью Оу. Пусть
тогда из равенства (1) имеем:
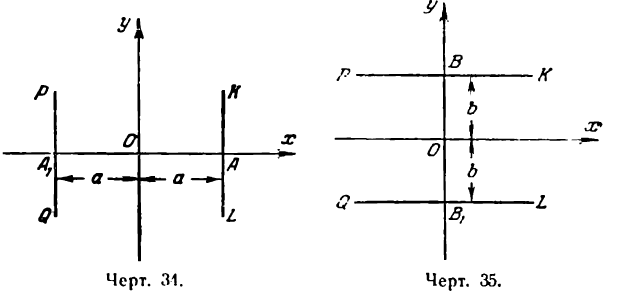
Отсюда заключаем, что эллипс пересекает ось Оу в двух точках, координаты которых (0; b) и (0; —b) (точки В и В1 на рис. 35).
IV. Пусть х принимает такие значения, что
тогда выражение под корнем в равенстве (1) будет отрицательным, и, следовательно, у будет иметь мнимые значения. А это значит, что не существует точек эллипса, абсциссы которых удовлетворяют условию (3), т. е. эллипс расположен внутри полосы, заключенной между прямыми х = + а и х = — а (рис. 34, прямые КL и РQ).
Если же положить
то из равенства (2) получим для х мнимые значения. Это говорит о том, что точки, удовлетворяющие условию (4), на эллипсе не лежат, т. е. эллипс заключен между прямыми у = + b и у = — b (рис. 35, прямые РК и QL .
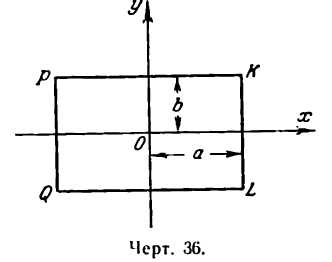
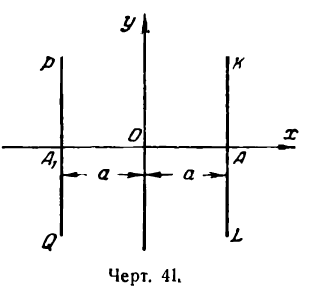
Из сказанного следует, что все точка эллипса лежат внутри прямоугольника, стороны которого параллельны координатным осям и имеют длины, равные 2а и 2b, а диагонали пересекаются в начале координат (рис. 36).
Эллипс имеет форму, показанную на рис. 37, Точки A,, A1, В и В1 называются вершинами эллипса, а точка О — его центром. Отрезок А1А = 2а называется его большой осью, а отрезок В1В = 2b — малой осью, Отрезки FМ и F1М носят название фокальных радиусов точки М.
Эксцентриситет эллипса
Эксцентриситетом эллипса называется отношение расстояния между его фокусами к длине большой оси, т. e.
Эксцентриситет обычно обозначают буквой е. Таким образом,
Но согласно формуле (7)
Поэтому для определения эксцентриситета может служить
Так как 0 а уравнение (6) представляет эллипс, фокусы которого лежат на оси Оу; в этом случае его большая ось равна 2 b , а малая 2 а . В соответствии с этим формула (7) и формулы (1) и (2) настоящей лекции примут такой вид:
Пример:
Определить длину его осей, координаты вершин и фокусов, а также величину эксцентриситета.
Решение:
Разделив обе части данного уравнения на 400, получим:
Итак, большая ось эллипса 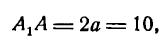
Координаты вершин его будут:
Чтобы найти координаты фокусов, нужно узнать величину
Из равенства (7) имеем:
Следовательно, координаты фокусов будут:
Наконец, по формуле (1) настоящей лекции находим:
Связь эллипса с окружностью
Положим, что полуоси эллипса равны между собой, т. е. а = b, тогда уравнение эллипса примет вид
Полученное уравнение, как известно, определяет окружность радиуса, равного а.
Посмотрим, чему будет равен эксцентриситет в этом случае; полагая в формуле (2)
Отсюда заключаем, что окружность есть частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Гипербола и ее уравнение
Гиперболой называется геометрическое место точек, разность расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная берется по абсолютному значению, причем она меньше расстояния между фокусами и не равна нулю).
Пусть, например, точки М1, М2, M3, М4 лежат на гиперболе, фокусы которой находятся в точках F и F1 (рис. 39). Тогда, согласно данному выше определению, можно написать:
Пользуясь определением гиперболы, выведем ее уравнение.
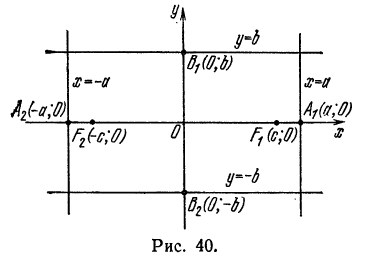
Примем за ось Ох прямую, проходящую через фокусы F и F1 (рис. 40), а за ось Оу — прямую, перпендикулярную к отрезку F1F и делящую его пополам.
Положим F1F = 2c тогда координаты фокусов будут
Возьмем на гиперболе произвольную точку М(х; у) и обозначим величину разности расстояний каждой точки от фокусов через 2а; тогда
По формуле расстояния между двумя точками найдем:
и, заменив в равенстве (2) F1М и FМ их выражениями, напишем:
Это и есть уравнение гиперболы относительно выбранной системы координат, так как оно согласно равенствам (1) справедливо для любой ее точки.
*) Знак + берется в случае, если F1М > FМ , и знак —, если F1М
Возведем обе части уравнения в квадрат:
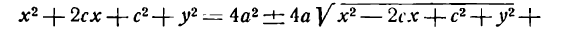
Приведем подобные члены:
Сократив на 4, снова возведем в квадрат обе части уравнения; получим:
Перенесем в левую часть члены, содержащие х и у, а остальные члены в правую:
Согласно определению гиперболы
При условии (5) разность 
Сделав это в равенстве (4), получим:
Разделив последнее равенство на 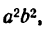
где х и у— текущие координаты точек гиперболы, а
Равенство (7) представляет собой простейший вид уравнения гиперболы *).
*) Как и в случае эллипса, можно показать, что уравнение (7) равносильно уравнению (3), т. е. не имеет посторонних корней.
Исследование уравнения гиперболы
Из уравнения (6) имеем:
Из этого же уравнения (6) находим:
Исследуем уравнения (1) и (2) для выяснения геометрической формы гиперболы.
I. Найдем точки пересечения гиперболы с осью Ох. Для этого полагаем, у = 0 и из уравнения (2) получаем:
Отсюда следует: гипербола пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (рис. 41, точки А и А1).
II. Положим в уравнении (1)
тогда у получит мнимое значение, а это значит, что на гиперболе нет точек, удовлетворяющих условию (3). Следовательно, в полосе между прямыми х = + а и х = — а (прямые KL и РQ на рис. 41) нет точек гиперболы
III. Пусть
тогда из равенства (1) найдем для каждого х два действительных значения у, равных по абсолютной величине, но с противоположными знаками. А это значит, что каждому значению х, удовлетворяющему неравенству (4), соответствуют на нашей кривой две точки, симметричные относительно оси Ох.
Следовательно, гипербола 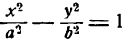
С другой стороны, для каждого значения у из равенства (2) найдем два действительных значения х, равных по абсолютной величине, но противоположных по знаку, т. е. каждому значению у на гиперболе соответствуют две точки, симметричные относительно оси Оу.
Следовательно, гипербола 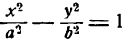
IV. Если в уравнении (1) давать х значения, заключенные между +a и 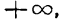
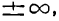
Если же давать х значения, заключенные между — а и 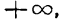
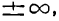
Из всего изложенного следует, что гипербола
состоит из двух симметричных относительно оси Оу бесконечных ветвей, одна из которых расположена справа от
прямой х = + а, а другая слева от прямой х = — а. Каждая из этих ветвей симметрична относительно оси Ох (рис. 42).
Точки А(а; 0) и А1(- а; 0) называются вершинами гиперболы, а точка О (0; 0) — ее центром.
Отрезок АА1 = 2а носит название действительной или вещественной оси гиперболы в отличие от оси ВВ1 = 2b, называемой мнимой *).
*) Отрезок ВВ1 = 2b называется мнимой осью, так как на нем нет точек гиперболы.
Отрезки F1М и FМ — фокальные радиусы точки М.
Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине вещественной оси, т. е.
Эксцентриситет гиперболы, так же как и для эллипса, обозначается буквой е:
Но согласно равенству (8)
поэтому формулу (1) можно представить в следующем виде:
Так как для гиперболы с > а , то дробь
а потому эксцентриситет гиперболы больше единицы.
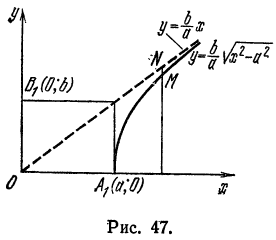
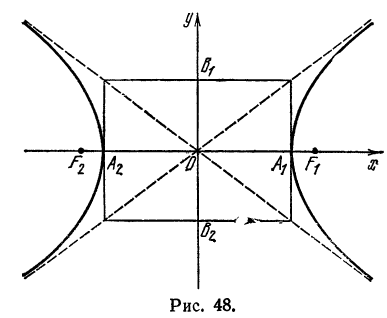
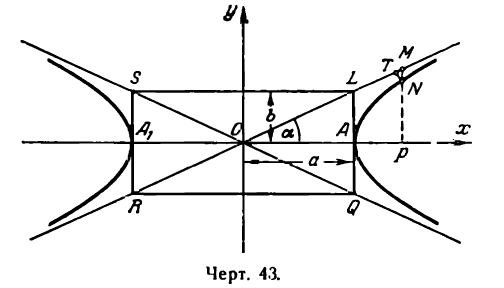
Асимптоты гиперболы
Построим на осях гиперболы
прямоугольник LQRS со сторонами, равными 2а и 2b и проведем его диагонали LR и QS продолжив их по обе стороны (рис. 43).
Прямая LR проходит через начало координат, поэтому ее уравнение будет:
Но угловой коэффициент
Заменив в уравнении (1) 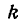
Прямая QS также определяется уравнением (1), но угловой коэффициент ее будет уже другой, а именно:
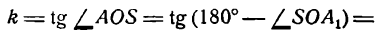
Таким образом, уравнение прямой QS будет:
Обычно уравнения (2) и (3) записывают следующим образом:
Между прямыми, представленными уравнениями (4), и гиперболой существует связь; выясним ее.
Решим совместно способом подстановки уравнения (4) и
уравнение гиперболы
что невозможно, так как
Таким образом, прямые (4) х2 уа
и гипербола 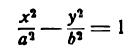
Возьмем на прямой LR и на гиперболе точки М и N, расположенные в первом координатном углу и имеющие одну и ту же абсциссу. Ординатой точки М служит РМ; обозначим ее через Y в отличие от ординаты точки N которую обозначим буквой у. Из уравнения (2) можно написать:
Из уравнения гиперболы имеем:
и посмотрим, как она будет изменяться при возрастании абсциссы. Для этого умножим и разделим правую часть последнего равенства на выражение
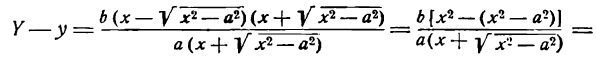
Пусть величина х в равенстве (5) бесконечно возрастает, тогда знаменатель дроби также бесконечно растет, а сама дробь уменьшается, приближаясь к нулю. Таким образом, гипотенуза NМ и, следовательно, катет NT в прямоугольном треугольнике МNТ стремится к нулю. Из сказанного делаем вывод: при неограниченном возрастании абсциссы х гипербола приближается к прямой LR как угодно близко, нигде ее не пересекая.
Так как прямые LR и QS, а также точки гиперболы симметричны относительно оси Ох, то можно сказать, что и часть гиперболы, расположенная в четвертом координатном углу, как угодно близко подходит к прямой QS , нигде ее не пересекая.
Вывод, сделанный для правой ветви гиперболы, справедлив и для ее левой ветви благодаря той же симметричности прямых (4) и гиперболы относительно координатных осей.
называются асимптотами гиперболы.
Из сказанного в настоящей лекции можно сделать заключение, что гипербола расположена всеми своими точками внутри вертикальных углов, образуемых асимптотами, и нигде не выходит за их границы. Этим обстоятельством можно воспользоваться для построения гиперболы в случае, если не требуется точного, а достаточно только приближенного ее изображения; для этого, нарисив асимптоты, нужно провести плавную кривую линию, постепенно приближая ее к асимптотам.
Пример:
Дана гипербола
Узнать, лежит ли точка A(2; 1,5) на какой-либо ее асимптоте.
Решение:
Из данного уравнения имеем:
Следовательно, уравнения асимптот будут:
Так как точка А лежит согласно условию в первом координатном углу, то она может принадлежать только асимптоте, определяемой уравнением
Подставив в него вместо х и у координаты точки А, получим тождество:
Значит, точка А лежит на указанной асимптоте гиперболы.
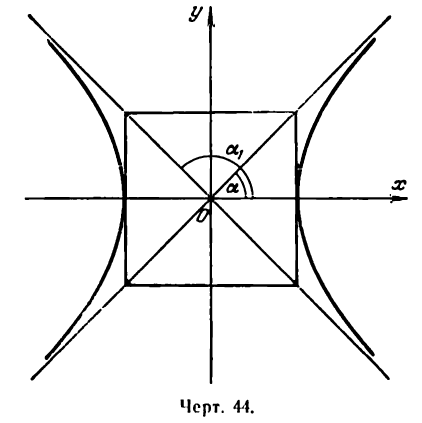
Равносторонняя гипербола
Если в уравнении гиперболы
положим а = b то это уравнение примет вид
Уравнение (1) определяет гиперболу, у которой полуоси равны между собой. Такая гипербола называется равносторонней. Уравнения асимптот в этом случае будут:
так как отношение
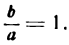
Как видно из уравнения (2), угловые коэффициенты асимптот равны + 1 и —1 . Если обозначить углы, образуемые асимптотами с положительным направлением оси Ох, соответственно через а и а1 (рис. 44), то
Следовательно, угол между асимптотами будет:
Отсюда заключаем: асимптоты равносторонней гиперболы взаимно перпендикулярны.
Уравнение равносторонней гиперболы, отнесенной к асимптотам
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, то их можно принять за оси прямоугольной системы координат и рассматривать гиперболу по отношению к этим новым осям. Выведем уравнение равносторонней гиперболы для этого случая.
Пусть дана равносторонняя гипербола. Тогда ее уравнение по отношению к координатным осям Ох и Оу (рис. 45)
выразится, как было пока-* у зано в , в виде
Взяв на гиперболе произвольную точку М (х; у) и построив ее координаты, будем иметь:
Примем теперь за оси координат асимптоты гиперболы: ОХ— за ось абсцисс, ОY — за ось ординат. Опустив перпендикуляр МС на новую ось абсцисс, найдем:
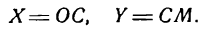
Выразим новые координаты X н Y точки М через старые х и у. Для этого из точки А проведем 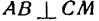
Обратим внимание на то, что в образовавшихся прямоугольных треугольниках АМВ и АОD
как углы, образованные взаимно перпендикулярными прямыми. Но
Из рисежа имеем:
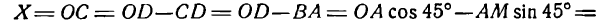
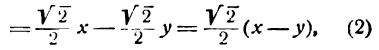
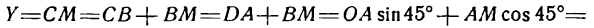
Перемножив равенства (2) и (3) и приняв во внимание равенство (1), получим:
Положим для краткости
тогда равенство (4) перепишется так:
где m— постоянная величина.
Таково уравнение равносторонней гиперболы, если за оси координат принять ее асимптоты.
Как видно из уравнения (5), переменные X и Y — величины обратно пропорциональные, а потому можно сказать, что равносторонняя гипербола ху = m представляет собой график обратно пропорциональной зависимости между переменными величинами.
Парабола и ее простейшее уравнение
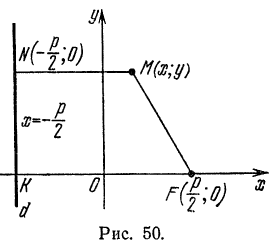
Параболой называется геометрическое место точек, каждая из которых одинаково удалена от точки, называемой фокусом, и от прямой, называемой директрисой <при условии, что фокус не лежит на директрисе).
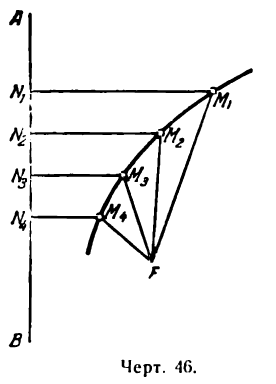
Пусть точки М1 М2, М3, М4 лежат на параболе (рис. 46).
Если точка F изображает фокус, а прямая АВ— директрису, то согласно данному выше определению можем написать:
Выведем уравнение параболы, пользуясь ее определением. Для этого выберем систему координат, приняв за ось Ох прямую, проведенную через точку F (фокус) перпендикулярно к директрисе АВ, а за
ось Оу — прямую, проходящую через середину отрезка КF перпендикулярно к последнему (рис. 47). Обозначим
тогда координаты фокуса F будут
Возьмем на параболе произвольную точку М(x; у) расстояния ее от фокуса F и от директрисы АВ будут выражаться соответственно отрезками FМ и МN. Согласно определению параболы, можем написать:
Применяя формулу расстояния между двумя точками и приняв во внимание, что точка N имеет координаты 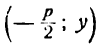
Заменив FМ и МN в равенстве (1) их выражениями, получим:
Это и есть уравнение параболы относительно выбранной системы координат, так как оно справедливо для любой ее точки.
Упростим уравнение (2). Для этого возведем обе части его в квадрат:
Приведя подобные члены, получим простейшее уравнение параболы
*) Можно показать, что уравнение (3) равносильно уравнению (2). Величина р называется параметром параболы.
Исследование уравнения параболы
Из уравнения (3) найдем:
Исследуем уравнение (1) для выяснения геометрической формы нашей кривой, полагая р > 0.
I. Положим
Отсюда следует: парабола 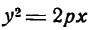
II. Если х 0, то у имеет два действительных значения, равных по абсолютной величине, но с разными знаками. Это значит, что каждому положительному значению х на параболе соответствуют две точки, расположенные симметрично относительно оси Ох.
Следовательно, парабола 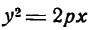
IV. Пусть х неограниченно возрастает, тогда и 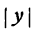
Итак, парабола 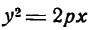
Вышеизложенное позволяет представить параболу, как показано на рис. 48.
Точка О называется вершиной параболы, отрезок FМ — фокальным радиусом точки М параболы, а бесконечная прямая Ох является ее осью симметрии.
Если директрису параболы поместить справа от начала координат, то фокус и ветви ее расположатся как показано на рисеже 49.
При этом абсциссы точек параболы будут удовлетворять условию
а потому ее уравнение примет вид:
Парабола может быть симметрична и относительно оси Оу в этом случае фокус ее будет лежать па оси ординат, а директрисой будет прямая, параллельная оси Ох. Как видно при этом условии координатные оси поменяются ролями, и уравнение параболы примет вид
если ветви ее направлены вверх (рис. 50), и
если ветви направлены вниз (рис. 51).
Пример:
Найти координаты ее фокуса и написать уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси Ох и расположена направо от оси Оу. Из уравнения находим:
Расстояние фокуса от начала координат равно 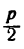
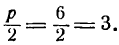
Директрисой служит прямая, параллельная оси Оу и отстоящая от последней на расстоянии 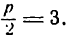
уравнение директрисы параболы будет х = — 3.
Пример:
Фокус параболы с вершиной в начале координат лежит в точке F(0; —4). Написать уравнение этой параболы.
Решение:
Согласно условию данная парабола симметрична относительно оси Оу, а ветви ее направлены вниз, поэтому искомое уравнение найдется из (3). Так как
и уравнение параболы будет:
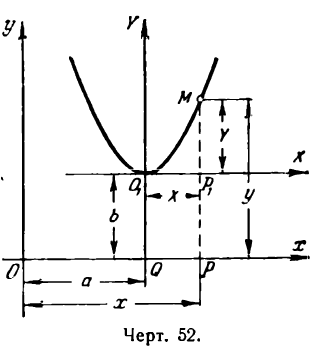
Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
Возьмем уравнения параболы (2) и (3) и запишем их в следующем виде:
Положив в уравнении (1)
Уравнение (2) определяет параболу, ветви которой направлены вверх, если А > О, вниз, если А
Возьмем на параболе произвольную точку М(х; у). Опустив из нее перпендикуляр МР на ось Ох, будем иметь:
Проведем через О1 прямые О1Х и QY, параллельные координатным осям Ох и Оу, и положим временно, что прямые О1Х и О1Y служат осями новой системы координат. Обозначим координаты точки М в этой системе через X и Y, т. е.
Уравнение параболы в новой системе координат напишется следующим образом:
Чтобы найти ее уравнение относительно прежних осей Ох и Оу, нужно X и Y выразить через х и y. Так как
Подставив в уравнение (3) найденные значения X и Y, получим:
Упростим уравнение (4); для этого раскроем в нем скобки.
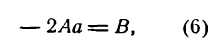
тогда уравнение (5) примет вид
Это—уравнение параболы с вершиной, лежащей в любой точке плоскости, и с осью симметрии, параллельной оси Оу.
Рассмотрим частные случаи.
Пусть абсцисса вершины параболы a = 0; тогда величина В в равенстве (6) также будет нулем и уравнение (8) примет следующий вид:
Полученное уравнение определяет параболу, у которой вершина лежит на оси Оу, являющейся в то же время и ее осью симметрии (рис. 53).
Положим, что одна из точек параболы (исключая ее вершину) лежит в начале координат; тогда координаты (0; 0) должны удовлетворять уравнению (8). Заменив в нем х и у нулями, найдем С=0. В этом случае уравнение (8) получит вид
и будет определять параболу, проходящую через начало координат (рис. 54).
Заметим, что и уравнение (2) можно рассматривать как частный случай уравнения (8). Действительно, положив в равенствах (6) и (7)
вследствие чего уравнение (8) преобразуется в следующее:
Из сказанного следует, что парабола, у которой ось симметрии параллельна оси Оу или совпадает с ней, определяется уравнением
при любых значениях А, В и С, кроме А = 0.
Убедимся на примере, что справедливо и обратное утверждение: всякое уравнение вида (8) определяет параболу с осью симметрии, параллельной оси Оу.
Пусть дано уравнение
Преобразуем его следующим образом:
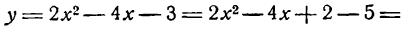
тогда уравнение (10) примет вид:
Уравнение (11) имеет такой же вид, как и уравнение (2), поэтому оно, а следовательно, и уравнение (9) определяют параболу, у которой ось симметрии параллельна оси Оу.
Для построения параболы, определяемой уравнением вида (8), можно использовать обычный прием, применяемый для вычерчивания графиков функций, а именно: дав х ряд значений, вычислить значения у, а затем, построив точки по найденным координатам, провести через них плавную линию.
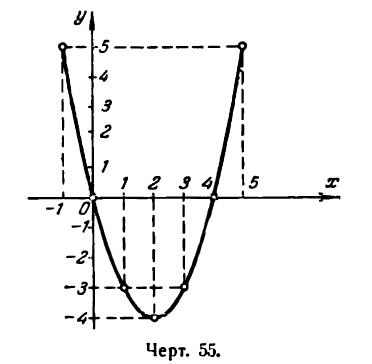
Пример:
Решение:
Прежде всего найдем абсциссы точек пересечения данной параболы с осью Ох; положив у = 0, получим:
Так как найденные точки симметричны относительно оси параболы, то вершина последней, находясь на этой оси, имеет 0 + 4 0
абсциссу, равную 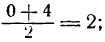
Этих трех точек достаточно для приближенного изображения параболы.
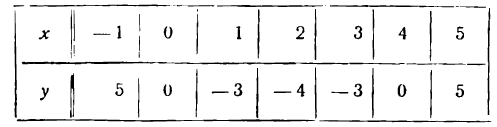
Для более точного ее представления нужны дополнительные точки. Составим следующую таблицу:
Построив эти точки и прозедя через них плавную линию, получим искомую параболу (рис. 55).
Пример:
Решение:
мнимые, а потому ось Ох не пересекает данную параболу. В этом случае следует найти абсциссы точек пересечения параболы с прямой
(-1 — свободный член данного уравнения параболы)
Решая для этой цели систему уравнений
Полученные точки симметричны относительно оси параболы, поэтому абсцисса ее вершины равна 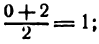
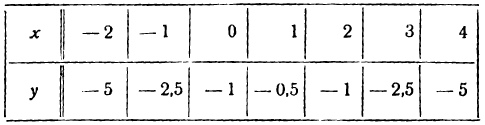
Присоединим к этим точкам несколько дополнительных точек. Составим таблицу:
Конические сечения
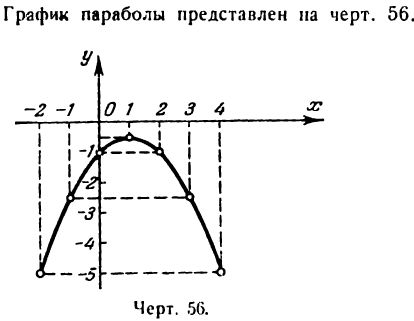
Окружность, эллипс, гипербола и парабола определяются, как мы установили в предыдущих лекциях уравнениями второй степени относительно текущих координат; поэтому их называют кривыми второго порядка. Они были известны еще древним грекам, которые изучали эти кривые, рассматривая их как результат сечения прямого кругового конуса плоскостью в следующих четырех случаях.
I. Секущая плоскость перпендикулярна к оси конуса; в сечении получается окружность (рис. 57).
II. Секущая плоскость образует с осью конуса угол, не равный 90°, и пересекает все его образующие по одну сторону от вершины S; в сечении получается эллипс (рис. 58).
III. Секущая плоскость параллельна какой-либо образующей конуса; при этом получается кривая, называемая параболой (рис. 59).
IV. Секущая плоскость пересекает обе полости конуса; при этом получаются две бесконечные ветви, образующие гиперболу (рис. 60).
Окружность, эллипс, гипербола и парабола называются коническими сечениями.
Конические сечения изучались в древности исключительно геометрическим путем, что представляло большие трудности, и только со времени Декарта, давшего метод координат, изучение их значительно упростилось.
Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Кривая второго порядка и её вычисление
Уравнение линии. Кривые второго порядка. Окружность. Эллипс. Гипербола. Парабола. Приведение к каноническому виду.
Уравнение линии в декартовых и полярных координатах
В лекции 3 было введено понятие неявной функции, задаваемой уравнением вида F(x,y) = 0.
Определение 6.1. Множество точек плоскости, координаты которых удовлетворяют некоторому уравнению
(6.1) F(x;y) = 0
называется линией (плоской кривой).
Не всякое уравнение определяет линию. Например, уравнение x² + y² = -1 не определяет никакой линии. Кроме того, линия может состоять из отдельных точек. Так, например, уравнению x² + y² = 0 удовлетворяет только начало координат.
Линия не обязательно является графиком функции. Так, например, уравнение x² + y² = 1 определяет окружность с центром в начале координат и радиуса 1 (т.к. d = 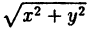
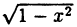
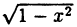
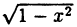
Уравнение произвольной окружности с центром в точке M(a;b) и радиусом R будет иметь вид:
(6.2) (х — а)² + (у- b)² = R²,
т.к. окружность радиусом R есть геометрическое место точек плоскости, находящихся на расстоянии R от центра, т.е. в соответствии с формулой ( 6.2) d = 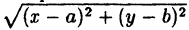
В частности, окружность с центром в начале координат, радиусом R, описывается уравнением
x² + y² = R².
Пример 6.1. Какую линию описывает уравнение x² + y² = Rx?
Решение: Перенося Rx в левую часть и выделяя полный квадрат, получаем:
x² + y² = Rx ⇔ X2 — Rx + у² = 0 ⇔ x² — Rx + 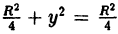
(х — 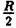
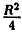
Ответ: данное уравнение описывает окружность с центром в точке M(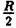
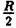
Линия может определяться на плоскости уравнением как в декартовых, так и в полярных координатах: F(




Пример 6.2. Построить график функции, заданной в полярных координатах уравнением r = 2 sin3

Решение: Составим таблицу некоторых значений этой функции:
 | 0 | 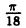 | 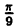 | 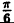 | 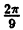 | 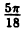 | 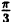 | 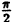 |
| r | 0 | 1 | 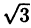 | 2 | 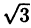 | 1 | 0 | -2 |
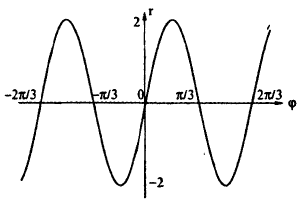

Далее, пользуясь тем, что из вида графика функции r = 2 sin 3

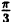

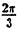

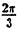
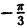

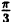

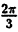

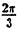
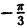

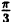
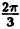

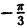
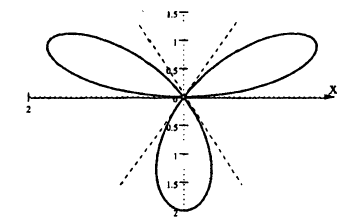

Такой график называют называют “трехлепестковая роза”.
Кривые второго порядка:
Определение 6.2. Кривой второго порядка называется линия, определяемая в декартовых координатах уравнением:
(6.3) Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = O.
Здесь коэффициенты — действительные числа и, по крайней мере, одно из чисел A₁B или C не равно нулю. Удобство таких обозначений для коэффициентов (2В, 2D, 2Е) станет ясно позже.
Всего существует три ’’реальных” кривых второго порядка: эллипс, (окружность — частный случай эллипса) гипербола и парабола, не считая такие линии, как ’’пара пересекающихся прямых” (ху = 0), «пара параллельных прямых” ((x — у)² — 4), ’’точка” ((x — 5)² + (у — 1)² = 0), ’’прямая” (х — 1)² = 0) и ’’мнимые кривые” (x² + y² + 5 = 0), которым не соответствует ни одна точка.
Окружность
Ранее было получено уравнение ( 6.2) окружности с центром в точке M(а; b), радиусом R. Это уравнение вида ( 6.3), т.е. окружность есть кривая второго порядка — можно показать, что уравнение (6.3), в котором A = C и B = O c помощью дополнения до полного квадрата каждой группы членов Ax² + 2Dx и By² + 2Еу приводится к виду (6.2), определяющему окружность радиуса R, или к виду: (х — а)² + (у — b)² = -R², не определяющему линию при R ≠ 0. Покажем это на примере.
Пример:
Показать, что уравнение 2x² + 2y² — 4x + 8y — 13 = 0 определяет окружность.
Решение: Поделив обе части на 2, получим уравнение в виде: x² + y² — 2x + 4y — 6,5 = 0 или, выделяя полный квадрат: (x² — 2х + 1) + (у² + 4y + 4) = 11,5 ⇔ (х — 1)² + (у + 2)² =11,5. Мы получим уравнение окружности с центром M(1; —2) и радиусом R = √11,5.
Пример:
Показать, что уравнение х² + у² + 6х — 6у + 22 = 0 не определяет никакой линии.
Решение:
Аналогично предыдущему, выделяя полный квадрат, получаем: х² + у² + 6х — 6у + 22 = 0 ⇔ (х² + 6х + 9) + (у² — 6у + 9) = — 4 ⇔ (x + 3)² + (y — 3)² =-4.
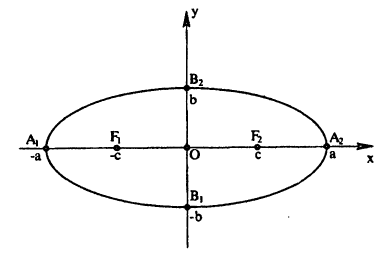
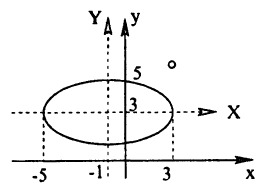
Эллипс
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равна постоянной величине.
Обозначим фокусы F₁ и F₁, расстояние между ними 2с, а сумму расстояний до них от точек эллипса через 2а (2а > 2с). Выберем декартову систему координат как показано на рис. 72. По определению эллипса: MF₁ + MF₂ = 2а. Пользуясь формулой (2.6) получаем:
Обозначив b² = a² — с² > 0, получаем: b²x² + a²y² — a²b² или:
(6.4)
Уравнение ( 6.4) называется каноническим уравнением эллипса, а и b — полуосями, а — большая полуось, b — малая, т.к. b = 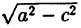
Так как 2а > 2с, то ε т.е. тем меньше эллипс вытянут вдоль фокальной оси Ох. В пределе, при ε → 0,a = b и получается окружность x² + у² = а² радиусом а При этом с = 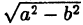
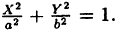
(6.5)
Гипербола
Определение 6.4. Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равен постоянной величине.
Обозначим фокусы F₁ и F₂, расстояние между ними 2с, а модуль разности расстояний до них от точек гиперболы через 2a (2c > 2a > 0). Выберем декартову систему координат, как показано на рис. 72. По определению гиперболы: MF₁ — MF₂ = ±2а. Пользуясь формулой (2.6), аналогично тому, как это было сделано для эллипса, получаем:
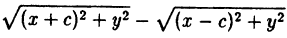
Уравнение (6.6) называется каноническим уравнением гиперболы, а и b — полуосями, а — действительной полуосью, b — мнимой. Так как х и у входят в уравнение только в четных степенях, гипербола симметрична относительно осей Ox и Оу. Выразив у из уравнения ( 6.6), получаем: 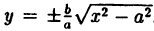
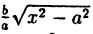
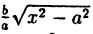
Точки пересечения гиперболы с осью Ox (фокальной осью) называются ее вершинами A₂(а;0), A₁(-a;0). C осью ординат гипербола не пересекается, поэтому фокальная ось называется действительной осью (а — действительная полуось), а перпендикулярная ей ось — мнимой осью (b — мнимая полуось). Можно показать, что при неограниченном возрастании абсциссы точка гиперболы неограниченно приближается к прямой у = 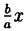
Отношение 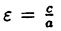
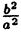
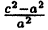
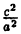
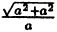
(6.7)
Уравнение асимптот такой гиперболы будет: у — y₀ =
Парабола
Определение:
Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой d, называемой директрисой (F ∉ d).
Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Выберем декартову систему координат как показано на рис. 75.
По определению параболы MF=MN. Из рис. 75. ясно, что:
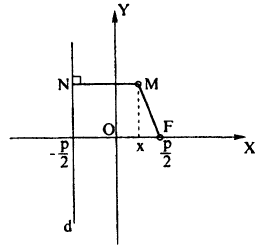
Приравнивая, получаем:
(6.8) у² = 2рх
Уравнение ( 6.8) называется каноническим уравнением параболы. Т.к. у входит в уравнение в четной степени, парабола симметрична относительно оси Ох. Выразив у из уравнения, получаем: у = 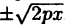
Ось симметрии параболы называется фокальной осью (ось Ox на рис. 76), точка пересечения пораболы с ней называется вершиной пораболы (точка О на рис. 76). Если вершина параболы находится в точке P(x₀; у₀), фокальная ось параллельна и одинаково направлена с осью Ox и расстояние от директрисы до фокуса равно Р, то с помощью параллельного переноса осей координат нетрудно получить уравнение такой параболы:
(6.9) (y — y₀)² = 2p(x -х₀)
Пример:
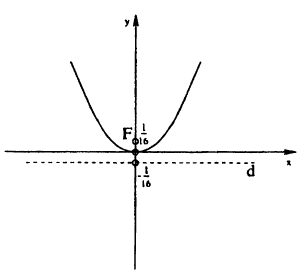
Найти фокус, директрису, фокальную ось для параболы у= 4x².
Решение:
Как известно, осью симметрии параболы у = х² является ось Оу, а вершиной — точка О, поэтому фокальной осью будет ось Оу, вершиной — начало координат.
Для определения фокуса и директрисы запишем уравнение данной параболы в виде: x² = 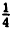
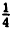
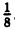
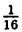
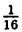
Понятие о приведении общего уравнения второго порядка к каноническому виду
Если в общем уравнении кривой второго порядка ( 6.3)
Ax² + 2Bxy + Cy² + 2Dx + 2Ey +F = 0
коэффициент 2B ≠ 0, то методами, которые будут изложены позже (лекция 34) это уравнение преобразуется к виду, в котором отсутствует член с произведением координат (т.е. 2В — 0).
Для приведения к каноническому виду уравнения ( 6.3), в котором 2В = 0, необходимо дополнить члены, содержащие х и у, до полных квадратов.
Если при этом (В = 0) А = С, то получится окружность (пример 6.3), точка или мнимая окружность (пример 6.4).
Если при этом (В = 0) A ≠ C и A ∙ C > 0, то получится эллипс (пример 6.8) или мнимый эллипс.
Если при этом (В = 0) A ≠ C и A ∙ C 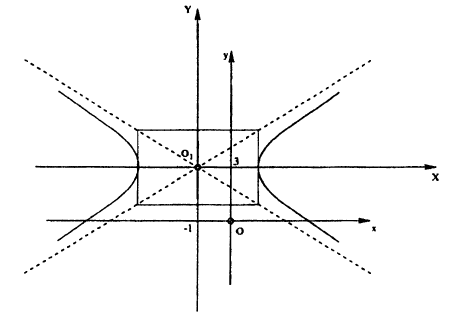
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² — 6x — 4y + 29 = 0.
Решение:
Выделим полный квадрат: x² — 6x — 4y + 29 = 0 ⇔ x² — 6x + 9 = 4y — 20 ⇔ (x — 3)² = 4(у — 5). Сделав замену координат X =х — 3, Y = у — 5 мы получим каноническое уравнение параболы X² = 4Y с осью OY и параметром р = 2. Таким образом исходная парабола имела вершину A(3; 5) и ось х = 3 параллельную оси Oy (рис. 79).
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² + 4y² + 2x — 24y + 21 =0.
Решение:
Выделив полный квадрат, получим уравнение: (x + 1)² + 4(у — 3)² = 16. Сделав замену координат: X = х + 1, Y = y — 3, получим каноническое уравнение эллипса: X² + AY² ⇔ 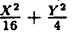
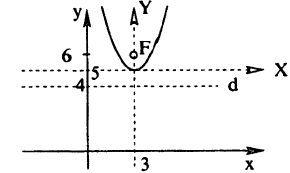
Видео:11 класс, 52 урок, ЭллипсСкачать

Решение заданий на тему: Кривые второго порядка
Пример:
Составьте уравнение окружности, имеющей центр 0(2; —5) и радиус R = 4.
Решение:
В соответствии с формулой (6.2) искомое уравнение имеет вид: (х — 2)² + (у + 5)² = 16.
Ответ: (х — 2)² + (у + 5)² = 16.
Пример:
Составьте уравнение эллипса, зная, что сумма полуосей равна 8 и расстояние между фокусами равно 8.
Решение:
Из условия имеем: a + b = 8, 2c = 8. C учетом того, что b² = а² — с², находим с = 4, а = 5, b = 3. Искомое уравнение эллипса будет: 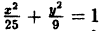
Ответ:
Пример:
Составьте уравнение гиперболы, зная, что фокусы F₁(10;0) и F₂(-10; 0) и что гипербола проходит через точку M(12; 3√5)
Решение:
Из условия имеем: с = 10, |MF₁ — MF₂|= 2а ⇔ 2а = 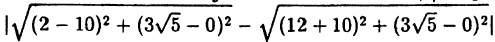
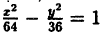
Ответ: 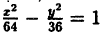
Пример:
Составьте уравнение параболы, зная, что фокус имеет координаты (5;0), а ось ординат является директрисой.
Решение:
Поскольку расстояние от директрисы параболы до ее полюса равно параметру р, а вершина находится на середине, из условия следует, что р = 5 и вершина расположена в точке A(2,5;0). Таким образом, в новых координатах X = х — 2,5; У = у каноническое уравнение параболы будет: Y² = 10Х, а в старых координатах: у² = 10(х — 2,5).
Ответ: y² = 10x — 25.
Пример:
Приведите к каноническому виду уравнение x² + y² — 2х + 6у — 5 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат: х² — 2х + у² + 6у — 5 = 0 ⇔ x² — 2x + 1 + у² + 6у + 9 — 1 — 9 — 5 = 0 ⇔ (х — 1)² + (у + 3)² = 15
В соответствии с формулой (6.2) это есть уравнение окружности с центром в точке A(1; -3), радиусом √5.
Ответ: (х — 1)² + (у + 3)² = 15.
Пример:
Приведите к каноническому виду уравнение x² + 4у² + 4х — 16у — 8 = 0, определите вид кривой и ее параметры:
Решение:
Выделим полный квадрат: x² + 4х + 4у² — 16y -8 = 0 ⇔ x²+4x + 4 + 4y²- 16y + 16-4-16-8 = 0 ⇔ (x + 2)² + 4(y²-4у+ 4) -28 ⇔ (х + 2)² + 4(y — 2)² = 28 ⇔ 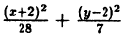
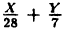
Ответ: 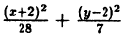
Пример:
Приведите к каноническому виду уравнение x² + 2y² + 8x — 4 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат:
x²+2y²+8x-4 = 0 ⇔ x²+8x+16+2y²-16-4 =0 ⇔ (x+4)²+2y2-20 = 0 ⇔ 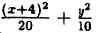
Сделав замену координат X = х + 4, Y — у, убеждаемся, что эта кривая — эллипс, с полуосями a = 2√5 и b = √10 и центром A(-4;0).
Ответ: 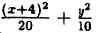
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎦 Видео
Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Урок 16: Эксцентриситет и директрисы (теория)Скачать

Определить тип кривой (эллипс)Скачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать