Эллипс каноническое уравнение смещенный центр

Отрезок B₁B₂ = 2b называется (при а > b) малой осью эллипса; 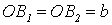– малая полуось эллипса.

3. ; ; и существует, если или , (от А₁ до А₂).

; и существует, если (от В₁ до В₂).

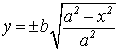
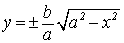
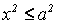
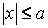
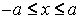
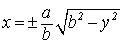
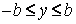
4. Степень вытянутости эллипса определяет параметр – эксцентриситет:

или , .

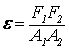
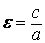
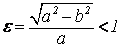
Если a = b, то имеем окружность с центром в т.О(0;0) и радиуса а. В этом случае .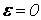

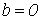
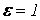
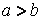
Если , то имеем отрезок А₁А₂ и . Эллипс (при ) получен равномерным сжатием окружности сверху – снизу.

Аналогично можно рассмотреть случай, когда фокусы F₁F₂ расположены на оси ОУ ().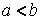

Пример: построение эллипса по каноническому уравнению и отыскание его параметров...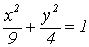

б) Смещенный эллипс

– уравнение смещенного эллипса. Центр расположен в т. С(α;β).

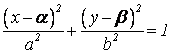
При построении смещенного эллипса применяется преобразование системы координат – параллельный перенос.

ХОУ – старая система координат;

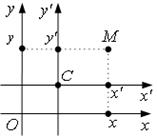
т.О(0;0) – начало координат;

Х’СУ’ – новая система координат; т.С(α,β) – ее начало координат.

, , масштабная единица одна и та же.

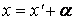
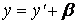
Возьмем на плоскости произвольно т.М. В системе ХОУ ее координаты х,у; в системе Х’СУ’ – х’,у’ , причем ; . Отсюда

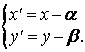
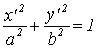
Сделаем в уравнении смещенного эллипса замену переменной по формулам , получим каноническое уравнение эллипса .

Строим эллипс по его каноническому уравнению в системе Х’СУ’.

Пример: построение эллипса, заданного в смещенном виде: .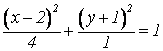

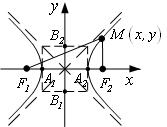
3.3 Гипербола – ГМТ плоскости, модуль разности расстояний которых до двух фиксированных точек плоскости – фокусов F₁, F₂ – постоянен и равен числу 2а.

а) Каноническое уравнение

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 266
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 602
• БГУ 153
• БГУИР 391
• БелГУТ 4908
• БГЭУ 962
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 119
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1967
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 300
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 409
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 497
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 130
• ИжГТУ 143
• КемГППК 171
• КемГУ 507
• КГМТУ 269
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2909
• КрасГАУ 370
• КрасГМУ 630
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 139
• КубГУ 107
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 367
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 330
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 636
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 454
• НИУ МЭИ 641
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 212
• НУК им. Макарова 542
• НВ 777
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1992
• НГУЭУ 499
• НИИ 201
• ОмГТУ 301
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 119
• РАНХиГС 186
• РОАТ МИИТ 608
• РТА 243
• РГГМУ 118
• РГПУ им. Герцена 124
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 122
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 130
• СПбГАСУ 318
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 147
• СПбГПУ 1598
• СПбГТИ (ТУ) 292
• СПбГТУРП 235
• СПбГУ 582
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 193
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 380
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1655
• СибГТУ 946
• СГУПС 1513
• СибГУТИ 2083
• СибУПК 377
• СФУ 2423
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 324
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 306

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Кривые второго порядка. Алгебраической кривой второго порядка называется кривая Г, уравнение которой в декартовой системе координат имеет вид:

Аx 2 + 2Вxy + Сy 2 + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю.

Если кривая Г невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):

Эллипс – геометрическое множество точек плоскости, сумма расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами 2c:

Эллипс, заданный каноническим уравнением: симметричен относительно осей координат. Параметры а и b называются полуосями эллипса (большой и малой соответственно), точки , , , называются его вершинами. Если а>b, то фокусы находятся на оси ОХ на расстоянии от центра эллипса О.

называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при эллипс является окружностью, а при он вырождается в отрезок длиною ). Если а

Гипербола, заданная каноническим уравнением:

симметрична относительно осей координат. Она пересекает ось ОХ в точках и – вершинах гиперболы, и не пересекает оси ОY. Параметр а называется вещественной полуосью, b – мнимой полуосью. Число

называется эксцентриситетом гиперболы. Прямые

называются асимптотами гиперболы.

Гипербола, заданная каноническим уравнением:

называется сопряжённой (имеет те же асимптоты). Её фокусы расположены на оси OY.

Она пересекает ось ОY в точках и – вершинах гиперболы, и не пересекает оси ОX.В этом случае параметр b называется вещественной полуосью, a – мнимой полуосью. Эксцентриситет вычисляется по формуле:

Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой: .

Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.

задает параболу, симметричную относительно оси ОY. Парабола

имеет фокус и директрису

имеет фокус и директрису

Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р 2 + 2Вxy + Сy 2 + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю.

Оно задаёт кривую второго порядка. Наша цель: поменять систему координат так, чтобы максимально упростить данное уравнение. Для этого сначала (если B0) повернём искодный базис (координатные оси Ox и Oy) на угол б против часовой стрелки таким образом, чтобы новые оси Ox’ и Oy’ стали параллельны осям кривой, при этом исчезнет слагаемое 2Вxy:

– матрица линейного преобразования: поворот на угол б против часовой стрелки.

A(x’cosб – y’sinб) 2 + 2B(x’cosб – y’sinб)(x’sinб + y’cosб)+C(x’sinб + y’cosб) 2 + 2D(x’cosб – y’sinб) + 2E(x’sinб + y’cosб) + F = 0

Выберем угол б так, чтобы коэффициент при произведении x’y’ обратился в ноль, т.е. чтобы выполнялось равенство:

-2Acosбsinб + 2B(cos 2 б – sin 2 б) + 2Csinбcosб = 0

В новой системе координат Ox’y’ (после поворота на угол б), учитывая, что

уравнение будет иметь вид

А’x’ 2 + С’y’ 2 + 2D’x’ + 2Е’y’ + F’ = 0,

где коэффициенты А’ и С’ не равны одновременно нулю.

Следующий этап упрощения заключается в параллельном переносе осей Ox’ и Oy’ до совпадения их с осями кривой, при этом начало координат совпадёт с центром (или вершиной, в случае параболы) кривой. Техника преобразований на данном этапе заключается в выделении полного квадрата.

Таким образом, мы получим канонические уравнения кривых второго порядка. Всего возможны 9 качественно различных случаев (включая случаи вырождения и распадения):

• 4. (мнимый эллипс),
• 5. (пара мнимых параллельных прямых),
• 6. (пара параллельных прямых),
• 7. (пара совпавших прямых),
• 8. (точка (пара мнимых пересекающихся прямых)),
• 9. (пара пересекающихся прямых).

Кривые 2-го порядка со смещенными центрами (вершинами).

Если в общем уравнении кривой 2-го порядка

в частности, В = 0, то есть отсутствует член с произведением переменных, то это означает, что оси кривой параллельны координатным. Рассмотрим уравнение:

• (A и C одновременно). Можно показать, что при этом:1) Если АС > 0 (коэффициенты при квадратах переменных одного знака), то уравнение определяет эллипс;
• 2) Если АС

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет.

Кафедра «Товароведение и экспертиза потребительских товаров»

«Кривые второго порядка: эллипс, окружность, парабола, гипербола»

По дисциплине Высшая математика.

Пермина Александра Николаевна

студент группы 131

Кравченко Ольга Владимировна

Кривые второго порядка: эллипс, окружность, парабола, гипербола.

Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Кривая второго порядка на плоскости в прямоугольной системе координат описывается уравнением:

Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F ₁ и F ₂ есть заданная постоянная величина, называется эллипсом.

Каноническое уравнение эллипса.

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Число a называют большой полуосью эллипса, а число b – его малой полуосью.

• Фокальное свойство. Если F₁ и F₂ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой ( F₁X) равен углу между этой касательной и прямой ( F₂X) .
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида.
• Эксцентриситетом эллипса называется отношение

Эллипс также можно описать как

• фигуру, которую можно получить из окружности, применяя аффинное преобразование
• ортогональную проекцию окружность на плоскость.
• Пересечение плоскости и кругового цилиндра.

Каноническое уравнение окружности.

Общее уравнение окружности записывается как:

Уравнение окружности радиуса R с центром в начале координат:

• Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
• Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Точка касания двух окружностей лежит на линии, соединяющей их центры.
• Длину окружности с радиусом R можно вычислить по формуле C = 2π R.
• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.

• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.

Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

где р (фокальный параметр) – расстояние от фокуса до директрисы

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
• Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе. Для параболы с вершиной в начале координат (0; 0) и положительным направлением ветвей фокус находится в точке (0; 0,25).
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Парабола является антиподерой прямой.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

· Прямая пересекает параболу не более чем в двух точках.

· Эксцентриситет параболы е=1.

Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.

· Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

· Каждая гипербола имеет пару асимптот:

· Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы

· Эксцентриситетом гиперболы называется величина е = с / а.Эксцентриситет гиперболы e> 1

· Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы

Видео:Написать каноническое уравнение эллипса, если известны b и cСкачать

Эллипс

Видео:§18 Каноническое уравнение эллипсаСкачать

Определение эллипса.

Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>+frac<y^><b^>=1label
$$
при условии (a geq b > 0).

Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).

Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.

Рис. 8.1. Эллипс

В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_), (M_) и (M_) (рис. 8.1). Следовательно, справедливо следующее утверждение.

Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.

Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^+y^=a^). При каждом (x) таком, что (|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Фокусами называются точки (F_) и (F_) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Отметим, что (varepsilon Утверждение 2.

Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_=|F_M|=a-varepsilon x, r_=|F_M|=a+varepsilon x.label
$$

Очевидно, что (r_^=(x-c)^+y^). Подставим сюда выражение для (y^), найденное из уравнения эллипса. Мы получим
$$
r_^=x^-2cx+c^+b^-frac<b^x^><a^>.nonumber
$$

Учитывая равенство eqref, это можно преобразовать к виду
$$
r_^=a^-2cx+frac<c^x^><a^>=(a-varepsilon x)^.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).

Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_+r_=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^+y^>=2a-sqrt<(x+c)^+y^>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=asqrt<(x+c)^+y^>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^x^+a^y^=a^b^), равносильному уравнению эллипса eqref.

Рис. 8.4. Фокусы и директрисы эллипса.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).

Видео:Видеоурок "Гипербола"Скачать

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_(x_, y_)) — точка на эллипсе и (y_ neq 0). Через (M_) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ > 0) это график (f_(x)=bsqrt<1-x^/a^>), для (y_ Утверждение 5.

Касательная к эллипсу в точке (M_(x_, y_)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Рис. 8.5.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Каноническое уравнение окружности со смещенным центром имеет вид

Видео:Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

окружность

Определение: Окружность — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.

Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R — радиус окружности; х,у — текущие координаты точек, лежащих на окружности.

Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.

Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь

Построение окружности выполняется с помощью циркуля.

Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

эллипс

Определение: Эллипс — это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.

Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:

где а и в — полуоси, х,у — текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.

При рассмотрении эллипса возможны два случая:

• 1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в — малая полуось, лежащая на координатной оси Оу;
• 2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.

Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:

где величина «с» определяет фокусное расстояние.

Для характеристики формы эллипса вводится эксцентриситет.

Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:

=, если ав и =, если ва.

Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).

Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.

В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) — основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.

Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:

Построение эллипса рассмотрим ниже на примерах.

Пример. Определить вид, параметры и построить линию, заданную уравнением:

Решение: 1. Это эллипс с несмещенным центром вида:

2. Найдем параметры: — большая полуось на оси Ох;

— малая полуось на оси Оу;

Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.

• 3. Построение эллипса (см. рисунок выше) выполним по этапам:
• 1) строим систему координат Оху;
• 2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
• 3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
• 4) вписываем эллипс в осевой прямоугольник;
• 5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Видео:166. Найти каноническое уравнение эллипса.Скачать

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Видео:11 класс, 52 урок, ЭллипсСкачать

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Эллипс со смещенным центром

Отрезок B₁B₂ = 2b называется (при а > b) малой осью эллипса; 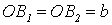– малая полуось эллипса.

3. ; ; и существует, если или , (от А₁ до А₂).

; и существует, если (от В₁ до В₂).

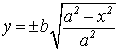
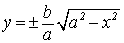
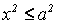
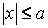
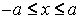
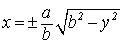
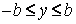
4. Степень вытянутости эллипса определяет параметр – эксцентриситет:

или , .

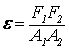
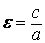
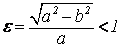
Если a = b, то имеем окружность с центром в т.О(0;0) и радиуса а. В этом случае .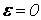

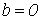
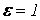
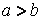
Если , то имеем отрезок А₁А₂ и . Эллипс (при ) получен равномерным сжатием окружности сверху – снизу.

Аналогично можно рассмотреть случай, когда фокусы F₁F₂ расположены на оси ОУ ().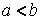

Пример: построение эллипса по каноническому уравнению и отыскание его параметров...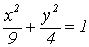

б) Смещенный эллипс

– уравнение смещенного эллипса. Центр расположен в т. С(α;β).

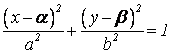
При построении смещенного эллипса применяется преобразование системы координат – параллельный перенос.

ХОУ – старая система координат;

т.О(0;0) – начало координат;

Х’СУ’ – новая система координат; т.С(α,β) – ее начало координат.

, , масштабная единица одна и та же.

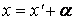
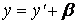
Возьмем на плоскости произвольно т.М. В системе ХОУ ее координаты х,у; в системе Х’СУ’ – х’,у’ , причем ; . Отсюда

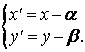
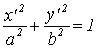
Сделаем в уравнении смещенного эллипса замену переменной по формулам , получим каноническое уравнение эллипса .

Строим эллипс по его каноническому уравнению в системе Х’СУ’.

Пример: построение эллипса, заданного в смещенном виде: .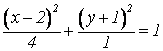

3.3 Гипербола – ГМТ плоскости, модуль разности расстояний которых до двух фиксированных точек плоскости – фокусов F₁, F₂ – постоянен и равен числу 2а.

а) Каноническое уравнение

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 266
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 602
• БГУ 153
• БГУИР 391
• БелГУТ 4908
• БГЭУ 962
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 119
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1967
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 300
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 409
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 497
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 130
• ИжГТУ 143
• КемГППК 171
• КемГУ 507
• КГМТУ 269
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2909
• КрасГАУ 370
• КрасГМУ 630
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 139
• КубГУ 107
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 367
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 330
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 636
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 454
• НИУ МЭИ 641
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 212
• НУК им. Макарова 542
• НВ 777
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1992
• НГУЭУ 499
• НИИ 201
• ОмГТУ 301
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 119
• РАНХиГС 186
• РОАТ МИИТ 608
• РТА 243
• РГГМУ 118
• РГПУ им. Герцена 124
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 122
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 130
• СПбГАСУ 318
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 147
• СПбГПУ 1598
• СПбГТИ (ТУ) 292
• СПбГТУРП 235
• СПбГУ 582
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 193
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 380
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1655
• СибГТУ 946
• СГУПС 1513
• СибГУТИ 2083
• СибУПК 377
• СФУ 2423
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 324
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 306

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Кривые второго порядка. Алгебраической кривой второго порядка называется кривая Г, уравнение которой в декартовой системе координат имеет вид:

Аx 2 + 2Вxy + Сy 2 + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю.

Если кривая Г невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):

Эллипс – геометрическое множество точек плоскости, сумма расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами 2c:

Эллипс, заданный каноническим уравнением: симметричен относительно осей координат. Параметры а и b называются полуосями эллипса (большой и малой соответственно), точки , , , называются его вершинами. Если а>b, то фокусы находятся на оси ОХ на расстоянии от центра эллипса О.

называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при эллипс является окружностью, а при он вырождается в отрезок длиною ). Если а

Гипербола, заданная каноническим уравнением:

симметрична относительно осей координат. Она пересекает ось ОХ в точках и – вершинах гиперболы, и не пересекает оси ОY. Параметр а называется вещественной полуосью, b – мнимой полуосью. Число

называется эксцентриситетом гиперболы. Прямые

называются асимптотами гиперболы.

Гипербола, заданная каноническим уравнением:

называется сопряжённой (имеет те же асимптоты). Её фокусы расположены на оси OY.

Она пересекает ось ОY в точках и – вершинах гиперболы, и не пересекает оси ОX.В этом случае параметр b называется вещественной полуосью, a – мнимой полуосью. Эксцентриситет вычисляется по формуле:

Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой: .

Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.

задает параболу, симметричную относительно оси ОY. Парабола

имеет фокус и директрису

имеет фокус и директрису

Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р 2 + 2Вxy + Сy 2 + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю.

Оно задаёт кривую второго порядка. Наша цель: поменять систему координат так, чтобы максимально упростить данное уравнение. Для этого сначала (если B0) повернём искодный базис (координатные оси Ox и Oy) на угол б против часовой стрелки таким образом, чтобы новые оси Ox’ и Oy’ стали параллельны осям кривой, при этом исчезнет слагаемое 2Вxy:

– матрица линейного преобразования: поворот на угол б против часовой стрелки.

A(x’cosб – y’sinб) 2 + 2B(x’cosб – y’sinб)(x’sinб + y’cosб)+C(x’sinб + y’cosб) 2 + 2D(x’cosб – y’sinб) + 2E(x’sinб + y’cosб) + F = 0

Выберем угол б так, чтобы коэффициент при произведении x’y’ обратился в ноль, т.е. чтобы выполнялось равенство:

-2Acosбsinб + 2B(cos 2 б – sin 2 б) + 2Csinбcosб = 0

В новой системе координат Ox’y’ (после поворота на угол б), учитывая, что

уравнение будет иметь вид

А’x’ 2 + С’y’ 2 + 2D’x’ + 2Е’y’ + F’ = 0,

где коэффициенты А’ и С’ не равны одновременно нулю.

Следующий этап упрощения заключается в параллельном переносе осей Ox’ и Oy’ до совпадения их с осями кривой, при этом начало координат совпадёт с центром (или вершиной, в случае параболы) кривой. Техника преобразований на данном этапе заключается в выделении полного квадрата.

Таким образом, мы получим канонические уравнения кривых второго порядка. Всего возможны 9 качественно различных случаев (включая случаи вырождения и распадения):

• 4. (мнимый эллипс),
• 5. (пара мнимых параллельных прямых),
• 6. (пара параллельных прямых),
• 7. (пара совпавших прямых),
• 8. (точка (пара мнимых пересекающихся прямых)),
• 9. (пара пересекающихся прямых).

Кривые 2-го порядка со смещенными центрами (вершинами).

Если в общем уравнении кривой 2-го порядка

в частности, В = 0, то есть отсутствует член с произведением переменных, то это означает, что оси кривой параллельны координатным. Рассмотрим уравнение:

• (A и C одновременно). Можно показать, что при этом:1) Если АС > 0 (коэффициенты при квадратах переменных одного знака), то уравнение определяет эллипс;
• 2) Если АС

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет.

Кафедра «Товароведение и экспертиза потребительских товаров»

«Кривые второго порядка: эллипс, окружность, парабола, гипербола»

По дисциплине Высшая математика.

Пермина Александра Николаевна

студент группы 131

Кравченко Ольга Владимировна

Кривые второго порядка: эллипс, окружность, парабола, гипербола.

Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Кривая второго порядка на плоскости в прямоугольной системе координат описывается уравнением:

Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F ₁ и F ₂ есть заданная постоянная величина, называется эллипсом.

Каноническое уравнение эллипса.

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Число a называют большой полуосью эллипса, а число b – его малой полуосью.

• Фокальное свойство. Если F₁ и F₂ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой ( F₁X) равен углу между этой касательной и прямой ( F₂X) .
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида.
• Эксцентриситетом эллипса называется отношение

Эллипс также можно описать как

• фигуру, которую можно получить из окружности, применяя аффинное преобразование
• ортогональную проекцию окружность на плоскость.
• Пересечение плоскости и кругового цилиндра.

Каноническое уравнение окружности.

Общее уравнение окружности записывается как:

Уравнение окружности радиуса R с центром в начале координат:

• Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
• Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Точка касания двух окружностей лежит на линии, соединяющей их центры.
• Длину окружности с радиусом R можно вычислить по формуле C = 2π R.
• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.

• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.

Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

где р (фокальный параметр) – расстояние от фокуса до директрисы

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
• Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе. Для параболы с вершиной в начале координат (0; 0) и положительным направлением ветвей фокус находится в точке (0; 0,25).
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Парабола является антиподерой прямой.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

· Прямая пересекает параболу не более чем в двух точках.

· Эксцентриситет параболы е=1.

Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.

· Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

· Каждая гипербола имеет пару асимптот:

· Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы

· Эксцентриситетом гиперболы называется величина е = с / а.Эксцентриситет гиперболы e> 1

· Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы

📺 Видео

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

ЭллипсСкачать

Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать

165. Найти фокусы и эксцентриситет эллипса.Скачать