Эллипс его геометрические свойства уравнения

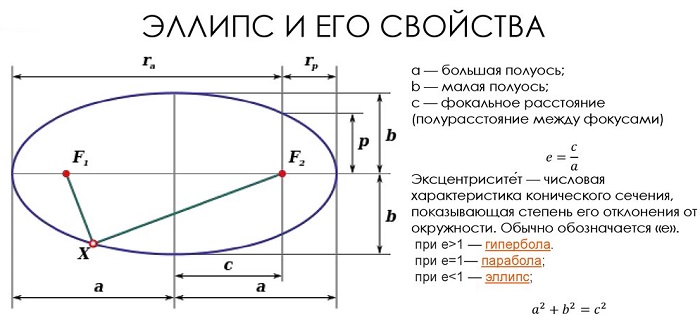
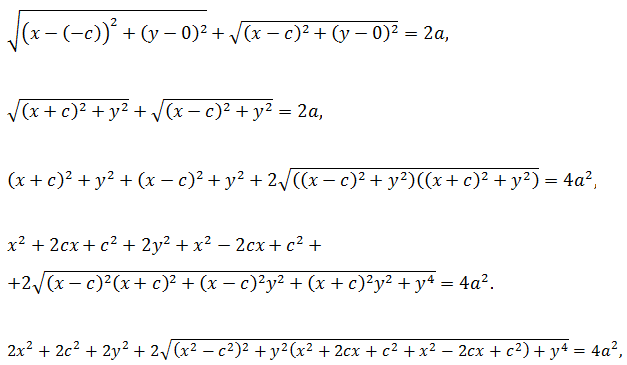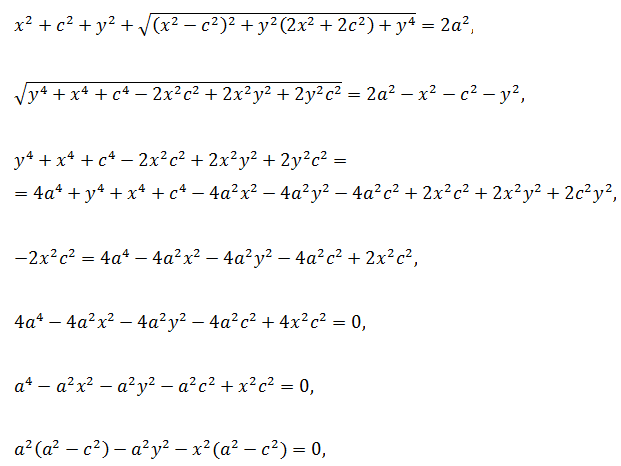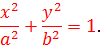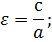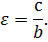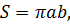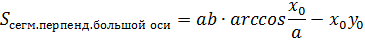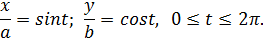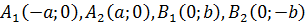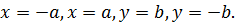Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная. При совпадении точек F₁ и F₂ эллипс превращается в окружность. Выведем уравнение эллипса, выбрав декартову систему

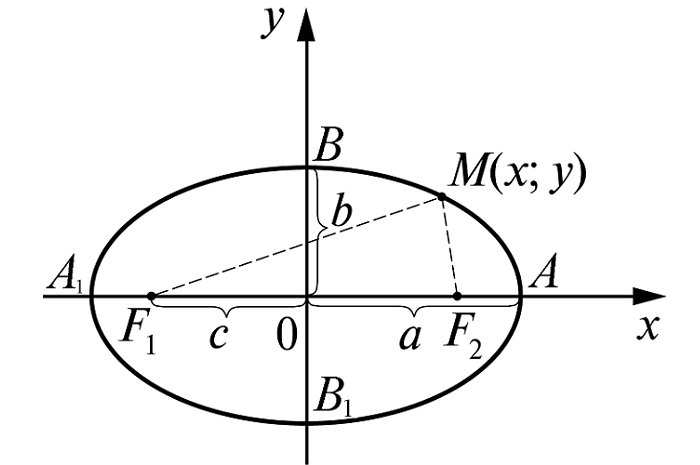
координат так, чтобы ось Ох совпала с прямой F₁F₂, начало координат – с серединой отрезка F₁F₂. Пусть длина этого отрезка равна 2с, тогда в выбранной системе координат F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F₁ и F₂ равна 2а. Тогда r₁ + r₂ = 2a, но 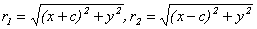, поэтому Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:

Эксцентриситетом эллипса называется величина е=с/а. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Свойства эллипса:

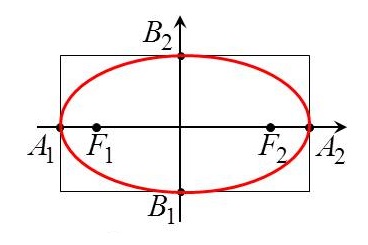
1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b(2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника

3)Эксцентриситет эллипса e a, а весь эллипс лежит в прямоугольнике )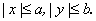

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Эллипс — свойства, уравнение и построение фигуры

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Видео:ЭллипсСкачать

Определение и элементы эллипса

Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

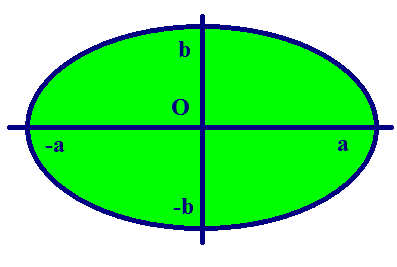
По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Уравнение эллипса

Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F₁(-c;0); F₂(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

a 2 b 2 = a 2 y 2 + x 2 b 2 ,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Видео:7.2. Эллипс. Свойства эллипсаСкачать

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

Видео:Видеоурок "Гипербола"Скачать

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Видео:11 класс, 52 урок, ЭллипсСкачать

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Видео:Видеоурок "Эллипс"Скачать

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Видео:Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

Видео:Оптическое свойство эллипса и его применение в медицинеСкачать

Основные свойства эллипса

В данной публикации мы рассмотрим основные свойства эллипса, сопроводив их наглядными рисунками для лучшего восприятия представленной информации.

Примечание: определение эллипса, его основные элементы и уравнение мы рассмотрели в отдельной публикации.

Видео:#198. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛАСкачать

Геометрические свойства эллипса

Свойство 1

Угол между касательной, проведенной к эллипсу, и фокальным радиусом r₁ равняется углу между этой же касательной и фокальным радиусом r₂.

• r₁ и r₂ – фокальные радиусы эллипса;
• Точка M – место соприкосновения касательной и эллипса;
• α – равные углы между касательной и фокальными радиусами.

Свойство 2

Уравнение касательной, проведенной к эллипсу (касание в точке M) с координатами ( x_M, y_M) выглядит следующим образом:

Свойство 3

Допустим эллипс пересекают две параллельные прямые. Отрезок, который соединяет середины отрезков, получившихся при пересечении прямых и эллипса, всегда будет проходит через центр фигуры.

• M₁M₂ и N₁N₂ – отрезки, образованные в результате пересечения эллипса двумя параллельными прямыми.
• MN – отрезок, соединяющий середины M₁M₂ и N₁N₂;
• MN проходит через центр эллипса (точка O).

Свойство 4

Допустим эллипс с фокусами F₁ и F₂ вписан в треугольник ABC.

В этом случае справедливо соотношение ниже:

🔥 Видео

Эллипс | Элементы аналитической геометрииСкачать

§18 Каноническое уравнение эллипсаСкачать

§28 Эксцентриситет эллипсаСкачать

§17 Определение эллипсаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Эллипс. Построение и параметры | Аналитическая геометрияСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать