Алгебра и теория чисел
Лекция 3
Системы линейных уравнений
План
1. Основные понятия и обозначения.
2. Элементарные преобразования системы линейных уравнений.
3. Ступенчатая матрица. Приведение матрицы к ступенчатому виду.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.
2. Ермаков В.И. Общий курс высшей математики. М.: Инфра — М, 2000. с. 5-22
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.
1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений — метод последовательного исключения неизвестных или метод Гаусса по имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).
Определение 1.Системой m линейных уравнений с n неизвестными

где a11 ,a12 . amn — фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые коэффициентами при неизвестных, b1 ,b2 . bm — фиксированные числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 2.Решением системы линейных уравнений (1) называется такой упорядоченный набор n чисел 
Система называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет одно решение, и называется неопределенной, если она не имеет решений.
Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 — множества их решений соответственно.
Определение 3.Говорят, что система линейных уравнений S2 следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т.е. 

Определение 4. Говорят, что системы S1 и S2 равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т.е. 

Отношение следования и равносильности обладают следующими свойствами.
1. Если 


Действительно, если 

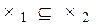



2. 
3. Если 

4. Если 
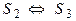
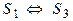
Свойства 2, 3, 4 доказываются аналогично.
Элементарные преобразования системы линейных уравнений.
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство.В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной .
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число k,получим верное числовое равенство:

т.о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы . Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число k , получим систему

Пусть 




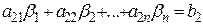
Прибавляя почленно к первому равенству второе, умноженное на число k получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Ступенчатая матрица.
Определение 6.Матрицей размерности 
содержащая mn чисел, расположенных в m строк и n столбцов, числа 

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).







Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число 
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство.Доказательство проводим методом математической индукции по числу m строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих m-1 строку и докажем его для матриц, в которых содержится m строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер k , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
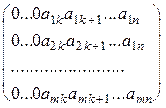
Можем считать, что элемент 




Рассмотрим матрицу, состоящую из последних m-1 строк матрицы (9):

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: 
где элементы 



элементы 


4. Метод Гаусса. Системе линейных уравнений (1) соответствуют три матриц



Первая матрица называется матрицей системы, вторая — расширенной или присойдиненной матрицей системы, третья — столбцом свободных членов.
Система линейных уравнений называется системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются главными неизвестными, а остальные неизвестные называются свободными.
Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т.е. уравнение вида:

не имеет решений. Действительно, если 

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.
Таким образом мы доказали первую часть следующей теоремы.
Теорема 3.Любую систему линейных уравнений , содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.
1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.
2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.
3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.
Доказательство.Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.
В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел 
В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:
В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

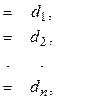
где 


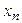




В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а
систему можно записать в виде:




где 




Следствие.Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.
Действительно, система однородных уравнений всегда имеет нулевое решение 
Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.
Пример 1.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:
В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:
Решение системы 
Пример 2.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

02. Элементарные преобразования системы линейных уравнений
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство. В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной.
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число K, получим верное числовое равенство:

Т. о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы. Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число K , получим систему

Пусть 





Прибавляя почленно к первому равенству второе, умноженное на число K получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Видео:Метод Гаусса для решения систем линейных уравнений. Элементарные преобразования матриц.Скачать

Равносильные системы уравнений, равносильные преобразования
В этой статье мы поговорим про равносильные системы уравнений. Здесь мы дадим соответствующее определение, а также разберем, какие существуют преобразования, позволяющие переходить от исходной системы уравнений к равносильной ей системе.
Навигация по странице.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Определение равносильных систем уравнений
В учебниках [1, с. 199; 2, с. 74] дается определение равносильных систем уравнений с двумя переменными:
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
В старших классах оно обобщается на системы с любым числом уравнений и переменных [3, с. 265] :
Две системы уравнений называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
Примеры равносильных и неравносильных систем приведем в следующем пункте.
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Равносильны ли данные системы уравнений?
Чтобы сделать вывод о равносильности или неравносильности данных систем уравнений на основе определения, надо наперед знать решения этих систем. Приведем пример. Пусть нам известно, что системы уравнений 

Чтобы доказать неравносильность систем уравнений, достаточно привести одно частное решение, являющееся решением одной системы, но не являющееся решением другой. Например, легко обосновать, что системы уравнений 

А как доказать равносильность систем уравнений, если их решения неизвестны? Конечно, можно найти решения, после чего сделать вывод касательно равносильности на основе определения. Но иногда для этого решать системы необязательно, это касается тех случаев, когда видно, что одна система получена из другой при помощи некоторых так называемых равносильных преобразований. Их мы подробно изучим в следующем пункте, а пока приведем пример.
Рассмотрим две системы уравнений 

Видео:Решение системы уравнений методом ГауссаСкачать

Равносильные преобразования систем уравнений
Существует ряд преобразований, позволяющих преобразовать данную систему уравнений в равносильную ей систему. Они получили название равносильных преобразований, и нашли основное применение при решении систем уравнений. Эти преобразования можно считать свойствами систем уравнений. Рассмотрим и обоснуем основные из них.
Перестановка местами уравнений системы дает равносильную систему уравнений.
Доказательство этого утверждения очевидно. В силу определения решения системы уравнений любое отдельно взятое решение системы уравнений является решением каждого уравнения этой системы. Понятно, что оно является и решением каждого уравнения системы с этими же уравнениями, но переставленными местами, значит, является решением и системы с переставленными местами уравнениями.
К примеру, 

Если любое уравнение в системе заменить равносильным уравнением, то полученная система будет равносильна исходной.
Доказательство этого факта тоже лежит на поверхности. Любое решение системы уравнений является решением каждого уравнения системы. Мы также знаем, что равносильные уравнения имеют одинаковые решения. Поэтому, любое решение исходной системы уравнений будет решением всех уравнений системы, в которой какое-то уравнение заменено равносильным ему уравнением, а значит, и решением этой системы.
Важность доказанного свойства огромна: оно дает нам право на работу с отдельными уравнениями системы. С ними мы можем проводить всевозможные уже знакомые нам равносильные преобразования, например, перестановку местами слагаемых, перенос слагаемых из одной части в другую с противоположным знаком, умножение или деление обеих частей уравнения на отличное от нуля число и т.д.
Приведем пример. Пусть дана система 

Если к левой и правой части одного из уравнений системы прибавить соответственно левую и правую часть другого уравнения системы, то полученная система будет равносильна исходной.
Для доказательства покажем, что любое решение изначальной системы уравнений является решением полученной, и обратно, что любое решение полученной системы является решением исходной. Это будет означать равносильность систем.
Любое решение начальной системы является решением каждого ее уравнения, оно обращает все уравнения в верные числовые равенства. Нам известно свойство числовых равенств, которое утверждает, что при почленном сложении верных числовых равенств получается верное равенство. Отсюда следует, что взятое нами решение начальной системы является решением уравнения, полученного в результате почленного прибавления к нему другого уравнения. Поэтому, это решение является решением и полученной системы уравнений, так как является решением каждого ее уравнения.
Теперь обратно. Возьмем любое решение полученной системы, оно является решением каждого ее уравнения, то есть, оно обращает их в верные числовые равенства. Существует свойство, позволяющее выполнять почленное вычитание верных числовых равенств. Вычтем из равенства, соответствующего уравнению, полученному в результате почленного сложения, равенство, соотетствующее прибавленному ранее уравнению. Это даст верное числовое равенство, отвечающее начальному уравнению системы до прибавления к нему другого уравнения. Отсюда следует, что взятое решение будет решением каждого уравнения исходной системы, а значит, и ее решением.
Приведем пример выполнения этого равносильного преобразования. Возьмем систему двух уравнений с двумя переменными 

Понятно, что если система содержит три или большее число уравнений, то можно не ограничиваться почленным прибавлением к левой и правой части выбранного уравнения левой и правой части одного уравнения, а прибавлять левые и правые части двух, трех, да хоть всех остальных уравнений системы. В результате этих действий все равно получится равносильная система уравнений.
На доказанном равносильном преобразовании базируется один из методов решения систем уравнений – метод алгебраического сложения.
Если одно из уравнений системы представляет собой переменную, выраженную через другие переменные, то в любое другое уравнение системы можно подставить вместо этой переменной ее выражение, система, полученная в результате такого преобразования, равносильна исходной.
Приведем пример для пояснения. Возьмем систему 

Пусть пара (x0, y0) – решение исходной системы, тогда x0=2·y0−1 и x0+3·y0−1=0 – верные числовые равенства. Докажем, что при этом равенство (2·y0−1)+3·y0−1=0 тоже верное, что будет доказывать, что (x0, y0) является решением системы, полученной после преобразования, а это будет означать, что полученная система имеет те же решения, что и исходная.
Легко показать, что при условии x0=2·y0−1 значения выражений x0+3·y0−1 и (2·y0−1)+3·y0−1 равны. Для этого составим их разность и покажем, что она равна нулю: x0+3·y0−1−((2·y0−1)+3·y0−1)= (x0−(2·y0−1))+(3·y0−1−(3·y0−1))= x0−(2·y0−1) , а полученное выражение равно нулю в силу равенства x0=2·y0−1 . Итак, справедливо равенство x0+3·y0−1=(2·y0−1)+3·y0−1 , но справедливо и равенство x0+3·y0−1=0 , а из них по свойству транзитивности вытекает справедливость равенства (2·y0−1)+3·y0−1=0 .
Аналогично доказывается, что любое решение системы уравнений 
Суть доказательства рассматриваемого утверждения в общем виде та же. То есть, показывается, что любое решение исходной системы является решением системы, полученной после преобразования, и обратно.
Это равносильное преобразование дает разрешение на решение систем уравнений методом подстановки.
В заключение скажем, что обычно при решении систем уравнений разобранные равносильные преобразования используются сообща и иногда по нескольку раз. Дальше на практике Вы увидите это.
🔥 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Теорема Кронекера-КапеллиСкачать

Системы линейных уравнений: Теорема Кронекера-КапеллиСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Билет 2 (Элементарные преобразования, эквивалентность, метод Гаусса)Скачать

Матричный метод решения систем уравненийСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Элементарные преобразования матриц. Высшая математика.Скачать

13. Метод Гаусса решения систем линейных уравнений. Часть 2.Скачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать








