Элементарные алгебраические функции и уравнения

Видео:A.3.9 Элементарные функции (переснято)Скачать

Классификация элементарных функций

Выделяют множество видов элементарных функций, каждый из которых обладает собственным набором свойств. Так, одни можно дифференцировать на определенном промежутке бесконечное число раз, другие являются непрерывными, ортогональными и др. В этой статье мы расскажем об общепринятой классификации элементарных функций.

Видео:Линейная функция, квадратичная функция и обратно-пропорциональная функция | Математика | TutorOnlineСкачать

Что такое элементарные функции

Начнем с базового определения.

Элементарные функции – это такие функции, которые получаются из основных функций с помощью сложения, вычитания, умножения и деления, а также посредством преобразования сложных функций.

Пример элементарной функции – y = a r c sin 2 x x 2 — 3 + 1 — ln ( x ) .

Таким функции бывают:

В свою очередь алгебраические функции можно разделить на иррациональные и рациональные (целые рациональные и дробные рациональные).

Рассмотрим каждый вид функций отдельно.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Понятие алгебраических функций

Алгебраические функции – это функции, которые состоят из цифр и букв, соединяющихся друг с другом при помощи знаков сложения, вычитания, умножения, деления, извлечения корня и возведения в целую степень.

Иными словами, это те функции, которые можно получить из основных функций f ( x ) = x и f ( x ) = 1 и любых чисел, проведя с ними необходимые алгебраические действия (вычитание, умножение, сложение, деление и др.)

Так, примером алгебраической функции является y = x 2 — 3 4 x .

Выделяют рациональные и иррациональные алгебраические функции.

Рациональные функции – это те, в которых аргумент не находится под знаком корня (радикала). Они в свою очередь делятся на целые рациональные (т.е. многочлены) и дробные рациональные (выражения, составленные из многочленов).

Примером первого вида функций является y = 1 2 x 4 + x — 1 , второго – y = x — a x 3 + b .

Важно отметить, что в рациональных функциях могут присутствовать иррациональные коэффициенты. Основное условие –– отсутствие аргумента функции под знаком радикала. Так, y = 1 3 x 2 — 1 относится не к иррациональным, а к целым рациональным функциям.

Иррациональные функции – это те, которые содержат в себе аргумент под знаком корня (радикала).

Примером такой функции может быть y = x + 1 3 .

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Понятие трансцендентных функций

Прочие функции, которые нельзя отнести к алгебраическим, относятся к виду трансцендентных.

Трансцендентные функции – это те, которые образуются при помощи логарифмирования, возведения в иррациональную степень или с помощью тригонометрических и обратных тригонометрических преобразований.

Пример такой функции – y = log 2 x 3 + 2 3 .

При определении вида функции нужно учитывать один важный момент. Если исходная функция может быть упрощена, то определять вид мы будем уже у полученной в итоге преобразований, а не у исходной функции. Так, y = x 3 + 3 x 2 + 3 x + 1 3 не относится к иррациональным функциям, поскольку при упрощении она становится рациональной y = x 3 + 3 x 2 + 3 x + 1 3 = x + 1 3 2 3 = ( x + 1 ) 2 = x 2 + 2 x + 1 .Функция y = a r c sin ( sin ( 3 x 2 + 1 ) является рационально алгебраической, а не трансцендентной, поскольку y = a r c sin ( sin ( 3 x 2 + 1 ) = 3 x 2 + 1 .

Видео:Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Алгебраические функции

Вы будете перенаправлены на Автор24

Видео:Понятие функции. 7 класс.Скачать

Какими бывают функции?

Чтобы не заблудиться среди огромного разнообразия функций, очень важно выделить признаки той их части, которая называется алгебраическими функциями.

Прежде всего определимся с элементарными функциями.

Любая функция $f$ считается элементарной, если она задана одним уравнением $y=fleft(xright)$, составленным из основных элементарных функций с помощью конечного числа арифметических действий и композиций.

В определении применены следующие понятия:

Это значит, что над двумя данными произвольными функциями $uleft(xright)$ и $vleft(xright)$ в данной области определения можно выполнять сложение $uleft(xright)+vleft(xright)$, вычитание $uleft(xright)-vleft(xright)$, умножение $uleft(xright)cdot vleft(xright)$, а также деление $frac $. При делении предполагается, что для всех $x$ из данной области определения выполняется условие $vleft(xright)ne 0$.

Операция композиции состоит в следующем. Пусть $y$ является функцией от $u$, то есть $y=fleft(uright)$. Пусть также в свою очередь, $u$ является функцией независимой переменной $x$, то есть $u=gleft(xright)$. В этих условиях функция $y=fleft(gleft(xright)right)$ называется композицией данных функций $f$ и $g$.

Функция $y=frac <xcdot 3^> <sqrt> +arcsin ^ x$ является элементарной. В ней использованы все четыре арифметических действия, основные элементарные функции (постоянная, степенная, показательная, тригонометрическая и обратная тригонометрическая), а также представлены композиции функций в виде $arcsin ^ x$ и $sqrt $.

Все элементарные функции распределяют на алгебраические и трансцендентные (те, которые к алгебраическим не относятся).

Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Разновидности алгебраических функций

Существует три основных разновидности алгебраических функций.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Целые рациональные функции (многочлены, полиномы)

Это функции вида $y=Pleft(xright)=a_ cdot x^ +a_ cdot x^ +ldots +a_ cdot x+a_ $, где $a_ ,; a_ ,; ldots ,; a_ $ — постоянные действительные числа, называемые коэффициентами, $n$ — целое неотрицательное число. Если $a_ ne 0$, то $n$ называют степенью многочлена.

Готовые работы на аналогичную тему

Многочлен второй степени $y=3cdot x^ -x+5$. Многочлен нулевой степени $y=7$.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Дробно-рациональные функции (рациональные дроби)

Это функции вида $y=frac =frac <a_cdot x^ +a_ cdot x^ +ldots +a_ cdot x+a_ > <b_cdot x^ +b_ cdot x^ +ldots +b_ cdot x+b_ > $, представляющие собой отношение двух многочленов.

Рациональная дробь $y=frac <x^+1> <7cdot x^+4cdot x-2> $.

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Иррациональные функции

В состав таких функций входят рациональные функции с нецелыми рациональными показателями степени при использовании арифметических действий. Внешний признак иррациональной функции — наличие корней различной степени.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Свойства рациональных дробей

Дана рациональная дробь $frac =frac <a_cdot x^ +a_ cdot x^ +ldots +a_ cdot x+a_ > <b_cdot x^ +b_ cdot x^ +ldots +b_ cdot x+b_ > $, где $Pleft(xright)$ и $Qleft(xright)$ — многочлены. Пусть коэффициенты $a_ ne 0$ и $b_ ne 0$. Тогда указанные многочлены имеют степени $n$ и $m$ соответственно. Данная рациональная дробь определена во всех точках числовой оси, за исключением тех точек, в которых знаменатель $Qleft(xright)=0$.

Рациональную дробь называют правильной, если степень числителя меньше степени знаменателя, то есть $n

Видео:Показательные уравнения. 11 класс.Скачать

Деление рациональных дробей

Если рациональная дробь является неправильной, то посредством деления числителя $Pleft(xright)$ на знаменатель $Qleft(xright)$ её можно представить в виде$frac =Mleft(xright)+frac $ или $Pleft(xright)=Mleft(xright)cdot Qleft(xright)+Rleft(xright)$, где $frac $ — правильная рациональная дробь, а многочлены $Mleft(xright)$ и $Rleft(xright)$ — соответственно частное и остаток от деления многочленов. При этом сумма степеней многочленов $Mleft(xright)$ и $Qleft(xright)$ равна степени многочлена $Pleft(xright)$.

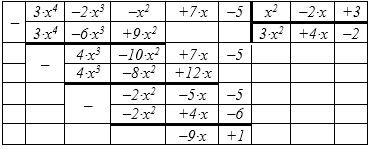
Разделить многочлены $frac <3cdot x^-2cdot x^ -x^ +7cdot x-5> <x^-2cdot x+3> $.

Деление в данном случае возможно, так как степень числителя (четвёртая) больше степени знаменателя (вторая). Деление многочленов выполняем «углом».

Результат деления имеет следующий вид:

[frac <3cdot x^-2cdot x^ -x^ +7cdot x-5> <x^-2cdot x+3> =3cdot x^ +4cdot x-2+frac <x^-2cdot x+3> .] Здесь $Mleft(xright)=3cdot x^ +4cdot x-2$ — частное от деления, $Rleft(xright)=-9cdot x+1$ — остаток от деления.

Видео:Алгебра 7 класс с нуля | Математика | УмскулСкачать

Сокращение рациональных дробей

Рациональная дробь $frac $, как и числовая, бывает сократимой или несократимой. Предположим, что данная рациональная дробь является сократимой, так как оба многочлена $Pleft(xright)$ и $Qleft(xright)$ имеют общие множители, содержащие переменную $x$. Произведение всех этих множителей называется наибольшим общим делителем данных многочленов, то есть $Pleft(xright)=Nleft(xright)cdot P_ left(xright)$ и $Qleft(xright)=Nleft(xright)cdot Q_ left(xright)$, где многочлен $Nleft(xright)$ — наибольший общий делитель. В этом случае данная рациональная дробь приобретает вид $frac =frac <Nleft(xright)cdot P_left(xright)> <Nleft(xright)cdot Q_left(xright)> =frac <P_left(xright)> <Q_left(xright)> $, где рациональная дробь $frac <P_left(xright)> <Q_left(xright)> $ является несократимой, а многочлены $P_ left(xright)$ и $Q_ left(xright)$ называются взаимно простыми. Если многочлен $Nleft(xright)$ — какой-то один наибольший общий делитель, то многочлены $Ccdot Nleft(xright)$, где $C$ — произвольная константа, тоже будут наибольшими общими делителями. Общим делителем взаимно простых многочленов может считаться произвольная константа.

Наибольший общий делитель многочленов $Pleft(xright)$ и $Qleft(xright)$ можно найти с помощью алгоритма Евклида:

1. пусть $Uleft(xright)$ и $Vleft(xright)$ — это новые обозначения многочленов $Pleft(xright)$ и $Qleft(xright)$, причем $Uleft(xright)$ — это тот, который имеет большую степень;
2. делим многочлен $Uleft(xright)$ на многочлен $Vleft(xright)$ и получаем $frac=Mleft(xright)+frac$, где новый многочлен $Pleft(xright)$ представляет собой остаток от деления;
3. обозначаем многочлен $Vleft(xright)$ как $Qleft(xright)$ и возвращаемся на шаг 1.

Выполнение данного алгоритма повторяем, пока на шаге 2 не будет достигнуто нулевое значение остатка от деления $Pleft(xright)=0$. Тогда предпоследний, отличный от нуля остаток от деления, будет наибольшим общим делителем данных многочленов $Pleft(xright)$ и $Qleft(xright)$.

Если полученный по алгоритму Евклида наибольший общий делитель будет иметь вид многочлена $Nleft(xright)$, зависящего от $x$, то данную рациональную дробь $frac $ можно сократить посредством деления и числителя, и знаменателя на $Nleft(xright)$. Если же наибольший общий делитель будет получен в виде константы, то данную рациональную дробь $frac $ следует считать несократимой.

Сначала по алгоритму Евклида находим наибольший общий делитель многочленов $Pleft(xright)$ и $Qleft(xright)$.

Шаг 1. Новые обозначения многочленов $Pleft(xright)$ и $Qleft(xright)$:

[Uleft(xright)=x^ +2cdot x^ -4cdot x-3; Vleft(xright)=x^ +x-6.]

Шаг 2. Результат деления многочленов:

$frac =frac <x^+2cdot x^ -4cdot x-3> <x^+x-6> =x+1+frac <x^+x-6> $, где новый многочлен $Pleft(xright)=x+3$ представляет собой остаток от деления.

Переобозначаем $Qleft(xright)=x^ +x-6$ и возвращаемся на шаг 1.

Шаг 1. Новые обозначения многочленов $Pleft(xright)$ и $Qleft(xright)$:

[Uleft(xright)=x^ +x-6; Vleft(xright)=x+3.]

Шаг 2. Результат деления многочленов: $frac =frac <x^+x-6> =x-2$, где остаток от деления $Pleft(xright)=0$.

Таким образом, наибольший общий делитель — это предыдущий, отличный от нуля остаток, то есть $Nleft(xright)=x+3$. Этот наибольший общий делитель представляет собой многочлен, зависящий от $x$, следовательно, сокращение данной рациональной дроби возможно:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 25 11 2021

Видео:Все графики функций за 20 секундСкачать

Классификация элементарных функций.

Для чего нужно классифицировать элементарные функции?

Ответ очень прост: каждому классу функций соответствует определенный набор свойств. Некоторые функции бесконечное число раз дифференцируемы на каком-либо промежутке, некоторые непрерывны, другие ортогональны с весом и т.д. и т.п.

Согласитесь, когда все книги разложены по полочкам по определенным тематикам, достаточно просто найти нужную.

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Элементарные функции.

Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий (сложение, вычитание, умножение, деление) и образования сложных функций, называются элементарными функциями.

Примером может являться функция .

Очень удобно классификацию элементарных функций представить в виде таблицы.

Элементарные функции

• Трансцендентные
• Алгебраические
  • Иррациональные
  • Рациональные
    • Целые рациональные
    • Дробные рациональные

Итак, по приведенной классификации элементарные функции подразделяются на алгебраические и трансцендентные.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Алгебраические функции.

Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня.

Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты.

Например, функция является алгебраической.

Алгебраические функции подразделяются на рациональные и иррациональные.

Рациональные функции.

Рациональными называются алгебраические функции, которые не содержат аргумент под знаком радикала (корня).

Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов).

Пример целой рациональной функции: .

Пример дробно-рациональной функции: .

Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, — целая рациональная функция, а не иррациональная.

Иррациональные функции.

Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня).

Примером может являться функция .

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Трансцендентные функции.

Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций).

К примеру, — трансцендентная функция.

Если вид элементарной функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция.

К примеру, — не иррациональная функция, а рациональная, так как .

— не трансцендентная функция, а рациональная алгебраическая, так как .

💡 Видео

Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

003. Основные элементарные функции. Начала математического анализаСкачать