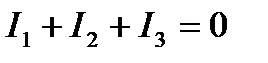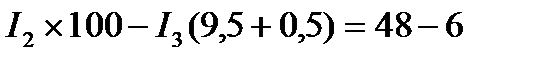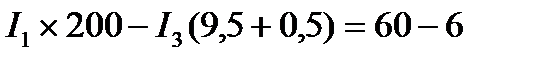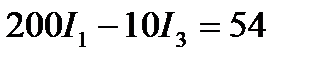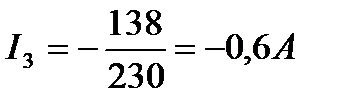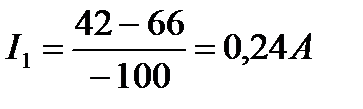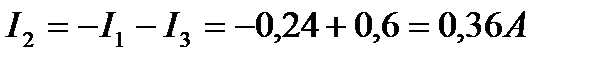Электротехника метод узловых и контурных уравнений

Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.

Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Порядок расчёта:

1. Произвольно задаёмся направлением токов в ветвях.

Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.

Красным выделены изменения после первого действия

Синим выделены изменения после третьего пункта

2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:

1. Обозначаем узлы буквами.
2. Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
   0=I1-I4-I6 (Полученное уравнение)
3. Повторяем пункт B ещё для двух узлов.
   0=-I3+I4+I5(Узел В)
   0=I3-I1-I2(Узел D)

3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы. Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.

3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)

3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)

3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.

Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3

Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5

Контур ABCA 0=I6*R6-I4*R4+I5*R5

4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.

Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.

Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.

I3=I1+I2(Узел D)

I5=I3-I4(Узел В)

I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:

Заменим токи I3 I5 I6 и получим уравнения с тремя токами :

Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:

40 = 71*I1 + 24*I2 + 14*I4

20 = 55*I1 + 93*I2 — 61*I4

0 = 60*I1 + 16*I2 — 81*I4

Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.

Правильность решения можно проверить с помощью баланса мощностей.

Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Метод узловых и контурных уравнений

Данный метод является одним из самых простейших методов расчёта электрических цепей постоянного тока любой сложности. Основывается на составлении уравнений по I и II законам Кирхгофа.

1. Определяем число ветвей m, узлов и контуров в электрической цепи. Число токов в цепи равно числу ветвей. Для каждой ветви выбираем условное направление тока и укажем их на схеме.

2. По первому закону Кирхгофа составляем уравнение для узлов в количестве n-1, где n – число узлов.

3. На основании II закона Кирхгофа составляем m-n+1 уравнений, где m-число ветвей,n-число узлов. Для обхода выбираем контуры с меньшим числом ветвей и содержащих хотя бы одну новую ветвь. Контур обходим по часовой стрелке.

4. Полученные уравнения объединяем в систему и решаем любым способом, известным из математики.

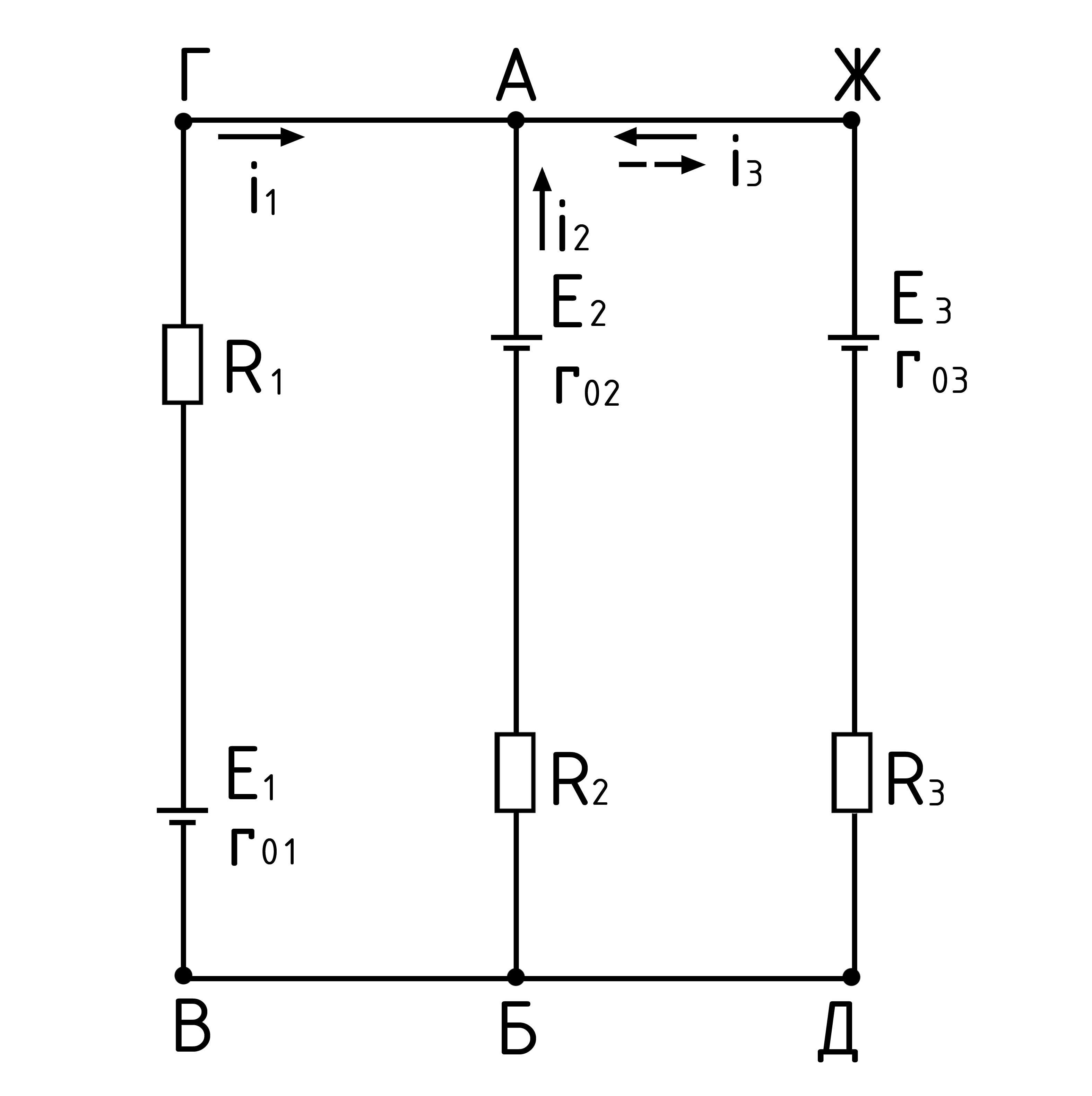
Дано: (рис. 14) Е₁=60 В; Е₂=48 В; Е₃=6 В; R₁=200 Ом; R₂=100 Ом; R₃=9,5 Ом; r₀₃=0,5 Ом; r₀₁=r₀₂ 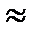0.

1. Сущность метода. Этот метод основан на применении первого и второго закона Кирхгофа, не требует никаких преобразований схемы и пригоден для расчёта любой цепи; в этом его преимущество.

Сколько же нужно составить уравнений для расчёта цепи? Очевидно, столько, сколько неизвестных величин, в нашем случае – токов. Поэтому начнём решение задачи с определения числа неизвестных токов.

2. Определение числа неизвестных токов и выбор их направлений. Как известно, в каждом неразветвлённом участке цепи (ветви) ток имеет одно и тоже значение от начала до конца участка. В рассматриваемой цепи к узловым точкам А и Б присоединены три ветви: БВГА с током I₁, БА с током I₂, БДЖА с током I₃

Итак, число различных токов равно числу ветвей электрической цепи.

Как определить направления токов?

Нам уже известно, что в сложной цепи до её расчёта узнать направления всех токов нельзя. Поэтому в начале направления токов выбирают произвольно (положительные направления токов) и при выбранных направлениях составляют уравнения. Затем решают эти уравнения и определяют истинные направления токов по их алгебраическим знакам, а именно: токи, действительные направления которых обратны выбранным, выражаются отрицательными числами.

Так, в нашем случае можно заранее сказать, что не все выбранные направления токов (рис. 14, сплошные стрелки) совпадают с действительными, так как не могут все токи притекать к узлу А. Очевидно, что один или два тока выразятся отрицательными числами.

Итак, токи в уравнениях Кирхгофа являются алгебраическими величинами, знаки которых зависят от направлений токов.

3. Составление уравнений по законам Кирхгофа. В нашей задаче – три неизвестных тока I₁, I₂, I₃, для определения которых составим три уравнения.

Начнём с уравнений по первому закону Кирхгофа как более простых. Для цепи с n узлами можно составить n-1 независимое уравнение; для одного (любого) узла цепи уравнение не следует составлять, так как оно было бы следствием предыдущих.

В цепи на рис. 14 два узла, поэтому составим одно уравнение по первому закону Кирхгофа, например для узла А:

Два недостающих уравнения составим по второму закону Кирхгофа, выбрав для этого, например, контуры БАЖДБ и ВГЖДВ (чтобы уравнения были независимы, в каждый следующий контур должна входить одна новая ветвь, не входившая в предыдущий).

Приняв обход каждого контура по направлению движения часовой стрелки и учитывая правила знаков, получим:

;

.

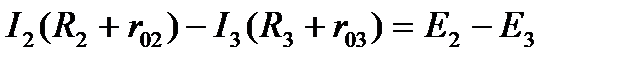
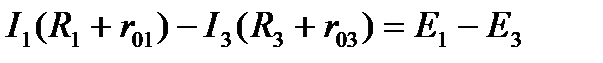
4. Вычисление токов. Подставив в уравнения значения сопротивлений и ЭДС, получим:

Итак, вычисление токов сводится к решению системы трёх уравнений с тремя неизвестными. Для этого, например, определим ток I₂ из уравнения и подставим его значение в уравнение:

;

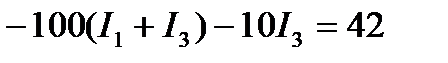
приведя подобные члены, получим:

.

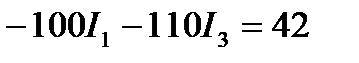
Получились два уравнения с двумя неизвестными: I₁ и I₃.

Умножив второе уравнение на и сложив его с уравнением с первым, получим:

,

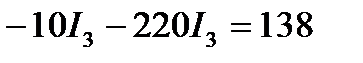
Подставив значение тока I₃ в уравнение , получим:

,

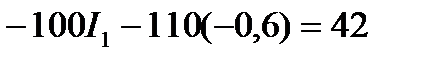
Ток I₂ определим из:

Ток I₁ и I₂ имеют положительные значения, а I₃ – отрицательное, следовательно, направления первых двух токов были выбраны правильно, а тока I₃ – неправильно.

Действительное направление тока I₃ указано пунктирной стрелкой на рис. 14. При этом сумма притекающих к узлу А токов I₁+I₂=0,24+0,36=0,6 А равна оттекающему току I₃=0,6 А.

*Дополнительные вопросы к задаче

1. Сколько электрических контуров имеют цепи, показанные на рис.14 ?

Электрическая цепь (рис.14) имеет три контура: ГАБВГ, ГЖДВГ и АЖДБА. Для составления двух уравнений по второму закону Кирхгофа необходимо и достаточно выбрать два контура. Проще всего выбрать контуры, образующие отдельные ячейки, в нашем случае ГАБВГ и АЖДБА. Число ячеек всегда равно числу независимых уравнений, которые надо составить по второму закону Кирхгофа.

Для расчёта цепи на рис.14 при помощи законов Кирхгофа надо составить пять независимых уравнений (цепь состоит из пяти ветвей). Цепь имеет (А, Б, В), значит, по первому закону Кирхгофа можно составить два независимых уравнения. Недостающие три уравнения нужно составить по второму закону Кирхгофа.

В цепи по рис.14 можно наметить шесть контуров (АВКА, АБВКА, АБМКА, АБВА, АБМВА и БМВБ), но независимые уравнения получаются только для трёх контуров, например для трёх ячеек: АВКА, АБВА, и БМВБ, в каждую из которых входит новая ветвь.

Итак, разветвлённая цепь электрическая цепь имеет больше контуров, чем нужно и можно использовать для составления уравнений.

2. Как вести расчёт, если заданы значения токов, но неизвестны другие параметры цепи?

Очевидно, что из трёх независимых уравнений , составленных для цепи на рис.14 , можно определить любые три неизвестные величины. например, при заданных значениях токов и сопротивлений можно определить ЭДС Е₁, Е₂ и Е₃, а по известным токам и ЭДС – величины трёх сопротивлений.

Итак, порядок расчёта цепи по методу уравнений Кирхгофа не зависит от того, какие величины заданы и какие неизвестны. Число неизвестных величин не должно быть больше числа независимых уравнений, которые можно составить по первому и второму закону Кирхгофа.

3. Следует ли принимать одинаковое направление обхода для всех контуров?

При составлении уравнений было выбрано одно и то же направление обхода этих контуров (по направлению движения часовой стрелки). Приняв для одного из них, например АЖДБА (рис. 14), противоположное направление обхода, получим:

Сравнивая уравнение (4.2) и (4.7), легко убедится, что они тождественны, так как различают только противоположными знаками всех членов уравнения.

Итак, для каждого контура направление обхода может быть выбрано произвольно.

4. Целесообразно ли предыдущую задачу решать методом уравнений Кирхгофа?

Электрическая цепь по рис. 15 имеет пять неизвестных токов, и для их вычисления потребовалась бы пять уравнений (два по первому и три по второму закону Кирхгофа).

Решение системы из пяти не проще, чем вычисление токов в двух простых цепях по методу наложения.

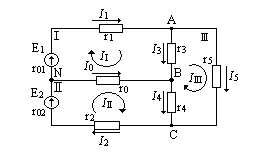
В схеме (рис. 15) трехпроводной линии постоянного тока ЭДС источников Е₁ = 253в и Е₂ = 225в, их внутренние сопротивление r₀₁ = r₀₂ = 0,5 ом, сопротивления главных проводов r₁ = r₂ = 0,5 ом и нейтрального провода r₀ = 1 ом, сопротивления пассивных приемников энергии r₃ = 40 ом, r₄ = 20 ом и r₅ = 40 ом.

Определить токи, применив законы Кирхгофа.

В схеме имеются шесть ветвей и, следовательно, число неизвестных токов равно шести. Число узлов равно четырем.

Намечаем на схеме предполагаемые направления токов в ветвях. После этого составляем, основываясь на первый закон Кирхгофа, три независимых уравнения:

;

;

;

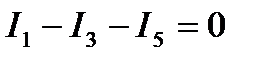
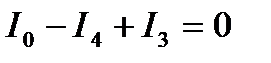
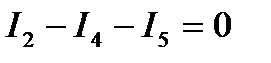
Недостающее уравнение для трех замкнутых контуров I, II и III составляем на основании второго закона Кирхгофа. Направление обхода контуров выбираем по часовой стрелке.

;

;

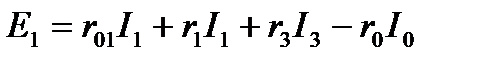
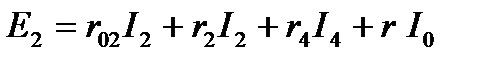
для контура III

.

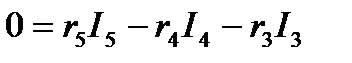
Решение системы уравнений с шестью неизвестными дает: I₃ = 6 a, I₅ = 11 a, I₄ = 10 a, I₂ = 21 a, I₁ = 17 a и I₀ = 4 a.

Найденные токи проверим, подставив их значения в уравнения, составленные на основании первого закона Кирхгофа:

Видео:Метод узловых и контурных уравненийСкачать

Метод узловых и контурных уравнений

Вы будете перенаправлены на Автор24

Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Алгоритм расчета электрической цепи методом контурных и узловых уравнений

Метод узловых и контурных уравнений — самый простой метод расчета электрической цепи, который основан на составлении уравнений по первому и второму законам Кирхгофа.

Первый закон Кирхгофа звучит следующим образом: алгебраическая сумма токов в ветвях цепи, которые сходятся в каждом узле, равна нулю. При этом ток, направленный к узлу считается положительным, а направленный от него отрицательным. Сумма токов, которые направлены к узлу цепи равняется сумме токов, направленных от него. Таким образом получается, что в узел втекает столько же тока, сколько и вытекает из него (правило фундаментального закона сохранения заряда.

Второй закон Кирхгофа гласит — алгебраическая сумма напряжений на резистивных составляющих замкнутого контура цепи равняется сумме электродвижущих сил в составе данного контура. В том случае, когда источник электродвижущей силы отсутствует в контуре, суммарное падение напряжений равно нулю.

Порядок расчета электрической цепи методом узловых и контурных уравнений выглядит следующим образом:

1. Определяют количество неизвестных токов (количество ветвей цепи равняется число токов в ней).
2. Произвольно выбираются направление определенных токов и обозначаются на рассматриваемой схеме.
3. Составляется система уравнений согласно первому закону Кирхгофа, количество которых на единицу меньше количества узлов в рассматриваемой схеме.
4. Составляются недостающие, до общего количества, уравнения по второму закону Кирхгофа. Направления обхода тока, как правило, выбираются одинаковыми.
5. Определяются неизвестные токи, после чего решается получившаяся система уравнений. В том случае, когда рассчитанный (определенный) ток имеет отрицательную величину, это значит, что его направление противоположно направлению, которое было выбрано в пункте 2.
6. Осуществляется проверка посредством составления баланса мощностей или расчет рассматриваемой цепи производится другим методом.

Готовые работы на аналогичную тему

Баланс мощностей электрической цепи — это суммарная генерируемая источниками электроэнергии мощность, равная сумме мощностей, которые потребляются в цепи.

Видео:Лекция 117. Правила КирхгофаСкачать

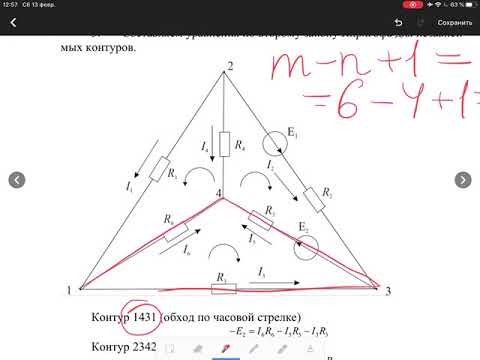
Примеры расчета методом узловых и контурных уравнений

Рассмотрим схему, которая представлена на рисунке ниже

Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ

Допустим, что E1 = 50 В; Е2 = 30 В; Е3=3 В; R1 = 100 Ом; R2 = 50 Ом; R3 = 8 Ом; r03 = 0,5 Ом; r01 = r02 = 0 Ом. Нам необходимо рассчитать все токи цепи.

Решение задачи следует начинать с определения количества неизвестных токов и выбора их направления. В каждом неразветвленном участке цепи (ветвь) электрический ток одно и тоже значение от его начала и до конца. К узловым точкам (А и Б) присоединены три ветви:

1. БВГА с током I1
2. БА с током I2
3. БДЖА с током I3

Таким образом количество разных токов равняется количеству ветвей рассматриваемой цепи. Направление токов выбирается произвольно и при них составляются уравнения. После чего они решаются и определяются их истинные направления (по алгебраическим знакам). В рассматриваемой задаче три неизвестны — I1, I2, I3, для них и составляется система уравнения по законам Кирхгофа. Уравнения на основе первого закона более простые, поэтому следует начинать с них. Известно, что для электрической цепи с n узлами можно составить n-1 независимых уравнений. Уравнение по первому закону Кирхгофа для узла А будет выглядеть следующим образом:

Уравнения, которых не хватает составляются по второму закону Кирхгофа. Для этого выбираем контуры БАЖДБ и ВГЖДВ. Принимаем, что обход контуров цепи осуществляется по часовой стрелке и учитывая правила знаков получаем следующие уравнения:

Подставив численные значения в третьем уравнение получаем:

$I1*(100+0) – I3*(8+0,5) = 50-30$

Таким образом вычисление токов сводится к решению системы из трех уравнений с тремя неизвестными. Рассчитаем I2 из уравнения и подставим значение в уравнение:

$-50*(I1+I3) – 8,5*I3 = 27$

Приводя подобные числа получим:

В результате у нас получилось два уравнения с двумя неизвестными (I1, I3). Уравнение (-50I1-58,5I3 = 27) умножается на два, в результате чего получается:

$-100*I1- 117*I3 = 54$ Получившееся уравнение складывается с уравнение (100I1-8,5I3 = 20):

$I3 = — (64/125,5) =- 0,5 A$

Теперь подставляем получившееся значение I3 в уравнение, где неизвестно I1:

$I1 = -24,5/-100 = 0,245A$

Теперь получившиеся значения подставляются в первое уравнение, составленное по первому закону Кирхгофа:

$I2 = 0,245+0,5 = 0,745A$

Проверка результата осуществляет при помощи составления баланса мощностей или решения задачи другим способом.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 08 2021

Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет

🔥 Видео

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать

Электротехника (ТОЭ). Лекция 4. Метод контурных токов | Решение задачСкачать

Метод контурных токовСкачать

Правила Кирхгофа - определение токов. ЭлектротехникаСкачать

Законы Кирхгофа. Метод контурных токов (МКТ)Скачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

МКТ │Цепь с источниками тока │Расчет цепи методом контурных токовСкачать

1 4 3 Метод узловых напряжениеСкачать

Электротехника. Метод узловых потенциалов.Я в вк https://vk.com/id4682924Скачать

46 Алгоритм решения метода узловых и контурных уравненийСкачать

Правила Кирхгофа, метод контурных токов и узловых потенциаловСкачать

Электротехника (ТОЭ). Лекция 5. Метод узловых потенциалов | Решение задачСкачать