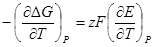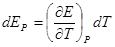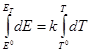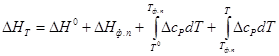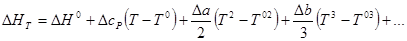Изменение энергии Гиббса для реакции, обратимо протекающей в гальваническом элементе, можно записать
Запишем также уравнение Гиббса — Гельмгольца
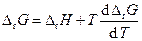
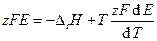
Учитывая, что для химической реакции справедливо
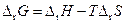
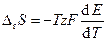
Таким образом, температурный коэффициент ЭДС связан с изменением энтропии химической реакции, протекающей в гальваническом элементе.
На практике, измеряя ЭДС гальванического элемента при разных температурах и постоянном давлении, мы можем определить как изменение энтропии, так и изменение энтальпии соответствующей химической реакции.
Потенциометрия
Потенциометрия — метод исследования, в основе которого лежат термодинамические соотношения между ЭДС электрохимических цепей, с одной стороны, и физико-химическими параметрами растворов и химических реакций с другой. Потенциометрию используют для определения
— констант гидролиза солей,
— констант диссоциации кислот и оснований,
— произведений растворимости малорастворимых соединений,
— констант устойчивости комплексов,
— коэффициентов активности ионов в растворах,
— термодинамических характеристик химических реакций
Например, ионное равновесие в растворе характеризуется соответствующими термодинамическими константами. Например, для малорастворимого соединения, диссоциирующего по уравнению
AB 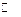
равновесие характеризуется произведением растворимости:
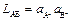
Для определения произведения растворимости можно составить гальванический элемент
A | AB | DB || AC | A,
где AC и DB — хорошо растворимые соли соответствующего катиона (A + ) и аниона (B – ), A + | A — электрод первого рода, а B – | AB, A — электрод второго рода. На электродах будут протекать следующие реакции:
(1) A + + e – 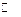
(2) AB + e – 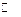
Запишем уравнения Нернста для этих электродов.
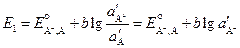
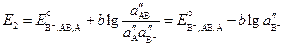
Электрод второго рода можно представить как электрод первого рода, только с очень малой концентрацией иона металла, которая будет зависеть от концентрации аниона, образующего с ним малорастворимое соединение. Тогда, учитывая выражение для произведения растворимости, получим
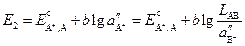
Выражение для ЭДС этого элемента будет
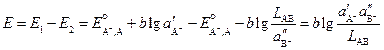
Таким образом, произведение растворимости малорастворимого соединения связано с ЭДС рассмотренного элемента, и для его определения необходимо измерить ЭДС элемента при известных активностях иона металла (A + ) в растворе первого электрода и аниона B – в растворе второго.
Для определения других термодинамических констант необходимо составлять соответствующие электрохимические цепи и измеряя их ЭДС при известных активностях потенциалопределяющих веществ вычислять значение констант.
Рассмотрим, например, как методом потенциометрии можно оценить термодинамические функции химических реакций 
1) изменение энергии Гиббса:
2) изменение энергии Гельмгольца:
DA = — zFE — Dn RT, (3.57)
где Dn – изменение числа молей газообразных веществ, участвующих в реакции;
3) изменение энтропии можно оценить, зная зависимость ЭДС элемента от температуры:
DS= zF 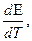
где 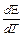
Например, зависимость ЭДС от температуры можно описать уравнением:
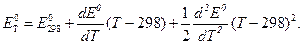
При изменении температуры ЭДС элемента может оставаться постоянной величиной, увеличиваться или уменьшаться в зависимости от величины и знака температурного коэффициента ЭДС.
4) изменение внутренней энергии системы:
DU = Qv = — zF (E-T 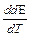
5) тепловой эффект химической реакции:
DH = Qp = — zF(E — T 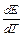
Если реакция в элементе протекает без выделения газов, то можно принять, что
Приведённые выше выражения можно использовать и для вычисления стандартных величин (DG° , DA°, DS°, DH°, DU°).
Если стандартные термодинамические потенциалы определяются по справочным данным, то возможно решение обратной задачи, то есть определение стандартной ЭДС. При этом используются соотношения:
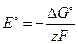
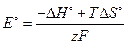
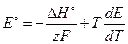
Видео:Первый закон термодинамики. 10 класс.Скачать

ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМ
При обратимом протекании в системе какого-нибудь процесса в изотермических условиях и при постоянном давлении связь между изменением энергии Гиббса (ΔG), энтальпии (ΔН) и энтропии (ΔS) дается уравнением
в котором TΔS есть изменение связанной энергии системы. При этом система представляется настолько большой, что переход ее от начального состояния к конечному не вызовет заметного изменения параметров. Например, в системе с химической реакцией начальные и конечные концентрации участников реакции можно считать одними и теми же. Если в системе идет процесс перехода вещества от большей концентрации к меньшей, то эти изменения происходят на бесконечно малую величину и т. д. Из термодинамики известно, что
Это уравнение принято называть уравнением Гиббса — Гельм-гольца. Убыль энергии Гиббса электрохимической системы равна максимальной работе ΔА, которую может совершить система, а эта максимальная электрическая работа равна произведению напряжения системы на количество прошедшего электричества, т. е. zFE. Таким образом:
Продифференцируем это выражение по температуре:
Следовательно, изменение энтропии можно определить из температурного коэффициента напряжения системы.
Подставив в уравнение Гиббса — Гельмгольца выражение убыли энергии Гиббса, получим
Так как изотермическая и обратимая электрическая работа является полным дифференциалом параметров Р, Т, то
и если Р = const, то
и полученное уравнение переписываем в виде:
В этом уравнении ΔН относится к количеству вещества, вступившему в реакцию при прохождении zF количества электричества, т. е. к одному молю.
Совершенно аналогичное выражение получается, если процесс идет изотермически и обратимо, но не при постоянном давлении, а при постоянном объеме. Тогда

Электрическая работа, совершаемая системой, может быть больше, меньше или равна изменению энтальпии в зависимости от знака температурного коэффициента напряжения. Если (dE/dT)P = 0, то
и электрическая работа точно равна изменению энтальпии. Это уравнение называется уравнением Томсона. Его иногда применяют для ориентировочных расчетов напряжения.
Если (dE/dT)P > 0, то электрическая работа больше изменения энтальпии и электрохимическая система в обратимом изотермическом режиме превращает в электрическую работу не только энергию, выделяющуюся при уменьшении энтальпии процесса, но и часть энергии окружающей среды. В адиабатическом режиме система, следовательно, будет охлаждаться.
В качестве примеров рассмотрим несколько электрохимических систем с водными и расплавленными электролитами (табл. 6.4).
Таблица 6.4. Проверка уравнения Гиббса — Гельмгольца
| № по пор. | Электрохимическая система | Химическая реакция в системе |
| 1. 2. 3. 4. 5. | (–) Zn | ZnCl2 (aq), AgCl (тв.) | Ag (+) 0,535 кмоль/м 3 (–) Pb | (CH3COO)2Pb (aq) || || (CH3COO)2Cu (aq) | Cu (+) (–) Hg | HgO, KOH || KCl, Hg2Cl2 | Hg (+) 0,01 кмоль/м 3 0,01 кмоль/м 3 (–) Pb | PbBr2 (расплав) | Br2 (C) (+) (–) Ag | AgCl (расплав) | Cl2 (C) (+) | Zn + 2AgCl (тв.) = = ZnCl2 + 2Ag Pb + (CH3COO)2Cu = = (CH3COO)2Pb + Cu Hg2Cl2 + 2KOH = = Hg2O + H2O + 2KCl Pb + Br2 = PbBr2 Ag + ½ Cl2 = AgCl |
Система 1 обладает отрицательным температурным коэффициентом, и реакция в ней протекает с уменьшением энтальпии (экзотермическая реакция), которая из термохимических данных в условиях протекания реакции равна — 218,0 кДж/моль. Электрическая работа, которую может совершить система, меньше, чем ΔН. Расчет по формуле дает значение изменения энтальпии системы, очень близкое к определенному из термохимических измерений. В рассматриваемой электрохимической системе 90% выделяемой теплоты расходуется на совершение электрической работы, а 10% рассеивается или нагревает систему. Аналогичные соотношения имеем и для систем 4, 5. Рассчитанные из электрохимических измерений значения энтальпии совпадают с термохимическими данными в пределах ошибок опыта, а в электрическую работу превращается соответственно 73 и 82% от выделяющейся теплоты.
Температурный коэффициент напряжения системы 2 положителен. В соответствии с этим в электрическую работу превращается не только вся теплота, выделяющаяся при протекании реакции, но и часть теплоты (примерно 33%), поглощенной из окружающей среды. Значения энтальпии, определенные из электрохимических и термохимических измерений, хорошо согласуются друг с другом.
Наконец, в электрохимической системе 3 положителен не только температурный коэффициент напряжения, но и изменение энтальпии. Следовательно, эта система отбирает тепловую энергию от внешней среды не только для совершения электрической работы, но и на химическую реакцию.
Данные, приведенные в табл. 6.4, относятся к реакциям, протекающим не при стандартной температуре (298,15 К или 25°С). Для стандартных условий уравнение Гиббса — Гельмгольца должно быть записано в виде:
| Т, К | z | E, B |  , В/град , В/град | ΔG,  | 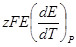 , ,  | ΔН, кДж/моль |
| из изме-рения напря-жения | из тер-мохи-мичес-ких данных | |||||
| 1,015 0,476 0,164 1,100 0,913 | – 4,02∙10 –4 3,85∙10 –4 0,84∙10 –3 – 0,67∙10 –3 – 0,29∙10 –3 | – 196,0 – 92,0 – 31,6 – 212,6 – 88,1 | – 21,0 21,8 46,7 – 79,0 – 20,4 | – 217,0 – 70,2 15,1 – 291,6 – 108,5 | – 218,0 – 69,1 15,7 – 289,1 – 106,8 |
Здесь Е°, ΔН°, Т°, dE°/dT — величины, относящиеся к стандартным условиям.
Если же необходимо провести расчеты при каких-нибудь условиях, отличных от стандартных, то нужно знать ΔН и dE/dTдля этих условий. Рассмотрим сперва зависимости этих величин от температуры, считая, что активности участников реакции при всех температурах равны единице,
Вообще говоря, температурный коэффициент напряжения может изменяться с температурой, а также оставаться постоянным в значительном температурном интервале. Характер его изменения будет определяться изменением напряжения с температурой.
Продифференцируем уравнение Гиббса — Гельмгольца по температуре:
Из этого выражения следует, что
и если напряжение системы не зависит от температуры или линейно зависит от нее, то (∂ 2 Е/∂∂Т 2 )Р =0 и тогда
Но в соответствии с уравнением Кирхгоффа
где 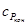

Следовательно, для соблюдения условий независимости или линейного хода Е с температурой нужно, чтобы при протеканиипроцесса не происходило бы изменения теплоемкости системы, т. е. чтобы ΔсР = 0. Тогда изменение напряжения с температурой будет происходить только вследствие изменения энтропии системы.
В рассматриваемом случае, поскольку изменение энтальпии не зависит от температуры, можно легко определить значение Е для любой температуры (Ет), если только линейный ход Е с температурой соблюдается вплоть до этой температуры. Из выражения
Ет = Е 0 + k (Т – Т 0 )
где k — положительное или отрицательное значение температурного коэффициента.
Если же температурный ход напряжения системы не линейный, то напряжение системы определяется следующим образом. Определим изменение энтальпии при температуре Т(ΔНТ) интегрированием уравнения Кирхгоффа:
В случае какого-либо фазового превращения в системе в данном интервале температур нужно учесть также изменение энтальпии при этом превращении (ΔНф. п), т. е.
Теперь задача определения ΔНТ может быть решена, если известен температурный ход теплоемкости каждого из участников реакции. В ряде случаев ход теплоемкости с температурой может быть выражен в виде ряда:
Тогда для ΔсР аналогично
ΔсР = ΔсРº + ΔаТ + ΔbT 2 + ΔcT 3 + …
Подставив это выражение в уравнение для ΔНТ и проинтегрировав его в пределах от T 0 до Т, получим:
При наличии в системе фазовых превращений ход рассуждений остается тем же, нужно только воспользоваться формулой для ΔНТ, где учтено изменение энтальпии при фазовых превращениях.
Определение температурного коэффициента напряжения при температуре Т можно провести, воспользовавшись соотношением
из которого следует, что
Подставив вместо ΔсР степенную зависимость и проведя интегрирование, окончательно получим изменение энтропии системы при интересующей нас температуре:
Разделив теперь ΔST на zF, получим температурный коэффициент и с помощью формулы Гиббса — Гельмгольца определим напряжение системы ЕT. Следует помнить, что ЕT относится к температуре Т и активностям участников реакции, равным единице.
Когда в реакции, протекающей в электрохимической системе, имеются газообразные участники, напряжение системы оказывается зависящим от давления. Для определения напряжения как функции давления (ЕР) следует воспользоваться термодинамическим соотношением
где V — изменение мольного объема при реакции.
Так как ΔGV = – zFE, то
Интегрирование этого выражения дает:
Если изменение объема подчиняется уравнению состояния идеального газа, то
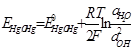
Здесь ЕP — напряжение системы при давлении Р, стандартной температуре и активностях всех конденсированных участников реакции, равных единице.
Если конденсированные участники реакции находятся не в стандартных состояниях, то это обстоятельство должно быть учтено при расчетах, но такие расчеты выходят за рамки книги.
Рассмотрим теперь формулу Гиббса — Гельмгольца применительно к системам без химической реакции.
В системах с электродами из разных модификаций одного и того же металла, например в системе
Sn (белое) | SnSO4 | Sn (серое)
ΔH – изменение энтальпии при аллотропном переходе серого олова в белое. При температуре, отвечающей равновесию обеих модификаций, ΔG = 0 и, следовательно, Е = 0, откуда
т. е. все изменение энтальпии эквивалентно изменению связанной энергии системы.
Аналогичные рассуждения можно применить и к системам типа
М (жидкий) | Расплавленная соль | М (твердый)
(где М — металл), например
при температуре плавления. Поскольку при плавлении энтальпия изменяется, то, на первый взгляд, можно было ожидать, что при замыкании такой системы потечет ток и произойдут процессы растворения жидкого металла и восстановления ионов металла на твердом электроде. Однако такое заключение ошибочно, ибо при температуре плавления ΔG = 0 и вся теплота, затрачиваемая на плавление, идет на увеличение связанной энергии системы. Следовательно, в этом случае напряжение системы равно нулю и она не может совершить работы.
В остальных типах систем без химической реакции никаких превращений не происходит, а электрическая работа совершается в результате переноса энергии от более высокого уровня к менее высокому уровню. Поскольку в случае идеальных систем внутренняя энергия U не зависит от объема, то ΔH = 0 и
Следовательно, электрическая работа в таких системах совершается только вследствие изменения связанной энергии. Преобразовав это уравнение
откуда после интегрирования имеем
ln E = ln Т + const и E = k’T
В идеальных электрохимических системах данного типа напряжение, таким образом, прямо пропорционально абсолютной температуре.
В реальных же системах (∂U/∂V)P ≠ 0 и ΔH в формуле Гиббса — Гельмгольца будет равно энтальпии перехода моля вещества от уровня с большей энергией на уровень с меньшей энергией. Например, в системах типа
ΔH — изменение энтальпии при переходе моля растворенного электролита от активности а2 к активности а1, т. е. энтальпия разведения в данных пределах (а2 > a1).
В указанного типа электрохимической системе не всегда удается достаточно полно элиминировать скачок потенциала на границе двух жидких фаз. Поэтому удобнее воспользоваться двумя одинаковыми электрохимическими системами с химическими реакциями, в одной из которых активность электролита равна а1, а в другой — a2, и включить их в измерительную цепь напротив друг другу таким образом, чтобы слева находилась система с большим напряжением:
(–) (Pt) H2 | HCl, AgCl (тв.) | Ag — Ag | AgCl (тв.), НС1 | H2 (Pt) (+)
Измеренное напряжение Ep = E1 – E2 и, следовательно,
При небольших разностях концентраций разность температурных коэффициентов очень невелика, и таким путем из измерений напряжения можно прямо рассчитать энтальпию разведения от активности а2 до а1.
Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Термодинамика электрохимических процессов. Электродвижущие силы. Электродные потенциалы
Утверждено редакционно-издательским советом. Тюменского Государственного Нефтегазового Университета
Составители: — заведующий кафедрой физической и аналитической химии, доктор химических наук, профессор;
© Тюменский Государственный Нефтегазовый Университет, 2000 г.
1. Термодинамика электрохимических процессов. Электродвижущие силы. Электродные потенциалы.
1.1. Термодинамика электрохимического элемента.
Рассмотрим, что такое электрохимический элемент. Превращение химической энергии в электрохимическую возможно в гальваническом элементе. Гальванический элемент — это устройство, позволяющее получать электрический ток за счет протекания химической реакции.
За некоторым исключением реакцию можно провести обычным химическим путем или в гальваническом элементе. Например, реакцию взаимодействия:
можно реализовать опустив цинковую пластинку в раствор сульфата меди. При этом, эта реакция будет протекать химическим путем. Эту же реакцию можно реализовать в гальваническом элементе, изображенном на рис. 1.1.
Рис. 1.1. Медноцинковый гальванический элемент. 1 — сосуд; 2 — цинковый электрод; 3 — медный электрод; 4 — полупроницаемая перегородка;
5 — соединительный провод.
На электродах и в гальваническом элементе будут протекать следующие процессы:

на отрицательном полюсе (-)
суммарная реакция в элементе
Путь реакции, реализуемой в гальваническом элементе, называется электрохимическим. При реализации реакции химическим путем электроны непосредственно передаются от металлического цинка иону меди. При реализации реакции электрохимическим путем электроны от металлического цинка передаются иону меди по проводнику. В основе всякой гальванической цепи лежит окислительно-восстановительная
реакция, которая протекает таким образом, что окисление происходит на одном полюсе(отрицательном), а восстановление на другом полюсе(положительном).
Растворы сульфата меди и сульфата цинка во избежание их перемешивания разделены полупроницаемой перегородкой.
Изображенный на рис. 1.1. гальванический элемент записывается следующим образом:
Если электроды соединить металлическим проводником, то происходит растворение цинкового электрода. Катионы цинка переходят в раствор, а электрод при этом заряжается отрицательно; катионы меди разряжаются на медном электроде. По внешнему металлическому проводнику поток электронов переходит с цинкового электрода на медный, давая электрический ток. Медный электрод служит положительным полюсом элемента, а цинковый — отрицательным. Между отрицательным и положительным полюсами возникает разность потенциалов. Если гальванический элемент работает в термодинамически обратимых условиях, то эта разность потенциалов будет максимальной и она называется электродвижущей силой элемента (ЭДС).
Если активности веществ, участвующих в электродных процессах, равны единице, то возникающая при этом ЭДС называется стандартной ЭДС (Еº).
Для обратимо работающего гальванического элемента (при Р=сопst и Т’=сопst) будем иметь:
где А т’ -максимально полезная работа гальванического элемента; ΔG — изменение энергии Гиббса для реакции, протекающей в гальваническом элементе; Е — электродвижущая сила элемента.
Изменение энтропии для любого процесса определяется уравнением:

Берем дифференциал от уравнения (1.4) по температуре:

Подставляя уравнение (1.6) в уравнение (1.5) получим:

Теперь найдем значение ΔН реакции, протекающей в гальваническом элементе. Из термодинамики известно уравнение:
Подставляем уравнения (1.4) и (1.7) в уравнение (1.8) и получаем:

Связь между стандартной ЭДС и константой равновесия (К,) реакции, протекающей в гальваническом элементе, можно найти воспользовавшись уравнением изотермы химической реакции:

Из уравнения (1.10) следует:

Если 
Из уравнения (1.11) в этом случае получаем:

1.2. Электродные потенциалы.
Для рассмотрения понятия электродного потенциала рассмотрим два примера.
1-ый пример. Пусть имеется насыщенный раствор сахара:
Химический потенциал сахара в растворе 
твердого сахара 




2-ой пример. Медная пластинка опущена в раствор сульфата меди. На ней протекает процесс 



отрицательно заряженных ионов 





Рис. 1.2 Схема образования двойного
Таким образом, в системе образуется двойной электрический слой. Этот слой подобен конденсатору и в нем возникает скачок потенциала, который и называется электродным потенциалом.
Ионы меди при выделении должны преодолеть двойной электрический слой, т. е. они должны совершить работу против электрических сил двойного электрического слоя. Условием равновесия в системе будет:

где (р -равновесный электродный потенциал. Таким образом, равновесие между раствором электролита и электродом устанавливается тогда, когда работа перенесения одного грамм-иона из раствора в металл, равная разности химических потенциалов ионов в растворе и атомов в металле, станет равной работе против электрических сил в двойном электрическом слое.
Равновесный электродный потенциал зависит от активности реагентов, участвующих в электродном процессе. Для нахождения этой зависимости воспользуемся уравнением для химического потенциала:

где μ-стандартный химический потенциал; а — активность реагента. Запишем уравнение (1.14) для иона (окисленная форма) и металла (восстановленная форма вещества):


где 

Если 


приведется к виду:

где φº-стандартный электродный потенциал.
Между ЭДС гальванического элемента и электродным потенциалом существует связь: .

где 
Опытным путем нельзя определить абсолютную величину электродного потенциала; можно определить только величину ЭДС. Поэтому условились считать равной нулю величину стандартного водородного электрода, т. е. величину потенциала водородного электрода при 

(+) 

ЭДС этой гальванической цепи равна:
Таким образом, численное значение электродного потенциала равно ЭДС гальванического элемента, составленного из данного электрода и стандартного водородного электрода.
Электродному потенциалу электрода приписывают знак, одинаковый со знаком полюса элемента, составленного из этого электрода и стандартного водородного электрода.
Величины стандартных равновесных электродных потенциалов были определены опытным путем для большинства металлов. Если расположить величины стандартных равновесных электродных потенциалов в порядке возрастания их алгебраических величин, то получится ряд напряжений:
Электрод: 



φº , B: -3.045; -2.714; -0.763; -0.126


0,00; +0,521; +0,729; +1,360
Отрицательный стандартный потенциал имеют электроды, которые по отношению к стандартному водородному электроду заряжаются отрицательно, т. е. на этом электроде при работе соответствующего гальванического элемента атомы переходят в раствор. Переход же ионов из раствора в металл осуществляется только путем электролиза. Положительный стандартный потенциал имеют электроды, которые по отношению к стандартному водородному электроду заряжаются
положительно, т. е. при работе соответствующего гальванического элемента ионы металла переходят из раствора в металл.
Знак заряда электрода, входящего в ту или иную гальваническую цепь, по отношению к другому электроду этой цепи может и не совпадать со знаком заряда в ряду напряжений, т. к. этот знак зависит от вида другого электрода в элементе. Например, в гальваническом элементе, составленном из свинцового и медного электродов, свинцовый электрод будет электроотрицательным полюсом, а в гальваническом элементе, составленном из цинкового и свинцового электродов, свинцовый электрод будет электроположительным полюсом.
1.3. Типы и виды электродов.
Электроды, изготовленные из металла, погруженного в раствор его ионов,’ работают на основе обмена катионами между электродом и раствором. Такие электроды называются электродами обратимыми относительно катиона. На них протекает электродная реакция:
На таком электроде реакция протекает слева направо, если электрод более отрицателен, чем второй электрод, соединенный с ним, и справа налево, если его потенциал более положителен, чем потенциал второго электрода. Для такого электрода уравнение для потенциала имеет вид:

где 
Для металла 

Существуют также электроды обратимо обменивающиеся с раствором анионами. Также электроды называются обратимыми относительно аниона. Примером такого электрода может служить йодный электрод, изготовленный из платины, покрытой йодом, и погруженный в раствор, содержащий 
Она протекает слева направо, если электрод отрицателен относительно второго электрода, и справа налево, если он положителен относительно второго электрода. Для таких электродов

Различают электроды 1-го и 2-го рода. Электродами 1-го рода называются системы, в которых концентрация ионов в растворе, относительно которых обратим электрод, может быть различной, а электродами 2-го рода называются системы, в которых эта концентрация постоянна, так как в электродах применяются насыщенные растворы. Электроды 2-го рода построены из металла, покрытого малорастворимой его солью, погруженного в раствор какой-нибудь легко растворимой соли с тем же анионом. Примером такого электрода может служить хлорсеребряный электрод:
В таком электроде идет обратимая реакция образования AgCl из Аg-электрода и Сl¯раствора:
Потенциал этого электрода будет:


где Пр — произведение растворимости АgС1.
Электроды 2-го рода отличаются хорошей воспроизводимостью, большим постоянством и легко могут быть изготовлены. Поэтому их часто применяют в качестве эталонных электродов вместо водородного электрода.
Существуют также электроды, которые не обмениваются с раствором ни катионом, ни анионом, а лишь обеспечивают подвод электронов для окислительно-восстановительной реакции, протекающей на границе электрод-раствор. Такие электроды называются окислительно-восстановительными. Примером такого электрода может служить электрод, состоящий из платины, погруженной в раствор, содержащий ионы Fе2+ и Fе3+ На таком электроде протекает реакция:
Fе3+ +e↔ Fе2+ Уравнение для потенциала электрода имеет вид:

Своеобразную группу составляют газовые электроды, в которых проводник из металла (Pt, Jr, Au) погруженного в раствор, непрерывно насыщается газом, который вступает в обмен с ионами раствора. Газовые
электроды могут быть обратимыми как относительно катиона (водородный электрод), так и аниона (хлорный электрод).
1.4. Основные типы гальванических цепей.
Различают химические и концентрационные гальванические цепи. Электрохимическая система, работающая за счет осуществления химической реакции называется химической цепью.
Различают химические цепи с двумя и одним электролитом. К электрохимическим цепям с двумя электролитами относится элемент Якоби-Даниэля:
На электродах этого элемента протекают следующие реакции:
Суммарная реакция, протекающая в гальваническом элементе, следующая:
ЭДС этого, гальванического элемента будет определяться уравнением:

Уравнение (1.26) с учетом уравнения (1.27) запишется в следующем виде:

Примером химической цепи с одним электролитом может быть цепь:
(+) 
Электродные и суммарная реакция в этом гальваническом элементе будут следующие:
(+)
(-)
Потенциалы электродов и ЭДС этого гальванического элемента будут описываться следующими уравнениями:


где
Из приведенных гальванических цепей видно, что в химических цепях электроды отличаются химическими свойствами.
Концентрационными гальваническими элементами называются элементы, в которых оба электрода одинаковы по своей природе, но различаются активностью растворов или металла электрода. Электрическая энергия в этих элементах получается за счет выравнивания концентраций веществ в элементе.
Концентрационные элементы могут быть без переноса и с переносом. Концентрационными элементами без переноса являются следующие элементы: а) с одинаковыми электродами и двумя одинаковыми по природе, но различными по концентрации растворами электролитов, причем между растворами отсутствует непосредственное соприкосновение; б) с электродами из двух сплавов, одинаковых по природе, но различных по концентрации (с одним раствором электролита);
в) с газовыми электродами, одинаковыми по природе, но с различными давлениями газа на электродах (с одним раствором электролита).
Примером концентрационного элемента без переноса с одинаковыми, электродами и с двумя одинаковыми электролитами разной концентрации служит элемент:
(+) 

где


(+)
Электрическая энергия в рассматриваемом гальваническом элементе получается за счет выравнивания концентраций 2пС1^ в правой и левой частях гальванического элемента. ЭДС этого элемента определяется уравнением:
где 
Примером концентрационной цепи с разными концентрациями металла электрода может служить элемент:
(+) 

где 

(+)
(-)
ЭДС этого концентрационного элемента получается за счет выравнивания активности кадмия в обеих амальгамах.
Уравнения для электродных потенциалов и для ЭДС этого элемента следующие:



Примером газового концентрационного элемента может служить элемент:
(+) 

Электродные и суммарная реакции в этом гальваническом элементе следующие:
(+)
(-)
ЭДС газового концентрационного элемента без переноса получается за счет выравнивания давления водорода на обоих электродах
Уравнения для потенциалов электродов и ЭДС этого элемента имеют вид:



Концентрационной цепью с переносом является гальванический элемент с двумя одинаковыми электродами и с двумя растворами одинаковых электролитов, но разной концентрации, при этом между обоими растворами имеется жидкостный контакт. В этом жидкостном контакте возникает диффузионный скачок потенциала (
Концентрационный элемент с переносом может быть составлен из электродов 1-го рода и электродов 2-го рода. Примером элемента, составленного из электродов 1-го рода, может быть следующий гальванический элемент:
(+) 


Суммарным процессом концентрационной цепи с переносом является только перенос электролита из одного раствора в другой в процессе диффузии через жидкостную границу.
ЭДС этого элемента будет равна:

где 
Электрическая энергия в этом элементе получается за счет диффузии электролита из раствора с большей концентрацией в раствор с меньшей концентрацией, при этом переход ионов электролита происходит непосредственно через жидкостную границу за счет диффузии в отличие от цепей без переноса.
Уравнение (1.40) для рассматриваемого гальванического элемента можно привести к виду:

Из уравнения (1.41) видно, что если оба электрода концентрационной цепи с переносом обратимы относительно катиона, то в выражении для ЭДС множителем входит число переноса аниона, при этом в пространстве положительного полюса концентрация электролита больше, чем в пространстве отрицательного полюса.
Примером концентрационной цепи с переносом с электродами 2-го рода является цепь:


ЭДС этой гальванической цепи определяется уравнением:

Из уравнения (1.42) следует, что если оба электрода концентрационной цепи с переносом обратимы относительно аниона, то в уравнении для ЭДС входит множителем число переноса катиона, при этом концентрация в пространстве положительного полюса меньше, чем в пространстве отрицательного полюса.
В гальванической цепи с переносом на границе двух растворов электролитов возникает разность потенциалов, которая называется диффузионным потенциалом. Растворы могут различаться природой и концентрацией электролитов. В общем случае уравнения для вычисления диффузионного потенциала получаются сложными. Рассмотрим два частных случая: а) диффузионный потенциал на границе растворов двух одинаковых электролитов, но разной концентрации; б) диффузионный потенциал на границе двух растворов электролитов одинаковой концентрации, но различающихся одним из ионов.
Для первого случая границу двух растворов электролитов можно представить как НС1\НС1.

Пусть 

 |  |
Подвижность ионов водорода больше подвижности хлорид — иона и, следовательно, с правой стороны границы будет возникать больший положительный заряд, чем с левой стороны и возникает двойной электрический слой. В двойном слое возникает скачок потенциала, который и является диффузионным потенциалом. Таким образом, причина возникновения 
Уравнение для вычисления диффузионного потенциала можно вывести используя уравнения( 1.40), (1.41) и (1.33):
Из уравнения (1.40) можно получить:


Из уравнения (1.33) следует:

Из уравнения (1.41):

Подставляем (1.44) и (1.45) в (1.43) и получаем:




Из уравнения (1.48) следует, что если 


Границу раздела двух растворов электролитов одинаковой концентрации, но различающихся одним из ионов можно представить следующим образом :NаС1\КС1.
Ионы 


избыток ионов калия. В результате этого с левой стороны граница будет иметь избыток положительного заряда, а с правой — избыток отрицательного заряда. Образуется двойной электрический слой, в котором возникает скачок потенциала — диффузионный потенциал. Уравнение для вычисления Ме
При этом ионы металла будут с поверхности металла забирать электроны. В результате этого граница раздела металла и раствора со стороны металла будет заряжаться положительно, а со стороны раствора — отрицательно (рис.2.2). В обоих случаях на границе раздела металл-раствор возникает двойной электрический слой, который называется ионным двойным электрическим слоем.
2. Двойной электрический слой образуется в результате специфической адсорбции на поверхности электрода ионов одного знака (рис.2.3).

адсорбционный двойной электрический слой
адсорбционный двойной электрический слой
Специфическая адсорбция может происходить и на заряженной (рис.2.3) и на не заряженной поверхности металла (рис.2.4). К адсорбированным ионам со стороны раствора притягиваются ионы противоположного знака. При этом образуется двойной электрический слой, который называется адсорбционным двойным электрическим слоем.
Если знаки заряда обкладок со стороны металла и со стороны раствора одинаковы, то скачки потенциалов в обменном и 22
адсорбционном двойных электрических слоях складываются и наоборот.
3. Двойной электрический слой образуется за счет адсорбции дипольных молекул.
Если поверхность металла заряжена, то к ней будут притягиваться дипольные молекулы растворителя. Ориентация молекул приводит к образованию двойного электрического слоя.
4. Двойной электрический слой образуется в результате выхода электронного газа на некоторое время за пределы границы металла.
В результате этого на поверхности металла со стороны раствора появляется избыточный отрицательный заряд, а со стороны металла -избыточный положительный заряд. Это и приводит к образованию двойного электрического слоя и соответственно к образованию скачка потенциала, который называется контактным потенциалом.
Как правило, все виды двойных электрических слоев реализуются одновременно. Если сумма скачков потенциалов во всех двойных электрических слоях равна нулю, то на поверхности металла имеется абсолютный нуль потенциала. Потенциал, при котором отсутствует обменный двойной электрический слой, называется потенциалом нулевого заряда.
Двойной электрический слой состоит из плотной и диффузной частей. Плотный двойной электрический слой образован плотно притянутыми к поверхности металла электрическими силами и силами специфической адсорбции ионами. Эти ионы расположены на расстоянии радиуса d сольватированного иона.
Диффузный двойной слой образован ионами, расположенными на расстоянии больше d от поверхности электрода. Такое расположение ионов получается под влиянием двух противоположных факторов:
электростатических сил, которые стремятся притянуть ионы плотно к поверхности электрода, и теплового движения, которое стремится хаотически расположить ионы в растворе.
Плотность заряда в плотном двойном электрическом слое равномерно убывает от поверхности. Плотность заряда в диффузном двойном электрическом слое убывает постепенно до нуля по мере удаления от поверхности электрода. Фактически же на расстоянии в несколько десятков атомных диаметров от поверхности электрода плотность зарядов становится пренебрежительно малой.
Скачок потенциала в диффузном двойном слое называют диффузным ψ-потенциалом. Общий скачок потенциала φ Скачок потенциала в плотном двойном слое φ-ψ,.
С увеличением концентрации раствора электролита двойной электрический слой сжимается, ионы приближаются к поверхности электрода и большая их часть из диффузного двойного электрического слоя переходит в плотный двойной электрический слой.
Кроме диффузного ψ -потенциала еще существует адсорбционный ψ — потенциал. Его возникновение связано со специфической адсорбцией ионов (рис.2.7.а, б) на поверхности электрода. Знак адсорбционного ψ — потенциала может совпадать и не совпадать со знаком общего потенциала электрода φ (рис 2.8.а, б). Для случая (2.7.6) потенциал электрода изменяется как показано на рис(2.8.а), а для случая (2.7.а) — как на рис(2.8.б).

3. Лабораторные работы с применением потенциометрического метода.
Метод потенциометрии основан на определении электродных потенциалов измерением ЭДС различных электрохимических цепей.
1. Образование двойного электрического слоя на границе металл-раствор; возникновение скачка потенциала;
2. Электродный потенциал, нормальный потенциал. Ряд напряжения.
3. Типы и виды электродов; зависимость потенциалов электродов, от концентрации образующихся ионов;
4. Гальванические элементы. ЭДС гальванических элементов;
5. Химические и концентрационные гальванические элементы. Выражение для ЭДС гальванических элементов;
6. Термодинамика гальванических элементов;
7. Применение метода ЭДС для определения коэффициента активности раствора, констант равновесия, рН растворов.
1., . Физическая химия. М.: Высшая школа. 1899. Гл. VII. С.248-282.
Работа 1. Измерение ЭДС элемента Якоби-Даниэля.
Целью работы является освоение методики измерения ЭДС гальванического элемента.
Гальванический элемент Якоби-Даниэля состоит из медного и цинкового электродов. Гальваническая цепь элемента записывается следующим образом:
(+)Си|Си, CuSO

При работе гальванического элемента его разность потенциалов не остается постоянной вследствие изменений, происходящих на электродах. Поэтому для измерения ЭДС применяется метод компенсации, который основан на измерении ЭДС элемента по разности потенциалов в условиях обратимости. Для измерения ЭДС можно использовать высокоомный потенциометр постоянного тока Р306 или рН-метр. Необходимо сначала изучить схему измерительной установки и последовательность проводимых измерений на приборе. После этого собирают гальванический элемент.
Выполнение работы. Медную и цинковую пластинки перед погружением в раствор зачищают наждачной бумагой, промывают водой, обезжиривают с помощью ацетона или спирта и вновь тщательно промывают.
В разные сосуды(стаканчики на 100 мл) наливают растворы СиSO и ZnSO
ЭДС гальванического элемента измеряют при различных концентрациях растворов. Перед каждым измерением необходимо выдерживать электроды в растворах 10-15 мин. Полученные данные записываются в табл. 1.
Экспериментально измеренные величины ЭДС необходимо сопоставить с теоретически рассчитанными по уравнению (1.26). Необходимые для теоретического расчета величин ЭДС значения стандартных электродных потенциалов медного и цинкового электродов и средние коэффициенты активности растворов электролитов взять в справочнике.
Таблица 1. Результаты измерения ЭДС элемента Якоби-Даниэля
🔍 Видео
ФИЗИКА ЗА 5 МИНУТ - ТЕРМОДИНАМИКАСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Законы Термодинамики. Что Такое Термодинамика?Скачать

ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать

Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

ВСЯ МКТ И ТЕРМОДИНАМИКА ЗА 6 ЧАСОВ С НУЛЯ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов I Global_EEСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Урок 171. Простейшие задачи на 1-й закон термодинамикиСкачать

Термодинамические параметры. Основное уравнение МКТСкачать

Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Урок 173. Задачи на 1-й закон термодинамики - 1Скачать

Термодинамика | равновесные процессыСкачать