Электрическая потенциальная энергия для двух точечных зарядов зависит от уравнения (4 видео)

Содержание

Оборудование
Наши партнеры
Наши услуги
Полезная информация
Принцип суперпозиции. Потенциальная энергия взаимодействия зарядов.
Принцип суперпозиции.
Потенциальная энергия взаимодействия зарядов.
Потенциальная энергия двух зарядов
Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля
Энергия системы неподвижных точечных зарядов
Энергия заряженного уединенного проводника
Энергия заряженного конденсатора
Энергия электростатического поля
📺 Видео

Оборудование

Наши
партнеры

Наши
услуги

Полезная
информация

Видео:Лекция 5-3 Энергия взаимодействия точечных зарядовСкачать

Принцип суперпозиции. Потенциальная энергия взаимодействия зарядов.

Видео:Электрическая потенциальная энергияСкачать

Принцип суперпозиции.

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q больше 0, то вектор напряженности направлен от заряда, если Q меньше 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

1. Нарисовать рисунок.

2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.

3. Вычислить каждую из напряжённостей по соответствующей формуле.

4. Сложить вектора напряжённостей геометрически (т.е. векторно).

Видео:Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Потенциальная энергия взаимодействия зарядов.

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывает потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

Видео:ph0411 Потенциальная энергия взаимодействия точечных зарядовСкачать

Потенциальная энергия двух зарядов

Рассчитаем потенциальную энергию W_эл(r) двух одноименных зарядов q и Q, находящихся на расстоянии r друг от друга (рис 2.3). Заряды отталкиваются с силой

. (2.9)

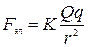
Рис 2.3. Силы, действующие между одноименными зарядами

Коэффициент пропорциональности К зависит от выбора единиц измерения зарядов. В СИ заряды измеряются в кулонах (Кл) и К = 9·10 9 Н·м/Кл 2 .

Чтобы перевести заряд q из «нулевой конфигурации», т.е. из бесконечности в точку r, надо совершить работу

(2.10)

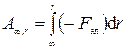
по преодолению электрической силы отталкивающихся зарядов. Знак минус связан с тем, что (F_эл^dr)=cosπ=-1, т. к. сила и перемещение противоположно направлены. Подставляя (2.9) в (2 10), имеем

. (2.11)

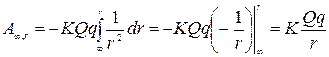
Следовательно, потенциальная энергия двух одноименных точечных зарядов пропорциональна произведению зарядов и обратно пропорциональна расстоянию между ними:

. (2.12)

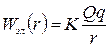
Рис 2 4 Зависимость потенциальной энергии двух одноименных зарядов

от расстояния между ними

На рис 2 4 приведена потенциальная энергия двух положительных зарядов в зависимости от расстояния r между ними. Поскольку система всегда стремится к минимуму своей энергии, то ясно, что одноименные заряды стремятся разойтись друг от друга на большое расстояние.

Для двух разноименных зарядов потенциальная энергия равна

. (2.13)

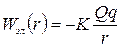
Положительная потенциальная энергия означает, что для сближения зарядов требуется затратить работу. Отрицательная потенциальная энергия означает, что работа будет затрачиваться при удалении зарядов друг от друга.

З а д а н и е: нарисуйте зависимость потенциальной энергии двух зарядов от расстояния.

Видео:Потенциальная энергия заряженного тела в электростатическом поле | Физика 10 класс #49 | ИнфоурокСкачать

Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля

Электростатические силы взаимодействия консервативны; следовательно, система зарядов обладает потенциальной энергией.

Видео:Потенциальная энергия взаимодействия зарядовСкачать

Энергия системы неподвижных точечных зарядов

Найдем потенциальную энергию системы двух точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией:

где φ₁₂ и φ₂₁ — соответственно потенциалы, создаваемые зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Потенциал поля точечного заряда равен:

Добавляя к системе из двух зарядов последовательно заряды Q₃, Q₄, …, можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

где _i — потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Видео:Урок 232. Электрон-вольт. Потенциал поля точечного зарядаСкачать

Энергия заряженного уединенного проводника

Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны Q, С, φ. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, затратив на это работу, равную

Чтобы зарядить тело от нулевого потенциала до , необходимо совершить работу

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

Эту формулу можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Полагая потенциал проводника равным , из (3) найдем

где – заряд проводника.

Видео:Закон КулонаСкачать

Энергия заряженного конденсатора

Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой (4) равна

где Q — заряд конденсатора, С — его емкость,  — разность потенциалов между обкладками.

Используя выражение (5), можно найти механическую силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину dx. Тогда действующая сила совершает работу

вследствие уменьшения потенциальной энергии системы

Подставив в (5) в формулу емкости плоского конденсатора, получим

Производя дифференцирование при конкретном значении энергии (см. (6) и (7)), найдем искомую силу:

где знак минус указывает, что сила F является силой притяжения.

Видео:Урок 213. Электрические заряды и их взаимодействие. Закон КулонаСкачать

Энергия электростатического поля

Преобразуем формулу (5), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воcпользовавшись выражением для емкости плоского конденсатора (C = ₀S/d) и разности потенциалов между его обкладками ( = Ed). Тогда получим

где V = Sd — объем конденсатора. Эта формула показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле,— напряженность Е.

Объемная плотность энергии электростатического поля (энергия единицы объема)

Формулы (5) и (8) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализации электростатической энергии и что является ее носителем — заряды или иоле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т. е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные вопросы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о локализации энергии в поле и что носителем энергии является поле.