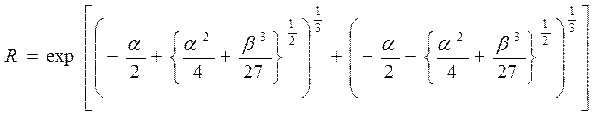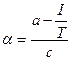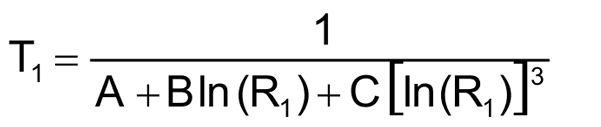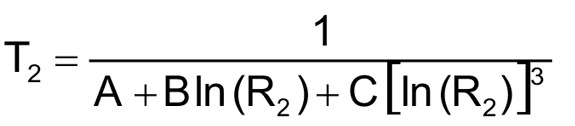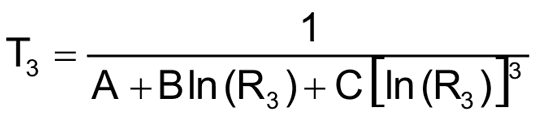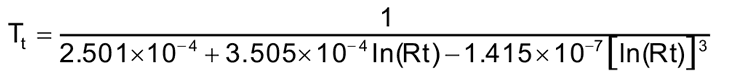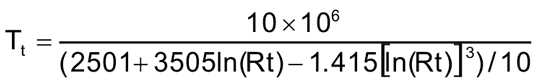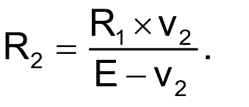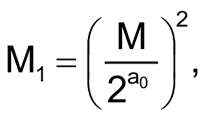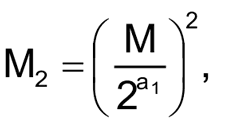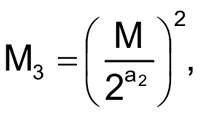Использование терморезистора (термистора) – один из самых простых и дешевых способов измерения температуры. Для точного измерения температуры с помощью терморезистора необходим микроконтроллер, в качестве которого в нашем проекте мы будем использовать плату Arduino. Измеренное значение температуры будет отображаться на экране ЖК дисплея. Подобная схема может найти применение в удаленных метеорологических станциях, проектах автоматизации (умного) дома, управления электронным и промышленным оборудованием.
Видео:Определение коэффициента вязкости жидкости методом СтоксаСкачать
Необходимые компоненты
- Плата Arduino (любая модель) (купить на AliExpress).
- ЖК дисплей 16х2 (купить на AliExpress).
- NTC thermistor 10 кОм (терморезистор с отрицательным температурным коэффициентом) (купить на AliExpress).
- Резистор 10 кОм (купить на AliExpress).
- Соединительные провода.
Видео:Урок 104 (осн). Экспериментальное определение коэффициента объемного расширения жидкостиСкачать
Работа схемы
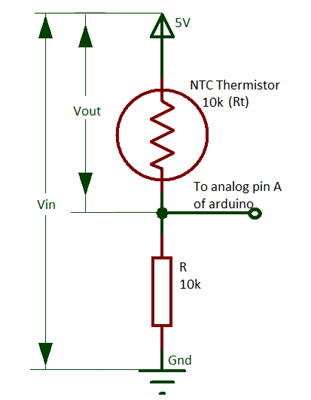
Схема устройства представлена на следующем рисунке.
При изменении температуры изменяется сопротивление терморезистора (термистора). Но в нашей схеме мы не будем измерять сопротивление термистора напрямую, вместо этого мы использовали делитель напряжения, одним из резисторов которого является известное сопротивление 10 кОм, а вторым – наш терморезистор. Средняя точка делителя напряжения подключена к аналоговому входу A0 платы Arduino, поэтому при помощи аналогово-цифрового преобразования (АЦП) на этом контакте мы можем определить падение напряжение на терморезисторе в любой момент времени и, следовательно, и его сопротивление. Благодаря этим данным мы по формулам, приведенным ниже в данной статье, можем определить значение температуры.
Видео:Решение задач на термохимические уравнения. 8 класс.Скачать
Терморезистор
Ключевым компонентом нашей схемы является терморезистор, который используется для определения температуры. Термистор представляет собой резистор, сопротивление которого изменяется в зависимости от температуры. Существует два типа подобных термисторов: NTC (Negative Temperature Co-efficient — с отрицательным температурным коэффициентом) и PTC (Positive Temperature Co-efficient — с положительным температурным коэффициентом). Мы в нашем проекте будем использовать терморезистор NTC типа – его сопротивление уменьшается с повышением температуры. На следующих рисунках приведены график зависимости сопротивления подобного терморезистора от температуры и его типовой внешний вид.
 |  |
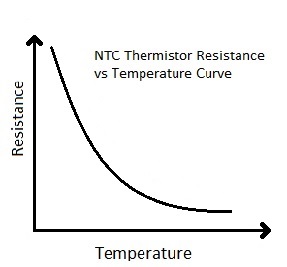Расчет температуры с помощью терморезистора
Схема используемого нами делителя напряжения представлена на следующем рисунке.
Напряжение на терморезисторе в этой схеме можно определить из известного напряжения:
Из этой формулы можно выразить значение сопротивления терморезистора Rt (R – известное сопротивление 10 кОм):
Значение Vout мы затем будем определять в коде программы с помощью считывания значения на выходе АЦП на контакте A0 платы Arduino.
Математически, сопротивление терморезистора можно вычислить с помощью известного уравнения Стейнхарта-Харта (Stein-Hart equation).
T = 1/(A + B*ln(Rt) + C*ln(Rt) 3 ) .
В этой формуле A, B и C — константы, Rt – сопротивление терморезистора, ln — натуральный логарифм.
Мы для проекта использовали терморезистор со следующими константами: A = 1.009249522×10 −3 , B = 2.378405444×10 −4 , C = 2.019202697×10 −7 . Эти константы можно определить с помощью данного калькулятора, введя в нем значения сопротивления терморезистора при трех значениях температуры или вы их можете непосредственно узнать из даташита на ваш терморезистор.
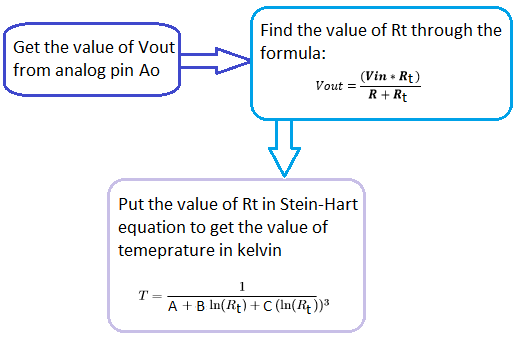
Таким образом, для определения значения температуры нам будет нужно только значение сопротивления терморезистора – после его определения мы просто подставляем его значение в уравнение Стейнхарта-Харта и с его помощью рассчитываем значением температуры в кельвинах. Алгоритм определения температуры в нашем проекте представлен на следующем рисунке.
Видео:Урок 228 (осн). ЛР Определение коэффициента ослабления гамма-излучения различными материаламиСкачать
Исходный код программы
Полный код программы представлен в конце статьи, здесь же сначала рассмотрим его наиболее важные фрагменты.
Для выполнения математических операций в программе мы должны подключить заголовочный файл библиотеки “ #include >”, а для работы с ЖК дисплеем – подключить библиотеку “ #include
«. Далее в функции setup() мы должны инициализировать ЖК дисплей.
Видео:Лабораторная работа «Измерение коэффициента трения скольжения»Скачать
Уравнения для термисторов
Точного уравнения для описания поведения термистора не существует, – имеются только приближенные. Рассмотрим два широко используемых приближенных уравнения.
Первое приближенное уравнение, экспоненциальное, вполне удовлетворительно для ограниченных температурных диапазонов, в особенности – при использовании термисторов с малой точностью. Второе уравнение, называемое уравнением Стейнхарта-Харта, обеспечивает прекрасную точность для диапазонов до 100 о С.
Сопротивление термистора с отрицательным ТКС уменьшается приблизительно по экспоненте с увеличением температуры. В ограниченных температурных диапазонах его R-T-зависимость достаточно хорошо описывается следующим уравнением:
Где Т1 и Т2 – абсолютные температуры в градусах Кельвина ( о С +273) ;
RT1 и RT2 – сопротивления термистора при Т1 и Т2; b — константа, определяемая путем измерения сопротивления термистора при двух известных температурах.
 |
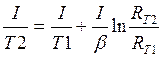Если b и RT1 известны, то это уравнение можно преобразовать и использовать для вычисления температуры, измеряя сопротивление:
Бета является большим, положительным числом и имеет размерность в градусах Кельвина. Типовые значения изменяются от 3000 до 5000 о К.
Изготовители часто включают значения для бета в спецификации, однако, так как экспоненциальное уравнение является лишь приблизительным, значение бета зависит от двух температур, использованных при его вычислении. Некоторые изготовители используют значения 0 и 50 о С; другие – 25 и 75 о С.
Можно использовать другие температуры: можно вычислить самостоятельно значение бета на основании таблиц зависимости сопротивления от температуры, которые предлагает изготовитель. Уравнение, как правило согласуется с измеренными значениями в пределах ± 1 о С на участке в 100 о С. Уравнение нельзя использовать с достоверностью при температурах, сильно отличающихся от тех, что были использованы для определения бета.
Перед тем, как перейти к уравнению Стейнхарта-Харта, рассмотрим два других параметра, часто используемых для описания термисторов: альфа (a) и коэффициент сопротивления. Альфа просто определяется наклоном R-T- кривой, то есть является чувствительностью при определенной температуре. Альфа обычно выражается в «процентах на градус». Типовые значения изменяются от 3 % до 5 % о С. Так же, как и бета, альфа зависит от температур, при которых она определяется. Её значение несколько уменьшатся при более высоких температурах.
Под коэффициентом сопротивления подразумевается отношение сопротивления при одной температуре к сопротивлению при другой, более высокой температуре.
Для точных термисторов обычно имеется таблица значений сопротивления (с шагом 1 °С) в зависимости от температуры, которая поставляется изготовителем вместе с другой информацией. Однако иногда удобно иметь точное уравнение при выполнении конструкторских расчетов или (особенно) при использовании ЭВМ для пересчета сопротивления термистора в температуру. Кроме как для очень узких диапазонов температур, экспоненциальное уравнение с одним параметром не удовлетворительно – необходимо большее число параметров.
Наилучшим приближенным выражением, широко используемым в настоящее время, является уравнение Стейнхарта-Харта:
 |
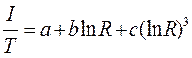Где Т- абсолютная температура (в градусах Кельвина), R – сопротивление термистора; а, b и с –экспериментально полученные константы.
Преобразование уравнения с целью выражения сопротивления в виде функции температуры приводит к довольно громоздкому на вид выражению. Однако, с ним легко обращаться при использовании ЭВМ или программируемого калькулятора:
Где и .
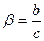
Необходимо отметить, что данные значения для альфа и бета не относятся к параметрам альфа и бета, используемым в экспоненнциальном уравнении с одним параметром.
Хотя уравнение Стейнхарта-Харта – более сложное, оно, как правило, согласуется с реальными значениями в пределах нескольких тысячных градуса в диапазонах до 1000 о С. Конечно, оно может быть настолько хорошим, если только экспериментальные значения параметров термистора также точны. Температуры с точностью до тысячных градуса можно получить только в первоклассных лабораториях. Скорее пользователь согласится пользоваться паспортными таблицами, чем захочет провести собственные измерения.
Для определения a, b и с необходимо знать точное сопротивление термистора при трёх температурах и подставить каждый набор данных (R и Т) в уравнение Стейнхарта-Харта для определения трех неизвестных. Затем необходимо использовать математические средства для одновременного решения трёх уравнений и получения значений трёх констант. При использовании паспортных таблиц нужно выбирать значения R в зависимости от Т на краях и в середине температурного диапазона, который будет использоваться. Изготовители обычно не указывают паспортные значения для этих констант, так как эти значения изменяются в зависимости от используемого температурного диапазона.
Видео:ЛР-10-2-03 Определение коэффициента поверхностного натяжения методом отрыва капельСкачать
Микроконтроллер решает сложные полиномиальные уравнения
Видео:Как расставить коэффициенты в органических ОВР? | Екатерина СтрогановаСкачать
LM103 PIC16F887
Ricardo Jimenez и Roberto Solorio
С помощью выполняющейся за короткое время программы и простой схемы микроконтроллер PIC может линеаризовать характеристику термистора, чтобы точно измерить температуру и отобразить результат на дисплее.
Измеряя температуру с помощью термистора, вы сталкиваетесь с проблемой линеаризации его отклика, необходимой для получения результатов требуемой точности. Одним из лучших методов линеаризации термистора является использование полиномиального уравнения Стейнхарта-Харта, дающего ошибку в 0.1 °C. Описываемая ниже конструкция рассчитана на диапазон температур от 0 °C до 100 °C.
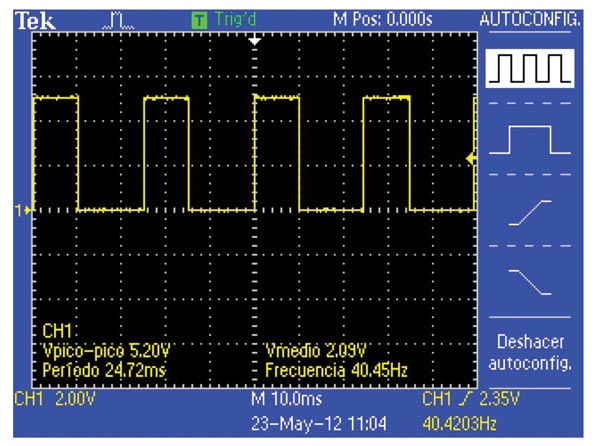
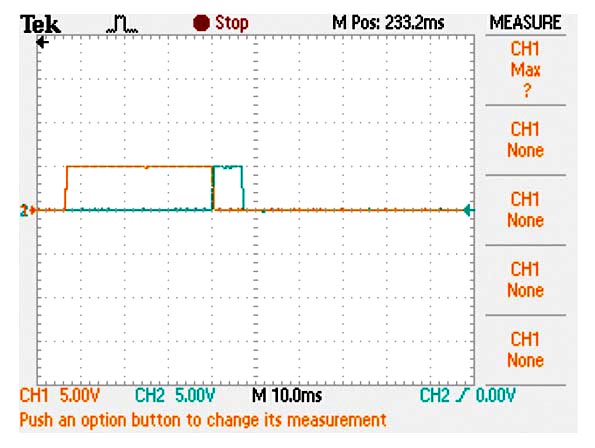
Для того чтобы составить уравнение, потребуются три коэффициента термистора – A, B и C. Если изготовитель не предоставил такую информацию, вы можете найти коэффициенты, решив уравнения Стейнхарта-Харта (1…3) для трех различных температурных точек. В нашей схеме микроконтроллер PIC с необходимой точностью решает эти уравнения за 40 мс (Рисунок 1).
 | |
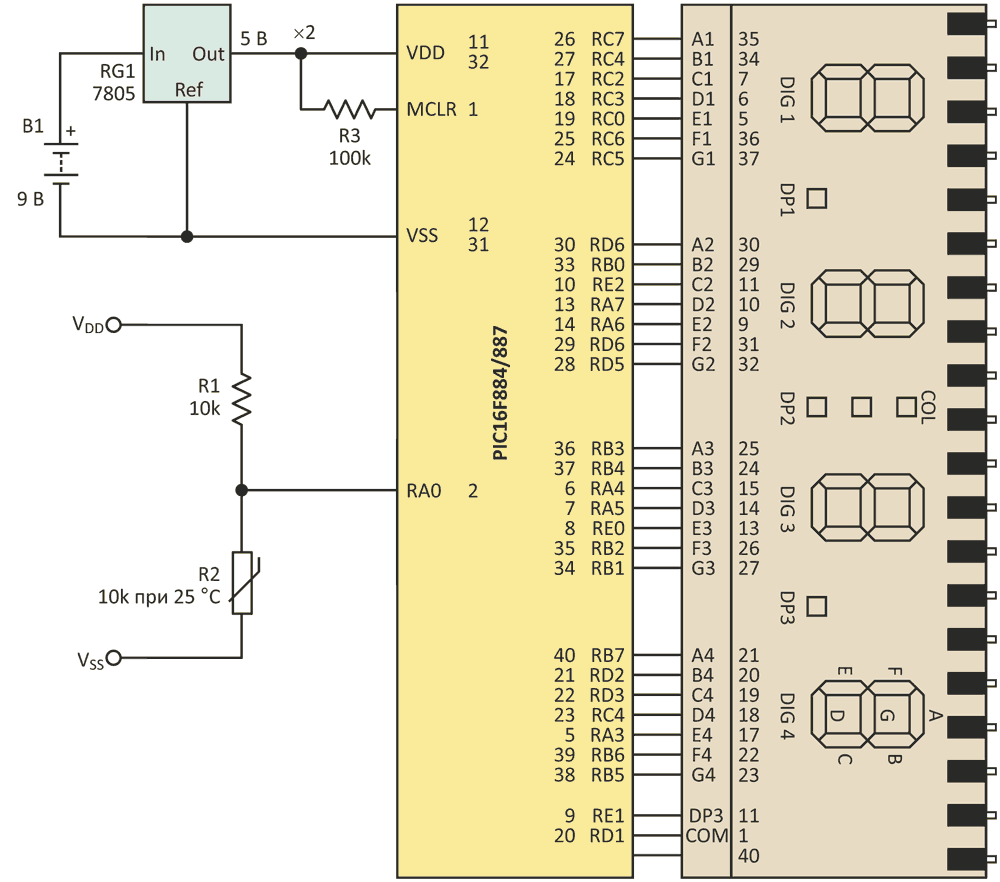| Рисунок 1. | В этой простой схеме высокоточного термометра используется микроконтроллер PIC16F887 и ЖК индикатор. |
Для иллюстрации воспользуемся термистором LM103 с отрицательным температурным коэффициентом (NTC), сопротивление которого при трех различных температурах имеет значения, показанные в Таблице 1.
| Таблица 1. | Сопротивление термистора. | ||||||||||||||||||||||||||||||
Решая эту систему из трех уравнений, получаем коэффициенты A, B и C (Таблица 2).
| |||||||||||||||||||||||||||||||
