| Спин электрона. Опыт Штерна и Герлаха |   |
В 1922 году немецкие физики О. Штерн и В. Герлах поставили опыты, целью которых было измерение магнитных моментов Pm атомов различных химических элементов. Для химических элементов, образующих первую группу таблицы Менделеева и имеющих один валентный электрон, магнитный момент атома равен магнитному моменту валентного электрона, т.е. одного электрона. Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности. Схема опыта изображена на рис. 7.9. В колбе с вакуумом, 10 –5 мм рт. ст., нагревался серебряный шарик К, до температуры испарения. Атомы серебра летели с тепловой скоростью около 100 м/с через щелевые диафрагмы В и, проходя резко неоднородное магнитное поле, попадали на фотопластинку А. Если бы момент импульса атома Этим доказывался квантовый характер магнитных моментов электронов. Количественный анализ показал, что проекция магнитного момента электрона равна магнетону Бора: Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора. Опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора (ħ – единица измерения механического момента импульса). Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s—состояние). Но при l = 0 В 1925 г. студенты Геттингенского университета Гаудсмит и Уленбек предположили существование собственного механического момента импульса у электрона Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха. Авторы дали такое толкование спина: электрон – вращающийся волчок. Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью, равной 300 с, где с – скорость света. От такого толкования спина пришлось отказаться. В современном представлении – спин, как заряд и масса, есть свойство электрона. П. Дирак впоследствии показал, что существование спина вытекает из решения релятивистского волнового уравнения Шредингера. Из общих выводов квантовой механики следует, что спин должен быть квантован: Аналогично, проекция спина на ось z (Lsz) (ось z совпадает с направлением внешнего магнитного поля) должна быть квантована и вектор Из опытов Штерна и Герлаха следует, что таких ориентаций всего две: Для атомов первой группы, валентный электрон которых находится в s—состоянии (l = 0), момент импульса атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов пространственное квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле. (Опыты с электронами в p—состоянии подтвердили этот вывод, хотя картина получилась более сложной) (желтая линия натрия – дуплет из-за наличия спина). Численное значение спина электрона: По аналогии с пространственным квантованием орбитального момента где Итак, проекция спинового механического момента импульса на направление внешнего магнитного поля может принимать два значения:
Так как мы всегда имеем дело с проекциями, то говоря, что спин имеет две ориентации, имеем в виду две проекции. Проекция спинового магнитного момента электрона на направление внешнего магнитного поля: Отношение Содержание Видео:Как проводится эксперимент Штерна — Герлаха? Душкин объяснитСкачать  Расставляя все точки над «пси»
При планировании нескольких статей так или иначе связанных с квантовой механикой было решено вынести обсуждение ряда технических вопросов, философских споров и досужих мифов в отдельную статью. Речь пойдет о самом сложном и интересном инструменте человеческого интеллекта — квантовой теории.
Большая часть нашей коллективной деятельности регулируется другими людьми. Мы получаем от них набор условных обозначений и правила их использования. Владение таким инструментом позволяет нам принимать сообщения и отвечать так, чтоб максимально точно передать результат работы своей нейронной сети. Человеческие правила коллективной деятельности определяют эволюцию нашей культуры. Напротив, природные системы, от атомов до галактик, развиваются независимо от человеческих правил. Мы не можем изменять физические законы. Мы можем только попытаться понять их. Сама природа судит посредством экспериментов, насколько правдоподобно то или иное объяснение некоторых природных явлений. Тем не менее, в передовых исследованиях, где неизвестное только начинает обретать форму, новое знание достаточно неустойчиво. Для должного обоснования модели исследователь обязан иметь обширный фундамент. По аналогии с высказыванием «ты — то что ты ешь» справедливо то, что мы оперируем при мышлении лишь знаниями поступившими извне (разумеется с учетом предустановок обусловленных на начальных этапах формирования мозга). Тут уже приходится полагаться помимо собственного чувственного опыта на утверждения окружающих. И не абы кого, а авторитетов.
Для того, чтобы быстро восполнить какой-либо пробел, достаточно вбить в поисковик ключевую фразу, а ля «двухщелевой эксперимент» и пробежаться глазами по предложенным источникам. И пожалуйста, у вас есть знание — быстро, дешево, наглядно! Теперь вы знаете ответ на вопрос и можете даже написать свою статью, чтоб учить окружающих. И она будет иметь шанс выпасть в поисковой выдаче. Вот только почему-то многие не обращают внимание на то, кто был автором ответов. Ютюбовское видео — блогер, бросивший учебу, но популярный из-за смазливой мордашки и умения вставлять мультики в ролик; запись из блога — школьница подросток увлекающаяся астральными путешествиями; статья из научпоп журнала — журналистка, чья специальность не подразумевала никаких технических дисциплин. Конечно, из любого правила есть исключения, и приходится просматривать большую часть работ автора, чтоб сделать о нем выводы. Может по образованию она и журналистка, но на досуге листает твёрдую литературу. Однако, по вопросам физических моделей я пойду к знакомому доктору физико-математических наук, за объяснением когнитивных процессов полезу в книги специалиста по нейроанатомии, а рецепт наивкуснейших печений спрошу у сестры. Нам приходится полагаться на мнения специалистов для экономии времени и сил. Если проверять все утверждения и успешные теории самому, то человеческой жизни не хватит, чтоб догнать современный уровень развития общества. От того вера учителям становится необходимой. При этом нужно всегда держать в уме, что они такие же люди и не застрахованы от ошибок, пороков и профдеформации. И будучи мастером своего дела человек будет полнейшим профаном в других аспектах. Даже в пределах одной области познания, мнения у именитых специалистов могут отличаться весьма и весьма. Скажем, Р. Пенроуз будет больше внимание уделять математике, везде и всюду вспоминать Гёделя, а сложную проблему разума спихивать на квантовые явления. Л. Сет — приверженец инженерного подхода, основной упор делает на теорию информации и детерминизм. С. Ааронсон как истинный программист больше внимания уделяет соотношению сложностей вычислений и квантовой информатике. Физики экспериментаторы предрасположены к позитивизму и материализму. Математики (чаще подверженные комплексу величия) склонны к идеализму, антропоцентризму, а то и солипсизму. Биологи и медики менее религиозны и антропоцентричны чем первые и вторые. А химики… Хм, нужно побольше разузнать про мировосприятие химиков.
В общем, чтобы осмыслять окружающий мир приходится верить тем, кто убивал время на его понимание. А чтобы понять самому, придется поработать ручками и головой. Видео:Опыт Штерна и Герлаха, Леннаучфильм, 1977Скачать  Где взять понимание
В нашу эпоху доступной информации важно умение отделять зерно от плевел. Чтобы оперировать определенными образами, нужно рассмотреть проблему с разных ракурсов ознакомившись с точками зрения нескольких авторов. Еще нужно много практики. Квантовая теория это в первую очередь инструмент, а не философское течение, где каждый волен озвучить свое мнение. Для использования этого сложного инструмента нужны инструкции и учителя.
Гуго Штейнгауз как-то сказал: «математик сделает это лучше». Под «это» подразумевается всё. Оно и понятно, ведь занятие точными науками есть многогранная тренировка мышления и привнесение в ум дисциплинированности. Так что, без должных навыков из линейной алгебры, дифференциального исчисления и математической логики с теорией алгоритмов путь в теоретическую физику закрыт. Все остальное самообман и иллюзия понимания — вы просто не будете восприимчивым к грамотным объяснениям, так как мышление не будет генерировать образов, которые пытается донести собеседник или автор касательно данной темы. Только разобравшись со вспомогательными инструментами из матана и с основами классической физики (механика, электродинамика, оптика, статы) можно приступать к квантам. Тут не сдержусь порекомендовать литературу «которая навсегда перевернет ваше сознание»
Если вы не проявляли усилий для основательного освоения материала, то будьте честны хотя бы с собой — вы сторонний наблюдатель и нефига в квантах не смыслите. Не встревайте в споры, не выдвигайте теории и уж тем более не учите окружающих. Ну да, это наболевшее. Ладно здесь на хабре и еще много на каких технических форумах и тематических группах проскакивает дичь, порожденная необразованностью автора, но когда два профессора подряд на лекциях по философии упраздняли квантовую механику и теорию относительности, тут уж мне многое пришлось переосмыслить. Однако же, на время отвлечемся от пространных разговоров и поработаем руками. Видео:Квантовая механика 2 - Эксперимент Штерна-Герлаха. Спин электрона.Скачать  Уравнение Шредингера
В наиболее общем случае эволюцию (переход между состояниями) абстрактной системы можно описать взаимно-однозначными афинными преобразованиями фазового пространства: Введя унитарный оператор U, мы имеем Для непрерывной однопараметрической группы унитарных операторов удовлетворяющей условиям:
работает теорема Стоуна
где H — эрмитов оператор, а параметр t обычно играет роль времени. И вот, для векторов чистых состояний
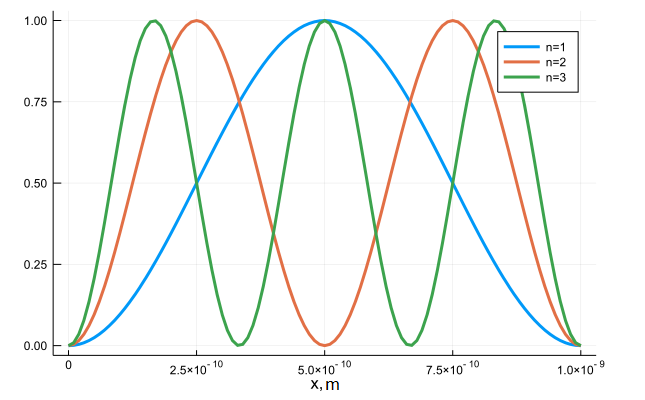
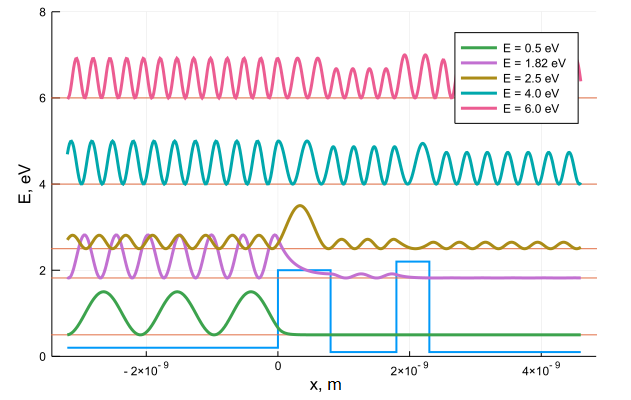
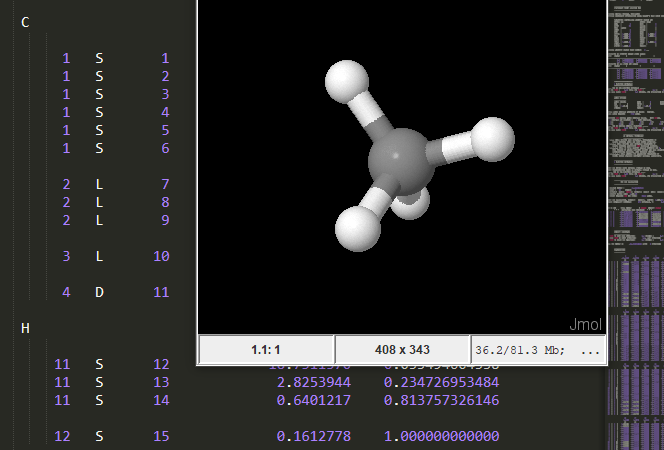
Из терминологии классической механики: Тем кто полюбил линейную алгебру занимаясь компьютерной графикой (привет пользователям OpenGL), уравнение как бы намекает, что эволюция чистой квантовой системы это повороты вектора состояния путем умножения на матрицу-гамильтониан. Формально, уравнение Шредингера ни откуда не выводится, будучи в нерелятивистской квантовой механике наиболее общим. Оно постулируется как обобщение экспериментов. Хотя, в книге Бома можно посмотреть довольно органичный способ его получения на основе выражения волны для свободной частицы. Практически вся волновая теория заключена в волновом уравнении, если мы знаем, как интерпретировать волновую функцию. Уравнение Шредингера является математическим выражением корпускулярно-волнового дуализма микрочастиц. В предельном случае, когда длины волн де Бройля значительно меньше размеров рассматриваемого движения, уравнение Шредингера позволяет описывать движение частиц по законам классической механики.
С математической точки зрения — это дифференциальное уравнение в частных производных, которое имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи. С физической точки зрения нужно отметить, что согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в которой движение системы заранее предопределено начальными условиями. Однако сама волновая функция имеет вероятностный смысл. Наконец, необходимо отметить важную особенность уравнения Шредингера: оно линейно. Волновая функция и ее производные входят в него в первой степени и для волновых функций справедлив принцип суперпозиции. Он позволяет сложные модели разбивать на подзадачи. Факторизуя волновую функцию на временную и на пространственные компоненты получаем одномерное стационарное Уравнение Шредингера
Это ни что иное, как задача на собственные значения оператора Гамильтона. Энергия – одна из наблюдаемых, следовательно, это уравнение на допустимые наблюдаемые значения энергии и на соответствующие им состояния системы. Получим общее решение для нулевого потенциала:
Теперь знай себе, подставляй граничные и начальные условия в зависимости от задачи. Так можно получить, например, аналитическое выражение для свободной частицы в потенциальной яме, дающее вероятности локализации в некотором пространстве
К этой модели сводится, например, движение Если же учитывать внешний потенциал (а он разнится в зависимости от среды) то волновую функцию в некой слоистой структуре можно представить в виде:
Используя граничные условия и довольно красивый метод матриц переноса получаем спектр и собственные функции для последовательности произвольных постоянных потенциалов
Этой же методой выуживают значения энергии резонансных переходов электронов в слоисто-неоднородных средах. Чтобы не перегружать страницу формулами и кодом укажем ссылки на исходники и pdf-аналоги: раз два Видео:Опыт ШтернаСкачать  Численные методыОчень хорошо когда задача сводится к известной модели. Но не всегда удается получить аналитическое решение. Поэтому в квантмехе найдется работа не только чистым теоретикам, но и грязным числодробителям. Уравнение Шредингера вполне себе типичная дифура, для которых разработана уйма методов. Поиграем с одним из них. Разностная аппроксимация по времени уравнения Шредингера с использованием метода Кранка-Николсона имеет вид:
Которую можно переписать в виде:
В одномерном случае конечно-разностная схема по координате расписывается как:
Это соответствует построению для гамильтониана разреженной матрицы. Например, для
Вот и все, теперь достаточно задать начальный волновой пакет, вид потенциального барьера, взять побольше шагов по времени и координате и пожалуйста — анимации квантовых явлений рассчитанные силами вашего пк:
Еще может быть интересна имплементация расщепления шага Фурье и решение несколькими методами нелинейного уравнения Шредингера находящего применение в физике плазмы, в частности при моделировании нелинейных быстрых магнитозвуковых волн в корональных магнитных трубках. Но разумеется не все так радужно. Чем больше объектов в изучаемой системе, тем сложнее будет модель. Например, для молекулы воды в оператор Гамильтона будут входить импульсы трех ядер (два ядра водорода и одно кислорода) и 10 электронов, а также потенциалы кулоновского взаимодействия всех пар частиц:
И какой же ужас нас ждет когда мы захотим промоделировать элементарную химическую реакцию веществ в этой воде растворенных — каждый электронный переход происходит с оглядкой на наведенное поле, в свою очередь влияя на окружающие дипольные моменты молекул воды. А если же вам вздумается моделировать геометрию органических молекул. И тут на помощь приходят семиэмпирические и квазиклассические методы, а также уйма эвристик, упрощений и хитрых солверов.
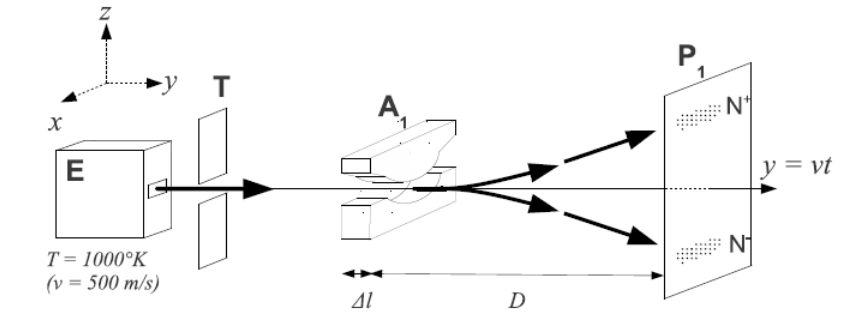
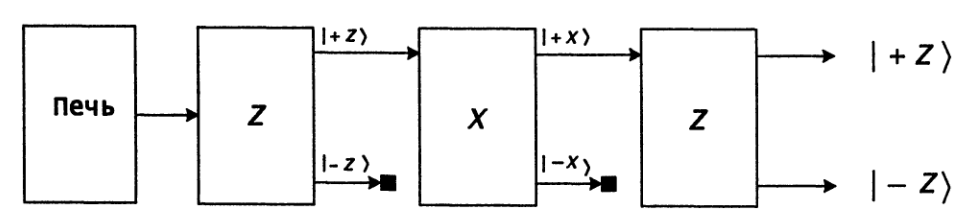
Такого жанра расчеты часто проводятся при проектировании микроэлектроники, в материаловедении, дефектоскопии, медицине и общей химии, то есть в плане практики детище умов двадцатого века находит все больше применений. Если кто-то проталкивает мысль, что волновая механика бесполезна или ничего не объясняет, то значит для него это слишком сложно. Все еще надеюсь, что экзамен по философии пройдет в устной форме, уж тогда-то можно будет отыграться за всю ту боль, что эти гуманитарии причиняли на лекциях 🙂 Однако, перейдем к самым спорным мысленным и реальным экспериментам. Видео:🧪🧪🧪🧪 Доказательство реальности квантового мира. (Часть 1. Квантуемость, спин, прибор Штерна-Герлаха)Скачать  Эксперимент Штерна—ГерлахаХотя наибольшую популярность у общественности снискал опыт Юнга с двухщелевым интерферометром, зарекомендовавшийся как самый контринтуитивный подарок микромира, лично мне больше нравится в этом плане эксперимент Штерна—Герлаха 1922 года
Из печи выпускаются быстрые атомы серебра, которые проходя через сильное магнитное поле образуют на экране зеркальное напыление. Атомы металлов имеют сложную структуру, поэтому для пущей наглядности можно брать водород. Из-за движения электрона в окрестности атома должен возникать магнитный момент, и напрашивается предположение, что в магнитном поле атом ведет себя как маленький магнитик. Имея произвольную начальную ориентацию наши магнитики, испытывая отклонение при прохождении внешнего поля, должны распределиться на экране более-менее равномерно. Не тут-то было! На экране будут кучки, которые можно посчитать по пальцам, а значит магнитные свойства квантуются. Пришлось вводить спин — собственный момент — дающий, наряду с орбитальным, вклад в полный момент атома. И вот измеряя, скажем, Z компоненту мы получаем на выходе из установки два пучка. Видимо электроны делятся на два сорта: на мальчиков и девочек. Теперь затащим в лабораторию рояль и минибар еще одну установку и опрокинем ее набок супротив первой, так чтобы на вход второй подавался один из потоков струящихся из первой.
И на выходе получаем опять два пучка. То есть в новом ортогональном направлении тоже есть свой вклад. Ну ладно, девочки бывают разные… Занесем пилоны и лаборанток еще установку и сориентируем вертикально пристроив к первым двум
И опять на выходе два пучка! Это пошатывает убежденность, что спин является объективной характеристикой, которая может существовать до взаимодействия с экспериментальной установкой. Надеюсь, вы достаточно заинтригованы. Подробные детали и обсуждение результатов каскадного эксперимента Штерна-Герлаха в рамках кубитной модели читайте в книге Квантовые вычисления и квантовая информация М. Нильсен, И. Чанг. Возможно, мы потом вернемся к этому опыту в рамках различных интерпретаций. (todo: поискать эксперименты с различным временем пребывания в МП) Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать  Тот самый кот
Часто кота Шрёдингера используют для нагнетания мистицизма. Этот мысленный эксперимент раздувают до парадокса, им пытаются объяснять сложность и противоречивость квантовой механики или даже утверждают, что ее суть передается этим мемом. В зависимости от уровня абстрактного и критического мышления люди застревают на разных этапах: кто-то начинает спор на счет пола животного, кто-то плачет, что кису жалко, некоторые начинают прикапываться к деталям установки, многие спорят о роли наблюдателя.
С наблюдением вообще отдельная история. В экспериментах под процессом наблюдения понимается взаимодействие исследуемой системы с измерительным прибором. Наблюдателем можно считать и газоразрядный счетчик Гейгера и фотодетектор с мультиметром, а не только человека слушающего треск и видящего показания на дисплее. Для квантовых систем важна их чистота достигаемая изоляцией от внешних воздействий. Именно тогда на достаточно больших временах эволюцию можно описывать уравнением Шрёдингера. Если вы, скажем, поставили детектор возле одной из щелей в опыте Юнга, то получается вы привнесли в систему наблюдателя — многочастичную хреновину ограничивающую пространственные степени свободы исследуемых объектов. Подробней этот вопрос раскрыт в книге Бома в 6 части. Там он очень даже неплохо для 50х годов прошлого века проследил процесс измерения вплоть до мозга экспериментатора. Опять же, нюансы это вопрос интерпретации, но с точки зрения матаппарата всё довольно согласовано и пригодно для практических применений. К слову, если уж совсем не хочется работать с литературой и привычней разжеванный видеоконцентрат, то можно посмотреть хотя бы на материалы по теме от ребят из физтеха. При просмотре вспомнил про подобное объяснение для трехщелевого эксперимента (да, это тот, где выходят отрицательные вероятности) в лекциях по матрицам плотности от Никитина Н.В.
Вернемся к котикам. Объяснения этого эксперимента желательно смотреть не по бложикам и видосикам, а в крепкой литературе. Возможно вы заметите, что во многих монографиях мысленные эксперименты и философия поднимаются в конце, уже после изложения необходимого формализма. Тогда уже приходит понимание, что и кот и ЭПР возникли во времена, когда терминология только формировалась и многим хотелось таким образом выразить свое недовольство какими-либо нюансами. В частности Шредингер с котом хотели заострить внимание на грани между микро- и макро-. Источником проблемы является неопределенность, связанная со статистической интерпретацией волновой функции, которая однозначно не определяет результат измерения. Все, что она дает, — это статистическое распределение возможных результатов. В связи с этим возникает глубокий вопрос: действительно ли физическая система «имела» рассматриваемый атрибут до измерения (так называемая реалистическая точка зрения), или же сам акт измерения «создал» это свойство, ограниченное лишь амплитудой вероятности (ортодоксальная позиция). Или же мы можем списав на метафизику сказать, что никакого смысла в этих спорах нет (агностика ответ). Согласно реализму, квантовая механика — это неполная теория, ибо даже если вы знаете все, что квантовая механика может рассказать вам о системе, вы все равно не можете определить все ее особенности. Очевидно, существует и другая информация, внешняя по отношению к квантовой механике, которая необходима для полного описания физической реальности. Тут уже появляются теории со скрытыми переменными, парочку из которых вместе с неравенствами Белла рассмотрим позже. Ортодоксальная позиция поднимает еще более тревожные проблемы, ибо если акт измерения заставляет систему «занять позицию», помогая создать атрибут, которого раньше не было, то в процессе измерения есть что-то очень своеобразное. Более того, чтобы объяснить тот факт, что немедленно повторенное измерение дает тот же самый результат, мы вынуждены предположить, что акт измерения разрушает волновую функцию таким образом, который в лучшем случае трудно согласовать с нормальной эволюцией, предписанной уравнением Шредингера. В свете этого неудивительно, что многие поколения физиков отступили на позиции агностиков и советовали своим ученикам не тратить время на размышления о концептуальных основах теории.
В период становления копенгагенской интерпретации, которая была сколочена на скорую руку, многие не соглашались с постулированным существованием объективной случайности и с нелокальностью коллапса волновой функции. В последующих трактовках ортодоксальной интерпретации сошлись на нефизичности коллапса, а для решения многих проблем ввели декогеренцию — разрушение самосогласованного состояния при запутывании квантовых объектов. В частности, проблема с котом решилась тем, что механизм приводящий в действие машину смерти производит измерение квантовой системы, непреклонно вынуждая ее принять значение из спектра собственных чисел. Такое решение, по крайней мере, позволяет избежать отупляющего солипсизма Вигнера и других, которые убеждали себя, что именно вовлеченность человеческого сознания составляет измерение в квантовой механике. Частью проблемы является само слово «измерение» или «наблюдение», которое, безусловно, несет в себе намек на человеческое участие. Гейзенберг предложил слово «событие», которое, возможно, было бы предпочтительнее. Но ничего не поделаешь, термин устоялся и еще долго будет импонировать доморощенным упразднителям мирового заговора и бередить слух вовлеченных в тему. Касательно ЭПР и неравенств Белла можно будет поговорить уже в рамках интерпретаций. Конечно, чтобы развеять иллюзии и непонимание каждый должен сам пройти через тонны литературы и исписанных тетрадей. Да, довольно субъективно, но я испытал это на своей шкуре, от отторжения того что вдалбливают на лекциях и уверенности, что всем просто пудрят мозги, до получения формул совпадающих с результатами экспериментов. Будет сложно, но оно стоит того. Чтобы ни говорили про религиозные тексты (кстати, именно Библия убила во мне христианина), о том как они расставляют все на свои места и дают ответы на сокровенные вопросы, они не сравнятся с красотой математики различных формализмов, с хитросплетением связей разделов физики, с объяснительной мощью эволюционной теории и с простотой фундаментальных принципов, порождающих многообразие вселенских масштабов. Познание открывает взору все больше красоты окружающего мира. А разве не в этом состоит смысл жизни? Видео:В чем парадокс ЭФФЕКТА НАБЛЮДАТЕЛЯ? | Кот Шрёдингера и параллельные мирыСкачать  Опыт Штерна—ГерлахаМожно экспериментально доказать, что атомы и элементарные частицы обладают магнитными спинами, которые квантуются. Многие субатомные частицы обладают собственным угловым моментом (см. Закон сохранения момента импульса), который назвали спин. Обладающая электрическим зарядом и спином элементарная частица (например, электрон или протон) может, в таком случае, быть представлена в виде микроскопического циркулярного тока, который, в свою очередь, производит магнитный момент, связанный со спином, и заряженная частица ведет себя еще и как микроскопический магнит. Итак, и атомы, и элементарные частицы должны производить магнитные поля: первые — в силу циркуляции электронов на орбитах; вторые — в силу присущего им спина. Разумно предположить, что северный и южный полюса этих атомных и субатомных магнитов могут быть ориентированы произвольным образом. Постулаты квантовой механики, однако, такого произвола не допускают. Подобно всем иным свойствам частиц в мире квантовой физики, направление магнитного спина квантуется: во внешнем электромагнитном поле он может принимать только направления, относящиеся к фиксированному набору. Отто Штерн и Вальтер Герлах в 1921 году как раз и провели опыт, позволивший экспериментально подтвердить как наличие у атомов спина, так и факт его пространственного квантования. В основе их экспериментальной установки лежал мощный постоянный магнит, между близко расположенными полюсами которого образовывалось сильно неоднородное магнитное поле. Под воздействием такого поля частица, обладающая собственным магнитным моментом, обязана отклоняться в направлении, зависящем от ориентации ее магнитного спина. Если бы атом управлялся законами классической механики Ньютона (то есть, квантования спинов не наблюдалось бы), полюса микроскопических магнитов были бы ориентированы хаотичным образом, и они отклонялись бы во всевозможных направлениях. Где бы позади магнита мы ни разместили датчики, какие-то атомы обязательно отклонялись бы в этом направлении и попадали на них. Если же верна квантово-механическая гипотеза, и спины атомов и частиц квантуются, они будут отклоняться лишь в «разрешенных» направлениях и на разрешенные углы. В исходном эксперименте исследовались свойства именно атомов (сначала серебра, а затем и других металлов. — Прим. переводчика), и атомы некоторых веществ, как выяснилось, вообще отклоняются лишь в двух направлениях (условно говоря, «вверх» или «вниз» в зависимости от ориентации их магнитного спина «на север» или «на юг»). Позже уже одному Штерну удалось получить аналогичные результаты и для пучков протонов и электронов. Тем самым, этот опыт стал одним из главных подтверждений правильности постулатов квантовой механики.
Немецкий, затем американский физик. Родился в Зохрау (современный г. Жоры, Польша). Окончил Университет в Бреслау (современный Вроцлав). В 1921 году переехал во Франкфурт, где познакомился в уроженцем этого города и сотрудником местного университета Вальтером Герлахом (Walter Gerlach, 1889–1979), вместе с которым они в том же году и провели прославивший их опыт. В качестве профессора физической химии Гамбургского университета Штерн изучал магнитные свойства элементарных частиц, за что был удостоен Нобелевской премии по физике в 1943 году. К тому времени Штерн уже 10 лет жил и работал в Технологическом институте Карнеги в Питтсбурге (США), ведущим сотрудником которого оставался до конца своих дней. Мне хотелось бы провести модифицированный опыт Штерна-Герлаха, в котором атомный пучок отодвинут от плоскости симметрии магнитного поля на первом и втором магнитах. Я ожидаю, что в этом случае дочерний пучок перестанет расщепляться, что продемонстрирует работоспособность классической физики в масштабах микромира. Подробности: http://217.122.116.6/nanoworld/20041130/forum/astronom/as_p_ 019.htm Кто подскажет, в каком ВУЗе есть установка для повторени опыта Штрена-Герлаха? Желательно продублировать по email: nanoworld2003#yandex.ru (# -> @) Кушелев: -В процессе обсуждения были созданы макроскопические магнитные модели разных изомеров атома серебра. Модельный эксперимент показал, что достаточно снизить скорость атомов в оригинальном опыте Штерна-Герлаха, и пучок перестанет расщепляться. Подробности: http://nanoworld.pointclark.net/nanoworld/forums_copy/rassyl ka/index.htm Ширина пучка не является строго единичной (один атом). Атом является магнитом или намагничивается при пролете и в пучке ориентация при пролете любого по степени однородности поля распределена хаотически и в среднем может быть даже равномерна. Следовательно, притяжение к разным полюсам тоже должно происходить равномерно. Отсюда и симметричное расположение компонент. В поле магнита большинство атомов будет выправлять ориентацию к ближайшему полюсу, то есть ориентироваться соответствующим полюсом к ближайшему полюсному наконечнику и будет к нему притягиваться. Современная феноменология постоянных (да и вообще) магнитов совершенно не учитывает краевого эффекта у полюсных наконечников. На острых кромках (периферия полюсного наконечника) силы притяжения или отталкивания более значительны, чем в центральной плоской поверхности полюсного наконечника. Кстати, такой же эффект имеется и в электростатике. Во второй схеме пучок пропускался вдоль длинных полюсных наконечников. Один из них острый, а противоположный наконечник выполнен с прямоугольной канавкой посредине. Под углом ко входящему потоку расположил такие наконечники (разинув пасть) и три компоненты с превеликим удовольствием. Поближе сдвинул, вообще ни одной. резкая критика опыта Рудневым. автор правильно подметил время взаимодействия атома с полем, и дело еще и в этой квадратной выемке с двумя горбами. Отсюда именно растут ноги. Выводы: опыт решительно ничего не доказывает. Наоборот, является явной выдачей желаемого за действительное. Существование спина электрона таким образом под сомнением. И это еще мягко сказано. 🔥 ВидеоОпыт ШтернаСкачать  Опыт Штерна (анимация)Скачать  Квантовая механика 3 - Последовательное соединение приборов Штерна-ГерлахаСкачать  Урок 455. Уравнение ШрёдингераСкачать  Что такое спин?Скачать  Квантовая механика 29 - GHZ-экспериментСкачать  Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать  Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать  Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать  Тройные углы + Логарифмы. Смешанное уравнение. Ларин № 448Скачать  Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать  Эксперимент Штерна-Герлаха в эфирной теорииСкачать  Консультация по квантовой механике. Часть 7. "Спин электрона"Скачать  |
(и его магнитный момент 
) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рис. 7.10).
.
.
(проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.
(спина) и, соответственно, собственного магнитного момента электрона Pms.
, где s – спиновое квантовое число.
может иметь (2s + 1) различных ориентаций в магнитном поле.
, а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.
.
проекция спина 
квантуется (аналогично, как 
, то и 
). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением:
,
– магнитное спиновое квантовое число, 
, т.е. может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.
.
.
– спиновое гиромагнитное отношение.
. В квантовом случае это будет перевод операторов плотности. Свойство аффинности имеет прямой статистический смысл: оно означает сохранение «весов» в смесях состояний.
— афинное взаимно-однозначное отображение множества квантовых состояний S на себя, то есть, обратимую эволюцию. При обратимой эволюции чистые состояния переходят в чистые, при этом вектор исходного чистого состояния 
преобразуется в 
.
(однородность по времени)
можно получить уравнение Шредингера
> = hatleft|Psiright> $» data-tex=»display»/>
— гамильтониан, оператор полной энергии системы, то есть, сумма кинетической энергии 
и энергии системы в поле некоего потенциала.
-электрона в цепи полиена 
.
гамильтониан и волновая функция становятся:
