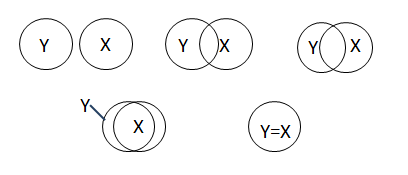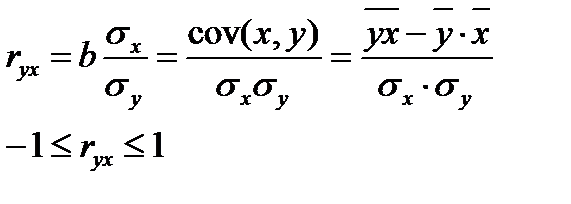Экономическая интерпретация параметров уравнения регрессии (6 видео)

Экономическая интерпретация коэффициента регрессии

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово-экономический институт

К.ф. – м.н., доцент кафедры: Василенко В.В.

Студент: Чмиль А.А., ФиК, 3 Курс

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (X, млн.руб.).

Xi	Yi
33	43
17	27
23	32
17	29
36	45
25	35
39	47
20	32
13	22
12	24

n	Xi	Yi	Yi*Xi	Xi2	Yi2	Y(xi)	Yi — Y(xi)	(Yi — Y(xi))2	A
1	33	43	1419	1089	1849	42,23428	0,765721183	0,5863289	1,78%
2	17	27	459	289	729	27,69234	-0,692335546	0,4793285	2,56%
3	23	32	736	529	1024	33,14556	-1,145564273	1,3123175	3,58%
4	17	29	493	289	841	27,69234	1,307664454	1,7099863	4,51%
5	36	45	1620	1296	2025	44,96089	0,03910682	0,0015293	0,09%
6	25	35	875	625	1225	34,96331	0,036692818	0,0013464	0,10%
7	39	47	1833	1521	2209	47,68751	-0,687507544	0,4726666	1,46%
8	20	32	640	400	1024	30,41895	1,581050091	2,4997194	4,94%
9	13	22	286	169	484	24,05685	-2,056849728	4,2306308	9,35%
10	12	24	288	144	576	23,14798	0,852021726	0,725941	3,55%
сумма	235	336	8649	6351	11986	336	0,00	12,019795	31,93%
средняя	23,5	33,6	864,9	635,1	1198,6	33,6	0,00	1,2019795	3,19%
δ	9,102198	8,345058	—	—	—	—	—	—	—
δ 2	82,85	69,64	—	—	—	—	—	—	—

Вспомогательная таблица для расчетов параметров линейной регрессии. Табл.2

Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

После проведенных расчетов линейная модель имеет вид:

Y = 12,24152 + 0,908871x , коэффициент регрессии составил 0,908871. Экономический смысл параметра регрессии заключается в следующем: с увеличением капиталовложений на 1 единицу выпуск продукции увеличивается на 0,908871 единиц.

Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков; построить график остатков.

Вычисленные остатки приведены в таблице 2. Остаточная сумма квадратов составила 12,02. Дисперсия остатков составила:

D_ост = ((Y- Yср.) 2 — (Y(xi) — Yср.) 2 )/ (n – 2) = 1,502474351.

График остатков. Рис.1

Проверить выполнение предпосылок МНК.

Остатки гомоскедастичны, автокорреляция отсутствует (корреляция остатков и фактора Х равна нулю, рис.1), математическое ожидание остатков равно нулю, остатки нормально распределены.

Корреляция остатков и переменной Х. Рис 2.

Осуществить проверку значимости параметров уравнения регрессии с помощью t – критерия Стьюдента (α = 0,05).

Найдем стандартную ошибку коэффициента регрессии:

mb = (Dост. / ∑(x – xср.) 2 ) ½ = 0,042585061

Теперь проведем оценку значимости коэффициента регрессии:

tb = b / mb= 21,3424949

При α = 0,05 и числе степеней свободы (n – 2) tтабл. = 2,3060. Так как фактическое значение t – критерия больше табличного, то гипотезу о несущественности коэффициента можно отклонить. Доверительный интервал для коэффицента регрессии определяется как b ± t* mb. Для коэффициента регрессии b границы составят: 0,908871 – 2,3060*0,042585061 ≤ b ≤ 0,908871+2,3060*0,042585061

0,81067 ≤ b ≤ 1,0070722

Далее определим стандартную ошибку параметра a:

m_a = (Dост.*( ∑x 2 / (n*∑(x – xср.) 2 )) 1/2 = 1,073194241

Мы видим, что фактическое значение параметра а больше, чем табличное, следовательно, гипотезу о несущественности параметра а можно отклонить. Доверительный интервал составит: a± t* ma. Границы параметра составят:

9,766735 ≤ a ≤14,716305

Проверим значимость линейного коэффициента корреляции на основе ошибки коэффициента корреляции:

m_r = ((1 – r 2 ) / (n – 2)) 1/2 = 0,046448763

Фактическое значение t – критерия Стьюдента определяется:

t_r = (r / (1 – r 2 )) * (n – 2) 1/2 = 21,3424949

Значение t_r фактическое больше табличного, следовательно при уровне значимости α = 0,05 и степени свободы (n – 2), коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.

Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью f – критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

R 2 = Rxy 2 = 0,98274 – детерминация.

F = (R 2 /(1 – R 2 ))*((n – m – 1)/m) = 455,5020887

Fтабл. 5,32 2 / ∑(x – x_ср ) 2 ) 1/2 = 1,502474351*(1+(1/10)+ ((31,2 – 23,5) 2 / 828,50)) 1/2 = 1,6262596 млн.руб.

Предельная ошибка прогноза, которая в 90% случаев не будет превышена, составит:

Доверительный интервал прогноза:

γ_ур _min = 40,598295 – 3,7501546 = 36,848141 млн.руб.

γ_ур _max = 40,598295 + 3,7501546 = 44,348449 млн.руб.

Среднее значение показателя составит:

Y_p = (36,848141 + 44,348449) / 2 = 40,598295 млн.руб.

Представить графически фактические и модельные значения Y точки прогноза

График фактических и прогнозируемых параметров. Рис.3

Составить уравнения нелинейной регрессии:

Построить графики построенных уравнений регрессии.

Y(x) = 54,1842 + (-415,755) * 1/x – гиперболическое уравнение регрессии.

Y(x) = 4,746556 * X 0,625215 – степенное уравнение регрессии.

Y(x) = 17,38287 * 1,027093 X показательное уравнение регрессии.

Графикимоделей представлены ниже на рисунках 4,5 и 6.

Для указанных моделей найти коэффициенты детерминации, коэффициент эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.

Коэффициенты (индексы) детерминации:

R 2 _показ = R_xy = 0,959136358

Э_гип = -b / (a * x + b) = 0,484804473

Э_степ = b = 0,625215

Э_показ = x * lnb = 0,628221

Средние относительные ошибки аппроксимации:

А = 1/n * ∑ |y – y_xi | * 100%

Как мы видим, степенная регрессия наиболее интересна в экономическом смысле, потому что у нее самый низкий показатель средней ошибки аппроксимации, самый высокий показатель эластичности и детерминации. Это говорит о том, что у степенной регрессионной модели высокое качество, она предлагает наибольшую прибыль и более зависима от фактора Х (капиталовложений).

Список использованной литературы

1. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курашева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 192.: ил.

2. Эконометрика. Учебник для вузов.; Под ред. чл. – кор. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344.

Содержание

Экономическая интерпретация параметров модели
Интерпретация уравнения регрессии
Интерпретация уравнения регрессии
📹 Видео

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

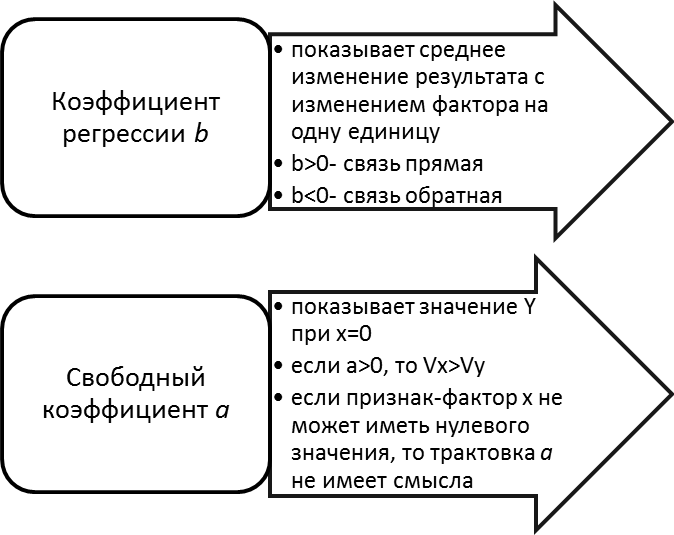
Экономическая интерпретация параметров модели

Рис. 4.1. Интерпретация параметров модели

Коэффициенты корреляции и детерминации в линейной модели парной регрессии. Если все точки лежат на построенной прямой, то регрессия Y на Х «идеально» объясняет поведение зависимой переменной. Обычно поведение Y лишь частично объясняется влиянием переменной Х.

Рис. 4.2. Диаграмма Венна

Линейный коэффициент парной корреляции:

Если b>0, то r_yx>0; если b 2 – остаточная дисперсия на одну степень свободы;

t – случайная величина, имеющая распределение Стьюдента с заданной вероятностью.

Вопросы и задания для самоконтроля

1. Каков экономический смысл коэффициента регрессии?

2. Какой смысл может иметь свободный коэффициент уравнения регрессии?

3. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?

4. Каков статистический смысл коэффициента детерминации?

5. Как записывается баланс для сумм квадратов отклонений результативного признака?

6. Что происходит, когда общая СКО равна остаточной? В каком случае общая СКО равна факторной?

7. Что такое число степеней свободы? Чему равны числа степеней свободы для различных СКО в парной регрессии?

8. Как используется F-статистика в регрессионном анализе?

9. Как F-статистика связана с коэффициентом детерминации в парной регрессии?

10. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?

11. В чем суть предсказания индивидуальных значений зависимой переменной?

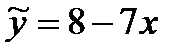
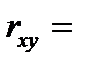
Задача 1. Пусть имеется следующая модель парной регрессии, построенная по 20 наблюдениям: . При этом — 0,5.

Задание: построить доверительный интервал для коэффициента регрессии в этой модели с вероятностями 0,9 и 0,95.

Задача 2. Анализируется зависимость между доходами горожан (X), имеющими индивидуальные домовладения, и рыночной стоимостью их домов (Y). По случайной выборке из 120 горожан данной категории получены результаты:

27343; 115870; 75200;

1620340; 250431.

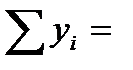
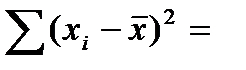
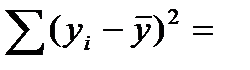
Задание: найти оценку коэффициента регрессии и построить 95% доверительный интервал для коэффициента регрессии.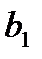

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Интерпретация уравнения регрессии

Видео:Эконометрика. Линейная парная регрессияСкачать

Интерпретация уравнения регрессии

Интерпретация регрессионных уравнений Существует два этапа интерпретации уравнения регрессии. Первый этап Уточнить, потому что уравнения интерпретируются устно Тот, кто не является статистиком. Во вторых это Нет необходимости решать, делать это или больше. Тщательное исследование зависимости. Оба этапа очень важны.

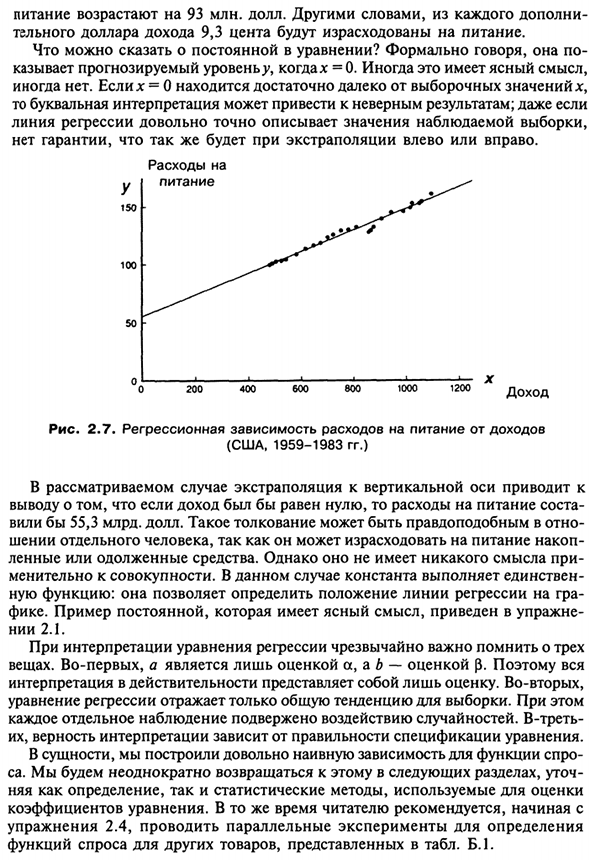
На втором этапе мы рассмотрим несколько поз А пока давайте обратим основное внимание на первый этап. Это объясняет Определяется регрессионной моделью функции спроса, то есть регрессией между расами Потребители переходят на еду (у) и располагаемый личный доход (х) Данные Отображается в графическом формате (рисунок 2.7). Предположим, что истинная модель описывается y = a + $ x + u, (2,41) И регрессионная оценка £ = 55,3 + 0,093 *. (2,42)

Данные приведены в таблице. Б.1 в США за период с 1959 по 1983 год. Людмила Фирмаль

Полученные результаты можно интерпретировать следующим образом: коэффициент в х (коэффициент градиента) Единица у увеличивается на 0,093 единицы. х и у оба измеряются в мил Миллиарды долларов по фиксированной цене. Поэтому склон Если выручка увеличится на 1 миллиард долларов, 64 Питательные вещества увеличились на 93 миллиона долларов.

Это значит Из реальных долларовых доходов 9,3 цента тратятся на еду. Как насчет констант уравнения? Формально она Если x = 0, указывает уровень прогнозирования ^. Это ясно имеет смысл. Иногда нет. Если х = 0 достаточно далеко от значения выборки х, В этом случае буквальная интерпретация может привести к неверным результатам.

Даже если Линия регрессии является очень точным представлением наблюдаемого значения выборки. Нет гарантии, что то же самое произойдет с экстраполяцией влево или вправо. в 150 грамм 100 грамм 50 Стоимость пища 200 400 600 800 —100 • ”0 120—0 X доходов Рисунок 2.7. Зависимость расходов на питание от дохода (США, 1959-1983).

В рассматриваемом случае путем экстраполяции на вертикальную ось Если доход равен нулю, стоимость еды Сделал бы 55,3 миллиарда долларов. Такое толкование может быть правдоподобным в отношении Лица, которые могут тратить накопления пищи Кредиты или заемные средства. Тем не менее, это не имеет смысла, если По отношению ко всему.

В этом случае константа сделает единственное Функция: может определить положение линии регрессии на графике Поддельный. Примеры констант с ясным значением приведены в упражнении. Институт 2.1. При интерпретации уравнений регрессии очень важно помнить три Вещь. Во-первых, a является только оценкой a, а a b является оценкой (3. Интерпретация на самом деле просто оценка.

Во-вторых Уравнение регрессии отражает только общую тенденцию выборки. В то же время Индивидуальные наблюдения подвержены случайности. третий В этих случаях точность интерпретации зависит от точности спецификации уравнения. По сути, мы построили довольно простую зависимость от функции спроса Мы вернемся к этому в следующем разделе и уточнить.

Определяя как определения, так и статистические методы, используемые при измерении Коэффициент уравнения. В то же время читателям рекомендуется начать с Упражнение 2.4, определить путем проведения параллельных экспериментов Функция спроса на другие товары приведена в таблице. B.1. После оценки регрессии возникают следующие вопросы:

Есть ли способ определить точность оценки? Это очень важно Рост будет обсуждаться в следующем разделе. Сначала рассмотрим дальше Подробно объясните роль остаточного члена и его влияние на оценки a и p. Интерпретация уравнений линейной регрессии.

Представьте себе простой способ интерпретации линейных коэффициентов. Людмила Фирмаль

Уравнение регрессии у = а + бх Если есть простая естественная единичная переменная Измерение. Сначала увеличим х на 1 единицу ( Единица переменной х) увеличивается у в б (единица переменной у). Второй этап Проверка того, что собой представляет хна на самом деле, Замените слово «единица измерения» на фактическое количество.

Третий этап Проверка возможности более простого выражения результата Это может быть не очень удобно. В примере В этом разделе указана единица измерения для х и у Потому что миллиарды долларов были потрачены, Замечательное упрощение. Константа а дает предсказанное значение у (единица ^). х = 0 Это может иметь или не иметь смысла в зависимости от значения Конкретная ситуация. Упражнение 1 2.1.

Регрессия стоимости продуктов питания (на основе того же Данные, для которых уже описана функция спроса, описанная в тексте) Меню определено как f = 1 в 1959 году, t = 2 в 1960 году и т. Д. Нини: у = 95,3 + 2,53 /. Интерпретация в Сравнение результатов оценки регрессии с аналогом Аналогичные результаты для модели регрессии функции спроса Пожалуйста, смотрите текст.

В этом случае постоянная Есть простая интерпретация. 2.2. Регрессивная зависимость от одноразовой зависимости стоимости жилья 1 Упражнение 2.4 особенно важно в том смысле, что оно запускает серию регрессий для развлечения. Общий спрос. Это оценивается читателем на протяжении всей книги.

Если это упражнение Если это делается группой студентов, учитель должен дать студентам задания Товарные. Более подробная информация о доступных данных доступна в Приложении B.go Личный доход в соответствии с таблицей. B.1, оба количества Можно оформить миллиарды долларов с 1959 по 1983 В следующем формате: j> = -27,6 + 0,178х.

Регрессивная зависимость и определение стоимости жилья с течением времени То же самое, что и упражнение 2.1, можно выразить как: f = 48,9 + 4,84 г. Вот экономическая интерпретация этих регрессий. У них разные предложения Описание тех же данных в переменной y. Сколько они Вы можете согласиться? 2,3.

Создайте уравнение регрессии между p и e из данных упражнения 1.3, сначала используйте все 12 наблюдений, затем исключите наблюдения 1. Дает экономическую интерпретацию для Японии. 2,4. В таблице. B.1 — потребительские расходы США располагаемый личный доход за период 1959-1983 гг. Назовите один продукт — не еду, а не домашнюю Пропустите регрессию между y и x. х — располагаемый личный доход, использующий Данные за 25 лет.

Интерпретация коэффициентов регрессии 2.5. Таким образом, регрессия между характеристиками продукта и временем Мы сделаем это в упражнении 2.1. Правильная интерпретация и сравнение У нее есть интерпретация регрессии, полученная в упражнении 2.4. 2.6. Два человека строят один и тот же набор временных тенденций 25 наблюдений за переменной y с использованием модели: у = а + р / + и

Где t — время (принимает значения непрерывно от 1 до 25), а -case Член чаепития. Получите первое уравнение: j> = 6,70 + 1,79 /. Вторая по ошибке оценивает регрессию между / и у и этим уравнением По мнению: t = -0,25 + 0,44 >>. Из этого уравнения он получает: у = 0,57 + 2,27 /. Объясните это уравнение и несоответствие между уравнениями, Получено первым исследователем. 2,7.

Как изменяется регрессионный балл в упражнении 2.1 Фактическая дата (1959-1983) используется как / вместо числа из 1 до 25? 2,8. Исследователи, 1 Не начинайте сначала вычислять коэффициент регрессии. Заполнены большинство арифметических расчетов в упражнении 1.3. 2 Учителя являются учениками, если это групповое занятие.

Удар, чтобы дать задачу оценки регрессии различных видов товаров в дополнение к еде жилья.люги, основанные на данных АМЕ (у) и общем располагаемом личном доходе (х) Риканская экономика (обе измеряются в миллиардах долларов) Фиксированная цена) с использованием данных и модели временных рядов за год: y = a + px + u. 1.

Исследователь выполняет регрессионный анализ, чтобы получить уравнение. Используйте обычный метод наименьших квадратов. Если предположить, что Обе ценности могут быть значительно недооценены внутренней системой Личные счета за желание людей не платить налоги Правительство, исследователи принимают два альтернативных улучшения Недооцененная оценка. 2.

Исследователи добавляют $ 90 млрд к показателю каждый год >> и Показатель х 200 миллиардов долларов. 3. Исследователь увеличивает x и y на 10% Каждый год. Оценить влияние корректировок (2) и (3) на результаты рег. ressii. 2.9. Исследователи имеют общие годовые данные временных рядов.

Заработная плата (W), валовой доход (P) и валовой доход (Y) Для страны сроком на n лет. По определению Y = W + T1. Получите регулярное уравнение, используя метод наименьших квадратов Рссии: fr = a0 + aiY; ft = Z> 0 + bxY. Указывает, что коэффициент регрессии автоматически удовлетворяет Следующее уравнение: но х + * я = 1; * o + K = 0. Интуитивно объясните, почему так должно быть. 2.10.

Исследователи не имеют нестохастической части истинной модели у пропорционально х. y = $ x + u. Исходя из исходного принципа, выведите формулу b, оценка МНК б. В этом случае (2.31) указывает, что это можно записать следующим образом. S = bj] + b2J, xj -2 £ Xx,. > 7 Для этого b = 2, xiyi / Zxf. 2,11. Выведите оценку наименьших квадратов модели из первого предположения. у = а + у. 68 То есть у это просто сумма констант Случайные участники с нами. Сначала переопределите 5, а затем дифференцируйте Цитирование.