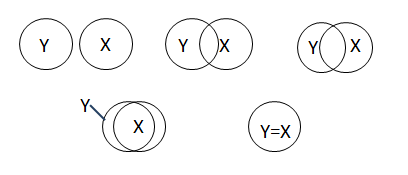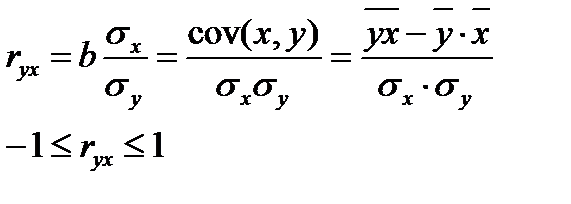Федеральное агентство по образованию ГОУ ВПО
Всероссийский заочный финансово-экономический институт
К.ф. – м.н., доцент кафедры: Василенко В.В.
Студент: Чмиль А.А., ФиК, 3 Курс
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (X, млн.руб.).
| Xi | Yi |
| 33 | 43 |
| 17 | 27 |
| 23 | 32 |
| 17 | 29 |
| 36 | 45 |
| 25 | 35 |
| 39 | 47 |
| 20 | 32 |
| 13 | 22 |
| 12 | 24 |
| n | Xi | Yi | Yi*Xi | Xi2 | Yi2 | Y(xi) | Yi — Y(xi) | (Yi — Y(xi))2 | A |
| 1 | 33 | 43 | 1419 | 1089 | 1849 | 42,23428 | 0,765721183 | 0,5863289 | 1,78% |
| 2 | 17 | 27 | 459 | 289 | 729 | 27,69234 | -0,692335546 | 0,4793285 | 2,56% |
| 3 | 23 | 32 | 736 | 529 | 1024 | 33,14556 | -1,145564273 | 1,3123175 | 3,58% |
| 4 | 17 | 29 | 493 | 289 | 841 | 27,69234 | 1,307664454 | 1,7099863 | 4,51% |
| 5 | 36 | 45 | 1620 | 1296 | 2025 | 44,96089 | 0,03910682 | 0,0015293 | 0,09% |
| 6 | 25 | 35 | 875 | 625 | 1225 | 34,96331 | 0,036692818 | 0,0013464 | 0,10% |
| 7 | 39 | 47 | 1833 | 1521 | 2209 | 47,68751 | -0,687507544 | 0,4726666 | 1,46% |
| 8 | 20 | 32 | 640 | 400 | 1024 | 30,41895 | 1,581050091 | 2,4997194 | 4,94% |
| 9 | 13 | 22 | 286 | 169 | 484 | 24,05685 | -2,056849728 | 4,2306308 | 9,35% |
| 10 | 12 | 24 | 288 | 144 | 576 | 23,14798 | 0,852021726 | 0,725941 | 3,55% |
| сумма | 235 | 336 | 8649 | 6351 | 11986 | 336 | 0,00 | 12,019795 | 31,93% |
| средняя | 23,5 | 33,6 | 864,9 | 635,1 | 1198,6 | 33,6 | 0,00 | 1,2019795 | 3,19% |
| δ | 9,102198 | 8,345058 | — | — | — | — | — | — | — |
| δ 2 | 82,85 | 69,64 | — | — | — | — | — | — | — |
Вспомогательная таблица для расчетов параметров линейной регрессии. Табл.2
Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
После проведенных расчетов линейная модель имеет вид:
Y = 12,24152 + 0,908871x , коэффициент регрессии составил 0,908871. Экономический смысл параметра регрессии заключается в следующем: с увеличением капиталовложений на 1 единицу выпуск продукции увеличивается на 0,908871 единиц.
Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков; построить график остатков.
Вычисленные остатки приведены в таблице 2. Остаточная сумма квадратов составила 12,02. Дисперсия остатков составила:
Dост = ((Y- Yср.) 2 — (Y(xi) — Yср.) 2 )/ (n – 2) = 1,502474351.
График остатков. Рис.1
Проверить выполнение предпосылок МНК.
Остатки гомоскедастичны, автокорреляция отсутствует (корреляция остатков и фактора Х равна нулю, рис.1), математическое ожидание остатков равно нулю, остатки нормально распределены.
Корреляция остатков и переменной Х. Рис 2.
Осуществить проверку значимости параметров уравнения регрессии с помощью t – критерия Стьюдента (α = 0,05).
Найдем стандартную ошибку коэффициента регрессии:
mb = (Dост. / ∑(x – xср.) 2 ) ½ = 0,042585061
Теперь проведем оценку значимости коэффициента регрессии:
tb = b / mb= 21,3424949
При α = 0,05 и числе степеней свободы (n – 2) tтабл. = 2,3060. Так как фактическое значение t – критерия больше табличного, то гипотезу о несущественности коэффициента можно отклонить. Доверительный интервал для коэффицента регрессии определяется как b ± t* mb. Для коэффициента регрессии b границы составят: 0,908871 – 2,3060*0,042585061 ≤ b ≤ 0,908871+2,3060*0,042585061
0,81067 ≤ b ≤ 1,0070722
Далее определим стандартную ошибку параметра a:
ma = (Dост.*( ∑x 2 / (n*∑(x – xср.) 2 )) 1/2 = 1,073194241
Мы видим, что фактическое значение параметра а больше, чем табличное, следовательно, гипотезу о несущественности параметра а можно отклонить. Доверительный интервал составит: a± t* ma. Границы параметра составят:
9,766735 ≤ a ≤14,716305
Проверим значимость линейного коэффициента корреляции на основе ошибки коэффициента корреляции:
mr = ((1 – r 2 ) / (n – 2)) 1/2 = 0,046448763
Фактическое значение t – критерия Стьюдента определяется:
tr = (r / (1 – r 2 )) * (n – 2) 1/2 = 21,3424949
Значение tr фактическое больше табличного, следовательно при уровне значимости α = 0,05 и степени свободы (n – 2), коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью f – критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
R 2 = Rxy 2 = 0,98274 – детерминация.
F = (R 2 /(1 – R 2 ))*((n – m – 1)/m) = 455,5020887
Fтабл. 5,32 2 / ∑(x – xср ) 2 ) 1/2 = 1,502474351*(1+(1/10)+ ((31,2 – 23,5) 2 / 828,50)) 1/2 = 1,6262596 млн.руб.
Предельная ошибка прогноза, которая в 90% случаев не будет превышена, составит:
Доверительный интервал прогноза:
γур min = 40,598295 – 3,7501546 = 36,848141 млн.руб.
γур max = 40,598295 + 3,7501546 = 44,348449 млн.руб.
Среднее значение показателя составит:
Yp = (36,848141 + 44,348449) / 2 = 40,598295 млн.руб.
Представить графически фактические и модельные значения Y точки прогноза
График фактических и прогнозируемых параметров. Рис.3
Составить уравнения нелинейной регрессии:
Построить графики построенных уравнений регрессии.
Y(x) = 54,1842 + (-415,755) * 1/x – гиперболическое уравнение регрессии.
Y(x) = 4,746556 * X 0,625215 – степенное уравнение регрессии.
Y(x) = 17,38287 * 1,027093 X показательное уравнение регрессии.
Графикимоделей представлены ниже на рисунках 4,5 и 6.
Для указанных моделей найти коэффициенты детерминации, коэффициент эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.
Коэффициенты (индексы) детерминации:
R 2 показ = Rxy = 0,959136358
Эгип = -b / (a * x + b) = 0,484804473
Эстеп = b = 0,625215
Эпоказ = x * lnb = 0,628221
Средние относительные ошибки аппроксимации:
А = 1/n * ∑ |y – yxi | * 100%
Как мы видим, степенная регрессия наиболее интересна в экономическом смысле, потому что у нее самый низкий показатель средней ошибки аппроксимации, самый высокий показатель эластичности и детерминации. Это говорит о том, что у степенной регрессионной модели высокое качество, она предлагает наибольшую прибыль и более зависима от фактора Х (капиталовложений).
Список использованной литературы
1. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курашева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 192.: ил.
2. Эконометрика. Учебник для вузов.; Под ред. чл. – кор. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344.
Видео:Парная регрессия: линейная зависимостьСкачать

Задача
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков S2ε ; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью f-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составит 80% от его максимального значения.
7. Представить графически фактическое и модельное значение Y точки прогноза.
8. Составить уравнения нелинейной регрессии:
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Задача 1. Уравнение линейной регрессии имеет вид: 


С помощью ППП Excel найдем параметры уравнения линейной регрессии. Порядок выселения следующий:
1. Активизируем инструмент Пакет анализа:
1.1. Сервис →Настройки;
1.2. В диалоговом окне Настройки отметим пункт Пакет анализа→ ОК.
2. Ведем исходные данные;
Рис. 1. Исходные данные
3. Сервис → Анализ данных → Регрессия→ОК;
4. Заполним диалоговое окно ввода данных и параметров вывода:
Рис. 2. Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных представлены на рис. 3.
Рис. 3. Результат применения инструмента Регрессия
В ячейках В17 и В18 расположены значения параметров а и b соответственно. Итак, уравнение регрессии имеет вид: 
Коэффициент регрессии b показывает, что с ростом капиталовложений на 1 млн. руб. выпуск продукции увеличивается в среднем на 2,40 млн. руб.
Задача 2. Остатки определяются по формуле: 

На рис. 3. в ячейках С25:С34 уже вычислены остатки. А остаточную сумму квадратов найдем с помощью ППП Excel, использую функцию ПРОИЗВЕД. Результаты вычислений приведены на рис. 6.
Рис. 4. Остаточная сумма квадратов
Итак, остаточная сумма квадратов равна 25,96– она также вычислена с помощью Регрессии (ячейка D13).
Дисперсия остатков определяется по формуле: 
Поскольку остаточная сумма квадратов вычислена и равна 25,96, а количество наблюдений 10, то можно найти дисперсию остатков. Результат вычисления приведен на рис. 4 в ячейке В37.
Итак, дисперсия остатков составляет 25,96 (она также вычислена с помощью Регрессии – рис. 3, ячейка D13).
График остатков уже построен с помощью инструмента Анализа данных Регрессия (рис. 3). Приведем график остатков в отдельный вид.
Рис. 5. График остатков
Задача 3. Проверим выполнение предпосылок МНК. Свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей. Для того чтобы МНК давал наилучшие результаты, должны выполняться условия Гаусса — Маркова.
Условие 1. Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю: М(εi)=0.
В нашем случае уравнение регрессии включает постоянный член и, следовательно, это условие выполняется автоматически.
Условие 2. Случайная составляющая (εi) или зависимая переменная (yi)есть величины случайные, а независимая величина (xi)– величина неслучайная: 
Р — число поворотных точек. В нашем примере Р=6.




Р> 2,99; т. е. 6>2,99. Следовательно, условие выполняется.
Итак, случайная составляющая (εi) или зависимая переменная (yi) есть величины случайные.
Условие 3. Случайная переменная в любых двух наблюдениях независима.
Чтобы проверить выполнение данного условия, с помощью ППП Excel вычислим dw-критерий Дарбина — Уотсона: 
Т. к. остатки и остаточная сумма квадратов уже вычислены (рис. 5),то для нахождения dw-критерий Дарбина – Уотсона нужно найти (εi-εi-1) и (εi-εi-1)2.
Рис. 6. Вычисление dw-критерия Дарбина-Уотсона
Итак, dw=1,70. Поскольку dw > d2 (d2 = 1,36) , но dw tтабл и tb>tтабл, то параметры a и b уравнения регрессии значимы.
Осуществим проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,1) с помощью функции СТЬЮДРАСПОБР.
Рис. 16. Результат вычисления tтабл (α=0,1)
Итак, табличное значение t-критерия при уровне значимости и степенях свободы составляет 1,. Так как tа>tтабл и tb>tтабл, то параметры a и b уравнения регрессии значимы.
Задача 5. В случае линейной зависимости между переменными парный коэффициент корреляции является показателем тесноты связи и определяется по формуле:

Коэффициент корреляции в нашем примере уже вычислен с помощью инструмента Excel Регрессии (рис. 3, стр. 4) – ячейка В4, который равен 0,98405.
По шкале Чеддока коэффициент корреляции попал в интервал от 0,9 до 1, следовательно, это говорит о весьма высокой связи.
Долю дисперсии, объясняемую регрессией в общей дисперсии результативного признака y, характеризует коэффициент детерминации:

Коэффициент детерминации в нашем примере уже вычислен с помощью инструмента анализа Регрессии (рис. 3, ячейка В5) и составляет 0,96836.
Значимость уравнения регрессии y=13,89+2,40x определяется с помощью F-критерия Фишера (α=0,05) используя данную формулу: 

Табличное значение F-критерия Фишера при доверительной вероятности 0,05 при ν1=1 и ν2=8 уже вычислено с помощью функции FРАСПОБР и составляет 5,31766. Поскольку Fрасч>F табл, уравнение регрессии следует признать значимым.
Коэффициент эластичности для линейной функции определяется по формуле:

Таким образом, 
Это значит, что если фактор измениться на 1%, то в среднем на 0,87% измениться результат.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют относительную ошибку аппроксимации:

Вычислим относительную ошибку аппроксимации с помощью Excel.
Рис.17. Результаты вычислений относительной ошибки аппроксимации
Итак, относительная ошибка аппроксимации составила 3,86%, что говорит о качественной модели.
Задача 6. Осуществим прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если известно, что прогнозное значение фактора Х составит 80% от его максимального значения.
Прогнозное значение переменной y получается при подстановке в уравнение регрессии ожидаемого значения x: 

В нашем случае 

Вероятность реализации точечного прогноза равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большей надежностью. Доверительные интервалы зависят от стандартной ошибки, удаления 



Ширина доверительного интервала определяется по формуле:

Величина 

Рис. 18. Дополнительные расчеты

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

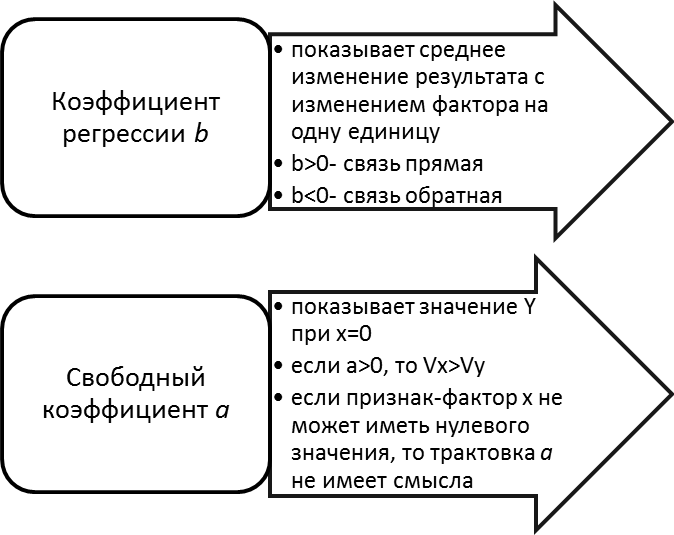
Экономическая интерпретация параметров модели
Рис. 4.1. Интерпретация параметров модели
Коэффициенты корреляции и детерминации в линейной модели парной регрессии. Если все точки лежат на построенной прямой, то регрессия Y на Х «идеально» объясняет поведение зависимой переменной. Обычно поведение Y лишь частично объясняется влиянием переменной Х.
Рис. 4.2. Диаграмма Венна
Линейный коэффициент парной корреляции:
Если b>0, то ryx>0; если b 2 – остаточная дисперсия на одну степень свободы;
t – случайная величина, имеющая распределение Стьюдента с заданной вероятностью.
Вопросы и задания для самоконтроля
1. Каков экономический смысл коэффициента регрессии?
2. Какой смысл может иметь свободный коэффициент уравнения регрессии?
3. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?
4. Каков статистический смысл коэффициента детерминации?
5. Как записывается баланс для сумм квадратов отклонений результативного признака?
6. Что происходит, когда общая СКО равна остаточной? В каком случае общая СКО равна факторной?
7. Что такое число степеней свободы? Чему равны числа степеней свободы для различных СКО в парной регрессии?
8. Как используется F-статистика в регрессионном анализе?
9. Как F-статистика связана с коэффициентом детерминации в парной регрессии?
10. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?
11. В чем суть предсказания индивидуальных значений зависимой переменной?
Задача 1. Пусть имеется следующая модель парной регрессии, построенная по 20 наблюдениям: 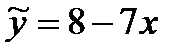
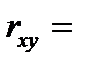
Задание: построить доверительный интервал для коэффициента регрессии в этой модели с вероятностями 0,9 и 0,95.
Задача 2. Анализируется зависимость между доходами горожан (X), имеющими индивидуальные домовладения, и рыночной стоимостью их домов (Y). По случайной выборке из 120 горожан данной категории получены результаты:

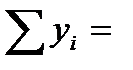
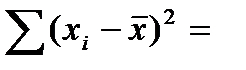
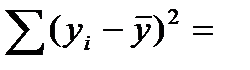

Задание: найти оценку коэффициента регрессии 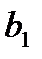
🎬 Видео
Эконометрика. Линейная парная регрессияСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Математика это не ИсламСкачать

Множественная регрессияСкачать

Лекция №1 "Основания термодинамики" (Попов П.В.)Скачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

СЕРДЦЕ: Потенциал действия кардиомиоцитовСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Что такое КВАНТОВЫЙ компьютер? | РАЗБОРСкачать

Математика #1 | Корреляция и регрессияСкачать

Множественная регрессия в ExcelСкачать

Как спрос и предложение задают ценыСкачать

Линейная регрессияСкачать