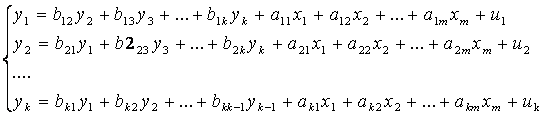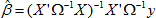Двухшаговый метод наименьших квадратов применим для решения системы одновременных уравнений (5 видео)

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Содержание

Проблема идентификации
Правила идентификации
Двухшаговый метод наименьших квадратов
Двухшаговый метод наименьших квадратов применим для решения только сверхидентифицируемой системы одновременных уравнений
Ваш ответ
решение вопроса
Похожие вопросы
Метод наименьших квадратов
Двухшаговый МНК. Системы одновременных уравнений
Взвешенный МНК
Доступный обобщенный МНК
📹 Видео

Видео:Двухшаговый метод наименьших квадратов в парной регрессииСкачать

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Двухшаговый метод наименьших квадратов

Если система сверхидентифицируема, то КМНК не используется, так как он не дает однозначных оценок для параметров структурной формы.

Для нахождения коэффициентов сверхиндифицируемых уравнений применяется двухшаговый МНК (ДМНК).

Двухшаговый МНК состоит в следующем.

1. Составляют приведенную форму модели и определяют значения коэффициентов для каждого ее уравнения в отдельности с помощью обычного МНК.
2. Выявляют эндогенные переменные, находящиеся в правой части структурного уравнения (коэффициенты которого определяют двухшаговым МНК), и находят их расчетные значения по полученным на первом этапе соответствующим уравнениям приведенной формы модели.
3. С помощью обычного МНК находят коэффициенты каждого структурного уравнения в отдельности, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, находящихся в правой части данного структурного уравнения, полученные на втором этапе.

Сверхидентифицируемая структурная модель может быть двух типов:

1) все уравнения системы сверхидентифицируемы;
2) система содержит наряду со сверхидентифицируемыми уравнениями и точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Применим ДМНК к простейшей сверхидентифицируемой модели

Эта модель может быть получена из идентифицируемой модели

если наложить ограничения на ее параметры, а именно b_vl = я_п. В результате первое уравнение стало сверхидентифицируемым: Н = 1 (у_<), D = 1 (дг₂), т.е. Н — 1 ₂ + и₂ подставим значения .г, и х₂ (в примере 11.7 это отклонения от средних уровней). Оценки для эндогенной переменной у₂ приведены в табл. 11.3.

Видео:Вычислительная математика 6 Метод наименьших квадратовСкачать

Двухшаговый метод наименьших квадратов применим для решения только сверхидентифицируемой системы одновременных уравнений

Видео:Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Ваш ответ

Видео:Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

решение вопроса

Видео:11 4 Применение МНК к решению систем линейных уравненийСкачать

Метод наименьших квадратов

Метод наименьших квадратов (МНК) — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Данный метод применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

При применении МНК используется подстановка в начальные уравнения неизвестных величин. При этом в правых частях уравнений получаются если не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.

Видео:Метод наименьших квадратов (МНК)Скачать

Двухшаговый МНК. Системы одновременных уравнений

Система одновременных уравнений — это система уравнений, содержащая взаимозависимые переменные, которые включены в одно из уравнений модели в качестве результативного признака, а в другие уравнения — в качестве факторного признака. Коэффициенты системы одновременных уравнений нельзя определить обычным МНК, так как правая часть системы одновременных уравнений содержит эндогенные переменные. Наиболее распространенным методом для расчета является двухшаговый метод наименьших квадратов (ДМНК).

ДМНК состоит в следующем:

составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;

выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют ДМНК, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели;

обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.

ДМНК производит оценку коэффициентов заданного регрессионного уравнения: y = Y · a + X · b + u .

y . Зависимая переменная уравнения;

Y . Матрица n * g наблюдений над другими значениями эндогенных переменных, входящих в уравнение;

X . Матрица n * k наблюдений над предопределёнными переменными, входящими в уравнение;

a . Вектор g *1 структурных коэффициентов, относящихся к переменным из матрицы Y ;

b . Вектор k *1 коэффициентов, относящихся к переменным из матрицы X ;

u . Вектор n *1 случайных возмущений.

Видео:Численные методы: Метод наименьших квадратовСкачать

Взвешенный МНК

Метод применяется для оценивания коэффициентов модели y = X β + e , минимизирующей сумму квадратов отклонений e’e . Оценивание выполняется по формуле β = ( X’X ) -1 X’Y .

При этом особо рассматривается случай мультиколлинеарности, когда матрица X’X близка к вырожденной (абсолютная величина определителя мала). В этих случаях оценка коэффициентов неоднозначна вследствие линейной зависимости столбцов матрицы X . Для получения однозначной оценки исключаем столбцы из матрицы X до тех пор, пока она не станет иметь максимальный ранг.

Взвешивание применяется для оценивания коэффициентов модели Y = X β + ε в предположении гетероскедастичности остатков .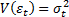

Случай сводится к стандартной модели множественной линейной регрессии с гомоскедастичными остатками несложным преобразованием:

Оценивание полученной модели выполняется стандартным МНК.

Видео:Метод наименьших квадратов. ТемаСкачать

Доступный обобщенный МНК

В случае линейной регрессионной модели Y = X β + ε в предположении распределения остатков ε по закону N (0, σ 2 Ω) с заданной матрицей ковариаций Ω, оценка доступного обобщенного метода наименьших квадратов реализуется формулой: