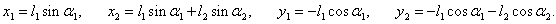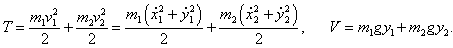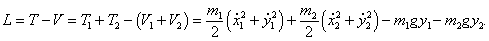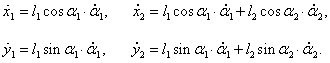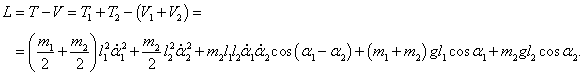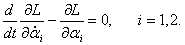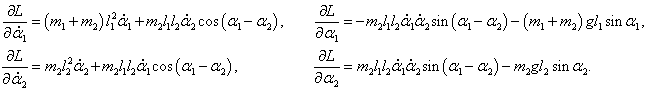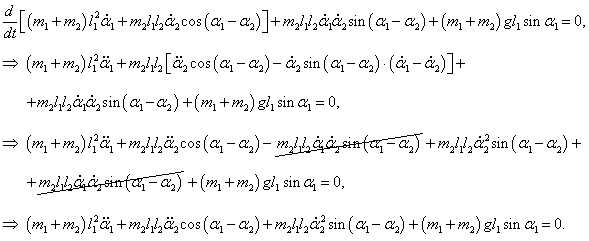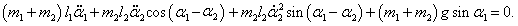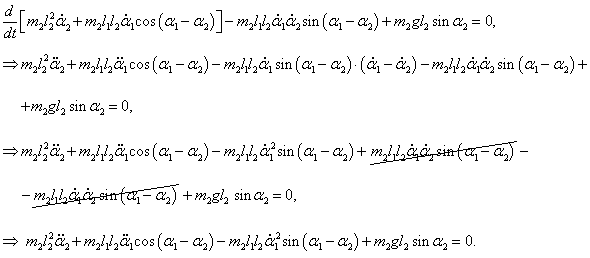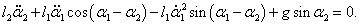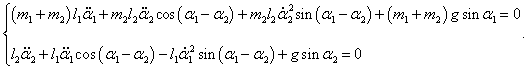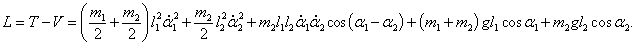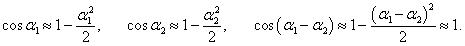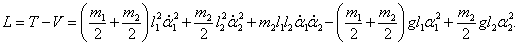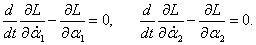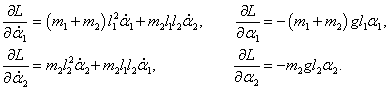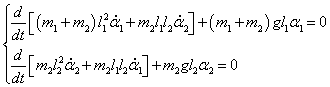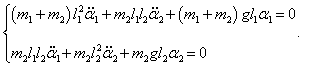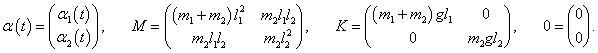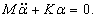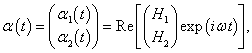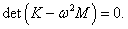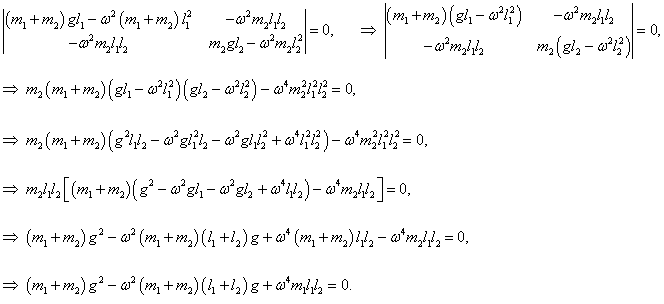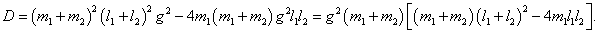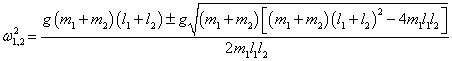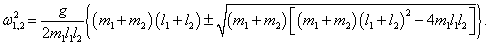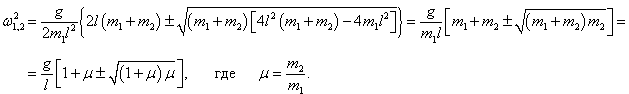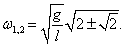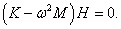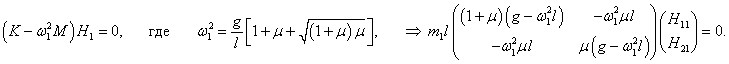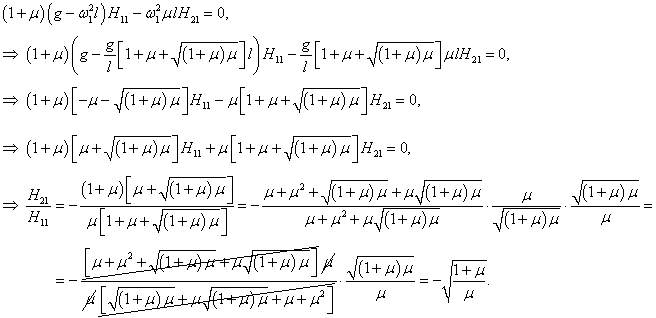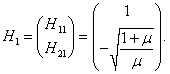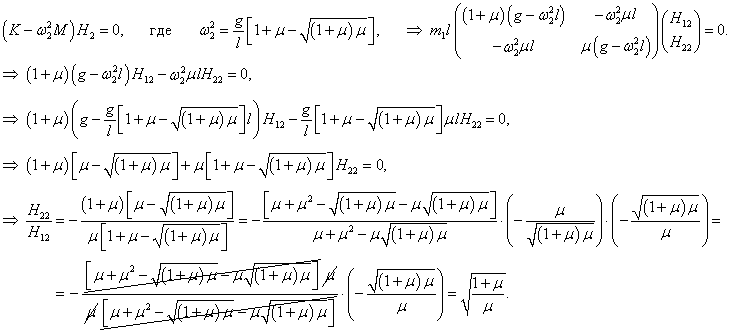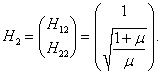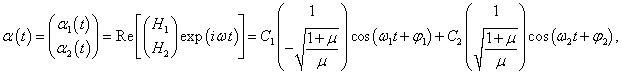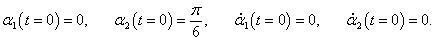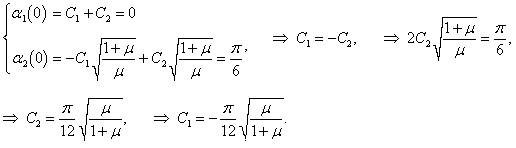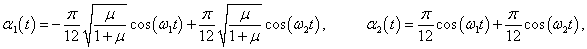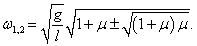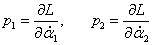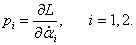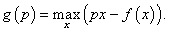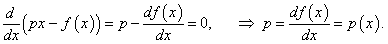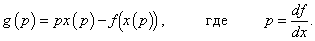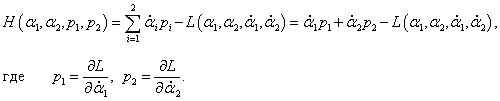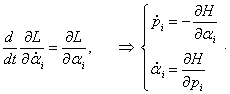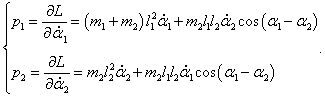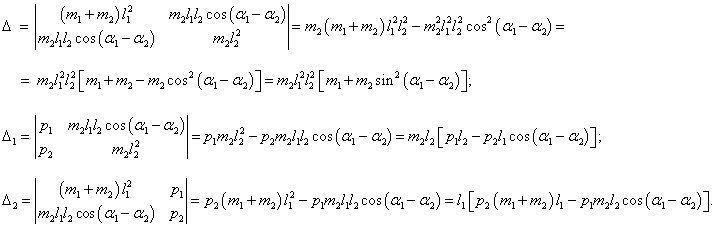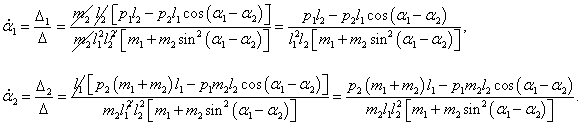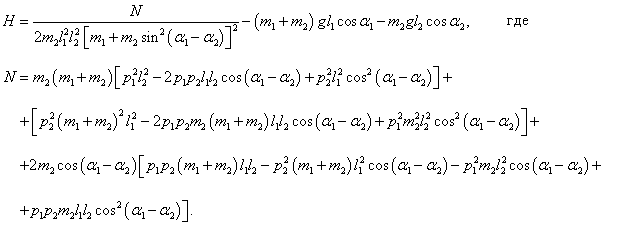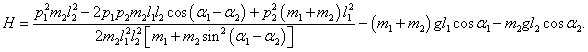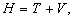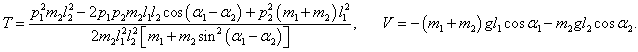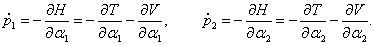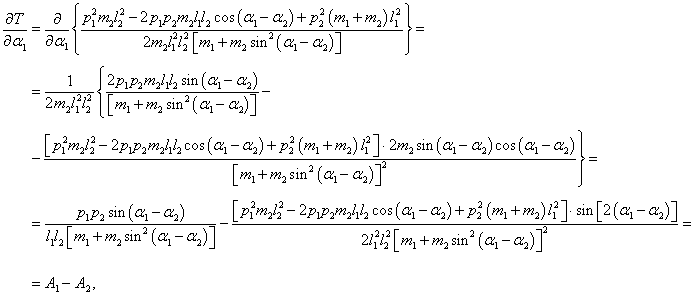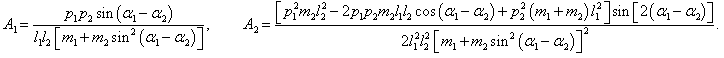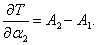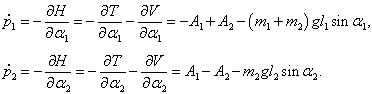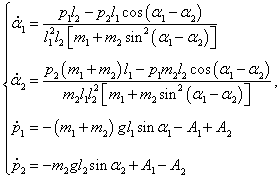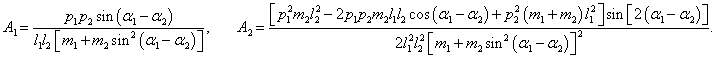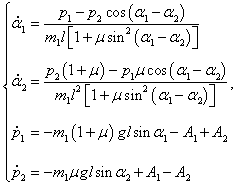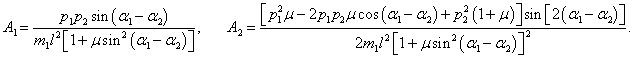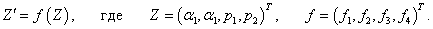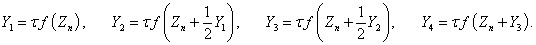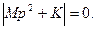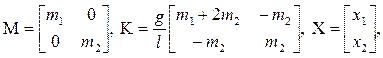Двойной маятник — это просто два маятника, соединенных один с другим. Эта система демонстрирует теорию хаоса и то, как небольшие изменения приводят к большим изменениям.
Двойной маятник — это настолько простая система, что ее может сделать пятиклассник. Но эта система и ее движение сложны и чрезвычайно интригующе.
То, как движется двойной маятник, демонстрирует хаос — идею, которая гораздо больше, чем она есть, и имеет далеко идущие последствия.
Видео:Теормех. 2021-окт-22. Группа РФЗ. Двойной маятникСкачать

Что такое двойной маятник?
Простой маятник — это масса, подвешенная к неподвижной точке. Мы видим его в маятниковых часах, которые неустанно показывают нам время. Он дает нам колебательное движение, которое легко проследить. Вы толкаете его, он колеблется туда-сюда, пока силы трения не заставят его остановиться в положении равновесия.
Двойной маятник — это именно то, на что он похож. Это простая система, состоящая из маятника, к концу которого прикреплен другой маятник.
Движение двойного маятника не так просто, как движение простого маятника.
Видео:Задача о двойном маятникеСкачать

Простой маятник против двойного маятника
Простой маятник совершает колебательное движение и приходит в состояние равновесия. Это так же точно, как восход солнца на востоке, если можно так выразиться.
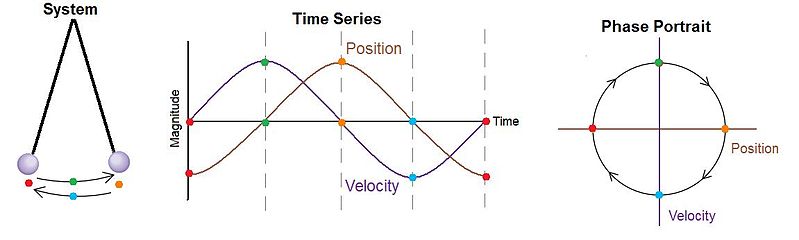
Если построить график движения маятника, его угол наклона от вертикали по оси x и скорость по оси y, то получится закручивающаяся внутрь спираль. Можно варьировать начальные условия и делать спираль меньше или больше. Но в конечном итоге спираль заканчивается в одном и том же положении. Этот график называется фазовым пространством.
Рассмотрим идеальный вариант простого маятника — точечная масса, подвешенная на безмассовом стержне. Трение и сопротивление воздуха не учитываются. Постройте график и получите петлю. Неважно, какова амплитуда маятника, это будет просто петля другого размера.
Движение простого маятника.
Не имеет значения, как вы изменяете начальные условия. Если у вас есть трение, маятник всегда будет приходить в покой в начале спирали. В противном случае она будет продолжать двигаться по замкнутой петле.
Это означает, что движение простого маятника предсказуемо. А вот двойной маятник как раз не предсказуем.
Почему двойной маятник, а не простой? Простой маятник имеет только одну степень свободы. Двойной маятник имеет две степени свободы. Для решения задач о движении двойного маятника нам нужны дифференциальные уравнения, зависящие от начальных условий. Это дает нам ингредиенты для хаоса.
Видео:Теормех. 2021-окт-18. Группа ПМФ. Двойной маятникСкачать

Движение двойного маятника
Траектория движения двойного маятника выглядит безумно и является в некотором роде беспорядочной. Для малых углов двойной маятник также дает нам простое гармоническое движение. Но при больших смещениях все обстоит иначе. Вы даже можете попробовать симуляцию живого маятника здесь .
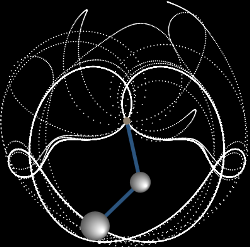
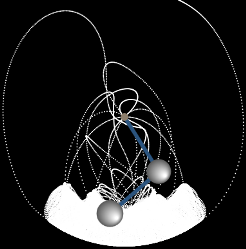
Фотография двойного маятника с длительной экспозицией с источником света показывает движение, которому он подвергается.
Мы можем описать движение двойного маятника с помощью системы обыкновенных дифференциальных уравнений. Мы обращаемся к лагранжевой механике, чтобы выяснить уравнения движения двойных маятников.
Это может показаться непонятным. Если у нас есть уравнения движения, почему система должна быть непредсказуемой? Решив уравнения, мы получим возможность предсказать движение маятника, верно?
Но проблема в том, что система двойного маятника чрезвычайно зависима от начальных условий. Если мы не можем определить начальные условия со 100% уверенностью (а в физике мы не разбрасываемся процентами), мы не можем предсказать поведение системы.
Поскольку невозможно достичь такого уровня уверенности, мы не можем предсказать движение двойного маятника. Два двойных маятника, выпущенные из одной и той же точки одновременно, будут иметь незначительные различия в начальных условиях. Это приведет к резкому изменению траектории за очень короткое время. Разница в их траекториях будет расти быстро и экспоненциально.
Сложность двойного маятника по сравнению с одинарным также напоминает пресловутую проблему трех тел. Вы можете предсказать поведение двух тел, которые влияют друг на друга. Но добавьте еще одно, и система станет слишком сложной.
Видео:Лагранжева механика. Двойной матемаческий маятник.Скачать

Двойной маятник и теория хаоса
Двойной маятник — одна из самых простых демонстраций теории хаоса. Одной из определяющих характеристик хаоса является чувствительность к изменению начальных условий.
В приведенном ниже видеоролике автор создал симуляцию 500 двойных маятников с небольшими различиями в начальных углах. Под незначительными мы подразумеваем миллионные доли радиана. Два соседних двойных маятника изначально отличаются только на одну миллионную долю радиана. Они начинают двигаться по одинаковым траекториям. Но, как вы можете видеть, через несколько секунд их пути резко расходятся.
Это происходит из-за хаотической природы системы.
Здесь следует отметить, что эта система хаотична, но не случайна. Она просто очень, очень чувствительна к начальным условиям. Если у вас есть два двойных маятника с совершенно одинаковыми начальными условиями, они пройдут один и тот же путь. Система просто очень неумолима даже к крошечным изменениям.
Но в действительности невозможно выпустить два двойных маятника с одинаковыми начальными условиями. И, следовательно, невозможно предсказать путь, который проделает маятник.
Это взгляд на то, как работают все хаотические системы. Двойной маятник демонстрирует, как мы не можем делать точные предсказания относительно хаотических систем.
Когда множество примеров собраны вместе, хаотические системы, такие как двойной маятник, образуют узоры — фракталы.
Видео:Уравнения Лагранжа второго родаСкачать

Непредсказуемость мира
Мы видим, как хаотическое поведение делает такую простую систему, как два шарика на двух нитях, практически непредсказуемой. Какие узоры могли бы образовать миллион двойных маятников, выпущенных вместе? А тройные маятники?
Наш мир состоит из множества таких хаотических систем. Даже наша Солнечная система демонстрирует хаотическое поведение, если рассматривать более длительные периоды времени. На примере двойного маятника мы видим теорию хаоса и то, как трудно предсказать окружающий нас мир.
Видео:Теормех. 2021-окт-15. Группа РФЗ. Уравнения Лагранжа.Скачать

Новое в блогах
Видео:Уравнения Лагранжа второго рода. Задача 1Скачать

Приложения пользователя
Двойной маятник — это, несомненно, настоящее чудо природы. Поразителен скачок сложности, который наблюдается при переходе от простого одиночного маятника к двойному. Колебания простого маятника имеют регулярный характер. При малых отклонениях от равновесия такие колебания являются гармоническими и описываются функцией синус или косинус. В случае нелинейных колебаний период зависит от амплитуды, но регулярность движения сохраняется. Другими словами, в случае простого маятника приближение малых колебаний вполне отражает существенные свойства системы.
Двойной маятник «ведет себя» совершенно иначе. Уже в режиме малых колебаний у двойного маятника возникает такое новое явление как эффект биений . А при увеличении энергии характер колебаний маятников меняется принципиально − колебания становятся хаотическими . Несмотря на то, что двойной маятник можно описать системой нескольких обыкновенных дифференциальных уравнений, то есть вполне детерминированной моделью, появление хаоса выглядит очень необычно. Данная ситуация напоминает систему Лоренца , где детерминированная модель из трех уравнений также демонстрирует хаотическое поведение. Попробуйте поэкспериментировать с приведенным ниже приложением и понаблюдайте за движением двойного маятника при различных отношениях масс тел и начальных углах.
Далее мы займемся построением математической модели двойного маятника в виде системы нелинейных дифференциальных уравнений. Начнем с вывода уравнений Лагранжа .
В лагранжевой механике для описания системы используются обобщенные координаты и обобщенные скорости . В нашем случае в качестве таких переменных можно взять углы отклонения маятников α1 , α2 и угловые скорости 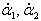
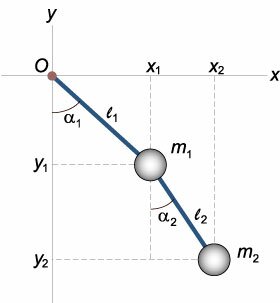
Упрощенная модель двойного маятника показана на рисунке 1. Будем считать стержни невесомыми. Их длины равны l1 и l2 . Массы точечных тел (они представлены шарами конечного радиуса) составляют m1 и m2 . В точках подвеса трение отсутствует.
Введем систему координат O xy , начало которой совпадает с точкой подвеса. Координаты маятников определяются следующими соотношениями:
Кинетическая и потенциальная энергия маятников (соответственно T и V ) выражаются формулами
Тогда лагранжиан записывается в виде
В результате лагранжиан системы принимает такой вид:
Теперь мы можем составить уравнения Лагранжа (иногда их называют уравнениями Эйлера-Лагранжа ):
Входящие в уравнения частные производные выражаются следующими формулами:
Следовательно, первое уравнение Лагранжа записывается как
Сокращая на l1 ≠ 0 , получаем:
Аналогично выведем второе дифференциальное уравнение:
После сокращения на m2l1 ≠ 0 уравнение принимает такой вид:
Таким образом, нелинейная система двух дифференциальных уравнений Лагранжа записывается как
Если считать углы α1(t) , α2(t) малыми, то колебания маятников вблизи нулевого положения равновесия можно описать линейной системой уравнений. Чтобы получить такую систему, вернемся назад к исходному лагранжиану системы:
Запишем этот лагранжиан в более простом виде, раскладывая его в ряд Маклорена и сохраняя линейные и квадратичные члены. Тригонометрические функции можно заменить следующими приближенными выражениями:
Здесь мы учли, что слагаемое с cos(α1 − α2) содержит произведение малых величин 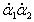
Подставляя это в исходный лагранжиан и учитывая, что потенциальная энергия определяется с точностью до константы, получаем квадратичный лагранжиан двойного маятника в виде:
Выведем дифференциальные уравнения Лагранжа для данного лагранжиана. Они записываются в таком виде:
Найдем частные производные:
Получаем систему двух дифференциальных уравнений Лагранжа:
Данную систему уравнений можно записать в компактной матричной форме. Введем матрицы
Тогда система дифференциальных уравнений представляется в виде
В случае одного тела такое уравнение описывает свободные незатухающие колебания с определенной частотой. В случае двойного маятника решение (как вы увидим ниже) будет содержать колебания с двумя характерными частотами, которые называются нормальными модами . Нормальные моды представляют собой действительную часть комплекснозначной векторной функции
где H1 , H2 − собственные векторы, ω − действительная частота. Значения нормальных частот ω1, 2 определяются из решения характеристического уравнения
Выведем общие формулы для циклических частот ω1, 2 в случае произвольных масс m1 , m2 и длин l1 , l2 :
Мы получили биквадратное уравнение для частот ω . Вычислим дискриминант:
Таким образом, квадраты нормальных частот ω1, 2 равны
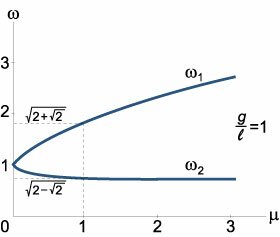
Данное выражение является несколько громоздким. Поэтому далее рассмотрим случай, когда длины стержней обоих маятников равны: l1 = l2 = l . Тогда нормальные частоты будут определяться более компактной формулой
Как видно, собственные частоты ω1, 2 зависят лишь от отношения масс μ = m2/m1 . Зависимости частот ω1 , ω2 от параметра μ (при условии g/l = 1 ) показаны выше на рисунке 2. В частности, при равных массах m1 = m2 = m , т.е. при μ = 1 , собственные частоты равны
Теперь, после того как собственные частоты ω1, 2 известны, для описания нормальных мод нужно определить еще собственные векторы H1, 2 . Они находятся из решения векторно-матричного уравнения
Пусть собственный вектор H1 = (H11, H21) T (верхний индекс T означает операцию транспонирования) соответствует нормальной частоте ω1 . Тогда получаем следующее уравнение для определения H1 :
Координаты собственного вектора H1 удовлетворяют уравнению
Таким образом, собственный вектор H1 равен
Аналогичным образом найдем координаты второго собственного вектора H2 = (H12, H22) T :
Следовательно, собственный вектор H2 имеет такие координаты:
Общее решение матричного уравнения записывается в виде
где постоянные C1 , C2 , φ1 , φ2 зависят от начальных положений и скоростей маятников.
Рассмотрим характер малых колебаний для некоторого конкретного набора начальных данных. Пусть, например, координаты и скорости маятников в начальный момент имеют такие значения:
В этом случае начальные фазы равны нулю: φ1 = φ2 = 0 . Определим постоянные C1 и C2 :
Тогда закон колебаний маятников выражается формулами
где циклические частоты ω1, 2 определяются соотношением
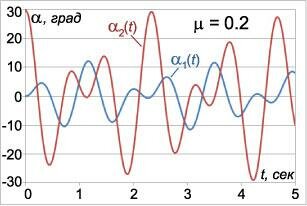
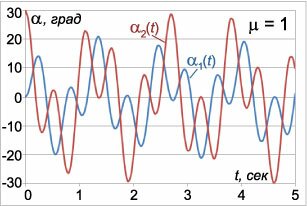
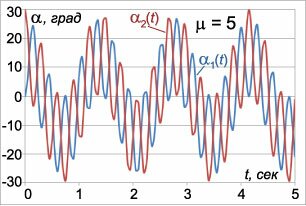
Здесь углы α1(t) , α2(t) выражаются в радианах, а время t в секундах. На рисунках 3-5 приведены графики малых колебаний маятников для трех значений μ : μ1 = 0.2 , μ2 = 1 , μ3 = 5 , при условии l = l1 = l2 = 0.25 м , g = 9.8 м/c 2 . Углы отклонения маятников для удобства приведены в градусах. Из графиков видно, что в системе происходят биения , при которых энергия циклически переходит от одного маятника к другому. Когда один маятник почти останавливается, другой раскачивается с максимальной амплитудой. Через некоторое время маятники «меняются ролями» и так далее. Колебания с большей частотой ω1 модулируются более низкочастотными колебаниями с частотой ω2 . Это особенно хорошо заметно на рисунке 5 при большом значении μ ( μ3 = 5 ), когда разница между частотами ω1 и ω2 велика.
Итак, малые колебания двойного маятника имеют периодический характер и описываются суммой двух гармоник с частотами ω1 , ω2 , зависящими от параметров системы. Характерным свойством малых колебаний двойного маятника является эффект биений .
Вернемся теперь снова к исходной нелинейной системе уравнений и исследуем характер колебаний с произвольной амплитудой. Такая система уравнений не решается аналитически. Поэтому мы будем рассматривать численную модель двойного маятника.
Приведенные выше уравнения Лагранжа являются дифференциальными уравнениями второго порядка. Их удобнее преобразовать в форму канонических уравнений Гамильтона . В результате вместо 2 уравнений второго порядка мы получим систему 4 дифференциальных уравнений первого порядка.
В гамильтоновой механике состояние системы определяется обобщенными координатами и обобщенными импульсами . В нашем случае в качестве обобщенных координат мы снова, как и в уравнениях Лагранжа, будем использовать углы α1 , α2 . Вместо обобщенных скоростей 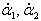
или в краткой записи:
Переход от лагранжевой к гамильтоновой форме уравнений производится с помощью преобразования Лежандра , которое определяется следующим образом.
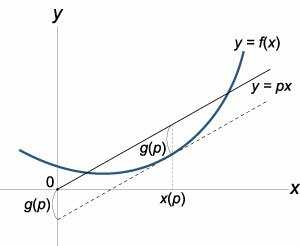
Предположим, что f ( x ) − гладкая выпуклая вниз функция (рисунок 6). Рассмотрим прямую y = px , проходящую через начало координат. Расстояние между прямой y = px и функцией y = f(x) вдоль оси O y зависит от координаты x . При определенном значении x это расстояние будет максимальным. Ясно, что оно зависит от наклона прямой, т.е. от параметра p . Таким образом мы вводим новую функцию g ( p ):
Такое преобразование функции f ( x ) в сопряженную функцию g ( p ) называется преобразованием Лежандра . Заметим, что функция g ( p ) достигает максимального значения по переменной x когда p = df/dx . Действительно,
Зная зависимость p ( x ), можно найти обратную функцию x ( p ). Тогда преобразование Лежандра будет выражаться соотношением
Преобразование Лежандра легко обобщается на случай функций нескольких переменных. В модели двойного маятника переход от функции Лагранжа к функции Гамильтона описывается преобразованием Лежандра в форме:
В этом выражении L является лагранжианом, а функция H представляет собой гамильтониан системы, который зависит от обобщенных координат α1 , α2 и обобщенных импульсов p1 , p2 .
В результате такого преобразования каждое уравнение Лагранжа переходит в систему двух канонических уравнений Гамильтона, имеющих вид:
Определим теперь конкретный вид уравнений Гамильтона для двойного маятника. Обобщенные импульсы p1 , p2 выражаются через частные производные лагранжиана в виде
Решим эту систему уравнений и выразим угловые скорости через обобщенные координаты и импульсы. Воспользуемся формулами Крамера и вычислим соответствующие определители:
Отсюда получаем следующие выражения для угловых скоростей:
Эти формулы представляют собой первые 2 (из 4) дифференциальных уравнений Гамильтона. С учетом данных выражений гамильтониан можно записать в следующем виде:
Последнюю формулу можно представить как
Числитель N в этом выражении является весьма громоздким. Упростим его:
Следовательно, функция Гамильтона принимает такой вид:
Здесь первое слагаемое представляет собой обобщенную кинетическую энергию T , а два других слагаемых − потенциальную энергию V , т.е. гамильтониан H определяется как
Теперь мы можем составить еще два дифференциальных уравнения Гамильтона для обобщенных импульсов:
Вычислим отдельно частные производные обобщенной кинетической энергии:
где символами A1 и A2 обозначены выражения
Производная кинетической энергии T по переменной α2 будет иметь такой же вид, только с противоположным знаком:
Отсюда получаем уравнения Гамильтона в виде:
Итак, в результате громоздких преобразований мы получили то, к чему так долго стремились − систему 4 канонических уравнений Гамильтона, описывающих движение двойного маятника. Запишем их вместе в окончательном виде:
Теперь можно приступить к численному анализу уравнений.
Наиболее распространенным методом численного решения дифференциальных уравнений является метод Рунге-Кутты 4-го или 5-го порядка точности. Различные вариации этого метода используются в большинстве математических пакетов (MatLab, Maple, Mathematica, Mathcad), как правило, с автоматическим контролем точности и адаптивным временным шагом.
Для моделирования движения двойного маятника мы также воспользуемся классическим методом Рунге-Кутты 4-го порядка точности. Предварительно несколько упростим дифференциальные уравнения, полагая, что длины маятников одинаковы: l1 = l2 = l . Введем также параметр μ , равный отношению массы второго маятника к массе первого: μ = m2/m1 . Тогда система уравнений принимает следующий вид:
Данную систему можно переписать в векторной форме:
Вектор Z составлен из 4-х канонических переменных данной системы, а компоненты вектора f соответствуют правым частям дифференциальных уравнений.
Метод Рунге-Кутты предполагает на каждом шаге последовательное вычисление четырех промежуточных векторов:
Значение вектора Zn+1 в следующем временном узле вычисляется по формуле
Суммарная ошибка данного алгоритма на конечном интервале имеет порядок O(τ 4 ) , т.е. точность вычислений возрастает в 16 раз при уменьшении временного шага τ в два раза.
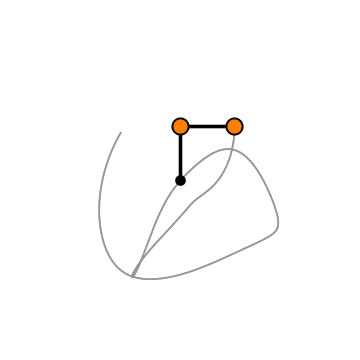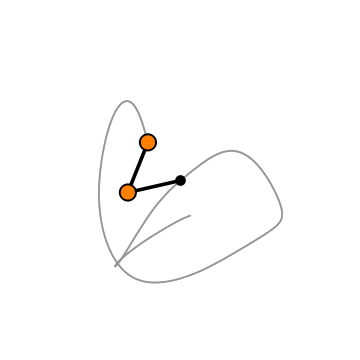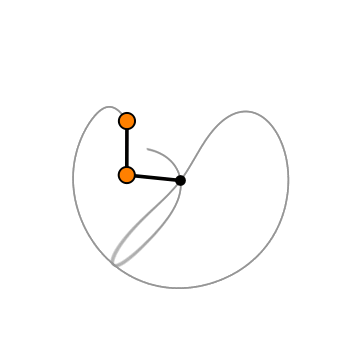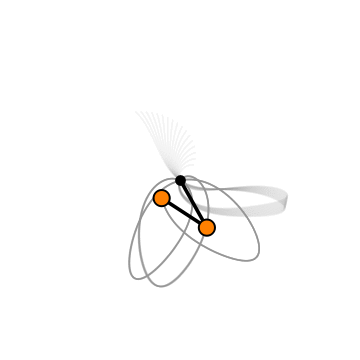
Описанная модель реализована в анимации, приведенной в начале web-страницы. Для упрощения мы положили начальные углы отклонения маятников равными: α1 = α2 = α . Данное приложение наглядно демонстрирует хаотическую динамику двойного маятника при различных значениях параметров μ и α . Интересно, что в некоторых режимах в системе возникают устойчивые траектории, как, например, на рисунке 7 , или компактные области притяжения, как на рисунке 8. Похоже, что двойной маятник еще не полностью изучен физиками и математиками и таит в себе много неожиданностей.

И обратная задача — даны уравнения движения, найти М1(t), M2(t)

===
Представьте кульман с чертежным пантографом. Ведь каждой точке на доске соответствует строго определенное положение системы рычагов. Вот посмотрите на картинку, на мой взгляд тут есть взаимно-однозначное соответствие между динамическим уравнением происходящего на узлах и кинематическим уравнение движения карандаша.

Мне хотя бы название области механики где про это почитать. Имеется ввиду манипулятор. Ну как «рука» у робота, и какие силы в узлах прикладывать чтобы она двигалась в нужном направлении.
В трех измерениях конечно будет неоднозначность, а на плоскости по-моему нет.
Видео:Т. Уравнения Лагранжа 2 рода. Теория.Скачать

МОДЕЛИРОВАНИЕ ДВОЙНОГО МАЯТНИКА
Дата добавления: 2015-06-12 ; просмотров: 6267 ; Нарушение авторских прав
Цель работы: исследование колебаний двойного маятника путем компьютерного моделирования в пакетах SIMULINK и MATLAB.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Вывод дифференциальных уравнений двойного маятника.
Динамика механических систем описывается законами Ньютона. При отсутствии трения они приводят к системе линейных дифференциальных уравнений второго порядка, матричная запись которых имеет вид

где М, K – постоянные матрицы размеров m ´ m.
Если, например, речь идет о движении системы материальных тел, то векторы Х и 
Для консервативных колебательных систем (систем без трения и потерь энергии) корни получаются чисто мнимыми pi= ±jω1. Положительные числа w1, . wm называются циклическими частотами системы.
Таким корням соответствует общее решение вида
где сi, ji – произвольные постоянные. Векторы Hi удовлетворяют алгебраическим уравнениям вида 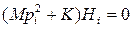
В качестве примера механической системы, описываемой уравнениями вида (1), рассмотрим двойной маятник. Так называют систему из двух маятников – тяжелого, массы m1 и легкого, массы m2. Легкий маятник подвешен к тяжелому, как это показано на рис. 1. Массы m1 и m2 будем считать точечными, длины нитей – одинаковыми l1 = l2= l, углы a1 и a2 – малыми.
При указанных условиях для двойного маятника характерно так называемое явление биений, сопровождаемое циклическим обменом энергией между маятниками. Внешне картина колебаний выглядит довольно неожиданно: без видимых причин один из маятников время от времени самопроизвольно останавливается, а другой начинает интенсивно раскачиваться. Подобные колебания могут возникать при спуске на парашюте, при подъеме по веревочной лестнице и в других ситуациях.
Для вывода дифференциальных уравнений малых колебаний двойного маятника воспользуемся законом сохранения полной энергии Е, согласно которому
| Рис 1. Двойной маятник |
где ЕK и ЕП – кинетическая и потенциальная энергии.
Выражение для кинетической энергии малых колебаний имеет вид

где х1 и х2 – горизонтальные отклонения тяжелого и легкого маятников от положения равновесия. Потенциальная энергия определяется вертикальным отклонением маятников h1 и h2:

Подставляя выражения (4) и (5) в (3) и переходя к матричной форме записи, получаем

знак Т означает транспонирование.
Геометрически уравнение (6) задает некоторый эллипсоид в четырехмерном пространстве состояний с координатами 
Чтобы найти уравнение такой траектории, продифференцируем равенство (6) по времени:

При дифференцировании мы воспользовались следующей формулой:
Равенство (7) должно выполняться при любых значениях первого сомножителя, поэтому второй сомножитель должен равняться нулю
Мы нашли систему дифференциальных уравнений, описывающих движение двойного маятника. Ее более подробная запись имеет вид

Переходя к скалярным уравнениям и вводя обозначения m 2 =m2/m1, k 2 = g/l, окончательно получаем
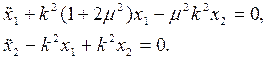
1.2. Решение дифференциальных уравнений двойного маятника.
Уравнения (8) можно решить аналитически, так как они представляют собой линейные однородные дифференциальные уравнения с постоянными коэффициентами. Для упрощения дальнейших выкладок положим k = 1 и будем считать m
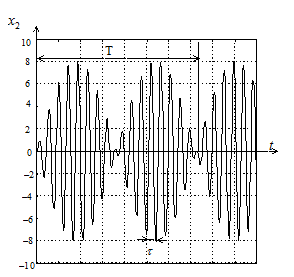
Рис. 2. Графики колебаний двойного маятника
Графики представляют собой «быстрые» колебания с периодом 2p, модулированные «медленными колебаниями» с периодом 2pm, и наглядно описывают явление биений, заключающееся в циклической «перекачке» энергии от одного маятника к другому.
Биения можно охарактеризовать тремя параметрами – периодом быстрых колебаний t, периодом медленных колебаний Т и числом «быстрых» колебаний за период биений
n = T/t.
 |
Построение графика фазовой траектории также удобно начинать с нахождения его «огибающей», т.е. геометрической фигуры, внутри которой он расположен. Для двойного маятника такой фигурой является ромб с центром в начале координат.
| Рис. 3. Траектория в плоскости x1, x2 |
Чтобы построить фазовую траекторию, следует сначала нарисовать этот ромб, а затем, пользуясь полученными ранее таблицей и графиками рис. 2, последовательно наносить точки (х1, х2), соответствующие экстремумам и нулям функций х1 и х2 , и соединять их плавной кривой, вписанной в ромб. Если отказаться от упрощающего предположения m 2 =1+2µ 2 ), соединенных в «кольцо». Левая схема моделирует колебания легкого маятника, правая – тяжелого, взаимное влияние маятников учитывается связями между схемами (коэффициенты k 2 и m 2 k 2 ). Начальные условия, показанные на схеме, означают, что в первый момент тяжелый маятник отклоняют от положения равновесия и без толчка отпускают, легкий маятник при этом имеет нулевые значения скорости и координаты.
Используя схему рис. 4, легко получить матрицы описания двойного маятника в пространстве состояний:
Введение вектора B = [0 0 0 1] T позволяет рассматривать движение двойного маятника при наличии управляющего воздействия, приложенного к нижнему маятнику.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
В лабораторной работе осуществляется компьютерное моделирование двойного маятника в пакетах SIMULINK и MATLAB. Основой для моделирования является схема рис. 4 и описание в пространстве состояний. Численные значения параметров двойного маятника приведены в таблице вариантов.
Отчет должен содержать:
1. Теоретическое решение системы уравнений (8) при заданных значениях k, m 2 для начальных условий х1(0) = 5;
2. Расчет численных значений параметров Т, t, n, таблицу и графики функций х1(t), х2(t), график фазовой траектории х2 = f(х1); графики должны отражать полтора – два периода биений.
3. Матрицы A, b, c описания системы в пространстве состояний в случае приложения управляющего воздействия к нижнему маятнику и передаточную функцию системы для этого случая.
4. Схему моделирования исходной системы в SIMULINK и программу моделирования на языке MATLAB.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Выполнить в пакете SIMULINK раздельное моделирование колебательных звеньев (маятников) (рис. 4), не соединяя их между собой. Принимая n = 1, установить нулевые начальные условия. Подать на входы обеих звеньев единичный входной сигнал и убедиться, что колебания на выходах звеньев совпадают (полупериод колебаний должен равняться t = p/k).
2. Отключить единичный сигнал, соединить звенья между собой «в кольцо», согласно рис. 4, установить начальные условия х1(0) = 1. Наблюдать графики сигналов х1(t), х2(t) и их разности. Сравнить экспериментальные оценки величин Т, t, n с их теоретическими значениями.
3. Выполнить моделирование двойного маятника в пакете MATLAB, используя описание в пространстве состояний и приняв n = m. Наблюдать фазовую траекторию х2 = f(х1) (на экране должен быть виден ромб).
4. Установить коэффициент n 2 = 1+2m 2 , наблюдать изменения фазового портрета («перекос» ромба).
5. Найти начальные условия, при которых оба маятника качаются синхронно (синфазно и противофазно). Исследовать поведение двойного маятника в случае приложения управляющего воздействия к нижнему маятнику.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. 
Рис. 5. Двухмассовая система с
 |
Требуется, используя закон сохранения энергии, найти дифференциальное уравнение малых колебаний, определить циклические частоты и составить схему моделирования. Принять m1= m2=1, k =1, трением пренебречь. Для определения потенциальной энергии сжатой пружины использовать формулу ЕП = kx 2 .
2. Две массы, соединенные пружиной, лежат на полированном столе (рис. 6). Их прижимают друг к другу и отпускают. Составить дифференциальное уравнение и исследовать движение такой системы, полагая m1= m2 = m, k = 1.
Рис. 6. Двухмассовая система со свободными концами
3. Какой вид примет теоретическое решение (10) в случае n 2 ¹ 1?
4. Найти вид теоретического решения и график фазового портрета уравнений (9) при следующих значениях начальных условий:
а) 

5. Какие условия надо выполнить, чтобы обеспечить колебания двойного маятника с первой циклической частотой? Со второй циклической частотой?
6. При соединении схем моделирования, показанных на рис.4, между ними по ошибке включили инвертор. Найти вид сигнала x1 в этом случае, если m = 0,1, k = 1, n = 1.
7. Вывести уравнения (8) с помощью второго закона Ньютона.
5. ВАРИАНТЫ ЗАДАНИЙ
| № | |||||||||||
| k, c -1 | |||||||||||
| 100m 2 | 0,5 | 1,5 | 2,0 | 1,0 | 0,5 | 2,0 | 1,5 | 2,0 | 3,5 | 2,5 | 0,5 |
| № | |||||||||||
| k, c -1 | |||||||||||
| 100m 2 | 1,0 | 1,5 | 0,5 | 2,0 | 1,5 | 0,5 | 4,0 | 2,0 | 3,0 | 0,5 | 1,0 |
| № | |||||||||||
| k, c -1 | |||||||||||
| 100m 2 | 2,5 | 1,0 | 3,0 | 2,5 | 1,5 | 0,5 | 3,0 | 1,0 | 1,5 | 3,0 | 0,5 |
Лабораторная работа № 5
МОДЕЛИРОВАНИЕ КОЛЕБАНИЙ СТРУНЫ
Цель работы:ознакомиться с методикой компьютерного моделирования колебаний струны с помощью пакетов MATLAB и SIMULINK.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.2. Собственные частоты и собственные колебания струны.
Задача о поперечных колебаниях струны– одна из классических задач математической физики. В ней рассматривается туго натянутая струна, закрепленная в конечных точках. Если вывести струну из положения равновесия, например, оттянуть ее и затем отпустить, то струна начнет колебаться. В процессе колебания величина отклонения u будет зависеть от абсциссы точки струны х и времени t. Таким образом, чтобы знать положение любой точки струны в произвольный момент времени, надо найти зависимость u от х и t, т.е. найти функцию u(x,t). Если считать струну абсолютно гибкой, упругой (подчиняющейся закону Гука) и рассматривать малые колебания, то функция u(x,t) удовлетворяет уравнению:


где Т – сила натяжения струны, r – ее линейная плотность (масса единицы ее длины).
Уравнение (1) называется уравнением свободных колебаний струны или одномерным волновым уравнением. К нему сводится не только рассматриваемая задача, но и многие другие, например, задача о поперечных колебаниях летательных аппаратов, задача о флаттере (колебаниях крыла самолета).
Для выделения конкретного решения в задаче о колебании струны задаются граничные условия двух видов: начальные и краевые. Начальные условия показывают, в каком состоянии находилась струна в момент начала колебания (т.е. описывают форму струны и скорость ее точек при t = 0). Начальное состояние струны задается двумя функциями:

Краевые условия показывают, что происходит на концах струны во время колебаний. Если концы струны закреплены (начало струны – в начале координат, а конец – в точке х=l), функция u(x,t) будет подчиняться условиям:

Характер колебаний струны сильно зависит от начальных условий. Наиболее простой случай получается, когда в начальный момент времени струне придают форму полуволны синусоиды f(x)=sinπx / l и отпускают без начальной скорости. Тогда все точки струны будут совершать гармонические колебания с одной и той же частотой ω1, так что в любой момент времени форма струны будет отличаться от исходной только амплитудой (рис. 1,а).
Рис. 1. Первое и второе собственные колебания струны
Математически такие колебания описываются формулой

Это так называемое первое собственное колебание струны, ему соответствует низкочастотный чистый тон. Именно он используется музыкантами при настройке гитары или рояля. Чтобы найти первую собственную частоту ω1, подставим функцию (4) в уравнение (1). После дифференцирования и сокращения на общий множитель получаем:
Таким образом, решение уравнения (1) в рассматриваемом случае описывается формулой

Второе собственное колебание получим, задав начальное условие в виде f(x)=sin2πx/l. Форма струны в различные моменты времени для этого случая показана на рис. 1,б. Она описывается уравнением
Подставляя эти выражения в уравнение (1), находим, что вторая собственная частота ω2=2aπ/l. Отсюда получаем формулу для второго собственного колебания

Аналогично выводятся формулы для третьего и остальных собственных колебаний:
Если струна колеблется с собственной частотой ωk=kaπ/l, то у нее будут k+1 неподвижных точек (узлов) и k точек пучности (точек, где отклонения достигают максимума). Колебания такого вида называются стоячими волнами.
Когда струна колеблется, она издает звук, высота которого возрастает с частотой колебаний. Если струна совершает собственные колебания, то самый низкий тон будет, когда частота равна w1. Остальные тона, соответствующие частотам wk, называются обертонами или гармониками. Если струна совершает свободные колебания, то функция u(x, t), представляется в виде суммы отдельных гармоник. Это позволяет записать общее решение уравнения (1) в виде бесконечного ряда Фурье.
1.2. Дискретизация пространственной координаты.
Для перехода от уравнения (1) к конечномерной модели осуществим дискретизацию задачи по переменной x. В результате получится система обыкновенных дифференциальных уравнений, число уравнений в ней зависит от шага дискретизации h. С этой целью выделим на струне n равноотстоящих точек с координатами х1, х2, . хn (рис. 2).
 |
Тем самым струна условно разбивается на n равных участков длины h = l/n и заменяется приближенной моделью в виде n–1 масс (точек, бусинок), закрепленных на невесомой нити. Движение рассматриваемых точек в процессе колебаний струны будет описываться некоторыми функциями времени u1(t), u2(t), . un-1(t). Для вычисления второй производной по х от функции и воспользуемся приближенной формулой
Записывая теперь уравнение (1) для точек x1, x2, . xn–1, получаем систему обыкновенных дифференциальных уравнений второго порядка

с граничными условиями u0 = 0, un = 0, ui(0) = f(xi). Она представляет собой конечномерную модель струны.
В частности, для n = 4, b =1 эта модель будет содержать три уравнения

Суммарный порядок уравнений равен 6, т.е. мы имеем дело с шестимерной моделью.
Начальную скорость струны будем считать нулевой 

Решение будем искать в виде U=Hcosωt, где вектор Н и частота ω подлежат определению. После подстановки этого выражения в (9) получаем соотношение
Это означает, что Н и -ω 2 – собственные векторы и собственные числа матрицы А0. Чтобы найти собственные числа, выписываем характеристический полином матрицы А0:
и находим его корни
Им соответствуют собственные векторы, удовлетворяющие алгебраическим уравнениям A0Hi=liHi:
и собственные частоты 

Уравнения для их определения получаем из соотношения (10) при t=0:
В нашем случае получаем систему
Она легко решается:
Этим завершается получение аналитического решения для дискретной модели струны (8).
Особенно простые решения получаются, когда начальная форма струны симметрична относительно середины u1(0)= u3(0), при этом свойство симметрии сохраняется и в процессе колебаний. Например, при u1(0)= u3(0)=2, u2(0)=0 получим
1.3. Моделирование в SIMULINK.
|
Для структурного моделирования системы уравнений (8) воспользуемся методом Кельвина, применяя его к каждому из трех уравнений по отдельности и затем соединяя полученные схемы между собой. В результате получаем схему моделирования на сумматорах и интеграторах, показанную на рис. 3. В его нижней части условно изображена исследуемая струна, разбитая на 4 участка. Схема содержит три фрагмента, соединенных прямыми и обратными связями. Выход первого фрагмента u1 характеризует колебания точки струны х1, выход второго фрагмента u2 характеризует колебания точки х2 и т.д.
Выходы внутренних интеграторов каждого из трех фрагментов показывают, как изменяются скорости тех же точек.
При реализации схемы в SIMULINK нужно на входах интеграторов И1, И3, И5 поставить сумматоры, а выходные сигналы интеграторов И2, И4, И6 наблюдать с помощью блока осциллографа Scope. Перед началом моделирования на интеграторах И2, И4, И6 устанавливаются начальные условия, соответствующие начальной форме струны, а на интеграторах И1, И3, И5 – условия, соответствующие начальным скоростям точек х1, х2, х3 (в нашем случае они равны нулю).
1.4. Моделирование в MATLAB.
Для численного моделирования уравнений (8) в MATLAB удобнее всего использовать команду initial. Предварительно надо ввести матрицы A,B,C,D описания в пространстве состояний и сформировать структуру sys=ss(A,B,C,D). В нашем случае эти матрицы имеют вид
Они могут быть получены из системы (8) после введения переменных u4, u5, u6, равных скоростям точек х1, х2, х3, либо по схеме рис. 3 путем выписывания уравнений для каждого интегратора.
Далее вводится массив времени t и вектор начальных условий U0 (его первые три компоненты – заданные числа, следующие три – нули). При формировании матриц в MATLAB можно пользоваться командами zeros, eye, ones, например:
Результат выполнения команды
можно наблюдать с помощью команд plot(t, U)– обычные графики, и mesh (U) – графики поверхности u(x, t) в трехмерном пространстве.
В MATLAB можно получить не только численное, но и символьное решение системы дифференциальных уравнений (8). Это делается с помощью команды dsolve тулбокса SYMBOLIC. Входными аргументами команды служат дифференциальные уравнения и начальные условия (те и другие заключаются в одиночные кавычки – строковый формат).
В нашем случае набираем код
Результатом выполнения первой команды будет символьная структура. Второй командой извлекаем из нее переменные u1, u2, u3 и упрощаем их. Полученные формулы с точностью до обозначений совпадают с решением, найденным ранее в п. 1.2.
Для визуализации символьных решений служат команды ezplotи ezsurf. В качестве примера их использования на рис. 4 показаны поверхности, отвечающие первому и второму собственным колебаниям струны, описываемым формулами (5), (6)..
|
Они построены с помощью команд
Рис. 5 иллюстрирует погрешность, вносимую дискретизацией пространственной координаты.
Рис. 5. Графики собственного колебания для непрерывной и дискретной моделей
На нем показаны графики второго собственного колебания, полученные путем решения уравнения в частных производных (1) и системы дифференциальных уравнений (8) при 

Очевидно, что с увеличением числа участков, на которые разбивается струна при дискретизации, кривые будут сближаться.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Изобразить на графике начальную форму струны для своего варианта. Провести дискретизацию уравнения (1), условно разбив струну на четыре равных участка.
2. Решить полученную систему уравнений теоретически. Для заданной f(x) построить графики ui(t), для трех точек струны х=0,25; 0,5; 0,75.
3. Составить полную схему моделирования для SIMULINK. Рассчитать амплитуду и период косинусоиды на выходе каждого из трех фрагментов схемы при отсутствии связей между ними.
4. Рассчитать начальные условия U1(0) и U2(0) для получения первого и второго собственных колебаний шестимерной модели струны. Оценить, на сколько процентов отличаются их собственные частоты от теоретических.
5. Выписать матрицы А, В, С описания в пространстве состояний, привести программы численного и символьного моделирования в MATLAB.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Собрать в SIMULINK три фрагмента схемы моделирования, не соединяя их между собой. Проверить их идентичность, установив везде одинаковые начальные условия и сравнить выходы схем.
2. Соединить схемы между собой, установить начальные условия для получения первого и второго собственных колебаний. Сравнить их графики с теоретическими.
3. Установить начальные условия для своего варианта, полученные графики сравнить с теоретическими.
4. Выполнить моделирование в MATLAB, используя матрицы описания в пространстве состояний и команду initial. Построить график поверхности u(x, t) в трехмерном пространстве, используя команду mesh.
5. Получить символьное решение в MATLAB, используя команду dsolve. Визуализировать полученное решение с помощью команды ezsurf.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Чем определяется общее число граничных условий? Чем краевые условия отличаются от начальных? Какой вид имеют начальные условия в задаче о колебаниях струны при игре на рояле и на гитаре?
2. Вывести формулы конечно-разностной аппроксимации первой и второй производных. Оценить точность этих формул на конкретном примере.
3. Что такое собственные колебания и собственные частоты? Какой физический смысл этих понятий? Нарисуйте для различных моментов времени форму струны, колеблющейся с третьей собственной частотой.
4. Выполнить дискретизацию, разбив струну на 3 участка и приняв b=1. Для полученной системы дифференциальных уравнений: а) найти собственные частоты колебаний; б) найти собственные векторы матрицы А0; в) найти начальные условия для получения собственных колебаний; г) найти решение для случая
5. Найти решение и нарисовать графики колебаний струны для своего варианта при
6. Провести для уравнения струны дискретизацию не по пространственной переменной х, а по времени t. Сравнить полученную схему моделирования со схемой для дискретизации по пространству. Указать физический смысл начальных условий для четных и нечетных интеграторов. Какие сигналы следует подавать на вход первого и последнего фрагментов схемы?
5. ВАРИАНТЫ ЗАДАНИЙ
Рассматривается струна единичной длины (l=1) с закрепленными концами. Ее движение описывается волновым уравнением (1) с нулевыми граничными условиями (3). Начальные условия задаются формулами (2), причем


Значения коэффициентов а1, а2 и параметра b, входящего в уравнения (7), приведены в таблице.
📽️ Видео
Уравнение ЛагранжаСкачать

№1. Уравнения Лагранжа 2 рода. Задача 1.Скачать

Видеоурок по физике "Математический и пружинный маятники"Скачать

Лагранжева механика. Математический маятник.Скачать

математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Решение уравнения ЛагранжаСкачать

Лагранжева механика. Двойной физический маятник.Скачать

Математические и пружинные маятники. 11 класс.Скачать

Уравнение Лагранжа 2-го рода для механизма с одной степенью свободыСкачать

Математический маятник или откуда формула периодаСкачать

Двойной маятникСкачать

Вывод уравнения Лагранжа 2-го родаСкачать