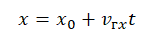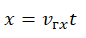Движения двух материальных точек заданы уравнениями x1 15 t (4 видео)

Движения двух материальных точек заданы уравнениями х1 = 15 +t^2 и х2 = 8 • t. Охарактеризуйте движение каждой материальной

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Решение задачи 7. Вариант 335
Уравнение координаты при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Совместное движение двух тел
📸 Видео

Видео:Решение графических задач на равномерное движениеСкачать

Ваш ответ

Видео:Задачи на движение двух объектовСкачать

решение вопроса

Видео:Движение двух велосипедистов задано уравнениями x1=2t (м) и x2=100-8t (м) - №22625Скачать

Решение задачи 7. Вариант 335

Движение двух материальных точек вдоль одной прямой заданы уравнениями ( S_=4t^2+2 ) , ( S_=3t^2+4t-1 ) ( S1, S2–пройденный путь в метрах, ‐время в секундах). Найдите скорости движения точек в те моменты, когда пройденные ими расстояния равны. В ответе укажите сумму всех полученных значений скоростей.

Найдем время, когда они прошли одинаковые расстояния, составим уравнение

( t=1 ) — скорости сравнялись в первый раз

( t=3 ) — скорости сравнялись во второй раз

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

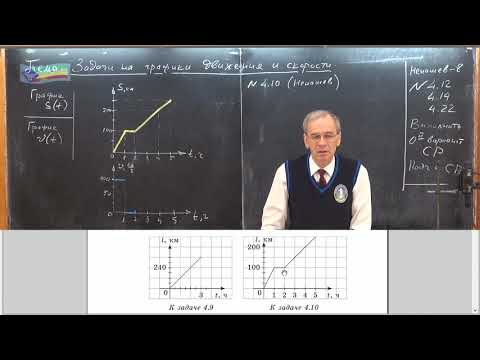
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение