Движение жидкости уравнение бернулли конспект (4 видео)

План-конспект урока по физике в 10 классе на тему : Движение в жидкостях и газах. Уравнение Бернулли.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

План-конспект урока по физике в 10 классе

Тема урока: Движение в жидкостях и газах. Уравнение Бернулли.

Добиться усвоения учащимися понимания движения жидкостей и газов, уравнения Бернулли

Продолжить воспитание отношения к физике, как к интересной и необходимой науке;

Формировать у учащихся аккуратность, при работе с записями в тетради.

Продолжить формирование умения высказывать умозаключения;

Развитие самостоятельности в суждениях;

1. Организационный момент

Приветствие, выявление отсутствующих, проверка готовности учащихся к уроку.

2. Опрос домашнего задания

Динамика вращательного движения

3.Обьяснение новой темы

Вы знаете, что в состоянии покоя жидкости и газы оказывают давление на стенки сосуда. В природе и в быту жидкость находится не только в состоянии покоя, но и в движении. Какие силы возникают в текущей по арыкам, каналам, рекам и водопроводным трубам воде?

Для изучения этого явления рассмотрим поверхность воды, текущей в арыке. В середине широкого полноводного канала вода, в основном, течет равномерно по одной линии. В этом можно удостовериться, наблюдая за телами, плывущими в воде Такое течение называется послойным или ламинарным . Вода в горной реке течет быстро. Если наблюдать за телами, плывущими по этой реке, то можно увидеть, что течение образовывает водовороты Такое течение называется турбулентным . Значит, если жидкость течет по трубам, то за счет трения о стенки трубы слои жидкости текут с разной скоростью: в середине т р у б ы – быстрее, у с т е но к – медленнее. Рассмотрим течение жидкости по трубке с изменяющим поперечным сечением, не учитывая трение

Жидкость затекает в часть трубки с сечением S ₁ со скоростью υ ₁ и протекает через участок с сечением S ₂ со скоростью υ ₂ .За короткий промежуток времени Δt через площадь S ₁ протечет вода массой m ₁ , через площадь S ₂ протечет вода массой m ₂ . По закону сохранения массы m ₁ = m ₂ .. Если вместо массы воды поставить плотность ρ и объем воды V, получим:

Полученный результат можно сформулировать следующим образом:

Модули скоростей несжимаемой жидкости, текущей по трубам с разными сечениями, обратно пропорциональны сечениям трубы

Это называется уравнением непрерывности течения для несжи маемой жидкости .

Таким образом, в широком месте трубки скорость жидкости будет меньше, чем в узком месте. Например, когда нужно, чтобы вода из водопроводного шланга брызгала дальше, нужно сжать отверстие шланга.

Пусть вода течет по трубе разного сечения, с тонкими измерительными трубками наверху . При стационарном течении жидкость по измерительным трубкам поднимается вверх. По высоте подъема жидкости можно сделать вывод об оказываемом ею на стенки трубы давлении. Опыты показывают что в широких местах трубы давление будет больше, чем в узких местах. Согласно уравнению непрерывности течения, скорость течения в широкой части будет меньшей, а в узкой части будет больше. На основании вышеизложенного можно сделать следующий вывод:

Математическое выражение зависимости давления жидкости от скорости течения . определил в 1738 году Д. Бернулли.

Уравнение Бернулли можно вывести из закона сохранения меха нической энергии применительно к течению жидкости.

У ста но в и м т р у б к у с и з м е н я ю щи м с я с еч е н и е м , п о к от о р о й т еч е т жидкость, под наклоном относительно горизонта

У ста но в и м т р у б к у с и з м е н я ю щи м с я с еч е н и е м , п о к от о р о й т еч е т жидкость, под наклоном относительно горизонта.

На широком отрезке трубки за время t

через сечение АВ протекает определенный объем жидкости. Поскольку жидкость считается несжимаемой, через сечение CD за это время протекает такое же количество жидкости. Обозначим площадь сечения АВ как S _1, скорость течения жидкости через это сечение υ ₁ , соответственно площадь сечения CD обозначим S ₂ и скорость υ ₂

Сила давления F ₁ и F _{2 .} Под действием силы тяжести выделенный объем жидкости в течение времени t смещается в правую сторону из-за разности давлений .

.Согласно закону сохранения энергии выполненная работа внешних сил равна изменению энергии:

Это выражение называется уравнением Бернулли для течения идеальной жидкости или газа

1.Емкость имеет на дне маленькое отверстие закрытое пробкой. В емкость залили воду высотой 1 м. На поверхности воды установили поршень массой 1 кг и площадью 100 см 2 . Через стенки емкости и поршня вода не просачивается. С какой скоростью будет выливаться вода, если резко открыть пробку

Видео:Закон БернуллиСкачать

Движение жидкости уравнение бернулли конспект

Документальные учебные фильмы. Серия «Физика».

Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 — 17 марта 1782), швейцарский физик-универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Сын Иоганна Бернулли.

Закон (уравнение) Бернулли является (в простейших случаях) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

— плотность жидкости, — скорость потока, — высота, на которой находится рассматриваемый элемент жидкости, — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, — ускорение свободного падения.

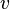
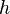
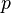
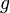
Уравнение Бернулли также может быть выведено как следствие уравнения Эйлера, выражающего баланс импульса для движущейся жидкости.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли(не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли или интегралом Бернулли.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Соотношение, близкое к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы высота постоянна и уравнение Бернулли принимает вид: .

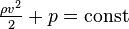
Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .

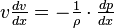
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического и динамического давлений.

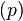
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений), в магнитной гидродинамике, феррогидродинамике.

В статье были спользованны материалы Wikipedia

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

План-конспект урока физики в 9-м классе по теме: «Принцип Бернулли. Закон Бернулли»

Разделы: Физика

Цели:

Изучить законы движения жидкостей и газов на основе закона сохранения энергии, дать определение принципа Бернулли, рассмотреть проявление закона Бернулли в природе и использование в технике и быту.

Развивать знания, умения, навыки учащихся, способы мышления, физическую речь, память.

Формировать научное мировоззрение, воспитывать интерес и любознательность учащихся, способность самостоятельно наблюдать явления и делать выводы.

Демонстрации:

Полоски бумаги.

Компьютерная модель (диск “Открытая физика”).

Шарики для тенниса, фен.

Цилиндр Магнуса.

Пульверизатор.

Свеча и воронка.

Рисунки.

План.

Актуализация темы.

Скорость движения жидкости по трубе переменного сечения.

Давление внутри потока.

Применение принципа Бернулли в технике, природе, быту.

Лекцию дети фиксируют в тетрадях в таблице, которую мы называем “Ромашкой”. В таблице три столбца: “Известное”, “Новое”, “Специфическое”. Каждый ребенок вносит услышанную информацию в столбец по своему усмотрению, в конце занятия дети обмениваются тетрадями, еще раз прорабатывая материал, вспоминая, что упустил; или выступают с комментариями по просьбе учителя по содержанию одного из столбцов, например, “А мне это было известно…”

До сих пор мы рассматривали движение твердых тел. Знание законов сохранения дает нам возможность познакомиться с основными закономерностями движения жидкостей и газов, которое очень распространено в природе и технике:

Движется воздух в земной атмосфере;
Движется вода в океанах и морях, озерах, реках;
Движется кровь в кровеносных сосудах;
Движутся питательные соки в капиллярах растений;
Движутся вода, нефть, газ в трубопроводах.

Но перед тем, как мы приступим к изучению гидроаэродинамики, дадим слово героям Артура Конан Дойла — Шерлоку Холмсу и доктору Ватсону.

(Сценка в исполнении двух мальчиков.) Холмс читает утреннюю “Таймс”, Ватсон перелистывает какой-то фолиант.

— В каком банке вы храните свои деньги, Ватсон?

— В “Сити-банке”, Холмс, очень надежный банк, уверяю Вас.

— Ваш “надежный банк”, Ватсон, вчера был ограблен!

— Не может этого быть, ведь там все мои сбережения на свадьбу!

— Вот послушайте, что пишет “Лондонская Таймс”: “Пронесшийся вчера над Лондоном ураган выбил все стекла в здании Сити- банка, чем не преминули воспользоваться злоумышленники. Они проникли через разбитые окна в банк и вынесли все деньги. Прибывший на место происшествия инспектор Лестрейд подтвердил это предположение директора банка, так как действительно все окна выбиты, а пол усыпан битым стеклом. Директор банка приносит свои извинения вкладчикам”.

— Это называется – деньги на ветер!

— Дорогой Ватсон, если бы вы изучали физику, вы бы уже знали, у кого ваши деньги.

Учитель: Холмс, в отличие от Ватсона, изучал законы гидроаэродинамики. Познакомимся с ними и мы.

Пусть жидкость течет без трения по трубе переменного сечения:

Иначе говоря, через все сечения трубы проходят одинаковые объемы жидкости, иначе жидкости пришлось бы либо разорваться где-нибудь, либо сжаться, что невозможно. За время t через сечение S₁пройдет объем

, а через сечение S₂ – объем . Но так как эти объемы равны, то

Скорость течения жидкости в трубе переменного сечения обратно пропорциональна площади поперечного сечения. Если площадь поперечного сечения увеличилась в 4 раза, то скорость уменьшилась во столько же раз и наоборот, во сколько раз уменьшилось сечение трубы, во столько же раз увеличилась скорость течения жидкости или газа. Где наблюдается такое явление изменения скорости? Например, на реке, впадающей в море, наблюдается уменьшение скорости, вода из ванны — скорость увеличивается, мы наблюдаем турбулентное течение воды. Если скорость невелика, то жидкость течет как бы разделенная на слои (“ламиниа” – слой). Течение называется ламинарным.

Вывод 1: В широкой части трубы скорость меньше, чем в узкой части во столько раз, во сколько раз площадь поперечного сечения 1 больше 2.

Итак, выяснили, что при течении жидкости из узкой части в широкую или наоборот, скорость изменяется, следовательно, жидкость движется с ускорением. А что является причиной возникновения ускорения? (Сила (второй закон Ньютона)). Какая же сила сообщает жидкости ускорение? Этой силой может быть только разность сил давления жидкости в широкой и узкой частях трубы.

К этому выводу впервые пришел академик Петербургской академии наук Даниил Бернулли в 1726 году и закон теперь носит его имя.

Уравнение Бернулли показывает, что давление текущей жидкости или газа больше там, где скорость меньше, и давление меньше там, где скорость течения больше. Этот казалось бы парадоксальный вывод подтверждается прямыми опытами.

А) У вас на столах есть листки бумаги. Возьмите один из них за короткую сторону и подуйте вдоль листа. Лист… поднимается вверх. Почему? Потому что в струе воздуха, продуваемом над листом скорость больше, чем под листом, а давление меньше, чем под листом. Эта разность давлений и поднимает лист вверх! Б)Если продувать воздух между двумя листами, то они станут сближаться. Так как давление между листами меньше, чем снаружи, и внешнее избыточное давление сближает листки.

Если взять трубку переменного сечения и присоединить к ней манометрические трубки , то мы увидим, что в узких частях трубки, где скорость больше, давление будет меньше и уровень жидкости в манометре будет невысоким, наоборот, в широкой части трубы, там где скорость мала, давление большое и уровень жидкости в трубке будет больше. (Компьютерная модель)

Опыт 2. Проделаем похожий опыт. Будем продувать с помощью фена воздух между двумя теннисными шарами — что произойдет? (шарики сближаются). Шарики станут сближаться. Если в струю воздуха положить легкий теннисный шарик, то он будет “плясать” в струе, даже если её расположить слегка наклонно. Почему? (Давление в комнате будет велико по отношению к давлению воздуха в струе, и разница давлений будет удерживать шарик в струе.)

Опыт 3. Склеим из тонкой бумаги цилиндр, обвяжем его ленточкой и резко дернув палочку, заставим цилиндр вращаться против часовой стрелки и двигаться вперед. Цилиндр при этом поднимается почти до потолка, а затем плавно опускается на пол. Почему это происходит?

(Цилиндр, вращаясь, движется вперед. При вращении цилиндра в движение приходит и прилежащий к нему слой воздуха. Но под цилиндром вектор скорости воздуха антипараллелен вектору скорости цилиндра, а над цилиндром – сонаправлен с ним. Поэтому результирующая скорость воздуха под цилиндром меньше, чем над ним, следовательно, давление больше, и разность давлений поднимает цилиндр вверх, а не по параболе, как мы привыкли, в механике.)

Это явление носит название эффекта Магнуса, по имени ученого, открывшего и исследовавшего его экспериментально. Эффект Магнуса проявляется в таких природных явлениях, как образование смерчей над поверхностью океана. В месте встречи двух воздушных масс с разными температурами и скоростями возникает вращающийся вокруг вертикальной оси столб воздуха и несется вперед. В поперечнике такой столб может достигать сотен метров и несется со скоростью около 100м/с. Из-за быстрого вращения воздух отбрасывается к периферии вихря и давление внутри него понижается. Когда такой столб приближается к воде, то засасывает ее в себя, представляя огромную опасность для судов. Это же явление знают железнодорожники и предписывают встречным поездам сбрасывать скорость. Зачем? (Дело в том, что перед идущим поездом создается область сжатого воздуха (большое давление), а за другим поездом создается область пониженного давления. При этом, во-первых, могут разбиться стекла в вагонах из-за большой разности давлений, во-вторых, если человек или животное окажется между путями в этот момент, то его может затянуть под поезд, поэтому необходимо помнить правила поведения в таких ситуациях: нужно либо обхватить покрепче опору – столб, например, либо распластаться на земле и сильнее вжаться в нее всем телом, чтобы избежать трагедии.)

Опыт 4. (Обсуждение и рисунок)

В дождливую и ветреную погоду, наверное, каждый из вас замечал, что раскрытые зонтики иногда “выворачиваются наизнанку”. Почему это происходит? Поток воздуха, набегающий на изогнутую поверхность зонта, движется по руслу своеобразной сужающейся трубы с большей скоростью, чем воздух в нижней части, следовательно, давление снизу больше, чем вверху, и зонт выворачивается!

Опыт 5. (Обсуждение). Аналогичное действие производит на крыши домов сильный ураган. Кстати, по поводу урагана. Так у кого же деньги, мистер Холмс? (Ураган, пронесшийся по улицам Лондона, должен был привести к тому, что стекла в банке выпали бы на улицу, вследствие явления Бернулли. А так как пол в банке был предусмотрительно посыпан стеклом, то, видимо, деньги украл тот, у кого были ключи от банка.)

Спасибо, мистер Холмс.

Предлагаю продолжить ролевую игру. Класс делится на группы по три человека, каждой группе выдается задание с рисунком.

Задание 1. Вы – рабочий на английской шахте по добыче угля. Вас попросили закрыть вентиляционный люк специальным щитом. Вы сначала долго боролись со струей воздуха, которая не давала вам подойти к люку, а затем вдруг внезапно притянула вас с такой силой, что захлопнулась щитом, а вы получили тяжкие травмы. Пользуясь рисунком, объясните, пожалуйста, это странное явление. (Кстати, это после происшествия с вами ученые заинтересовались явлениями в струе жидкости или газа.) (В струе воздуха давление мало, а снаружи давление больше, большая разность давлений “толкнула” рабочего в люк и захлопнула его).

Задание 2. Вы – капитан первого самого большого корабля в мире “Олимпик”. Осенью 1912 года вы шли в открытом море, а на расстоянии нескольких метров от вас в том же направлении следовал броненосный крейсер “Гаук” с очень большой скоростью. Когда корабли приняли положение, как показано на рисунке, “Гаук” неожиданно повернулся носом к “Олимпику”, и, не слушаясь руля, пошел ему наперерез.

Произошло столкновение. Когда этот случай рассматривали в морском суде, вас обвинили в том, что вы не дали команду пропустить броненосец. В апреле этого же года затонул двойник вашего корабля – “Титаник”, который не сумел избежать столкновения с айсбергом. Как вы думаете, что произошло? (Пока не строились “плавучие города”, явление Бернулли не наблюдалось на море. В данном случае, между движущимися в одном направлении кораблями образовался канал с текущей в обратную сторону водой. А в струе воды давление меньше, чем вокруг, в покоящемся океане. Огромная разность давлений заставила более легкий корабль врезаться в “плавучий город” “Олимпик”.)

Задание 3. Вы – известный автогонщик Джим Холл. Однажды на гонках вы появились на машине, которую сами и усовершенствовали. Ваш “Чапараль” имел в задней части горизонтальное крыло, плоскость которого была расположена под углом к горизонту, а также два вентилятора, которые засасывали воздух из-под днища и гнали его назад; сбоку автомобиль был закрыт щитками почти до самой дороги. Вас сначала подняли насмех, а когда вы выиграли гонку с большим отрывом, всех заинтересовало ваше изобретение. И сейчас машины часто делают с горизонтальным крылом сзади и с низкой посадкой. Объясните нам, что это дает?

(Воздух, протекающий в маленький просвет между дорогой и авто, как в сужающуюся трубу, ускоряется, давление под машиной уменьшается по сравнению с давлением воздуха над машиной, что ведет к улучшению сцепления шасси с дорогой, что позволяет не сбрасывать скорость на поворотах. Крыло позади автомобиля, обеспечивает “расширение трубы” для воздуха, обтекающего автомобиль сверху, скорость воздуха уменьшается, давление увеличивается, что также влияет на сцепление шасси с дорогой.)

Задание 5. Вы – Николай Егорович Жуковский. Вы разработали теорию подъемной силы крыла самолета, за что вас В.И. Ленин назвал “отцом русской авиации”. Расскажите нам, пожалуйста, почему несимметричная форма сечения крыла самолета, подобно крыльям птиц, позволяет взлетать самолетам? (Из-за несимметричности формы крыла воздух движется по его поверхности с разной скоростью, снизу возникает подъемная сила, равная разности давлений над и под крылом.)

Задание 6. Вы – известный футболист, вы знаете, что когда подают крученый мяч, т.н. “сухой лист”, то мяч летит по искривленной траектории, как заколдованный облетая футболистов, не знающих законов физики. Объясните, нам, в чем тут дело?

(См. эффект Магнуса.)

Работаем по рисункам, иллюстрирующим явления закона Бернулли. (Яйцо втягивается вверх в струю воды, вентиляционная труба с коническим колпаком, форма нор луговых собачек, окруженная конической насыпью, работа газовой горелки, пульверизатора, карбюратора, ветер под зданием, мошки на стекле движущегося автомобиля.)

А сейчас предлагаю соседям по парте обменяться лекциями и посмотреть, что упущено вами или вашим соседом из сегодняшнего урока.

Итог урока. На уроке мы познакомились с законом движения жидкостей и газов – законом Бернулли, в основу вывода которого положен закон сохранения энергии, поэтому этот закон и явления гидроаэродинамики следует рассматривать как следствие из закона сохранения энергии.

Выставление оценок за работу на уроке.

Спасибо за урок!

Рисунки для закрепления материала.