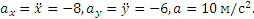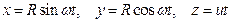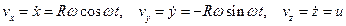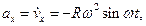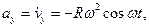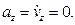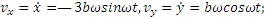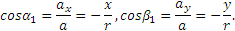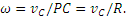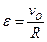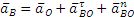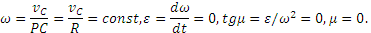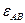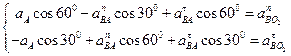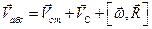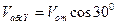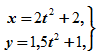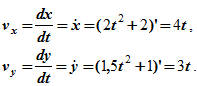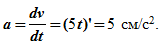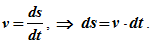Видео:Траектория и уравнения движения точки. Задача 1Скачать
Заданы уравнения движения точки x=3t, y=t2. Определите скорость точки в момент времени t = 2c.
X=3t, Y=t в квадрате, берем производные, получим
Vx=3, Vy=2t
Скорость равна V= квадратный корень из (Vx в квадрате+Vy в квадрате) = квадратный корень из (9+16)= 5.
Как это сложно. Здесь без академика не обойтись
x= 3*2c.
y= 2*2c.
x= 6
y= 4
как сложно 1 класс
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
Задача 2.1.
Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
.
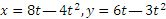
Определить траекторию, скорость и ускорение точки.
Решение.
 |
| Рис. 2.9. К задаче 2.1 |
Для определения траектории исключаем из уравнений движения время t. Умножая обе части первого уравнения на 3, а обе части второго — на 4 и почленно вычитая из первого равенства второе, получим: 
или 
.
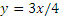
Следовательно, траектория — прямая линия, наклоненная к оси Ох под углом α, где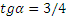 
(рис. 2.9).
Определяем скорость точки. По формулам (2.1) получаем:
;
.
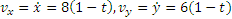
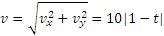
Теперь находим ускорение точки. Формулы (2.1) дают:
Направлены векторы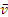 
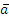
и 
вдоль траектории, т. е. вдоль прямой АВ. Проекции ускорения на координатные оси все время отрицательны, следовательно, ускорение имеет постоянное направление от В к А. Проекции скорости при 0 1 с) обе проекции скорости отрицательны и, следовательно, скорость направлена от В к А, т. е. так же, как и ускорение.
Заметим, наконец, что при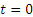 
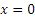
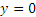
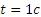
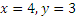
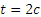
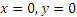
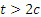
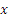
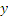
и 
; при 
(точка В); при 
; при 
значения 
и 
растут по модулю, оставаясь отрицательными.
Итак, заданные в условиях задачи уравнения движения рассказывают нам всю историю движения точки. Движение начинается из точки О с начальной скоростью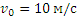 
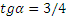
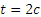
и происходит вдоль прямой АВ, наклоненной к оси Ох под углом α, для которого . На участке OB точка движется замедленно (модуль ее скорости убывает) и через одну секунду приходит в положение В (4, 3), где скорость ее обращается в нуль. Отсюда начинается ускоренное движение в обратную сторону. В момент точка вновь оказывается в начале координат и дальше продолжает свое движение вдоль ОА, Ускорение точки все время равно 10 м/с 2 .
Задача 2.2.
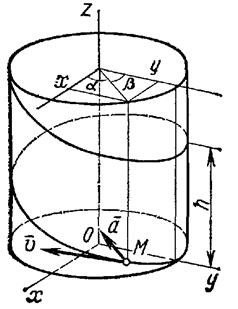
Движение точки задано уравнениями:
где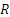 
, ω и u — постоянные величины. Определить траекторию, скорость и ускорение точки.
Решение.
 |
| Рис. 2.10. К задаче 2.2 |
Возводя первые два уравнения почленно в квадрат и складывая, получаем
.
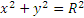
Следовательно, траектория лежит на круглом цилиндре радиуса R, ось которого направлена вдоль оси Oz (рис. 2.10). Определяя из последнего уравнения t и подставляя в первое, находим
.
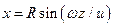
Таким образом, траекторией точки будет линия пересечения синусоидальной поверхности, образующие которой параллельны оси Оу (синусоидальный гофр) с цилиндрической поверхностью радиуса R. Эта кривая называется винтовой линией. Из уравнений движения видно, что один виток винтовой линий точка проходит за время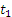 
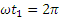
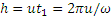
, определяемое из равенства 
. При этом вдоль оси z точка за это время перемещается на величину 
, называемую шагом винтовой линии.
Найдем скорость и ускорение точки. Дифференцируя уравнения движения по времени, получаем:
.
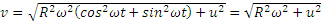
Стоящие под знаком радикала величины постоянны. Следовательно, движение происходит с постоянной по модулю скоростью, направленной по касательной к траектории. Теперь по формулам (2.1) вычисляем проекции ускорения;
.
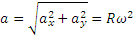
Итак, движение происходит с постоянным по модулю ускорением, Для определения направления ускорения имеем формулы:
,
’
.
,
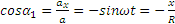
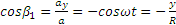
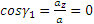
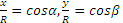
где α и β —углы, образуемые с осями Ох и Оу радиусом R, проведенным от оси цилиндра к движущейся точке. Так как косинусы углов α1 и β1 отличаются от косинусов α и β только знаками, то отсюда заключаем, что ускорение точки все время направлено по радиусу цилиндра к его оси.
Заметим, что хотя в данном случае движение и происходит со скоростью, постоянной по модулю, ускорение точки не равно нулю, так как направление скорости изменяется.
Задача 2.3.
На шестерню 1 радиуса r1 действует пара сил с моментом m1 (рис. 46, а). Определить момент m2 пары, которую надо приложить к шестерне 2 радиуса r2, чтобы сохранить равновесие.
Решение.
 |
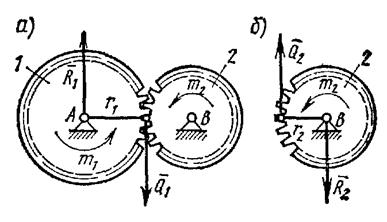| Рис. 2.11. К задаче 2.3 |
Рассмотрим сначала условия равновесия шестерни 1. На нее действует пара с моментом m1, которая может быть уравновешена только действием другой пары, в данном случае пары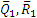 
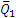
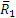
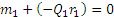
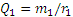
. Здесь 
— перпендикулярная радиусу составляющая силы давления на зуб со стороны шестерни 2, a 
— тоже перпендикулярная радиусу составляющая реакции оси А (сила давления на зуб и реакция оси А имеют еще составляющие вдоль радиуса, которые взаимно уравновешиваются и в условие равновесия не войдут). При этом, согласно условию равновесия (17), 
и 
.
Теперь рассмотрим условия равновесия шестерни 2 (рис. 46, б). По закону равенства действия и противодействия на нее со стороны шестерни 1 будет действовать сила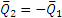 
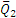
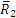
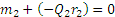
, которая с перпендикулярной радиусу составляющей реакции оси В образует пару 
, 
с моментом, равным -Q2r2. Эта пара и должна уравновеситься приложенной к шестерне 2 парой с моментом m2; следовательно, по условию равновесия, 
. Отсюда, так как Q2=Q1 находим m2=m1/r2r1.
Естественно, что пары с моментами m1 и m2 не удовлетворяют условию равновесия , так как они приложены к разным телам.
Полученная в процессе решения задачи величина Q1 (или Q2) называется окружным усилием, действующим на шестерню. Как видим, окружное усилие равно моменту вращающей пары, деленному на радиус шестерни: Q1=m1/r1 =m2/r2.
Задача 2.4.
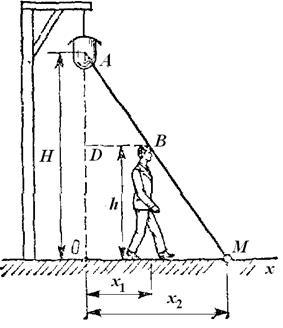
Человек ростом h удаляется от фонаря, висящего на высоте H, двигаясь прямолинейно со скоростью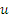 
. С какой скоростью движется конец тени человека?
Решение.
 |
| Рис. 2.12. К задаче 2.4 |
Для решения задачи найдем сначала закон, по которому движется конец тени. Выбираем начало отсчета в точке О, находящейся на одной вертикали с фонарем, и направляем вдоль прямой, по которой движется конец тени, координатную ось Ох (рис. 2.12). Изображаем человека в произвольном положении на расстоянии x1 от точки О. Тогда конец его тени будет находиться от начала О на расстоянии х2.
Из подобия треугольников ОАМ и DAB находим:
.
Это уравнение выражает закон движения конца тени М, если закон движения человека, т.е.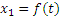 
, известен.
Взяв производную по времени от обеих частей равенства и замечая, что по формуле (2.1)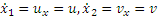 
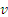
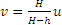
, где 
— искомая скорость, получим
.
Если человек движется с постоянной скоростью (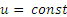 
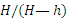
), то скорость конца тени М будет тоже постоянна, но в 
раз больше, чем скорость человека.
Обращаем внимание на то, что при составлении уравнений движения надо изображать движущееся тело или механизм в произвольном положении. Только тогда мы поучим уравнения, определяющие положение движущейся точки (или тела) в любой момент времени.
Задача 2.5.
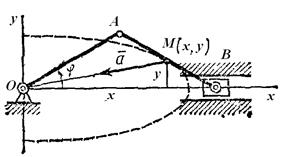
Определить траекторию, скорость и ускорение середины М шатуна кривошипно-ползунного механизма (рис. 2.13), если OA=AB=2b, а угол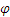 
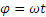
при вращении кривошипа растет пропорционально времени: 
.
 |
| Рис. 2.13. К задаче 2.5. |
Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у находим
.
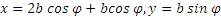
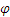
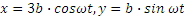
Заменяя его значением, получаем уравнения движения точки М:
.
Для определения траектории точки М представим уравнения движения в виде
.
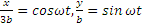
Возводя эти равенства почленно в квадрат и складывая, получим
.
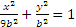
Итак, траектория точки М — эллипс с полуосями 3b и b.
Теперь по формуле (2.1) находим скорость точки М:
.
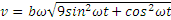
Скорость оказывается величиной переменной, меняющейся с течением времени в пределах от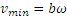 
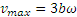
до 
.
Далее по формулам (2.1) определяем проекции ускорения точки М;
;
,
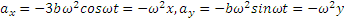
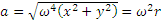
где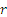 
— длина радиуса-вектора, проведанного из центра О до точки М. Следовательно, модуль ускорения точки меняется пропорционально ее расстояние от центра эллипса.
Определелим направление ускорения
Отсюда находим, что ускорение точки М все время направлено вдоль МО к центру эллипса.
Задача 2.6.
Вал, делающий n=90 об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через t1=40 с. Определить, сколько оборотов сделал вал за это время.
Решение.
Так как вал вращается равнозамедленно, то для него, считая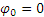 
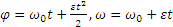
, будет
. (2.2)
Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,
.
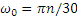
В момент остановки при t=t1 угловая скорость вала ω1=0. Подставляя эти значения во второе из уравнений (2.2), получаем:
и 
.
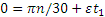
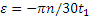
Если обозначить число сделанных валом за время t1 оборотов через N (не смешивать с n; n — угловая скорость), то угол поворота за то же время будет равен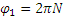 
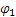
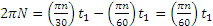
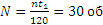
. Подставляя найденные значения ε и 
в первое из уравнений (а), получим
,
.
Задача 2.7.
Маховик радиусом R=0,6 м вращается равномерно, делая n=90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.
Решение.
Скорость точки обода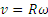 
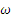
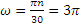
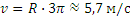
, где угловая скорость 
должна быть выражена в радианах в секунду. Тогда 
и 
.
Далее, так как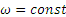 
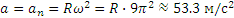
, то ε=0, и, следовательно,
.
Ускорение точки направлено в данном случае к оси вращения.
Задача 2.8.
Найти скорость точки М обода колеса, катящегося по прямолинейному рельсу без скольжения (рис. 2.14), если скорость центра С колеса равна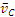 
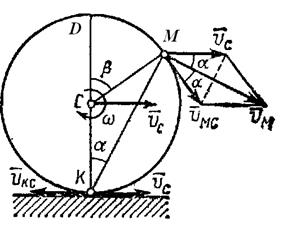, а угол DKM=α.
 |
| Рис. 2.14. К задаче 2.8. |
Решение
Приняв точку С, скорость которой известна, за полюс, найдем, что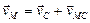 
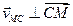
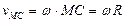
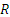
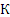
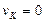
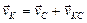
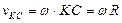
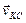
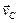
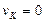
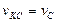
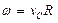
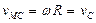
, где 
по модулю 
( 
— радиус колеса). Значение угловой скорости со найдем из условия того, что точка 
колеса не скользит по рельсу и, следовательно, в данный момент времени 
. С другой стороны, так же как и для точки М, 
где 
. Так как для точки К скорости 
и 
направлены вдоль одной прямой, то при 
, откуда 
. В результате находим, что 
.
Параллелограмм, построенный на векторах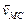 
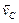
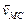
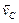
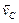
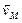
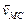
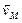
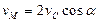
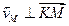
и 
, будет при этом ромбом. Угол между и равен β, так как стороны, образующие этот угол и угол β, взаимно перпендикулярны. В свою очередь угол β=2α, как центральный угол, опирающийся на ту же дугу, что и вписанный угол α. Тогда по свойствам ромба углы между и 
и между и тоже равны α. Окончательно, так как диагонали ромба взаимно перпендикулярны, получим
и 
.
Задача 2.9.
Определить скорость точки М обода катящегося колеса, рассмотренного в предыдущей задаче, с помощью мгновенного центра скоростей.
Решение.
 |
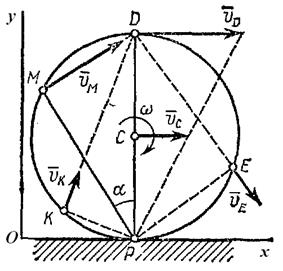| Рис. 2.15. К задаче 2.9. |
Точка касания колеса Р (рис. 2.15) является мгновенным центром скоростей, поскольку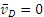 
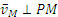
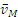
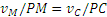
. Следовательно, 
. Так как прямой угол PMD опирается на диаметр, то направление вектора скорости 
любой точки обода проходит через точку D. Составляя пропорцию 
и замечая,
что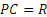 
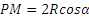
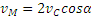
, a 
, находим 
.
Чем точка М дальше от Р, тем ее скорость больше; наибольшую скорость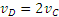 
имеет верхний конец D вертикального диаметра. Угловая скорость колеса имеет значение
Аналогичная картина распределения скоростей имеет место при качении колеса или шестерни по любой цилиндрической поверхности.
Задача 2.10.
Центр О колеса, катящегося по прямолинейному рельсу (рис. 2.16), имеет в данный момент времени скорость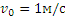 
и ускорение 
. Радиус колеса R=0,2 м. Определить ускорение точки В — конца перпендикулярного ОР диаметра АВ и ускорение точки Р, совпадающей с мгновенным центром скоростей.
Решение.
 |
| Рис. 2.16. К задаче 2.10. |
1) Так как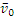 
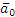
и 
известны, принимаем точку О за полюс.
2) Определение ω. Точка касания Р является мгновенным центром скоростей; следовательно, угловая скорость колеса
.
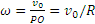
3) Определение ε. Так как величина PO=R остается постоянной при любом положении колеса, то 
Знаки ω и ε совпадают, следовательно, вращение колеса ускоренное.
а) не следует думать, что если по условиям задачи , то 
. Значение 
в задаче указано для данного момента времени; с течением же времени изменяется, так как 
;
б) в данном случае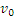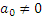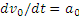 
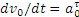
, так как движение точки O является прямолинейным. В общем случае 
.
4) Определение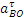 
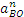
и 
. Так как за полюс взята точка O, то ускорение точки B определяется по фомуле:
Учитывая, что в нашем случае BO=R, находим:
.
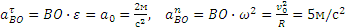
Показав на чертеже точку B отдельно, изображаем (без соблюдения масштаба) векторы, из которых слагается ускорение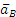 
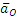
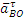
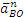
, а именно: вектор 
(переносим из точки O), вектор 
(в сторону вращения, так как оно ускоренное) и вектор 
(всегда от B к полюсу O).
5) Вычисление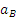 
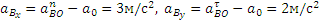
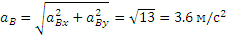
. Проведя оси X и Y, находим, что
,
.
Аналогичным путем легко найти и ускорение точки P: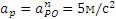 
и направлено вдоль PO. Таким образом, ускорение точки P, скорость которой в данный момент времени равна нулю, нулю не равно.
Задача 2.11.
Колесо катится по прямолинейному рельсу так, что скорость 
его центра С постоянна. Определить ускорение точки М обода колеса (рис. 2.17).
Решение.
 |
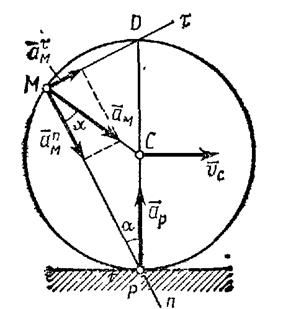| Рис. 2.17. К задаче 2.11. |
Так как по условиям задачи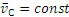 
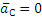
, то 
и точка С является мгновенным центром ускорений. Мгновенный центр скоростей находится в точке Р. Следовательно, для колеса
В результате ускорение точки М
.
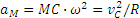
Таким образом, ускорение любой точки М обода (в том числе и точки Р) равно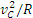 
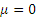
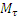
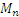
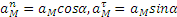
и направлено к центру С колеса, так как угол 
. Заметим, что это ускорение для точки М не будет нормальным ускорением. В самом деле, скорость точки М направлена перпендикулярно РМ . Следовательно, касательная 
к траектории точки М направлена вдоль линии MD, а главная нормаль 
— вдоль МР. Поэтому
.
Зажача 2.12.
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна С, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами (рис.2.17 а). Точка D находится в середине стержня АВ. Длины стержней равны соответственно L1=0,4 м, L2 =1,2 м, L3=1,4 м, L4=0,6 м.
Дано: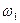 
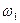
= 6 с -1 , величина постоянная. Заданную угловую скорость считать направленной против часовой стрелки.
Найти: скорости точек В и C; угловую скорость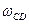 
; ускорение точки В; угловое ускорение 
| а) |  |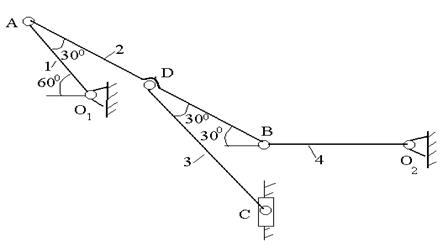
| б) |  |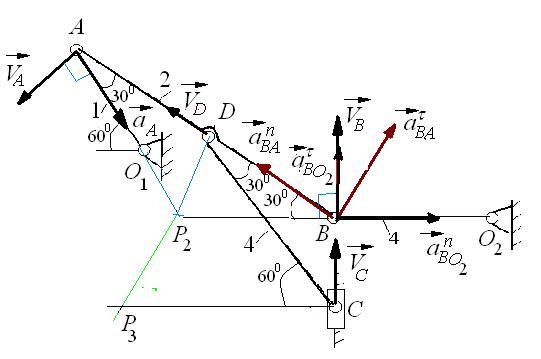
| Рис.2.17. К задаче 2.12. |
Решение (рис.2.12б)
1. Определим скорость точки А. Стержень OAвращается вокруг точко O1, поэтому скорость точки А определяется по формуле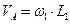 
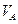
= 1,6 м/с и направлена перпендикулярно отрезку O1А. 
= 1,6 м/с
2. Определим угловую скорость стержня АВ. Точка В вращается вокруг центра О2, поэтому ее скорость перпендикулярна отрезку O2B. Для нахождения мгновенного центра скоростей отрезка АВ в точках А и В восстановим перпендикуляры к векторам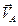 
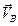
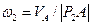
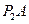
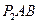
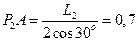
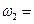
и 
. Точка пересечения этих перпендикуляров Р2 является мгновенным центром скоростей второго стержня. Угловая скорость вычисляется по формуле 
. Расстояние 
определяется из равнобедренного треугольника 
, то есть 
м. Поэтому 
2,3 с -1 .
3. Определим скорость точки В по формуле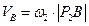 
= 1,6 м/с
по формуле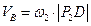 
= 0,8 м/с
4. Определим скорость точки С. Так как точка С движется прямолинейно, то ее скорость направлена вдоль движения ползуна. Для нахождения мгновенного центра скоростей отрезка CD в точках C и D восстановим перпендикуляры к векторам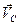 
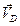
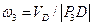
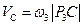
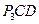
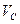
и 
. Точка пересечения этих перпендикуляров Р3 является мгновенным центром скоростей третьего стержня. Угловая скорость вычисляется по формуле 
, а скорость точки С 
. Так как треугольник 
равносторонний, то 
= 0,8 м/с
5. Определим угловую скорость отрезка О2В. Известно, что центром скоростей этого стержня является точка О2В , а также скорость точки B. Поэтому угловая скорость четвертого стержня вычисляется по формуле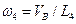 
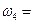
и 
2,7 с -1 .
6. Определим ускорение точки А. Так как первый стержень вращается равномерно, то точка А имеет относительно О1 только нормальное ускорение, которое вычисляется по формуле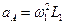 
= 6,4 м/с 2 .
7. Определим ускорение точки В, которая принадлежит двум стержням — АВ и О2В. Поэтому ускорение точки В определяется с помощью двух формул
и 
, где
— ускорение точки А;
— нормальное ускорение точки В относительно А;
— тангенциальное ускорение точки В относительно А;
— нормальное ускорение точки В относительно О2;
— тангенциальное ускорение точки В относительно О2.
= 6,4 м/с 2 ; 
= 4,3 м/с 2 .
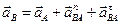
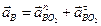
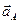
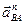
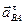
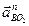
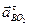
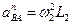
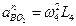
Можно составить уравнение
, которое в проекциях на оси координат имеет вид
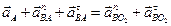
Решив полученную систему двух уравнений с двумя неизвестными, получим:
= 13,2 м/с 2 , аВХ = 4,1 м/с 2 , аВY =9,1 м/с 2 , аВ =10 м/с 2 .
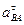
8. Определим угловое ускорение стержня АВ, используя формулу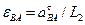 
= 13,2 с -2 .
Задача 2.13.
Круглая пластина радиуса R=60 см вращается вокруг неподвижной оси по закону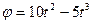 
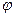
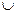
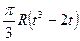
(рис.2.18 а). Положительное направление угла 
показано на рисунке дуговой стрелкой. Ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве). По окружности радиуса R движется точка М. Закон ее движения по дуге окружности s= 
АМ= 
. На рисунке точка М показана в положении, когда s положительно, при s отрицательном точка М находится по другую сторону от точки А; L=R.
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.
| а) |  |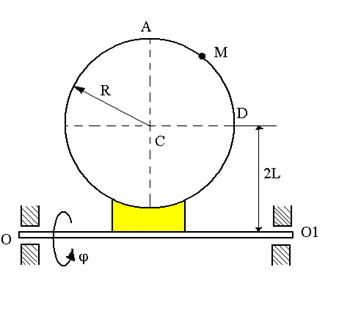
| б) |  |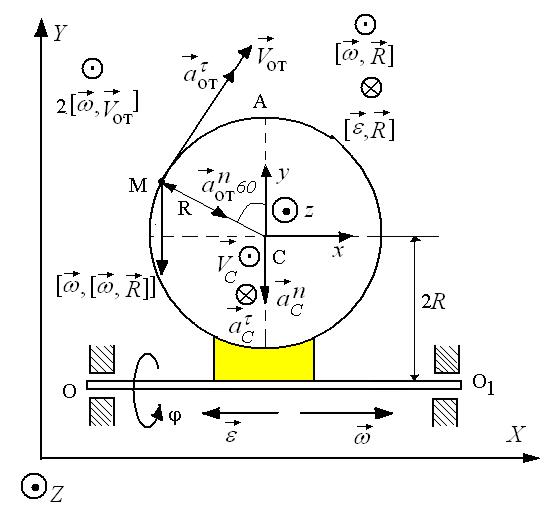
| Рис.2.18. К задаче 2.13. |
Решение (рис.2.13 б)
В качестве подвижной системы координат xyz примем точку С. Эта система совершает вращательное движение с угловой скоростью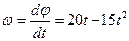 
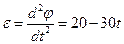
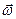
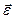
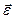
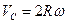
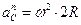
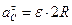
= 5 с -1 . Угловое ускорение 
= -10 с -2 . Направления векторов 
и 
опледеляются по правилу буравчика и изображены на рис. Причем, вектор направлен в противоположную сторону, так как его значение его проекции на ось OХ неподвижной системы координат XYZ отрицательно. Вычислим скорость и ускорение центра подвижной системы координат С, которая движется по окружности. Скорость вычисляется по формуле 
, равна 600 см/с и первендикулярна плоскости рисунка. Ускорение точки С состоит из двух компонент — нормальное 
= 3000 см/с 2 и тангенциальное 
= 1200 см/с 2 ускорения.
Вычислим путь, относительную скорость и ускорение точки M. Ее положение определяется величиной дуги S, в данный момент времени S =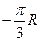 
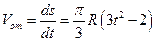
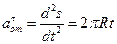
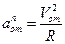
, поэтому она располагается слева от точки А. Относительная скорость 
. В данный момент времени она равна 63 см/с и направлена по касательной к окружности. Относительное ускорение является суммой двух составляющих — тангенциальное 
= 377 см/с -2 и нормальное 
= 66 см/с -2 .
Абсолютная скорость точки M определяется по формуле
Где —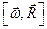 
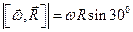
переносная скорость вращательного движения, модуль которой 
= 150 см / с, ее направление определяется по правилу Жуковского. В разложении на оси координат
По теореме Пифагора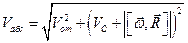 
= 750 м /с.
Абсолютное ускорение точки M определяется по формуле
Где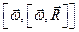 
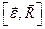
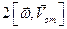
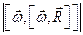
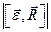
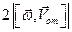
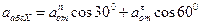
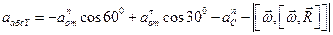
и 
— соответственно нормальное и тангенциальное переносные ускорения вращательного движения, 
— кориолисово ускорение.
= 750 м / с -2 ; 
=300 м / с -2 ; 
= 546 м / с -2
;
;
Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать
iSopromat.ru
Пример решения задачи по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в некоторые моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать
Задача
где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t0=0 с, t1=1 с и t2=5 с, а также путь, пройденный точкой за 5 с.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Решение
Расчет траектории
Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:
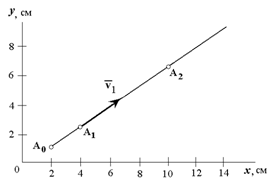
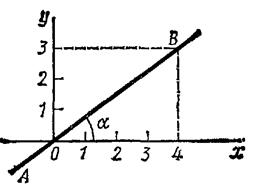
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).
Для того, чтобы определить координаты начального положения точки A0, подставим в заданные уравнения значения t0=0; из первого уравнения получим x0=2 см, из второго y0=1 см. При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A0 (2; 1).
Расчет скорости
Расчет ускорения
Определяем ускорение точки. Его проекции на оси координат:
Проекции ускорения не зависят от времени движения,
т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.
С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:
Определение пути
Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:
Проинтегрируем последнее выражение:
Если t=t0=0, то C=s0; в данном случае s0=0, поэтому s=2,5t 2 . Находим, что за 5с точка проходит расстояние
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
💥 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
График функции y=x² (y=аx).Скачать
Математика это не ИсламСкачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
12. Уравнения прямой в пространстве Решение задачСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Уравнение плоскости через 2 точки параллельно векторуСкачать
Решение графических задач на равномерное движениеСкачать
ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать
11 класс, 8 урок, Уравнение плоскостиСкачать
9 класс, 6 урок, Уравнение окружностиСкачать
Кинематика точки в плоскости. ТермехСкачать
Составляем уравнение прямой по точкамСкачать
