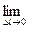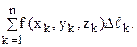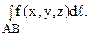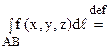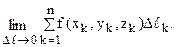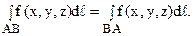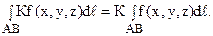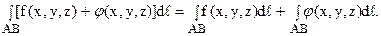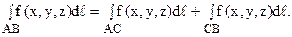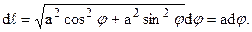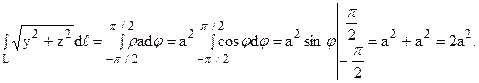Движение точки по кривой задано уравнением r ia1t 3 j a2t (4 видео)

Криволинейные интегралы первого рода (по длине дуги) – КИПР.

Пусть в пространстве Oxyz задана непрерывная спрямляемая кривая АВ, в точках которой определена произвольная функция f(x, y, z). Проделаем 5 операций:

1. Разобьем кривую АВ на n частей точками М₁, М₂, ….М_n-1, следующими друг за другом в направлении от А к В (для определенности). Точку А обозначим через М₀, точку В через М_n. Длины дуг М_k-1 М_k (k = 1, 2,…, n) обозначим, соответственно, через . Наибольшую из величин
(k = 1, …, n) обозначим через 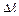и назовем рангом (шагом) дробления кривой АВ.

2. На каждой дуге М_k-1 М_k (k = 1, 2, …, n) выберем произвольным образом по точке N_k(x_k; y_k; z_k) и вычислим в них значения функции
f(x, y, z), т.е. найдем числа f(x_k, y_k, z_k).

3. Вычислим произведения f(x_k, y_k, z_k) (k = 1, 2, …, n).

4. Найдем сумму 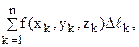которую называют интегральной суммой для функции f(x, y, z) на кривой АВ, отвечающей данному разбиению (дроблению) АВ на части и выбору точек N_k (x_k; y_k; z_k).

5. Измельчая дробление, ищем предел

( 1)

Если существует конечный предел ( 1), не зависящий ни от способа дробления кривой АВ на части, ни от выбора точек N_k(x_k; y_k; z_k) (k = 1, 2, …, n), то этот предел называют криволинейным интегралом первого рода (по длине дуги) от функции f(x, y, z) по дуге АВ и обозначают символом:

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

При этом функцию f(x, y, z) называют подынтегральной функцией, кривую АВ – линией (кривой, контуром) интегрирования, точку А – начальной, а точку В – конечной точками интегрирования (тем самым устанавливается направление интегрирования).

Таким образом, по определению

( 2)

Перечислим простейшие свойства криволинейного интеграла первого рода (в основном аналогичные свойствам определенного интеграла):

1. Значение криволинейного интеграла первого рода не зависит от направления на кривой:

2. Постоянный множитель в подынтегральной функции можно выносить за знак криволинейного интеграла:

3. Криволинейный интеграл первого рода от суммы двух функций равен сумме интегралов от этих функций:

Видео:Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

4. Если кривая АВ разбита точкой С на две части АС и СВ, то криволинейный интеграл по всей кривой АВ равен сумме интегралов по ее частям:

5. Если в каждой точке кривой АВ функции f(x, y, z) и j(x, y, z) удовлетворяют неравенству f(x, y, z) 2 + z 2 = ay (a > 0).

Введем полярные координаты: y = rcosj, z = rsinj .

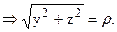
Уравнение окружности принимает вид: r 2 = arcosj или r = acosj.

Тогда r’ = -asinj и

Т. к. окружность расположена в той части плоскости yOz, где y > 0, то угол j меняется от -p/2 до p/2. По формуле ( 7) имеем:

Пример 3.

Вычислить 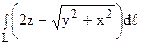, где L – дуга кривой, заданной параметрически:
x = tcost, y = tsint, z = t (0 2 , 0 3 = 3a 2 y, 2xz = a 2 , заключенной между плоскостями y = 9a,
y = a/3.

Длину дуги L можно записать в виде : .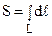

Приняв за параметр координату х, уравнения данной линии можно представить в параметрическом виде: x = t, y = t 3 /3a 2 , z = a 2 /2t. Значения параметра, соответствующие концам рассматриваемой дуги, вычисляются по формуле: 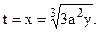Таким образом,
t₁ = a, t₂ = 3a.