Про уравнения - легко » Статьи

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Обновлено
Содержание
  1. Пример выполнения курсового задания К 4
  2. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
  3. Дифференциальные уравнения относительного движения материальной точки
  4. Кинематика точки
  5. 🔥 Видео

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Траектория и уравнения движения точки. Задача 1

Пример выполнения курсового задания К 4

Дано: уравнение относительного движения точки М

уравнение вращательного движения тела D

t1 = 1 c; R = 40 см.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид
Точка М движется по телу D. По заданным уравнениям относительного движения точки М и движения тела D определить для заданного момента времени t1 абсолютную скорость и абсолютное ускорение точки М (OM(t1) = ? Vr(t1) = ? Ve(t1) = ? V(t1) = ? ar(t1) = ? ae(t1) = ? ac(t1) = ? a(t1)= ?) (рис. 2.49).

Решение. Точка М осуществляет сложное движение, поэтому для решения задачи необходимо ввести неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ. Изобразим рассматриваемый механизм в момент времени t1 (рис. 2.50).

Координатную ось O1Y1 неподвижной системы отсчёта направим по оси вращения тела D. Подвижную систему отсчёта OXYZ закрепим на теле D, расположив начало отсчёта в точке О. По исходным данным уравнение относительного движения точки М задано естественным способом Sr(t) = 2,5·p·t 2 . Исходя из этого, известны следующие характеристики движения: вид траектории движения – дуга окружности радиусом R; начало отсчёта дуговой координаты Sr – точка О; положительное направление отсчёта дуговой координаты Sr – знак (+); уравнение движения Sr = 2,5·p·t 2 .

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Определим положение точки М на траектории относительного движения в момент времени t1:

Для координации точки М на траектории относительного движения целесообразно использовать центральный угол:

Итак, α(t1) = 45 о . Точка М тела D, совершающего вращательное движение в неподвижной системе отсчёта O1X1Y1Z1, описывает окружность радиусом

MK = R – R·cos(α(t1)) = R·(1 – cos(α(t1))= 40·(1 – 0,707) = 11,72 см.

Таким образом, траектория переносного движения точки М установлена. Это окружность радиусом МК с центром в точке К, расположенной на оси вращения тела D.

Абсолютное движение точки М – это сумма относительного и переносного движений. Таким образом, траектория абсолютного движения точки М представляет собой винтовую линию, расположенную на сферическом конусе.

Для определения абсолютной скорости V точки М используется векторное равенство

где Vr – вектор относительной скорости; Ve – вектор переносной скорости.

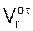
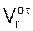
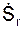
Определим проекцию Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видотносительной скорости Vr на касательную:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 5·p·t.

В момент времени t1 имеем

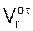
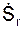
Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = 5·p·t1 = 5·p·2 = 10·p = 31,4 см/c > 0.

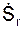
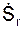
Поскольку Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) > 0, то модуль относительной Vr(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), а вектор относительной скорости Vr направлен так же, как и единичный вектор τ естественной координатной системы отсчёта. Покажем этот вектор на рис. 2.50.

Для определения переносной скорости Ve предварительно найдем модуль ωе угловой скорости 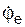Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видпереносного вращения.

ωe = I 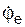Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видI = I6·t 2 – 5I.

В момент времени (t1) имеем

ωe(t1) = I6·(t1) 2 – 5I = I6·2 2 – 5I = 19 рад/c > 0.

Поскольку ωe(t1) > 0, то величина угла φе возрастает. Покажем на рис. 2.50 направление вращения и определим модуль переносной скорости Ve(t1) по формуле

Так как Ve(t1) направлена по касательной к траектории переносного движения, то она перпендикулярна плоскости OYZ подвижной системы отсчёта. С другой стороны, Vr ┴ Ve. Исходя из этого, определим модуль абсолютной скорости:

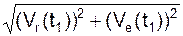
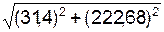
V(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 224,88 см/с.

Если Vr не перпендикулярна Ve, то определение модуля скорости V следует определять через проекции векторного выражения V = Vr + Ve на координатные оси неподвижной системы отсчёта O1X1Y1Z1.

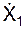
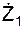
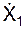
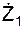
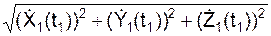
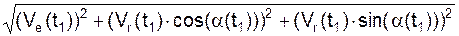
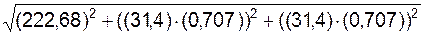
Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= Ve; Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= – Vr·cos(α); Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= Vr·sin(α),

где Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид, Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид, Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид– проекции абсолютной скорости на оси O1X1, O1Y1, O1Z1 системы отсчёта O1X1Y1Z1.

V(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид=

= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид=

= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 224,88 см/с.

Для ориентации абсолютной скорости Vв пространстве неподвижной системы отсчёта определим направляющие косинусы.

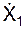
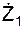
cos(V,i1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/V(t1) = 222,68/224,88 = 0,990;

cos(V,j1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/V(t1) = (– 31,4·0,707)/224,88 = – 0,098;

cos(V,k1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/V(t1) = (31,4·0,707)/224,88 = 0,098.

При определении абсолютного ускорения a точки М используется формула

где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.

Поскольку относительное движение задано естественным способом, то справедливо равенство

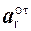
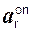
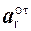
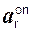
ar = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид,

где Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид– относительное касательное ускорение; Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид– относительное нормальное ускорение.

Так как переносное движение является вращательным, то переносное ускорение ae находят по формуле

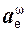
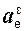
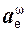
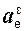
ae = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид,

где Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид– переносное центростремительное ускорение; Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид– переносное вращательное ускорение.

Исходную формулу для определения абсолютного ускорения можно представить в следующем виде:

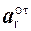
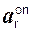
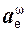
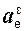
a = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ ac .

Приступаем к определению слагаемых в правой части последнего выражения.

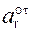
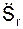
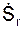
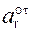
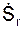
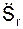
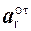
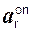
Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= d Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид/dt = d(5·p·t)/dt = 5·p = const.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = 5·p = 5·3,14 = 15,7 см/с 2 > 0 = const.

Так как Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют види Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видимеют одинаковые знаки, то в относительном движении точка М движется равноускоренно. Покажем вектор Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) на рис. 2.50.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)= (Vr(t1)) 2 /ρ = (Vr(t1)) 2 /R = (3,14) 2 /40 = 24,64 см/с 2 .

Вектор Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) направлен по главной нормали к центру кривизны траектории относительного движения.

Модуль ar(t1) относительного ускорения ar(t1) в момент времени t1 определим по формуле

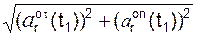
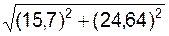
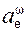
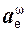
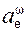
ar(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид=

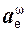
= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 29,276 cм/c 2 .

Модуль Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) переносного центростремительного ускорения Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) в момент времени t1 определим по формуле

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = (ωe(t1)) 2 ·MK = (19) 2 ·11,72 = 4230,92 см/с 2 .

Вектор Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) направлен к оси переносного вращения. Покажем его на рис. 2.50.

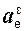
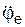
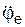
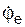
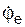
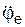
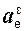
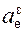
Для определения переносного вращательного ускорения Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют виднеобходимо предварительно определить модуль εе переносного углового ускорения Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид.

εe = I Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видI = Id Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид/dtI = Id(6·t 2 – 5)/dtI = I12·tI.

Так как Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют види Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видимеют одинаковые знаки, то переносное вращение происходит ускоренно. Исходя из этого, направления Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют види Ve совпадают.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с 2 .

Покажем вектор 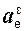Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) на рис. 2.50.

Модуль ae(t1) переносного ускорения aе(t1) в момент времени t1 определим по формуле

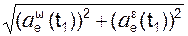
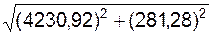
aе(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид=

= Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 4240,259 cм/c 2 .

Приступаем к определению модуля ускорения Кориолиса.

ac(t1) = 2ωе(t1)·Vr(t1)·sin( 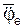Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), Vr(t1)).

Согласно определению вектор 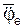Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видпереносной угловой скорости лежит на оси вращения тела D и направлен в сторону увеличения координаты Y1 (см. рис 2.50).

ac(t1) = 2ωе(t1)·Vr(t1)·sin( 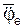Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), Vr(t1)) = 2ωе(t1)·Vr(t1)·sin(135 o ) =

= 2·19·31,4·0,707 = 843,59 см/с 2 .

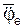
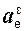
По правилу векторного произведения (ac = 2( Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видxVr)) ускорение Кориолиса ac направлено так же, как и векторы Ve и Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид. Покажем вектор ускорения Кориолиса на рис. 2.50.

Таким образом, в векторном равенстве

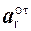
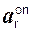
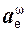
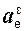
a = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид+ ac

известны все слагаемые, находящиеся в его правой части.

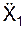
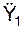
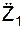
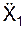
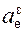
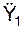
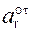
Определим модуль a(t1) абсолютного ускорения a(t1) через его проекции Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) + ac(t1) = 281,28 + 843,59 = 1124,87 см/с 2 ;

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = – Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)·cos(α(t1)) + Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)·sin(α(t1)) =

= – 15,7·0,707 + 24,64·0,707 = 6,32 см/с 2 ;

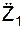
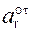
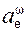
Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)·sin(α(t1)) + Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)·cos(α(t1)) – Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1) =

= 15,7·0,707 + 24,64·0,707 – 4230,92 = – 4202,39 см/с 2 ;

a(t1) = 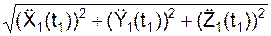Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид= 4350,01 см/с 2 .

Для ориентации абсолютного ускорения в пространстве определим направляющие косинусы.

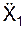
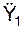
cos(a, i1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/a(t1) = 1124,87/4350,01 = 0,258;

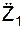
cos(a, j1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/a(t1) = 6,32/4350,01 = 0,001;

cos(a, k1) = Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1)/a(t1) = – 4202,39/4350,01 = – 0,966.

Результаты расчётов сводятся в таблицу.

Кинематические характеристики точки М в момент времени t1

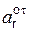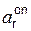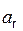Sr(t1), смVr(t1), см/сVe(t1), см/сV(t1), см/с Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), см/с 2 Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), см/с 2 Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид(t1), см/с 2
31,40031,400222,688224,88015,70024,64029,276
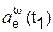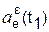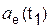Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид, см/с 2 Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид, см/с 2 Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид, см/с 2ωe(t1), рад/сεe(t1), рад/с 2ac(t1), см/с 2a(t1), см/с 2
4230,920281,2804240,25919,00024,000843,5904350,010

2.28. Сферическое движение твёрдого тела

Рассмотрим движение тела, одна из точек которого во всё время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называют сферическим движением твёрдого тела.

Сферическое движение твёрдого тела – движение, при котором скорость одной точки тела равна нулю, а остальные точки движутся по сферическим поверхностям, центры которых совпадают с этой неподвижной точкой.

Примером сферического движения тела служит движение волчка, имеющего неподвижную точку О1 (рис. 2.51).

Для определения положения тела в каждый момент времени используют две системы отсчёта: неподвижная система отсчёта O1X1Y1Z1 и подвижная система отсчёта OXYZ, которая жёстко закреплена на теле. При этом начало отсчёта ПСО совпадает с началом отсчёта НСО.

На рис. 2.51 стрелками показаны положительные направления отсчёта углов Ψ, φ, и θ. Рассмотрим подробнее порядок отсчёта этих углов. Плоскость OXY подвижной системы отсчёта OXYZ пересекается с плоскостью O1X1Y1 неподвижной системы отсчёта O1X1Y1Z1 по линии O1L. Эту линию называют осью узлов. Введём единичный вектор р, направленный от точки О1 к точке L оси узлов. Единичные векторы i1, p лежат в горизонтальной плоскости O1X1Y1 и образуют угол Ψ, величина которого зависит от времени. Ψ = f1(t). Положительное направление отсчёта угла Ψ определяют по правилу: смотря навстречу вектору k1, поворот вектора i1 к вектору р должны увидеть происходящим против хода часовой стрелки.

Единичные векторы k1, k образуют плоскость, в которой находится угол θ, который также зависит от времени. θ = f2(t). Положительное направление отсчёта угла θ определяют по правилу: смотря навстречу вектору i, поворот вектора k1, к вектору k должны увидеть происходящим против хода часовой стрелки.

Единичные векторы р, i образуют плоскость, в которой лежит угол φ, величина которого зависти от времени. φ = f3(t). Правило положительного направления отсчёта угла φ: смотря навстречу вектору j, поворот вектора р к вектору i должны увидеть происходящим против хода часовой стрелки.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Углы Ψ, θ, φ называют также эйлеровыми углами:

угол Ψ – угол прецессии;

угол θ – угол нутации;

угол φ – угол собственного вращения.

Так как положение тела, имеющего одну неподвижную точку, определяется тремя эйлеровыми углами, т. е. тремя параметрами, то оно имеет три степени свободы.

Таким образом, сферическое движение тела описывается тремя уравнениями движения:

При сферическом движении широко используют теорему Эйлера-Даламбера.

Твёрдое тело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг оси, проходящей через неподвижную точку (рис. 2.52).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Другими словами, тело может вращаться относительно мгновенной оси вращения.

Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю.

В случае сферического движения вектор угловой скорости Ω в данный момент времени откладывается от неподвижной точки О по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.

Tело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку. Примером такого движения является качение подвижного конуса 1 по неподвижному конусу 2 (рис. 2.53). Покажем на рисунке направление вектора мгновенной угловой скорости и запишем формулу для определения модуля скорости точки С подвижного конуса.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Так как скорость VО точки О конуса 1 равна нулю, то этот конус совершает сферическое движение. Такое движение можно представить как вращательное движение относительно мгновенной оси вращения. Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю. Для тела 1 мгновенной осью вращения является ось ОК (см. рис. 2.53).

Вектор Ω угловой скорости тела 1 откладывается на мгновенной оси вращения в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.

Модуль VC скорости точки С конуса 1 определяют по формуле

где CL – кратчайшее расстояние от точки С тела 1 до мгновенной оси вращения.

Для заочной и дистанционной форм обучения выполнение контрольных работ на сферическое движение не предусмотрено. Однако такие задачи довольно часто встречаются в дидактических единицах интернет–экзамена. Приведём примеры решения задач такого типа.

Подвижный конус катится по неподвижной горизонтальной плоскости O1X1Y1, имея неподвижную точку О1 (рис. 2.54).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид
Запишите номер вектора, по которому направлена мгновенная угловая скорость вращения.

Ответ. Мгновенная угловая скорость вращения Ω совпадает с направлением 1.

Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси О1С относительно оси О1С1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.55).

(Для справки: sin(15 o ) = cos(75 o ) = 0,26; sin(75 o ) = cos(15 o ) = 0,96).

Мгновенная угловая скорость подвижного конуса равна …

Варианты ответов: Ω = 1,9ω1 рад/с; Ω = 2,7ω1 рад/с; Ω = 0,52ω1 рад/с; Ω = 0,35ω1 рад/с; Ω = 0,7ω1 рад/с.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Модуль скорости точки С при вращении оси О1С относительно оси О1С1 определим по формуле VC = ω1·CM = ω1·O1C·sin(30 o ) (рис. 2.56).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен

VC = Ω·CL = Ω·R·cos(15 o ) = Ω·(O1C·tg(15 o ))·cos(15 o ) =

= Ω·O1C·(sin(15 o )/cos(15 o ))·cos(15 o ) = Ω·O1C·(sin(15 o ).

Решая последнее равенство, получим

Ω = ω1·(sin(30 o )/sin(15 o )) = ω1·(0,5/0,26) = 1,93 рад/с.

Правильный ответ: Ω = 1,93 рад/с.

Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси ОС относительно оси ОС1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.57).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид
(Для справки: sin(15 o ) = cos(75 o ) = 0,26; sin(75 o ) = cos(15 o ) = 0,96).

Если известны углы и радиус основания R = 1 м, то мгновенная угловая скорость подвижного конуса 1 равна …

Варианты ответов: Ω = 0,73·ω1 рад/с; Ω = 0,52·ω1 рад/с; Ω = 0,28·ω1 рад/с; Ω = 1,37·ω1 рад/с; Ω = 1,92·ω1 рад/с.

Модуль скорости точки С при вращении оси ОС относительно оси ОС1 определим по формуле VC = ω1·CM = ω1·OC·sin(75 o ) (рис. 2.58).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид
Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен

Решая последнее равенство, получим

Правильный ответ: Ω = 1,37·ω1 рад/с.

2.29. Общий случай движения твёрдого тела

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Рассмотрим движение свободного твёрдого тела в неподвижной системе отсчёта OXYZ (рис. 2.59).

В общем случае движение свободного тела в пространстве можно рассматривать как сумму простейших движений (три поступательных движения, параллельные координатным осям, и три вращательных движения относительно этих осей), которые осуществляются одновременно и независимо друг от друга.

Таким образом, свободное тело в пространстве имеет шесть степеней свободы.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид
В теоретической механике движение свободного тела в пространстве рассматривают как сложное, состоящее из поступательного движения со скоростью некоторой точки тела, принятой за полюс, и сферического движения вокруг этого полюса (рис. 2.60).

Примем произвольную точку О за полюс и поместим в него начала двух подвижных систем отсчёта OXYZ, O2X2Y2Z2. При этом система отсчёта OXYZ неподвижно закреплена на теле, а система отсчёта O2X2Y2Z2 совершает поступательное движение таким образом, что её координатные оси параллельны координатным осям неподвижной системы отсчёта O1X1Y1Z1.

Плоскости OXY, O2X2Y2 подвижных систем отсчёта пересекаются по линии OL. Введением единичного вектора р эту линию преобразуют в ось узлов.

На рис. 2.60 показаны углы Ψ, φ, θ, величины которых зависят от времени. Эти углы называют эйлеровыми углами.

Таким образом, свободное движение тела определяется шестью уравнениями движения свободного твёрдого тела.

Первые три уравнения, определяющие поступательную часть движения тела, зависят от выбора полюса О, так как координаты различных точек тела различны.

Остальные три уравнения, определяющее сферическое движение тела вокруг полюса, от выбора полюса не зависят.

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

В технических расчётах движение свободного тела рассматривают также как вращательное движение относительно мгновенной оси вращения, проходящей через подвижный полюс (рис. 2.61).

Скорость VM любой точки М свободного тела равна геометрической сумме скорости VO полюса О и скорости VMO этой точки в её сферическом движении вокруг полюса.

Скорость VMO определяют по формуле

где Ω – вектор мгновенной угловой скорости; rM – радиус-вектор, начало которого находится в полюсе, а конец в точке М.

Для студентов заочной и дистанционной форм обучения выполнение курсовых заданий на свободное движение тела не предусмотрено.

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Урок 7. Механическое движение. Основные определения кинематики.

ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Видео:Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | Инфоурок

Дифференциальные уравнения относительного движения материальной точки

В предыдущих главах исходили из основного закона классической механики (второго закона Ньютона), который справедлив для движения по отношению к инерциальным системам отсчета. Напомним, что инерциальной («неподвижной») является такая система отсчета, по отношению к которой выполняется закон инерции. Во многих случаях необходимо исследовать движение точки по отношению к неинерциальной системе отсчета, например, по отношению к какому-либо движущемуся объекту (кораблю, автомобилю и т. д.).

Пусть материальная точка М под действием системы сил F]y F2, . Fn движется относительно системы отсчета Oxyz, которая, в

свою очередь, движется относительно инерциальной системы отсчета («неподвижных осей») OxxxyxZ-

Для решения задач динамики относительного движения материальной точки, т. е. движения материальной точки по отношению к неинерциальным, произвольно движущимся системам отсчета, необходимо найти зависимость между относительным ускорением точки аг и действующими на нее силами.

Для абсолютного движения (по отношению к «неподвижной» системе отсчета OxxxyxZ) основной закон динамики имеет вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Из кинематики известно, что абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного аг, переносного ае и кориолисова ак, т. е. а -аг +ае + ак. Подставив это значение а в равенство (15.1) и оставив в левой части уравнения таг, получим

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Векторные величины Фе и Фк (численно равные произведениям тае и так и направленные противоположно ускорениям ае и ак) называют соответственно переносной и кориолисовой силами инерции.

Тогда уравнение (15.2) примет вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Уравнение (15.4) представляет собой основное уравнение динамики для относительного движения материальной точки. Сравнивая равенства (15.1) и (15.4), заключаем, что уравнения движения материальной точки в неинерциальной системе координат составляются аналогично уравнениям абсолютного движения, но при этом к действующим на точку силам добавляются переносная и кориолисова силы инерции. Добавление сил Фе и Фк (не являющихся физическими силами, т. е. воздействиями на точку других тел) отражает кинематику движения подвижной системы отсчета Oxyz по отношению к инерциальной («неподвижной») системе отсчета OxxxyxZ-

Действительно, равенство (15.2) можно представить в виде:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

В правой части этого равенства первое слагаемое выражает ускорение, которое точке сообщают действующие силы Fk, а два других слагаемых являются ускорениями, которые точка имеет вследствие движения подвижной системы отсчета. Все ускорения правой части этого равенства определяются относительно инерциальной («неподвижной») системы отсчета, а результат, т. е. аг, будет определен по отношению к подвижной системе отсчета.

Заметим, что действующие на точку силы Fk сообщают ей ускорение, равное Z Fk/m, в любой системе координат; но по отношению к инерциальной системе отсчета это будет всей величиной ускорения точки, а по отношению к неинерциальной системе отсчета — только его частью.

Рассмотрим некоторые частные случаи.

1. Пусть подвижные оси по отношению к «неподвижным» осям движутся поступательно. В этом случае угловая скорость вращения подвижных осей Oxyz будет со = 0, отсюда Фк = -2т(й>х Vr ) = 0, и закон относительного движения (15.4) принимает вид:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Отметим также, что при поступательном движении подвижной системы отсчета переносные силы инерции для всех материальных точек переносного пространства будут одинаковы, т. е. не будут зависеть от положения, занимаемого точкой в подвижной системе отсчета.

2. Пусть подвижные оси перемещаются по отношению к «неподвижным» поступательно, равномерно и прямолинейно. При таком движении осей Oxyz имеем кинематические характеристики: со = 0, а х =0, а» =0. Так как со = 0, то Фк =0, а из второго и третьего равенств получим, что ае = 0 и, следовательно, Фе =0. Тогда равенство (15.4) принимает вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Сопоставляя равенства (15.5) и (15.1), видим, что в рассматриваемом случае дифференциальное уравнение относительного движения материальной точки совпадает с дифференциальным уравнением ее движения по отношению к неподвижным осям. Из полученного результата следует, что никаким механическим экспериментом нельзя обнаружить, находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение по отношению к «неподвижной» системе отсчета. В этом и состоит открытый Галилеем (1638) принцип относительности классической механики.

По отношению к такой движущейся системе отсчета, как и по отношению к неподвижной, при условии Y,Fk =0 будет выполняться закон инерции. Поэтому все системы отсчета, движущиеся поступательно, равномерно и прямолинейно, а также покоящиеся, называются инерциальными. Заметим, что совпадение дифференциальных уравнений движений по отношению к «неподвижным» и подвижным осям не означает одинаковости самих движений. Ведь законы движения точки в каждой системе отсчета будут получены путем интегрирования дифференциальных уравнений. Постоянные интегрирования в уравнениях движения по отношению к разным системам отсчета будут различны, так как начальные скорости точки (являющиеся начальными условиями) по отношению к каждой системе отсчета (у которых имеется взаимное движение) будут различными.

3. Состояние относительного покоя. В этом случае по отношению к подвижным осям точка имеет такие кинематические характеристики: аг = 0 и Vr =0 и, следовательно, Фк = -2m(coxVr) =0. Тогда равенство (15.4) принимает вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Это уравнение является уравнением относительного равновесия (покоя) точки. Заметим, что при относительном покое к точке должны быть приложены такие внешние силы, которые бы «компенсировали» переносное движение, т. е. чтобы разность ускорений Y,Fk/m-ae была равна нулю.

Задача 15.1. Определить период малых колебаний в вертикальной плоскости математического маятника (масса материальной точки т, невесомая нерастяжимая нить маятника длиной /), точка О подвеса которого движется вверх по вертикали с ускорением w (рис. 15.1).

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Решение. Рассмотрим движение материальной точки как сложное, считая движение ползуна О и связанной с ним системы отсчета Оху (движется поступательно вверх с ускорением w) переносным, а движение маятника по дуге окружности радиусом ОМ= I — относительным движением по отношению к подвижной системе отсчета Оху. Длину дуги ОхМ обозначим через 5.

Так как переносное движение является поступательным (следовательно, , то после подстановки выражений для величин уравнение (б) примет вид:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Ограничимся рассмотрением малых колебаний маятника, считая угол

Ф малым и полагая приближенно sin ф — ф. Тогда, обозначив к = (g+ w)/l, предыдущее уравнение примет вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением (14.2) свободных прямолинейных колебаний точки, и, пользуясь результатами, полученными при его решении, определим период качания маятника:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Задача 15.2. Горизонтальная трубка ЛВ вращается вокруг вертикальной оси Z (рис. 15.2, а) с постоянной угловой скоростью со = 2 с» 1 . Внутри трубки находится шарик М массой т — 1 кг, который к точке А прикреплен пружиной; коэффициент жесткости пружины с — 8 Н/м, длина пружины в ненапряженном состоянии / = 0,5 м. В начальный момент времени /0 = 0 шарик находился в точке М0 на расстоянии АМ0 — s0 = 1,2 м и имел скорость относительно трубки VQ — 1,6 м/с, направленную от оси вращения. Определить закон движения шарика по трубке; в момент времени tx — л/2 с найти силу давления шарика на стенку трубки и силу упругости пружины.

Решение. 1. Рассмотрим движение шарика М как сложное, считая его движение вдоль трубки относительным, а вращение трубки и связанной с ней подвижной системы отсчета Oxyz — переносным движением. Начало координат О подвижной системы отсчета совместим с трубкой в точке расположения незакрепленного конца недеформированной пружины (т. е. АО — /), а ось у направим вдоль трубки от оси вращения.

Рассмотрим шарик в произвольном положении М, при котором пружина растянута, а направления векторов Vr и аг совпадают с направлением оси у (рис. 15.2, б). Hji шарик действуют сила тяжести Р, сила_упруго- сти F и реакция трубки N, которую представим составляющими Nx и Nz.

Для составления уравнения относительного движения шарика присоединим к этим силам переносную силу инерции Фе =-тае и кориолисову силу

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

инерции Фк—так; так как вращение трубки равномерное (со = const), то ае=а» и сила Фе направлена от оси вращения (эту силу называют еще центробежной силой инерции).

Уравнение относительного движения в векторной форме будет иметь вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Чтобы получить дифференциальное уравнение движения точки М по трубке, спроецируем равенство (а) на ось Оу:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

В нашем случае Фе — та п е — т& 2 (1 + у); F—cy. Подставив эти выражения в уравнение (б), представим его в виде

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Решение неоднородного дифференциального уравнения (в) ищем как сумму общего решения (14.3) соответствующего однородного уравнения и частного решения неоднородного уравнения, т. е. у — у + _у2> где yj = = С, cos kt + С2 sin kt и у2 = D/k 2 .

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Найдем еще закон изменения скорости Vr = у:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

По начальным условиям при t0 = 0 у0 = 1,6 м/с, yQ = s0 — I = 0,7 м, которым должны удовлетворять функции (г) и (д), найдем С <= 0,2 м, С2 = = 0,8 м. Вычислим D/k 2 — 0,5 м. В результате общее решение (г) примет окончательный вид, м:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Это уравнение и определяет искомый закон относительного движения шарика по трубке, из которого видно, что это будет колебательное движение с круговой частотой к — 2 с -1 .

2. Рассмотрим воздействия на движущийся шарик в момент времени — л/2 с.

Сила упругости пружины F будет F, = су<, где ух = 0,2 cos л + 0,8 sin л + + 0,5 = 0,3 м. Тогда находим F, = 8 ? 0,3 = 2,4 Н.

Определим реакцию трубки. Для этого спроецируем векторное равенство (а) на оси Ох и Oz:

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Кориолисова сила инерции Фк = таК — т2ыу. Из равенства (д), подставив значения С, = 0,2, С2 = 0,8 и tx = л/2 с, определим ух = —1,6 м/с. Тогда при tx — л/2 с получим Фк = 1 • 2 • 2 • (—1,6) =^6,4 Н. Знаки величин ух и Фк указывают, что реальные векторы ^ и Фк в момент времени = л/2 с будут противоположны показанным на рис. 15.2.

Подставив в равенства (е), (ж) значения Фк и P=mg, находим Nxj = —6,4 кН, Nz| = 9,81 Н. Реакция трубки при tx = л/2 с будет

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Давление шарика на трубку в момент^времени tx будет численно равно Nx и направлено противоположно силе Nx.

Видео:Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1

Кинематика точки

Так как изучение движения всякого тела приводится к изучению движения всех его точек, то вообще механика должна быть начинаема с изучения различных обстоятельств движения точки.

Основы, на которых строится кинематика, дают аксиомы геометрии. Никаких дополнительных законов или аксиом для кинематического изучения движения не требуется. Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано). Кинематически задать движение или закон движения тела (точки) — значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Установление математических способов задания движения точек или тел является одной из важных задач кинематики. Поэтому изучение движения любого объекта начинается с установления способов задания этого движения. Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.

Движущая точка описывает в пространстве некоторую линию. Эта линия, представляет собой геометрическое место последовательных положений движущейся точки, в рассматриваемой системе отсчета, называется траекторией точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Изучение движения точки заключается в определении основных характеристик этого движения: положения точки в выбранной системе отсчета, ее скорости и ускорения в любой момент времени.

Существует три способа задания движения точки: естественный, векторный и координатный.

  • • Естественный способописания движения точки требует задания ее траекторииотносительно выбранной системы отсчета Oxyz . На траектории следует указать началоM0 и положительное направлениеотсчета расстояний
  • s = M0M,

где s — расстояние от начала отсчета M0 до точки M, измеренное вдоль дуги траектории и взятое с соответствующим знаком. Положению M0 необходимо поставить в соответствие начальный момент времени t0 , например t0 = 0 .

Движение точки будет определено, если для каждого момента времени t > t0 будет известна величина s, указывающая положение точки на ее траектории, т.е. если будет задана зависимость s = f(t) . Данное равенство называется законом движения или уравнением движения точки. По самой природе движения функция f(t) должна быть: однозначной, поскольку в один и тот же момент времени движущаяся точка не может находиться в двух различных точках пространства; непрерывной, поскольку движение непрерывно и каждому бесконечно малому изменению t соответствует бесконечно малое изменение s ; дифференцируемой, т.е. должна допускать производную. Если s = const на промежутке времени Дt , то это означает, что точка на этом промежутке времени относительно данной системы отсчета находится в покое.

· Координатный способ описания движения точки состоит в том, что задаются: какая-либо система координат, связанная с телом отсчета; координаты движущейся точки, как функции времени. Чаще всего для определения положения точки используется прямоугольная декартовая система координат Oxyz .

В декартовой системе движение точки задается в виде x = x(t), y = y(t), z = z(t). Каждое из указанных уравнений, взятое отдельно, определяет закон движения проекции точки на соответствующую ось, а все вместе — позволяют в каждый момент времени t определить положение точки M по отношению к системе Oxyz . Данные уравнения также являются параметрическими уравнениями траектории точки, в которых параметром является время t . В случае плоского движения, т.е. когда траектория точки есть плоская кривая, закон движения точки относительно какой-либо системы координат, расположенной в плоскости движения, выразится только двумя уравнениями. Например, когда точка движется в плоскости Oxy , законами движения могут быть:

Исключая время t в последних системах уравнений, получим уравнения траектории плоского движения в декартовых координатах F(x,y) = 0 или полярных координатах Ц(r, ц) = 0 .

· Векторный способ описания движения точки основан на задании ее положения при помощи радиус-вектора r, проведенного из начала O выбранной системы ориентировки Oxyz к движущейся точке M .

Очевидно, что при движении точки M в пространстве ее радиус-вектор r будет изменяться с течением времени как по направлению, так и по величине. Следовательно, в векторной форме закон движения точки представим в виде

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют видДвижение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

Траекторией точки M при векторном способе описании движения будет годограф радиус-вектора . В частности, векторным законом движения точки на координатной плоскости Oxy будет

Движение точки м происходит относительно системы отсчета oxyz уравнения движения точки имеют вид

В зависимости от вида траектории точки ее движение может быть прямолинейным или криволинейным, причем свойства траектории зависят от выбора системы отсчета. Так движение, прямолинейное относительно одной системы отсчета, может быть криволинейным относительно другой, и наоборот.

🔥 Видео

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.

Cложное движение точки. ТермехСкачать

Cложное движение точки. Термех

Как построить точки в системе координат OXYZСкачать

Как построить точки в системе координат OXYZ

Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать

Материальная точка. Система отсчета | Физика 9 класс #1 | Инфоурок

Физика - уравнения равноускоренного движенияСкачать

Физика - уравнения равноускоренного движения

Уравнение движенияСкачать

Уравнение движения

Механическое движение. 9 класс.Скачать

Механическое движение. 9 класс.

Относительность движения | Физика 9 класс #9 | ИнфоурокСкачать

Относительность движения | Физика 9 класс #9 | Инфоурок

Видеоурок по физике "Механическое движение. Системы отсчёта"Скачать

Видеоурок по физике "Механическое движение. Системы отсчёта"

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Равномерное движение точки по окружности | Физика 10 класс #7 | Инфоурок

Кинематика точки Задание К1Скачать

Кинематика точки Задание К1

Способы описания движения Система отсчётаСкачать

Способы описания движения Система отсчёта

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорение

Вращательное движение. 10 класс.Скачать

Вращательное движение. 10 класс.

Термех. Кинематика. Сложное движение точкиСкачать

Термех. Кинематика. Сложное движение точки
Поделиться или сохранить к себе: