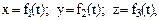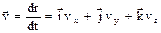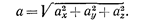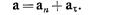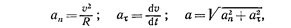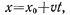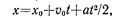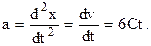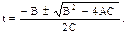Движение материальной точки задано уравнением x at bt2 ct3 где (5 видео)

Содержание

Момент времени, координата и ускорение, когда скорость равна нулю (14 мая 2010)
Комментарии
Движение материальной точки задано уравнением x=At+Bt², где A =4 м/с, В=-0,05 м/с². Определить момент времени, в который скорость v точки
Ваш ответ
решение вопроса
Похожие вопросы
Схема решения задач по кинематике
💡 Видео

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Момент времени, координата и ускорение, когда скорость равна нулю (14 мая 2010)

Методичка была взята в библиотеке университета. Задания на контрольные работы № 1 «Физические основы механики» и № 2 «Молекулярная физика. Основы термодинамики», 1 курс, вариант № 1. Северо-Западный государственный заочный технический университет, Санкт-Петербург, 2006 год. Задача № 102.

версия для печати
Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Видео:Задача на движение материальной точки - bezbotvyСкачать

Движение материальной точки задано уравнением x=At+Bt², где A =4 м/с, В=-0,05 м/с². Определить момент времени, в который скорость v точки

Видео:Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Ваш ответ

Видео:Урок 1. Кинематика прямолинейного движения материальной точки.Скачать

решение вопроса

Видео:Физика - уравнения равноускоренного движенияСкачать

Схема решения задач по кинематике

Записав условие задачи, сделать рисунок, на котором указать систему координат, изобразить траекторию движения точки. Отметить на рисунке кинематические характеристики движения: перемещение, скорость, ускорение. Если указывается, что на отдельных участках движение имеет различный характер, то необходимо рассматривать движение на каждом из них отдельно.

Установить связь между величинами, отмеченными на рисунке. Поскольку для решения системы уравнений и расчетов используется скалярная форма уравнений, то необходимо спроецировать входящие в уравнения векторы на оси выбранной системы координат. Полученную систему уравнений дополнить уравнениями, составленными на основе вспомогательных условий задачи и, проверив равенство количества уравнений и количества неизвестных, входящих в нее, решить систему кинематических уравнений относительно искомых величин.

Практическое занятие 1.

Теория

Положение материальной точки в пространстве задается радиусом-векторомг:

где i, j, k — единичные векторы направлений (орты); х, у, z — координаты точки.

Кинематические уравнения движения в координатной форме:

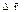
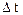
где— перемещение материальной точки за интервал времени.

Средняя путевая * скорость

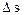
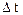
где — путь, пройденный точкой за интервал времени .

где — проекции скорости v на оси координат.

• Ускорение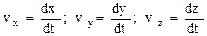

где проекции ускорения a на оси

Движение материальной точки задано уравнением x at bt2 ct3 где

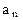
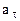
При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих (рис.1.1):

Модули этих ускорений:

где R — радиус кривизны в данной точке траектории.

• Кинематическое уравнение равномерного движения материальной точки вдоль оси х

где 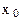— начальная координата; t — время. При равномерном движении

• Кинематическое уравнение равнопеременного движения( 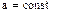)вдоль оси x

где v₀ —начальная скорость; t— время.

Скорость точки при равнопеременном движении

Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct 3 , где A=4 м, B=2 м/с, С=-0,5 м/с 2 . Для момента времени t₁=2 с определить:

1) координату x₁ точки, 2) мгновенную скорость v₁, 3) мгновенное ускорение a₁.

Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t₁:

Подставим в это выражение значения A, В, С, t₁ и произведем вычисления:

2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени: .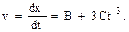

Тогда в заданный момент времени t₁ мгновенная скорость

v₁=B+3Ct₁ 2 Подставим сюда значения В, С, t₁ и произведем вычисления:

Знак минус указывает на то, что в момент времени t₁=2 с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:

Мгновенное ускорение в заданный момент времени t₁ равно a₁=6Ct₁. Подставим значения С, t₁и произведем вычисления:

Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

Пример 2. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид, x=A+Bt+Ct 2 , где A=5 м, B=4 м/с, С=-1 м/с 2 . Построить график зависимости координаты х и пути s от времени. 2. Определить среднюю скорость за интервал времени от t₁=1 с до t₂=6 с. 3. Найти среднюю путевую скорость за тот же интервал времени.

Решение. 1. Для построения графика зависимости координаты точки от времени найдем характерные значения координаты — начальное и максимальное и моменты времени, соответствующие указанным координатам и координате, равной нулю.

Начальная координата соответствует моменту t=0. Ее значение равно

Максимального значения координата достигает в тот момент, когда точка начинает двигаться обратно (скорость меняет знак). Этот момент времени найдем, приравняв нулю первую производную от координаты повремени:

, откуда t=—B/2C=2 с Максимальная координата

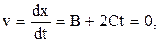
Момент времени t, когда координата х=0, найдем из выражения x=A+Bt+Ct 2 =0.

Решим полученное квадратное уравнение относительно t:

Подставим значения А, В, С и произведем вычисления:

Таким образом, получаем два значения времени: t’-=5 с и 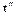=-1 с. Второе значение времени отбрасываем, так как оно не удовлетворяет условию задачи (t>0).

График зависимости координаты точки от времени представляет собой кривую второго порядка. Для его построения необходимо иметь пять точек, так как уравнение кривой второго порядка содержит пять коэффициентов. Поэтому кроме трех вычисленных ранее характерных значений координаты найдем еще два значения координаты, соответствующие моментам t₁=l с и t₂=6 с:

Полученные данные представим в виде таблицы:

Время, с Координата, м

t₁=0 x₀=A=5

t₁=1 x₀=8

t_B=2 x_max=9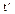

=5 x=0

t₂=6 x₂=-7

Используя данные таблицы, чертим график зависимости координаты от времени (рис. 1.2).

График пути построим, исходя из следующих соображений:

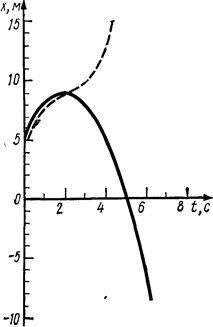1) путь и координата до момента изменения знака скорости совпадают; 2) начиная с момента возврата (t_B) точки она движется в обратном направлении и, следовательно, координата ее убывает, а путь продолжает возрастать по тому же закону, по которому убывает координата.

Следовательно, график пути до момента времени t_B =2 с совпадает с графиком координаты, а начиная с этого момента является зеркальным отображением графика координаты.

2. Средняя скорость за интервал времени t₂—t₁ определяется выражением

Подставим значения x₁, x₂, t₁, t₂. из таблицы и произведем вычисления

3. Среднюю путевую скорость находим из выражения

где s — путь, пройденный точкой за интервал времени t₂.—t₁. Из графика на рис. 1.2 видно, что этот путь складывается из двух отрезков пути: S₁=x_max—x₁, который точка прошла за интервал времени t_B—t₁, и S₂=x_max+|x₂|, который она прошла за интервал

Подставим в это выражение значения x_max , |x₂|, x₁ и произведем вычисления :

Тогда искомая средняя путевая скорость

Заметим, что средняя путевая скорость всегда положительна.

Задачи

1.1. Две прямые дороги пересекаются под углом 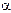=60°. От перекрестка по ним удаляются машины: одна со скоростью v₁=60 км/ч, другая со скоростью v₂=80 км/ч.

Определить скорости v’ и v», с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно.

1.2. Точка двигалась в течение t₁=15c со скоростью v₁=5 м/с, в течение t₂=10 с со скоростью v₂=8 м/с и в течение t₃=6 с со скоростью v₃=20 м/с. Определить среднюю путевую скорость точки.

1.3. Три четверти своего пути автомобиль прошел со скоростью v₁=60 км/ч, остальную часть пути — со скоростью v₂=80 км/ч. Какова средняя путевая скорость автомобиля?

1.4. Первую половину пути тело двигалось со скоростью v₁=2 м/с, вторую — со скоростью v₂=8 м/с. Определить среднюю путевую скорость .

1.5. Тело прошло первую половину пути за время t₁=2 с, вторую — за время t₂=8 с. Определить среднюю путевую скорость тела, если длина пути s=20 м.

1.6. -Зависимость скорости от времени для движения некоторого тела представлена на рис. 1.4. Определить среднюю путевую скорость за время t=14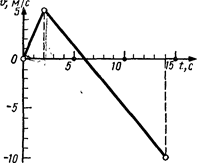

1.7. Зависимость ускорения от времени при некотором движении тела представлена на рис. 1.5. Определить среднюю путевую скорость за время t=8 с. Начальная скорость v₀=0.

1.8. Уравнение прямолинейного движения имеет вид x=At+Bt 2 , где A=3 м/с, B=—0,25 м/с 2 . Построить графики зависимости координаты и пути от времени для заданного движения.

1.9. На рис. 1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.

1.10. Движение материальной точки задано уравнением x=At+Bt 2 , где A =4 м/с, В=—0,05 м/с 2 . Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

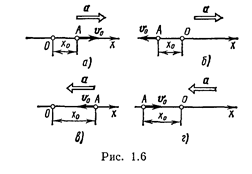
1.11. Написать кинематическое уравнение движения x=f(t) точки для четырех случаев, представленных на рис. 1.6. На каждой позиции рисунка — а, б, в, г — изображена координатная ось Ох, указаны начальные положение x₀ и скорость v₀ материальной точки А, а также ее ускорение а.

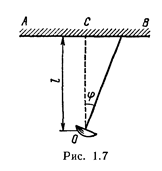
1.12. Прожектор О (рис. 1.7) установлен на расстоянии l==100 м от стены АВ и бросает светлое пятно на эту стену. Прожектор вращается вокруг вертикальной оси, делая один оборот за время Т=20 с. Найти: 1) уравнение движения светлого пятна по стене в течение первой четверти оборота; 2) скорость v, с которой светлое пятно движется по стене, в момент времени t=2 с. За начало отсчета принять момент, когда направление луча совпадает с ОС.

1.13. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а=0,1 м/с 2 , человек начал идти в том же направлении со скоростью v=1,5 м/с. Через какое время t поезд догонит человека? Определить скорость v₁ поезда в этот момент и путь, пройденный за это время человеком.

1.14. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью v₁==l м/с и ускорением a₁=2 м/с 2 , вторая — с начальной скоростью v₂=10 м/с и ускорением а₂=1 м/с 2 . Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

1.15. Движения двух материальных точек выражаются уравнениями:

В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v₁ и v₂ и ускорения a₁ и а₂ точек в этот момент:

1.16. Две материальные точки движутся согласно уравнениям;

В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v₁ и v₂ точек в этот момент.

1.17. С какой высоты Н упало тело, если последний метр своего пути оно прошло за время t=0,1 с?

1.18. Камень падает с высоты h=1200 м. Какой путь s пройдет камень за последнюю секунду своего падения?

1.19. Камень брошен вертикально вверх с начальной скоростью v₀==20 м/с. По истечении какого времени камень будет находиться на высоте h=15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g=10 м/с 2 .

1.20. Вертикально вверх с начальной скоростью v₀=20 м/с брошен камень. Через 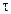=1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте h встретятся камни?

1.21. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h=8,6 м два раза с интервалом 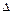t=3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

1.22. С балкона бросили мячик вертикально вверх с начальной скоростью v₀=5 м/с. Через t=2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.

1.23. Тело брошено с балкона вертикально вверх со скоростью v₀=10 м/с. Высота балкона над поверхностью земли h=12,5 м. Написать уравнение движения и определить среднюю путевую скорость с момента бросания до момента падения на землю.

1.24. Движение точки по прямой задано уравнением x=At+Bt 2 , где A =2 м/с, В=—0,5 м/с 2 . Определить среднюю путевую скорость движения точки в интервале времени от t₁=l с до t₂=3 с.

1.25. Точка движется по прямой согласно уравнению x=At+Bt 3 , где A=6 м/с, В == —0,125 м/с 3 . Определить среднюю путевую скорость точки в интервале времени от t₁=2 с до t₂=6 с.