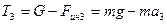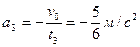Про уравнения - легко » Статьи

Движение груза а задано уравнением y at 2 bt c решение

Обновлено
Содержание
  1. Определение параметров движения твердого тела
  2. Методичні рекомендації для підготовки до зимової заліково-екзаменаційної сесії, для студентів заочної форми навчання факультету транспортних технологій та економіки спеціальності «ОПУВТ» (стр. 2 )
  3. Определение параметров движения твердого тела
  4. 💡 Видео

Видео:Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать

Первая основная задача динамики. Задачи 1, 2, 3, 4

Определение параметров движения твердого тела

Задание

Движение груза А задано уравнением y = at Движение груза а задано уравнением y at 2 bt c решение+ bt + c, где [y] = м, [t] = c.

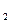
Цель работы – подставив заданные коэффициенты в общее уравнение движения, определить вид движения. Определить скорость и ускорение груза в моменты времени t Движение груза а задано уравнением y at 2 bt c решениеи t Движение груза а задано уравнением y at 2 bt c решение, а также скорость и ускорение точки В на ободе барабана лебедки (рис.3.3 и табл.3.1).

Теоретическое обоснование

Точки тела движутся по окружностям вокруг неподвижной оси (ось вращения).

Закон равномерного вращательного движения: φ = φ Движение груза а задано уравнением y at 2 bt c решение+ wt. (3.1)

Закон равнопеременного вращательного движения: φ = φ Движение груза а задано уравнением y at 2 bt c решение+ w Движение груза а задано уравнением y at 2 bt c решениеt + Движение груза а задано уравнением y at 2 bt c решение(3.2)

Закон неравномерного вращательного движения: φ = f(t 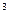Движение груза а задано уравнением y at 2 bt c решение).

Здесь φ – угол поворота тела за время t , рад;

w – угловая скорость, рад/с;

φ Движение груза а задано уравнением y at 2 bt c решение— угол поворота, на который развернулось тело до начала отсчета;

w Движение груза а задано уравнением y at 2 bt c решение— начальная угловая скорость;

ε — угловое ускорение, рад/с Движение груза а задано уравнением y at 2 bt c решение

Угловая скорость: w = Движение груза а задано уравнением y at 2 bt c решение; w = w Движение груза а задано уравнением y at 2 bt c решение+ εt; (3.3)

Угловое ускорение: ε = Движение груза а задано уравнением y at 2 bt c решение.

Кинематические графики вращательного движения представлены на рис. 3.1а, б.

Движение груза а задано уравнением y at 2 bt c решение

А б

Рис.3.1

Число оборотов вращения тела: z = φ(2π).

Угловая скорость вращения: n, об/мин.

w = 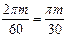Движение груза а задано уравнением y at 2 bt c решение(3.4)

Движение груза а задано уравнением y at 2 bt c решениеРис.3.2

Параметры движения точки вращающегося тела (рис.3.2):

v – линейная скорость точки В

a Движение груза а задано уравнением y at 2 bt c решение— касательное ускорение точки В

a Движение груза а задано уравнением y at 2 bt c решение= εr, м/с Движение груза а задано уравнением y at 2 bt c решение(3.6)

а Движение груза а задано уравнением y at 2 bt c решение— нормальное ускорение точки В

а Движение груза а задано уравнением y at 2 bt c решение= w Движение груза а задано уравнением y at 2 bt c решениеr, м/с Движение груза а задано уравнением y at 2 bt c решение(3.7)

Порядок выполнения работы

1. Определить вид движения, подставив заданные коэффициенты в общее уравнение движения.

2. Определить уравнения скорости и ускорения груза.

3. Определить полное число оборотов шкива.

4. Определить нормальное и касательное ускорения точки на ободе шкива в указанные моменты времени.

5. Ответить на контрольные вопросы.

Контрольные вопросы

1. В чем заключается принцип кинетостатики?

2. Могут ли при поступательном движении тела траектории его точек не прямыми линиями?

3. Равна ли скорость перемещения груза скоростям точек на ободе вращающегося шкива?

4. Как повлияет на скорость груза увеличение диаметра шкива при неизменной угловой скорости?

5. Какое ускорение (касательное или нормальное) характерно для точек вращающегося тела?

Пример выполнения

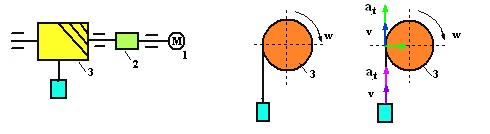
Для перемещения груза применена барабанная лебедка, привод которой состоит из электродвигателя 1 и редуктора 2 (понижает угловую скорость вала двигателя до требуемой на барабане). Барабан 3 служит для преобразования вращательного движения в поступательное движение груза. Диаметр барабана d = 0,2 м, а уравнение его вращения φ = 30t + 6t Движение груза а задано уравнением y at 2 bt c решение. Для момента времени t Движение груза а задано уравнением y at 2 bt c решение= 0,5 с, определить все кинематические характеристики движения барабана, точки на его ободе, а также груза. Направление движения груза – вверх.

Движение груза а задано уравнением y at 2 bt c решение

1. Определяем кинематические характеристики движения барабана. Угол поворота барабана за время t Движение груза а задано уравнением y at 2 bt c решениеφ1 = 30*0,5 + 6*0,5 Движение груза а задано уравнением y at 2 bt c решение= 16,5 рад.

Угловая скорость барабана w = Движение груза а задано уравнением y at 2 bt c решение= (30t + 6t Движение груза а задано уравнением y at 2 bt c решение)´ = 30 + 12t ≠ const – движение неравномерное. При t Движение груза а задано уравнением y at 2 bt c решение= 0,5 с получим w Движение груза а задано уравнением y at 2 bt c решение= 30 + 12*0,5 = 36 рад/с

Угловое ускорение барабана ε = Движение груза а задано уравнением y at 2 bt c решение= (30 + 12t)´ = 12 рад/с Движение груза а задано уравнением y at 2 bt c решение= const. Так как ускорение положительно и постоянно, то барабан вращается равноускоренно.

2. Кинематические характеристики движения любой точки на ободе барабана, например точки

А , определяются через угловые характеристики движения барабана.

Для момента времени t Движение груза а задано уравнением y at 2 bt c решениеполучим: расстояние, пройденное точкой s = φ Движение груза а задано уравнением y at 2 bt c решениеr = 16,5 *0,1 = 1,65 м

Скорость точки v Движение груза а задано уравнением y at 2 bt c решение= w Движение груза а задано уравнением y at 2 bt c решение*r = 36*0,1 = 3,6 м/с; касательное ускорение a Движение груза а задано уравнением y at 2 bt c решение= εr = 12*0,1 = 1,2 м/с Движение груза а задано уравнением y at 2 bt c решение; нормальное ускорение а Движение груза а задано уравнением y at 2 bt c решение= w Движение груза а задано уравнением y at 2 bt c решениеr = 36 Движение груза а задано уравнением y at 2 bt c решение*0,1 = 130 м/с Движение груза а задано уравнением y at 2 bt c решение.

3. Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки А, лежащей на ободе барабана.

Литература: Движение груза а задано уравнением y at 2 bt c решение

Таблица 3.1

ВариантПараметр
а, м/с Движение груза а задано уравнением y at 2 bt c решение.в, м/сс, мr, мt 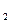Движение груза а задано уравнением y at 2 bt c решение, мt Движение груза а задано уравнением y at 2 bt c решение, м
0,2
0,4
0,6
0,8
0,5
0,4
0,3
0,2
0,8
0,6
0,2
0,4
0,6
0,8
0,5
0,4
0,3
0,2
0,8
0,6
0,2
0,4
0,6
0,8
0,5
0,4
0,3
0,2
0,8
0,6

Движение груза а задано уравнением y at 2 bt c решениеРис. 3.3

Практическая работа № 4

Работа и мощность. Общие теоремы динамики

Задания

Скорость кабины лифта массой m изменяется согласно графикам (рис.4.4). Используя принцип Даламбера определить натяжение каната кабины лифта на каждом участке движения. Определить максимальное натяжение каната. По максимальному натяжению каната определить максимальную потребную мощность для подъема груза. По заданной величине КПД механизма определить максимальную мощность двигателя (табл. 4.1).

Движение груза а задано уравнением y at 2 bt c решение

Цель работы– научиться рассчитывать мощность с учетом потерь на трение и сил инерции,определять параметры движения с помощью теорем динамики

Теоретическое обоснование

Принципом Даламбера называют метод, позволяющий решать задачи динамики приемами статики.Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы». Работа служит мерой действия силы, работа – скалярная величина.

Работа постоянной силы. Работа постоянной по модулю и направлению силы при прямолинейном перемещении определяется скалярным произведением вектора силы на вектор перемещения точки ее приложения.

A = F S cos ( Движение груза а задано уравнением y at 2 bt c решение) = F S cosα (4.1)

Работа силы трения: AFтр = Fтр S cos ( Движение груза а задано уравнением y at 2 bt c решение) = fтр NS cos180 = — fтрNS (4.2)

Работа силы, приложенной к вращающемуся твердому телу: А = Движение груза а задано уравнением y at 2 bt c решение= A = Mz φ. (4.3)

Для характеристики работоспособности и быстроты совершения работы введено понятие мощности

Мощность при поступательном движении

P=Fυ cos α (4.4)

где F- постоянная сила, H; υ – скорость движения, м/с; α- угол между направлениями силы и перемещения.

Мощность при вращение

P=Mω, (4.5)

где М – вращающий момент, Н*м; ω – угловая скорость, рад/с.

Коэффициент полезного действия

где Рпол – полезная мощность, Вт; Рзатр – затраченная мощность, Вт.

где а – ускорение точки, м/с; m – масса, кг.

Основные уравнения динамики

Поступательное движение твёрдого тела: F = ma/

Вращательное движение твёрдого тела: Mz = τε

где Mz — суммарный момент внешних сил относительно оси вращения, кг*м;

ε – угловое ускорение, рад/с.

Порядок выполнения работы

1. Используя принцип Даламбера определить натяжение каната кабины лифта на каждом участке движения.

2. Определить максимальное натяжение каната.

3. По максимальному натяжению каната определить максимальную потребную мощность для подъема груза.

4. По заданной величине КПД механизма определить максимальную мощность двигателя.

5. Ответить на контрольные вопросы.

Контрольные вопросы

  1. Какие силы называют движущими?
  2. Какие силы называют силами сопротивления?
  3. Запишите формулы для определения работы при поступательном и вращательном движениях?
  4. Можно ли задачи динамики решать с помощью уравнений равновесия?
  5. Чему равна работа силы тяжести при горизонтальном перемещении тела?
  6. Как изменится кинетическая энергия прямолинейно движущейся точки, если ее скорость увеличится в два раза?

Пример выполнения

График изменения скорости лифта при подъеме известен (рис.4.1). Масса лифта с грузом

2800 кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема.

  1. Рассмотрим участок 1 – подъем с ускорением. Составим схему сил (рис.4.2). Уравнение равновесия кабины лифта:

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Где Т – натяжение каната;

G – сила тяжести;

F Движение груза а задано уравнением y at 2 bt c решение— сила инерции, растягивающая канат.

Для определения ускорения на участке 1 учтем, что движение на этом участке равнопеременное, скорость Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Движение груза а задано уравнением y at 2 bt c решение

Определяем усилие натяжения каната при подъеме с ускорением

2800(9,81 + 1,25) = 30968 Н; Т Движение груза а задано уравнением y at 2 bt c решение= 30,97 кН

  1. Рассмотрим участок 2 – равномерный подъем. Ускорение и сила инерции равны нулю. Натяжение каната равно силе тяжести.

Т Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение; Движение груза а задано уравнением y at 2 bt c решение

  1. Участок 3 – подъем с замедлением. Ускорение направлено в сторону, обратную направлению подъема. Составим схему сил (рис.4.3)

Уравнение равновесия: Движение груза а задано уравнением y at 2 bt c решение, отсюда Движение груза а задано уравнением y at 2 bt c решение

Ускорение (замедление) на этом участке определяется с учетом того, что v = 0.

Движение груза а задано уравнением y at 2 bt c решение; Движение груза а задано уравнением y at 2 bt c решение

Натяжение каната при замедлении до остановки:

Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Таким образом, натяжение каната меняется при каждом подъеме и опускании, канат выходит из строя в результате усталости материала. Работоспособность зависит от времени.

Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Рис.4.1 Рис.4.2 Рис.4.3

Рис. 4.4

1 Движение груза а задано уравнением y at 2 bt c решение2 Движение груза а задано уравнением y at 2 bt c решение3 Движение груза а задано уравнением y at 2 bt c решение
4 Движение груза а задано уравнением y at 2 bt c решение5 Движение груза а задано уравнением y at 2 bt c решение6 Движение груза а задано уравнением y at 2 bt c решение
7 Движение груза а задано уравнением y at 2 bt c решение8 Движение груза а задано уравнением y at 2 bt c решение9 Движение груза а задано уравнением y at 2 bt c решение
10 Движение груза а задано уравнением y at 2 bt c решение

Таблица 4.1

ВариантПараметр
Масса, кгКПД механизмаРисунок
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75
0,80
0,85
0,70
0,75

Практическая работа № 5

Движение груза а задано уравнением y at 2 bt c решение

Последнее изменение этой страницы: 2017-03-17; Просмотров: 3659; Нарушение авторского права страницы

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Уравнение движения тела дано в виде x=2−3t. Вычисли

Методичні рекомендації для підготовки до зимової заліково-екзаменаційної сесії, для студентів заочної форми навчання факультету транспортних технологій та економіки спеціальності «ОПУВТ» (стр. 2 )

Движение груза а задано уравнением y at 2 bt c решениеИз за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8

Движение груза а задано уравнением y at 2 bt c решение

пластины. Толщина пластинки постоянная.

Движение груза а задано уравнением y at 2 bt c решение

Центр тяжести однородной тонкой пластинки
постоянной толщины, имеющей очертание плоской фигуры, называется центром тяжести площади данной плоской фигуры и его координаты находят по формулам:

Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение,

k — число простейших геометрических фигур, на которые возможно

условно разбить заданную фигуру;

Движение груза а задано уравнением y at 2 bt c решение— площадь k— ой простейшей фигуры;

Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение— координаты центра тяжести k— ой простейшей фигуры;

Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение— координаты центра тяжести всей фигуры;

Движение груза а задано уравнением y at 2 bt c решение— площадь всей фигуры.

Тогда Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.

1. Разобьем нашу пластинку на три простейшие геометрические фигуры:

1. прямоугольник 400Движение груза а задано уравнением y at 2 bt c решение500 мм;

2. полукруг с R = 150 мм;

3. треугольник 270Движение груза а задано уравнением y at 2 bt c решение360 мм,

причем площади двух последних частей будем считать отрицательными.

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

2. Выберем систему координат хОу, как указано на чертеже. Поскольку однородная пластина имеет одинаковую толщину, то можно воспользоваться формулами для определения положения центра тяжести площади.

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Площадь прямоугольника (фигура 1) равна: Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение;

координаты ее центра тяжести Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.

Площадь полукруга (фигура 2) равна:Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение;

координаты ее центра тяжести Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.

Площадь треугольника (фигура 3) равна: Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение,

координаты ее центра тяжести Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.

Движение груза а задано уравнением y at 2 bt c решение=Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Движение груза а задано уравнением y at 2 bt c решение=Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Ответ: координаты центра тяжести Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Задание 3. Движение груза А задано уравнением Движение груза а задано уравнением y at 2 bt c решение,

где [у] = м, [t] = с. Определить скорость и ускорение груза

в моменты времени t1 и t2 , а также скорость и

ускорение точки B на ободе барабана лебедки.

Движение груза а задано уравнением y at 2 bt c решение

Рассмотрим отдельно движение груза и точки B на ободе барабана лебедки.

На рисунке груз совершает поступательное движение вниз. Траектория его движения — прямолинейная. Движение груза А задано уравнением Движение груза а задано уравнением y at 2 bt c решение. Сравним его с уравнением

Движение груза а задано уравнением y at 2 bt c решение,

Это уравнение равнопеременного движения (независимо от его траектории),

где Движение груза а задано уравнением y at 2 bt c решение— путь, пройденный до начала отсчета;

Движение груза а задано уравнением y at 2 bt c решение— начальная скорость движения;

Движение груза а задано уравнением y at 2 bt c решение— постоянное касательное ускорение.

В нашем примере:

Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение= 7м, — начальный путь, пройденный грузом до времени t1 = 1с;

b = Движение груза а задано уравнением y at 2 bt c решение= 6 м/с, — начальная скорость груза;

c = Движение груза а задано уравнением y at 2 bt c решение, — постоянное касательное ускорение.

Ускорение груза А положительно, значит движение равноускоренное и направлено в сторону направления скорости движения груза. Т. к. постоянное касательное ускорение Движение груза а задано уравнением y at 2 bt c решение, то ускорение не зависит от времени.

Уравнение скорости груза можно найти по формуле

Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение, м/с.

Следовательно, скорость груза:

— в моменты времени t1 = 1с: Движение груза а задано уравнением y at 2 bt c решение;

— в моменты времени t2 = 3с: Движение груза а задано уравнением y at 2 bt c решение;

2. Движение точки В на ободе барабана лебедки.

Рассматривая движение точки В на ободе барабана лебедки, учтем, что отдельно взятая материальная точка не вращается, а движется по окружности, т. е. совершает криволинейное движение (вращением называется движение твердого тела, а не точки).

Уравнение равнопеременного криволинейного движения в общем виде:

Движение груза а задано уравнением y at 2 bt c решение,

В нашем примере:

Скорости всех точек троса (он считается нерастяжимым), на котором висит груз, одинаковы. Значит, точки обода имеют такую же скорость.

Касательное ускорение Движение груза а задано уравнением y at 2 bt c решение,

Скорость точки в моменты времени t1 = 1с:

Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение= 16 м/с.

Нормальное ускорение в моменты времени t1 = 1с:

Движение груза а задано уравнением y at 2 bt c решение

Полное ускорение точки В в моменты времени t1 = 1с:

Скорость в моменты времени t1 = 3с:

Нормальное ускорение в моменты времени t1 = 3с:

Движение груза а задано уравнением y at 2 bt c решение

Полное ускорение точки В в моменты времени t1 = 3с:

Ответ: для груза: Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение;

для точки В: Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение,

Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.

Задание 4. На графике показано изменение скорости кабины лифта

массой 2800 кг. Определить величину натяжения каната, на

котором подвешен лифт, при его подъеме и опускании.

По максимальной величине натяжения каната определить

Движение груза а задано уравнением y at 2 bt c решение

Рекомендации по выполнению задания.

1. Параметры движения в конце каждого участка являются начальными

параметрами движения на каждом последующем.

2. Используя принцип Даламбера, определить натяжение каната лифта

на каждом участке движения.

3. Определить максимальное натяжение каната.

4. По максимальному натяжению каната определить потребную мощность

для подъема лифта.

1. Движение груза а задано уравнением y at 2 bt c решениеРассмотрим участок 1 — подъем с ускорением (начало движения с места и с увеличением скорости).

Составим схему сил (см. рис.) и уравнение равновесия кабины лифта. Для этого определим проекции всех сил

на ось у Движение груза а задано уравнением y at 2 bt c решение:

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

где Т — натяжение каната; Движение груза а задано уравнением y at 2 bt c решение— сила тяжести; Движение груза а задано уравнением y at 2 bt c решение— сила инерции, растягивающая канат; Движение груза а задано уравнением y at 2 bt c решение— ускорение на участке 1.

Движение лифта на участке 1 равнопеременное (а именно, равноускоренное), начальная скорость лифта на участке в момент Движение груза а задано уравнением y at 2 bt c решениеравна Движение груза а задано уравнением y at 2 bt c решение.

Скорость на этом участке в любой момент времени Движение груза а задано уравнением y at 2 bt c решениеможно найти из формулы Движение груза а задано уравнением y at 2 bt c решение. Используем ее для нахождения ускорения Движение груза а задано уравнением y at 2 bt c решениев момент времени Движение груза а задано уравнением y at 2 bt c решение, когда Движение груза а задано уравнением y at 2 bt c решение(ускорение Движение груза а задано уравнением y at 2 bt c решениеодинаково с момента Движение груза а задано уравнением y at 2 bt c решениедо Движение груза а задано уравнением y at 2 bt c решение):

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Определим усилие натяжения каната при подъеме с ускорением:

Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение = 2800 (9,81 + 1,25) = 30968 Н = 30,97 кН.

2. Рассмотрим участок 2 — равномерный подъем (подъем с постоянной скоростью без ускорения).

Движение груза а задано уравнением y at 2 bt c решениеУскорение Движение груза а задано уравнением y at 2 bt c решениеи сила инерции Движение груза а задано уравнением y at 2 bt c решениеравны нулю. Тогда скорость движения на участке 2 (в промежутке от Движение груза а задано уравнением y at 2 bt c решениедо Движение груза а задано уравнением y at 2 bt c решение) равна Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Натяжение каната Движение груза а задано уравнением y at 2 bt c решениеравно силе тяжести Движение груза а задано уравнением y at 2 bt c решение: Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение.

Составим схему сил (см. рис.) и уравнение равновесия кабины лифта. Сумма проекций всех сил на ось у равна нулю Движение груза а задано уравнением y at 2 bt c решение:

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение;

Движение груза а задано уравнением y at 2 bt c решениеН Движение груза а задано уравнением y at 2 bt c решениекН.

3. Рассмотрим участок 3 — подъем с замедлением (торможение до полной остановки).
Ускорение Движение груза а задано уравнением y at 2 bt c решение(а точнее, замедление) направлено в сторону, обратную направлению подъема. Составим схему сил и уравнение равновесия. Для этого определим проекции всех сил на ось у Движение груза а задано уравнением y at 2 bt c решение, Движение груза а задано уравнением y at 2 bt c решение.
Отсюда Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение.

Скорость на этом участке находят по формуле Движение груза а задано уравнением y at 2 bt c решение. Используем ее для нахождения ускорения Движение груза а задано уравнением y at 2 bt c решениев момент времени Движение груза а задано уравнением y at 2 bt c решение, когда Движение груза а задано уравнением y at 2 bt c решение(ускорение Движение груза а задано уравнением y at 2 bt c решениеодинаково с момента Движение груза а задано уравнением y at 2 bt c решениедо Движение груза а задано уравнением y at 2 bt c решение):

Движение груза а задано уравнением y at 2 bt c решение или Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеДвижение груза а задано уравнением y at 2 bt c решение.

Натяжение каната от начала замедления до остановки:

Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеН = 25,14 кН.

Как показывает расчет, натяжение каната на всех участках различно. Канат может выйти из строя в результате усталости материала и его работоспособность зависит от продолжительности эксплуатации.

Максимальное натяжение каната — на 1 участке, где Движение груза а задано уравнением y at 2 bt c решение= 30,97 кН.

Полезную мощность электродвигателя лифта можно найти по формуле

Движение груза а задано уравнением y at 2 bt c решение

В нашем примере, т. к. лифт движется вертикально Движение груза а задано уравнением y at 2 bt c решение; движение лифта поступательное.

Тогда Движение груза а задано уравнением y at 2 bt c решениеВт = 154,84 кВт.

Ответ: Движение груза а задано уравнением y at 2 bt c решение= 30,97 кН; Движение груза а задано уравнением y at 2 bt c решениекН; Движение груза а задано уравнением y at 2 bt c решение кН, Движение груза а задано уравнением y at 2 bt c решениекВт.

Задание 5 — выполнить в письменном виде в соответствии с вариантом.

Комп’ютерна техніка і програмування

Питання до іспиту

1. Що означає термін «информатика» і яке його походження?

2. Які сфери людської діяльності і в якому ступені зачіпає інформатика?

3. Назвіть основні складові частини інформатики і основні напрями її вживання.

4. Що мається на увазі під поняттям «информация» в побутовому, природничонауковому і технічному значеннях?

5. Де і як людина береже інформацію?

6. Що необхідно додати в систему «джерело інформації — приймач информации», щоб здійснювати передачу повідомлень?

7. Які типи дій виконує людина з інформацією?

8. Приведіть приклади технічних пристроїв і систем, призначених для збору і обробки інформації.

9. Від чого залежить інформативність повідомлення, що приймається людиною?

10. Чому кількість інформації в повідомленні зручніше оцінювати не по ступені збільшення знання про об’єкт, а по ступеню зменшення невизначеності наших знань про нього?

11. Як визначається одиниця вимірювання кількості інформації?

12. У яких випадках і по якій формулі можна обчислити кількість інформації, що міститься в повідомленні?

13. Чому у формулі Хартлі за підставу логарифма узято число?

14. При якій умові формула Шеннона переходить у формулу Хартлі?

15. Що визначає термін «бит» в теорії інформації і в обчислювальній техніці?

16. Приведіть приклади повідомлень, інформативність яких можна однозначно визначити.

17. Приведіть приклади повідомлень, що містять один (два, три) біт інформації.

18. Яка роль апаратури (Hardware) і програмного забезпечення (Software) комп’ютера?

19. Які основні класи комп’ютерів Вам відомі? В чому полягає принцип дії комп’ютерів?

20. З яких найпростіших елементів складається програма?

21. Що таке система команд комп’ютерів?

22. Перерахуйте головні пристрої комп’ютера.

23. Опишіть функції пам’яті і функції процесора. Назвіть дві основні функції процесора. Яке їх призначення?

24. Що таке регістри? Назвіть деякі важливі регістри і опишіть їх функції.

25. Сформулюйте загальні принципи побудови комп’ютерів.

26. У чому полягає принцип програмного управління? Як виконуються команди умовних і безумовних переходів?

27. У чому суть принципу однорідності пам’яті? Які можливості він надає?

28. У чому полягає принцип адресності?

29. Яка архітектура називається «фон-неймановскими»?

30. Що таке команда? Що описує команда?

31. Якого роду інформацію може містити адресна частина команди?

32. Приведіть приклади команд одноадресних, двоадресних, триадресних.

33. Яким чином процесор при виконанні програми здійснює вибір чергової команди?

34. Опишіть основний цикл процесу обробки команд.

35. Що розуміється під архітектурою комп’ютера? Які характеристики комп’ютера визначаються цим поняттям? Чи вірно, що спільність архітектури різних комп’ютерів забезпечує їх сумісність в плані реалізації функціональних елементів?

36. Що розуміється під структурою комп’ютера? Який рівень деталізації опису комп’ютера може вона забезпечити?

37. Перерахуйте поширену комп’ютерну архітектуру.

38. Які відмітні особливості класичної архітектури?

39. Чим є шина комп’ютера? Які функції загальної твані (магістралі)?

40. Яку функцію виконують контроллери?

41. Як характер вирішуваних задач пов’язаний з архітектурою комп’ютера?

42. Які відмітні особливості властиві багатопроцесорній архітектурі? Багатомашинній архітектурі? Архітектурі з паралельним процесором?

43. Опишіть роботу стримера.

44. Як працює аудіоадаптер? Відеоадаптер?

45. Які типи відеоплатні використовуються в сучасних комп’ютерах?

46. Назвіть головні компоненти і основних керівників клавіші клавіатури.

47. Перерахуйте основні компоненти відеосистеми комп’ютера.

48. Як формується зображення на екрані кольорового монітора?

49. Які влаштовані рідкокристалічні монітори? Проведіть порівняння таких моніторів з моніторами, побудованими на основі ЗЛТ.

50. Опишіть роботу матричних, лазерних і струменевих принтерів.

51. Ніж робота плоттера відрізняється від роботи принтера?

52. Опишіть спосіб передачі інформації за допомогою модему.

53. Перерахуйте основні види маніпуляторів і опишіть принципи з роботи.

54. Що розуміють під персональним комп’ютером?

55. Які характеристики комп’ютера стандартизуються дня реалізації принципу відкритої архітектури?

56. Що таке апаратний інтерфейс?

57. Яке призначення контроллерів і адаптерів? В чому полягає різниця між контроллером і адаптером?

58. Що таке порти пристроїв? Охарактеризуйте основні види портів.

59. Перерахуйте основні блоки сучасного комп’ютера

60. Яке призначення міжкомп’ютерного зв’язку?

61. Опишіть технологію «клиент-сервер».

62. Яким чином долається проблема несумісності інтерфейсів в комп’ютерних мережах?

63. Що таке протокол комунікації?

64. Чому дані передаються за допомогою пакетів?

65. Охарактеризуйте основні види мережних топології.

66. Назвіть характеристики поширеної мережної архітектури.

67. Дайте коротку характеристику спеціального мережного устаткування.

68. У яких областях і з якою метою застосовуються локальні мережі?

69. Перерахуйте основні сервіси мережі Інтернет.

70. Що таке IP — адреса?

71. Які основні послуги надає користувачам система WWW?

72. Які організовані системи інформаційного пошуку мережі Інтернет?

73. Дайте порівняльну характеристику систем інформаційного пошуку Yahoo! і Alta Vista.

74. У якій послідовності виникали відомі Вам мови програмування?

75. Коли мікрокомп’ютери стали доступні для широкого домашнього вживання?

76. Чи можете Ви зв’язати поняття «яблоко» «гараж» і «компьютер»?

77. На основі яких технічних елементів створювалися комп’ютери першого покоління?

78. Яку основну проблему перед розробниками і користувачами висунув досвід експлуатації комп’ютерів першого покоління?

79. Яка елементна база характерна для іншого покоління комп’ютерів?

80. Яку функцію виконує операційна система в процесі роботи комп’ютера?

81. На якій елементній базі конструюються машини третього покоління?

82. З яких основних етапів складається процес виготовлення мікросхем?

83. Для яких поколінь комп’ютерів характерне широке використовування інтегральних схем?

84. Яка швидкодія характерна для машин четвертого покоління?

85. Що мають на увазі під «інтеллектуальністью» комп’ютерів?

86. Яку задачу повинен вирішувати «інтеллектуальний интерфейс» в машинах п’ятого покоління?

87. Якими особливостями повинні володіти промислові комп’ютери?

88. Що таке операторський комп’ютерний інтерфейс?

89. По яких основних ознаках можна відрізнити мейнфрейми від інших сучасних комп’ютерів?

90. На яку кількість користувачів розраховані мейнфрейми?

91. Які ідеї лежать в основі архітектури суперкомп’ютерів?

92. На яких типах задач максимально реалізуються можливості суперкомп’ютерів?

93. Які властивості і конструктивні особливості відрізняють векторні процесори?

94. Назвіть основні характеристики якого-небудь суперкомп’ютера.

95. Що означають в перекладі на російську мову назви Laptop, Notebook, Palmtop?

96. Як в Palmtop компенсується відсутність накопичувачів на дисках?

97. Одиниці вимірювання інформації. Організація даних на диску.

98. Логічні основи побудови ПК. Основи алгебри логіки.

99. Функціонально-структурна організація ГЖ. Основні блоки ПК та їх призначення.

100. Центральний мікропроцесор, його призначення. Основні характери­ стики мікропроцесорів.

101. Запам’ятовуючі пристрої ПК та їх порівняльні характеристики.

102. Базова система введення-виведення (BIOS). Функції BIOS.

103. ОС MS-DOS. Основні команда.

104. ОС Windows 98, Windows 2000 та Windows XP. Основні характери­ стики. Переваги та недоліки.

105. Об’єкти файлової системи — файл і папка: правила створення імен, пе­ регляд властивостей.

106. Настройка робочого середовища ОС Windows.

107. Управління ресурсами комп’ютера за допомогою програми Провідник: перегляд дисків, виділення, створення, вилучення, копіювання, переміщення, перейменування об’єктів.

108. Програма-оболонка Norton Commander. Основні операції з об’єктами файлової системи,

109. Архівація даних. Алгоритми кодування інформації та коефіцієнт стиснення.

110. Програми-архіватори. Створення та обробка архівів.

111. Характеристика та класифікація комп’ютерних вірусів. Антивірусні програмні засоби.

112. Програми обслуговування магнітних дисків.

113. Робота з текстовим процесором Microsoft Word: копіювання, переміщення і видалення тексту; форматування символів, абзаців, сторінок; робота з вікнами.

114. Робота з текстовим процесором Microsoft Word: пошук та заміна фрагментів тексту; закладки, перехресні і гіперпосшіання; списки та стилі; колонтитули; вкладені документи; створення змісту; злиття документів; робота з редактором формул.

115. Сервісні функції текстового процесора Microsoft Word: перевірка пра­ вопису, розміщення переносів, додавання автоматичних назв до таблиць, формул та малюнків, створення панелей користувачів, додавання кнопок на панель інструментів, завдання комбінацій гарячих клавіш, запис макросів.

116. Робота з табличним процесором Microsoft Excel: основні поняття і можливості; абсолютні та відносні посилання в формулах; автоматичне за­ повнення комірок.

117. Робота з табличним процесором Microsoft Excel: сортування даних;

118. зв язок комірок, аркушів, книг; створення диаграм.

119. Створення форм в табличному процесорі Microsoft Excel за допомогою елементів управління.

120. Системи керування базою даних. Файл-серверна та клієнт-серверна архітектури: відмінності, переваги та недоліки.

121. Реляційний підхід до побудови бази даних. Нормалізація відношень. Типи зв’язків.

122. Робота з програмою Microsoft Access: створення таблиць і зв’язків між ними, введення даних; властивості підстановок; пошук, сортування, фільтрація даних; створення і застосування запитів.

123. Комп’ютерні мережі й телекомунікації. Загальне поняття про компьютеры! мережі. Класифікація комп’ютерних мереж.

124. Світова глобальна комп’ютерна мережа Internet. Принципи функціонування глобальної мережі. Інтегрований браузер Internet Explorer. Гіпертекст. Принципи використання Web-сторінок

Комп. техніка і програмування

1. Бройдо системы, сети и телекоммуникации. Учебник для вузов. — СПб.: Питер, 2003,688 с.

2. 5 Цибулин в математическом исследовании. Учебный курс. — СПб.: Питер, 2001, 624 с.

3. Гук интерфейсы ПК. Энциклопедия. — СПб.: Питер, 2003,528 с.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Физика - перемещение, скорость и ускорение. Графики движения.

Определение параметров движения твердого тела

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ИРКУТСКИЙ ЭНЕРГЕТИЧЕСКИЙ КОЛЛЕДЖ

РАСЧЕТНО-ГРАФИЧЕСКаяРАБОТа

ПО ПРЕДМЕТУ

«ТЕХНИЧЕСКАЯ МЕХАНИКА»

ВАРИАНТ 10

Выполнил: студент гр. 2РЗ1

Работа №
Оценка

ИРКУТСК 2011

Практическая работа № 1

Определение равнодействующей плоской системы сходящихся сил

Задания:

Заданы модули сил F1, F2, F3, пересекающихся в одной точке, и направление этих сил – углы α1, α2, α3 относительно оси Х (рис. 1.1 и табл. 1.1) .

Цель работы – произвести графическое и аналитическое исследование плоской системы сходящихся сил, выявить уравновешена ли заданная система сил.

F1 = 7 Н, α = 150 Движение груза а задано уравнением y at 2 bt c решение, F2 = 8Н, α2 = 45 Движение груза а задано уравнением y at 2 bt c решение, F3 = 9H, α3 = 330 Движение груза а задано уравнением y at 2 bt c решение

Графическое определение равнодействующей.

Выбираем масштаб сил – μF = 1Н/ см

Модуль равнодействующей — Движение груза а задано уравнением y at 2 bt c решение= μF * 1 = 0.1*87,4 = 8,74

Направление равнодействующей — Движение груза а задано уравнением y at 2 bt c решение= 32,20°

Движение груза а задано уравнением y at 2 bt c решение

2. Аналитическое определение равнодействующей проекции заданных сил на оси х и у:

Модуль равнодействующей: F∑ Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение= Движение груза а задано уравнением y at 2 bt c решение= 8.733968 H;

Направление равнодействующей: α 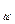Движение груза а задано уравнением y at 2 bt c решение= arctg Движение груза а задано уравнением y at 2 bt c решение

Относительные погрешности

Погрешность вычисления модуля равнодействующей.

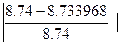
Движение груза а задано уравнением y at 2 bt c решение* 100% = Движение груза а задано уравнением y at 2 bt c решение* 100% = 0,069%

Погрешность вычисления направления равнодействующей

Движение груза а задано уравнением y at 2 bt c решение*100% = Движение груза а задано уравнением y at 2 bt c решение*100% = -0,071%

Вывод: система является неуравновешенной.

Модуль равнодействующей — F∑ Движение груза а задано уравнением y at 2 bt c решение = 8,74 Н, направление — Движение груза а задано уравнением y at 2 bt c решение= 32,222°.

Относительные погрешности не превышают 5%.

Вывод 2: Погрешность программы, по которой был начерчен чертёж

не превышает 0,2% (скорее всего программа просто округлила значения до десятых долей)

Контрольные вопросы №1

1. Графическое сложение плоской системы сходящихся сил производят построением силового многоугольника.Порядок сложения векторов т.е НЕ F1 к F2 к F3 и т.д , а например F3 к F1 к F5 Сильно влияет на величину равнодействующей.

2. Равнодействующая направлена из начала координат к концу последнего вектора.

3. Да. Если конец вектора последней силы совпал с началом вектора первой силы, то система уравновешена.

5. Если модуль равнодействующей равен нулю, то система уравновешена.

4.Она определяется умножением силы на угол Движение груза а задано уравнением y at 2 bt c решение. Проекция равна нулю если: 1) проекция ведётся на ось х и угол равен 90 т.е cos90=0. 2)П проекция ведётся на ось у и угол равен 180 т.е sin180=0.

6. Графический способ определения равнодействующей следует применять, если сил мало и для наглядного изображения, а аналитический для точного расчёта.

7. Чтоб произвести уравновешивание плоской системы сходящихся сил надо наверное вычислить равнодействующую и заменить её век

Практическая работа № 2

Расчётные схемы балок и определение реакции их опор

Задание

Задана горизонтальная двух опорная балка. Балка нагружена активными силами: сосредоточенной F, распределенной силой интенсивностью q и парой сил с моментом М (табл.2.1 и рис 2.6).

Цель работы – построить расчётную схему балки, составить уравнения равновесия балки, определить реакции ее опор и выявить наиболее нагруженную опору.

Дано:

q = 4 H/м, F = 50 H, M = 10 H*м, α = 120°

Преобразование заданных сил:

Fx = F cos α = 50cos 120° = -25, Fy = F sinα = 50 sin120° = 43.3012

Составим расчётную схему

Движение груза а задано уравнением y at 2 bt c решение

Движение груза а задано уравнением y at 2 bt c решение
Движение груза а задано уравнением y at 2 bt c решение
Движение груза а задано уравнением y at 2 bt c решение
Движение груза а задано уравнением y at 2 bt c решение

Движение груза а задано уравнением y at 2 bt c решение Движение груза а задано уравнением y at 2 bt c решениеА В С D

Уравнения равновесия и определение реакций опор:

Движение груза а задано уравнением y at 2 bt c решениеа) ∑Mia = 0; -Q *AB/2 – Fy * AC+ RB * 3 – M = 0;

RB = Движение груза а задано уравнением y at 2 bt c решение

RAy = Движение груза а задано уравнением y at 2 bt c решение

Наиболее нагруженной является опора В – RB =-40.3Н. Нагрузка на опору А – RA = Движение груза а задано уравнением y at 2 bt c решение

Контрольные вопросы №2

1.Сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил?

Для плоской системы параллельных сил составляется два независимых уравнения равновесия. Для плоской системы произвольно расположенных сил-три(исключая проверочное уравнение).

2.Какие составляющие реакции опор балок возникают в шарнирно – подвижной, шарнирно – неподвижной опорах и жёсткой заделке?

В шарнирно – подвижной опоре балки возникает реакция, направленная вверх перпендикулярно опорной плоскости. В шарнирно-неподвижной опоре – реакция направлена перпендикулярно оси шарнира, такую реакцию разлагают на две взаимно-перпендикулярные составляющие. В жёсткой заделки возникает реактивная сила с реактивным моментом. Реактивную силу разлагают на две взаимно-перпендикулярные составляющие.

3.Какую точку целесообразно выбрать в качестве центра момента при определении реакций опор?

Точку приложения силы.

4.Какая система является статически неопределимой?

Конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции.

Практическая работа № 3

Определение параметров движения твердого тела

Задание

Движение груза А задано уравнением y = at Движение груза а задано уравнением y at 2 bt c решение+ bt + c, где [y] = м, [t] = c.

Цель работы – подставив заданные коэффициенты в общее уравнение движения, определить вид движения. Определить скорость и ускорение груза в моменты времени t Движение груза а задано уравнением y at 2 bt c решениеи t Движение груза а задано уравнением y at 2 bt c решение, а также скорость и ускорение точки В на ободе барабана лебедки.

Движение груза а задано уравнением y at 2 bt c решение

Дано: a = 2м/с Движение груза а задано уравнением y at 2 bt c решение, b = 0 м/с, с = 0 м, r = 0,8м, t1 = 3c, t2 = 5 c.

1. Определяем кинематические характеристики движения барабана. Угол поворота барабана за время t Движение груза а задано уравнением y at 2 bt c решениеy = 0*4 + 2*2 + 3= 7 рад.

Угловая скорость барабана w = y´ = (at Движение груза а задано уравнением y at 2 bt c решение+ bt + c)´ = 4* t + 0 ≠ const – движение неравномерное. При t Движение груза а задано уравнением y at 2 bt c решение= 3 с получим w Движение груза а задано уравнением y at 2 bt c решение= 2 * 3 + 3 = 9 рад/с

Угловое ускорение барабана ε = a´= (2t + 0)´ = 2 рад/с Движение груза а задано уравнением y at 2 bt c решение= const. Так как ускорение положительно и постоянно, то барабан вращается равноускоренно.

2. Кинематические характеристики движения любой точки на ободе барабана, например точки

B, определяются через угловые характеристики движения барабана.

Для момента времени t Движение груза а задано уравнением y at 2 bt c решениеполучим: расстояние, пройденное точкой s = y*r = 7* 0.6 = 4.2м

Скорость точки v Движение груза а задано уравнением y at 2 bt c решение= w Движение груза а задано уравнением y at 2 bt c решение*r = 9 * 0,6 = 5,4 м/с; касательное ускорение a Движение груза а задано уравнением y at 2 bt c решение= εr = 2*0,6 = 1,2 м/с Движение груза а задано уравнением y at 2 bt c решение; нормальное ускорение а Движение груза а задано уравнением y at 2 bt c решение= w Движение груза а задано уравнением y at 2 bt c решениеr = 9 Движение груза а задано уравнением y at 2 bt c решение*0,6 = 48,6 м/с Движение груза а задано уравнением y at 2 bt c решение.

3. Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки B, лежащей на ободе барабана.

Контрольные вопросы №3

1. В чем заключается принцип кинетостатики?

Принцип кинетостатики заключается в том, что уравнения движения записываются в форме уравнений равновесия, т.к силы инерции вместе с активными и реактивными силами.

2. Могут ли при поступательном движении тела траектории его точек не прямыми линиями?

При поступательном движении тела траектории его точек могут быть и не прямыми линиями.

3. Равна ли скорость перемещения груза скоростям точек на ободе вращающегося шкива?

Скорость перемещения груза является равной линией скорости движения точек шкива.

4. Как повлияет на скорость груза увеличение диаметра шкива при неизменной угловой скорости?

При увеличение диаметра шкива и неизменной узловой скорости, скорость груза увеличивается.

5. Какое ускорение (касательное или нормальное) характерно для точек вращающегося тела?

Для любой точки, вращающегося тела, характерно и нормальное и касательное ускорение, за исключением равномерного вращения, для которого характерно только нормальное ускорение, касательное в этом случае равно нулю.

💡 Видео

Задачи на движение двух объектовСкачать

Задачи на движение двух объектов

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 класс

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.

Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Вращательное движение твёрдого тела. Задачи 1, 2, 3

Уравнение движенияСкачать

Уравнение движения

Вращательное движение. 10 класс.Скачать

Вращательное движение. 10 класс.

ЕГЭ Задание 11 Задача на движение Система уравненийСкачать

ЕГЭ Задание 11 Задача на движение Система уравнений

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 класс

Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Урок 37. Движение тела, брошенного под углом к горизонту (начало)

Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnline

Относительность механического движения. Практическая часть - решение задачи. 7 класс.Скачать

Относительность механического движения. Практическая часть - решение задачи. 7 класс.

Уравнение Лагранжа 2-го рода. Линейная координатаСкачать

Уравнение Лагранжа 2-го рода. Линейная координата

ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать

ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.

Решение задач по теме Законы НьютонаСкачать

Решение задач по теме Законы Ньютона

Уравнение равномерного движения. Решение задач по теме.Скачать

Уравнение равномерного движения. Решение задач по теме.

Урок 315. Решение задач динамикиСкачать

Урок 315. Решение задач динамики

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Урок 93. Основное уравнение динамики вращательного движения
Поделиться или сохранить к себе: