Две стороны треугольника заданы уравнениями 5x 2y 8 0

Стороны треугольника заданы уравнениями:

Найти координаты вершин треугольника.

Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:

Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем

Вершина A имеет координаты

Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:

получаем .

Координаты вершины C получим, решая систему из уравнений сторон BC и AC:

Вершина C имеет координаты .

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Аналитическая геометрия Индивидуальные задания и методические указания по выполнению модуля (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Две стороны треугольника заданы уравнениями 2x + y – 1 = 0 и x – 3y + 14 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны

Даны уравнения сторон треугольника: (АВ) 7x – 2y + 32 = 0; (АС) x + y + 2 = 0; (ВС) 4x + y + 1 = 0. Найти точку пересечения его высот

Составьте уравнения катетов прямоугольного равнобедренного треугольника, если уравнение гипотенузы 3x – y + 11 = 0 и С(4;3) – вершина прямого угла

В равнобедренном треугольнике известны: уравнение основания 5x + 3y – 53 = 0, уравнение одной из боковых сторон x + 4y – 14 = 0 и точка на второй боковой стороне (3;7). Найдите уравнение второй боковой стороны

Одна из сторон квадрата лежит на прямой x – 5y + 32 = 0, а одна из вершин находится в точке (8;1). Найдите уравнения остальных сторон квадрата

Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4x – 7y + 28 = 0, концы которого лежат на осях координат

Точки К(1;3) и L(-1;1) являются серединами оснований равнобедренной трапеции, а точки Р(3;0) и Q(-3;5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции

Даны стороны треугольника: (АС) 2x – 15y – 55 = 0; (AB) 4x – 3y + 25 = 0; (BC) 14x + 3y – 61 = 0. Составить уравнение прямой, проходящей через вершину С и через точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4

Точки В(7;1) и D(9; -3) являются противоположными вершинами квадрата. Определить координаты двух других вершин

В треугольнике известны уравнения высоты x + y – 3 = 0 и медианы 11x – 4y + 10 = 0, проведенных из различных вершин. Написать уравнения сторон треугольника, зная одну его вершину (8;9).

Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты 11x – 9y + 75 = 0 и биссектрисы 11x – 13y + 79 = 0, проведенных из одной вершины

Точка А(2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой x + y – 1 =0. Составить уравнения двух других сторон

Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в точке М(1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба

Точка А(1;2) является серединой одного из оснований прямоугольной трапеции, а точка В(3; -1) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x – 3y + 10 = 0. Составить уравнения остальных сторон трапеции

Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы x + y – 5 =0 и медианы x – y = 0, проведенных из различных вершин

Даны координаты двух вершин треугольника А(-1;3), В(2;5) и ортоцентр – точка Н(1;4). Найти координаты третьей вершины треугольника. (Ортоцентром треугольника называется точка пересечения его высот)

Точка Н(-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2x – y = 0 и x + y – 3 =0. Составить уравнение третьей стороны

Найти радиус и координаты центра окружности, проходящей через точку А(-1;3) и касающейся прямых 7x + y = 0 и x – y + 8 = 0

Окружность проходит через точки М(1;0) и N(2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5x – y – 4 = 0

Точки В(1;2) и С(3; -6) симметричны относительно некоторой прямой. Составить уравнение этой прямой

Диагонали параллелограмма пересекаются в точке К(-2;4). Составить уравнение диагонали, не проходящую через точку пересечения сторон 4x – y + 4 = 0 и 4x +3y +20 = 0

Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку А (-4;8)

Составить уравнение прямой L1, параллельной прямой L2: 2x + 3y – 23 = 0, если середина отрезка прямой L3: 5x +2y +3 = 0, заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 5x – y + 24 = 0

Составить уравнение стороны треугольника, в котором известны точка пересечения медиан (-1;7) и уравнения двух других сторон x + 4y – 37 = 0; 2x – y + 16 = 0

Даны две стороны x – y + 5 = 0 и x – y + 10 = 0 и диагональ 3x + y – 10 = 0 ромба. Найти вершины ромба

В треугольнике известны две вершины А(-2;9), В(2; -3) и точка пересечения высот О(2;7). Написать уравнения сторон

Точка А(3; -2) является вершиной квадрата, а точка М(1;1) – точкой пересечения его диагоналей. Составить уравнения сторон квадрата

Даны уравнения одной из сторон ромба x + y – 39 = 0 и одной из его диагоналей x – 3y + 11 = 0. Найти уравнения остальных сторон ромба

Найти координаты вершин параллелограмма, в котором известны две стороны 2x – 5y – 5 = 0 и 2x + 5y – 15 = 0 и диагональ 6x + 5y – 35 = 0

Найти координаты точек С и D четырехугольника ABCD, в котором отрезки АВ и DC параллельны, BD и АС перпендикулярны друг другу и заданы вершины А(9; -1), В(5;5)

Даны две вершины (3; -1), (1;4) и центр тяжести (0;2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон

Даны уравнения двух высот треугольника 3x + 4y – 23 = 0 и 12x – 5y – 24 = 0 и одна из его вершин (1;1). Составить уравнения сторон

Написать уравнения сторон треугольника, две медианы которого лежат на прямых x + y – 3 = 0 и 2x + 3y – 1 = 0, а точка А(1;1) является вершиной треугольника

Две стороны треугольника заданы уравнениями, x + 3y – 21 = 0 и 7x + y + 13 = 0, а середина третьей стороны – точка (2;3). Составить уравнение третьей стороны

Даны уравнения сторон треугольника: (MN) 3x – 5y + 17 = 0, (NP) 8x + 6y – 32 = 0, (МР) 5x + 11y + 9 = 0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот)

Гипотенуза прямоугольного треугольника лежит на прямой 2x + y – 2 = 0, а точка С(3; -1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты

Основание равнобедренного треугольника лежит на прямой x + 2y – 2 = 0, а одна из боковых сторон – на прямой y + 2x – 1 =0. Составить уравнение другой боковой стороны треугольника, зная, что ее расстояние от точки пересечения данных прямых равно

Составить уравнения сторон квадрата, в котором одна из вершин – точка (8;7) и одна из сторон лежит на прямой 5x + 2y + 4 = 0

Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2x + y – 8 = 0, концы которого лежат на окружности (х – 3)2 + y2 = 4

Точки М(3;7) и N(2;3) являются серединами оснований равнобедренной трапеции. Точки К(1;7) и Р(4;6,5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции

Даны стороны треугольника: (АВ) 4x + 3y – 10 = 0; (ВС) 3x + 2y – 8 = 0; (АС) 8x + 5y – 18 = 0. Составить уравнение прямой, проходящей через точку С и делящей сторону АВ в отношении 2:3 (считая от вершины А)

Противоположными вершинами квадрата являются точки

(-5;-3) и (3;17). Найти координаты двух других вершин

Написать уравнения сторон треугольника, зная одну его вершину (2;7), уравнения медианы 9x + y + 4 = 0 и высоты x + 5y – 11 = 0, проведенных из различных вершин

Написать уравнения сторон треугольника, зная одну его вершину (-5;4), уравнения высоты 6x + y – 61 = 0 и биссектрисы 4x – 3y + 7 = 0

Точка М(6;4) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой 3x – y + 2 = 0. Найти уравнения остальных сторон треугольника

Длина стороны ромба с тупым углом 120є равна . Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке (-4;6). Составьте уравнения сторон ромба

Точка Р(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2;3) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x + 3y + 1 = 0. Составить уравнения сторон

Составьте уравнения трех сторон треугольника, в котором медиана 3x + 2y – 6 = 0 и биссектриса x – y = 0 проведены не из вершины (4;0), а из двух других вершин

Даны стороны треугольника: 4x – 3y + 26 = 0(АВ); x + 2y + 1 = 0(АС); 7x + 3y – 37 = 0(ВС). Найти точку пересечения медианы, проведенной из вершины В и высоты, проходящей через вершину С

Найти радиус и координаты центра окружности, проходящей через точку А(-1;8) и касающейся прямых х + 10 = 0 и 4x – 3y + 10 = 0

Точка отстоит на одинаковых расстояниях от точек Р(7;8) и Q(1;2). Найти координаты точки К, если известно, что она лежит на прямой 4x – 5y + 27 = 0

Видео:Уравнения стороны треугольника и медианыСкачать

Задача 41259 Найти уравнение сторон треугольника.

Условие

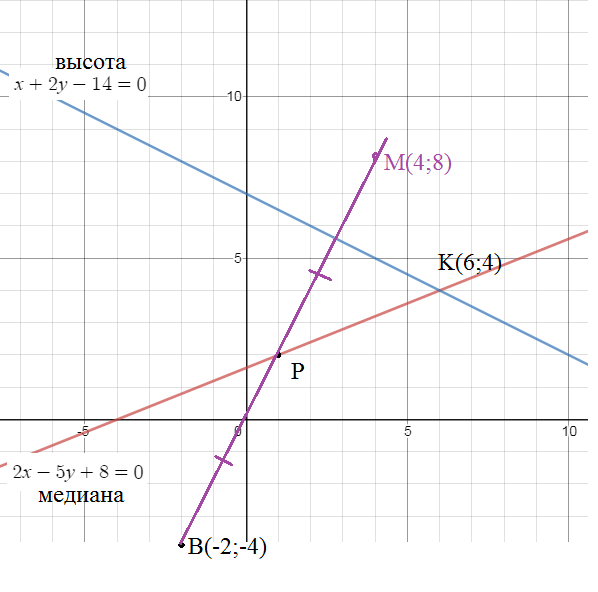
Найти уравнение сторон треугольника, если известны одна из вершин В(-2;-4) и уравнение медианы 2х-5у+8=0 и высоты х+2у-14=0 проведеденных из этой вершины

Все решения

Найдем координаты точки пересечения медианы и высоты:
<2x-5y+8=0
<x+2y-14=0

Назовем ее точка К

Скорее всего дана точка В и два уравнения медианы и высоты,
проведенных из других вершин треугольника

Составим уравнение прямой ВК, как прямой проходящей через две точки:

х+2=y+4
[b]x-y-2=0 [/b]- уравнение ВК

высота x+2y-14=0 и ВК не перпендикулярны,так как произведение угловых коэффициентов взаимно перпендикулярных прямых должно быть равно (-1).

Значит высота перпендикулярна стороне ВМ.

Координату точки М требуется найти

Уравнение стороны ВМ, как прямой, перпендикулярной x+2y-14=0
и проходящей через точку В легко написать.

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент стороны ВМ
k_(BM)=2

Общий вид такой прямой
y=2x+b

Так как ВМ проходит через точку В, подставим ее координаты в уравнение
y=2x+b
и найдем b

уравнение BM: [b]y=2x[/b]

Найдем координаты точки пересечения ВМ и медианы.
Решаем систему уравнений:
<2х–5у+8=0
<y=2x

Пусть это точка Р(1;2)

Уравнение КМ, как уравнение прямой проходящей через две точки:
[m]frac<x-x_><x_-x_>=frac<y-y_><y_-y_>[/m]

[b]2х+у-8=0[/b] — уравнение МК

О т в е т. x-y-2=0; y=2x; 2х+у-8=0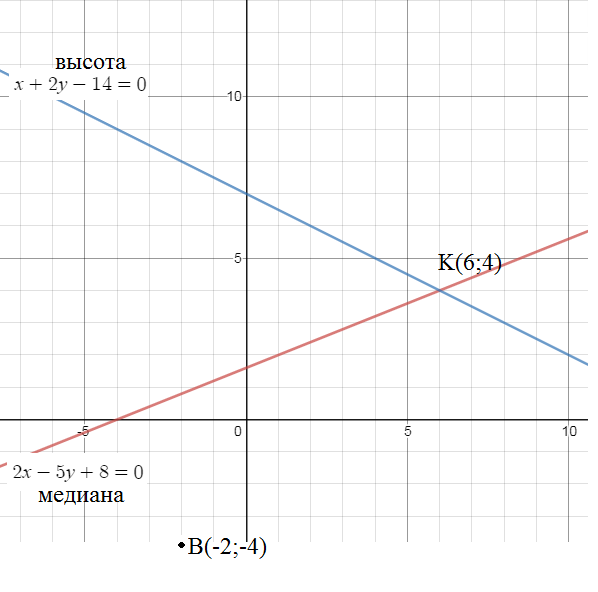

🎦 Видео

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составляем уравнение прямой по точкамСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

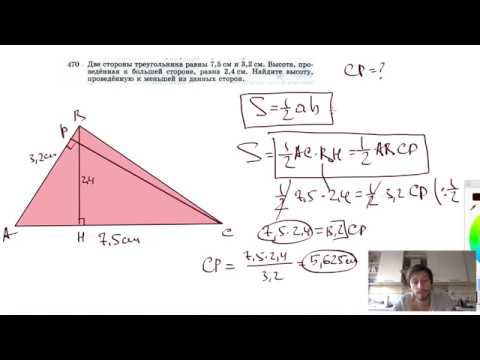
№470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная кСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Задача, которую исключили из экзамена в АмерикеСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Аналитическая геометрия на плоскости. Решение задачСкачать

ОГЭ. Геометрия. 1 часть. Теорема косинусов.Скачать

Уравнение прямой и треугольник. Задача про высотуСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать