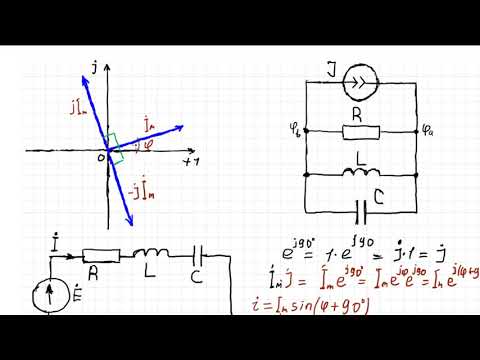
Синусоидальные токи, напряжения. Параметры идеальных элементов электрических цепей синусоидального тока
Общие сведения. Электромагнитный процесс в электрической цепи считается периодическим, если мгновенные значения напряжений и токов повторяются через равные промежутки времени Т. Время Т называется периодом. Напряжения u(t) = u(t+T) и токи i(t)=i(t+T) ветвей электрической цепи являются периодическими функциями времени.
Величина, обратная периоду (число периодов в единицу времени), называется частотой: f = 1/T. Частота имеет размерность 1/c, а единицей измерения частоты служит Герц (Гц).
Широкое применение в электротехнике нашли синусоидальные напряжения и токи:
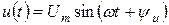
В этих выражениях:
– ω = 2π/T = 2πf – угловая частота (скорость изменения аргумента),
– ωt + ψu, ωt + ψi – фазы, соответственно напряжения и тока.
Графики изменения u(t), i(t) удобно представлять не в функции времени t, а в функции угловой величины ωt , пропорциональной t (рис. 1.1).
Величина φ = (ωt + ψu) – (ωt + ψi) = ψu, — ψi называется углом сдвига фаз. На рис. 1.1 ψu > 0, ψi > 0, φ = ψu — ψi > 0, т.е. напряжение опережает ток. Аналогично можно ввести понятие углов сдвига фаз между двумя напряжениями или токами.
Количество тепла, рассеиваемого на сопротивление R при протекании по нему тока, электромагнитная сила взаимодействия двух проводников с равными токами, пропорциональны квадрату тока. Поэтому о величине тока судят по действующему значению за период. Действующее значение периодического тока i(t) определяется по выражению
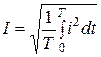
Для квадратов левой и правой частей этого равенства, после умножения их на RT, будем иметь:
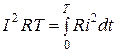
Из этого равенства следует, что действующее значение периодического тока равно по величине такому постоянному току I, который на неизменном сопротивлении R за время T выделяет тоже количество тепла, что и ток i(t).
При синусоидальном токе i(t) = Im sin ωt интеграл
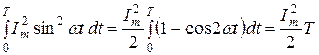
Следовательно, действующее значение синусоидального тока равно
Действующее значение синусоидальных напряжений u(t), э.д.с. e(t) определяются аналогично:
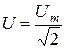
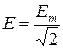
Для измерения действующих значений используются приборы электромагнитной, электродинамической, тепловой и др. систем.
Среднее значение синусоидального тока определяется как среднее за половину периода. Поэтому,
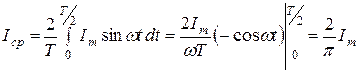
Средние значения синусоидальных напряжений u(t), э.д.с. e(t) определяются аналогично:
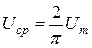
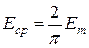
Отношение амплитудного значения к действующему называется коэффициентом амплитуды ka, а отношение действующего значения к среднему – коэффициентом формы kф. Для синусоидальных величин, например, тока i(t), эти коэффициенты равны:
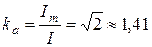
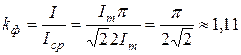
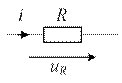
Для синусоидальных токов i(t) = Im sin(ωt + ψi) уравнения идеальных элементов R, L, C при принятых на рис. 1.2. положительных направлениях имеют вид
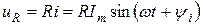
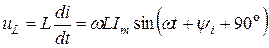
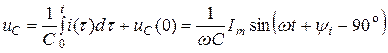
 | 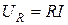 , , 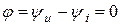 |  |
 | 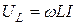 , , 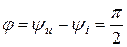 |  |
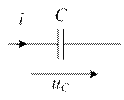 | 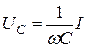 , , 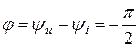 |  |
На активном сопротивлении R мгновенные значения напряжения и тока совпадают по фазе. Угол сдвига фаз φ = 0.
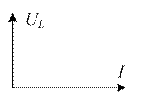
На индуктивности L мгновенное значение тока отстает от мгновенного значения напряжения на угол 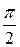
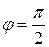
На емкости C мгновенное значение напряжения отстает от мгновенного значения тока на угол 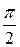
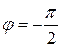
Величины ωL и 1/ωC имеют размерность [Ом] и называются реактивным сопротивлением индуктивности или индуктивным сопротивлением XL:
и реактивным сопротивлением емкости или емкостным сопротивлением XС:
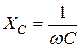
Величины 1/ωL и ωC имеют размерность [Ом -1 ] и называются реактивной проводимостью индуктивности или индуктивной проводимостью BL:
и реактивной проводимостью емкости или емкостной проводимостью BС:
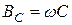
Связь между действующими значениями напряжения и тока на идеальных элементах R, L, C устанавливают уравнения:
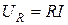
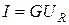
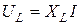
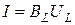
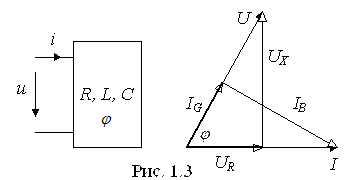
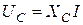
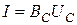
Для синусоидального напряжения u = Um sin ωt начальная фаза тока на входе пассивного двухполюсника (рис. 1.3.) равна
Проекция напряжения на линию тока
называется активной составляющей напряжения.
Проекция напряжения на линию, перпендикулярную току,
называется реактивной составляющей напряжения.
Проекция тока на линию напряжения
называется активной составляющей тока.
Проекция тока на линию, перпендикулярную напряжению,
называется реактивной составляющей тока.
Имеют место очевидные соотношения:
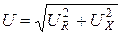
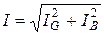
В цепи синусоидального тока для пассивного двухполюсника по определению вводятся следующие величины:
1. Полное сопротивление Z:
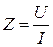
2. Эквивалентные активное Rэк и реактивное Xэк сопротивления:
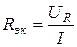
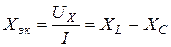
3. Полная проводимость Y:
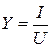
4. Эквивалентные активная Gэк и реактивная Bэк проводимости:

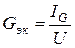
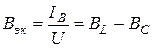
Из треугольников сопротивлений и проводимостей (рис. 1.4) следует:
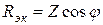
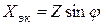
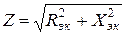
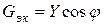
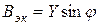
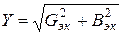
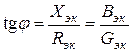
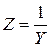
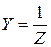
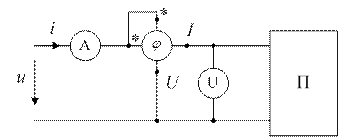
Эквивалентные параметры являются измеряемыми величинами, поэтому могут быть определены из физического эксперимента (рис. 1.5).
Электрическая цепь по схеме рис. 1.5 должна содержать амперметр А и вольтметр U для измерения действующих значений напряжения и тока, фазометр φ для измерения угла сдвига фаз между мгновенными значениями напряжения и тока на входе пассивного двухполюсника П.
Угол сдвига фаз пассивного двухполюсника 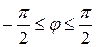
Физическая величина, численно равная среднему значению от произведения мгновенных значений напряжения u(t) и тока i(t), называется активной мощностью Р.По определению имеем:
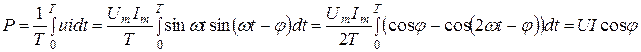
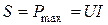
называются полной мощностью S и реактивной мощностью Q в цепи синусоидального тока. Имеет место равенство
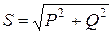
Коэффициент мощности kм в цепи синусоидального тока определяется выражением:

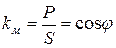
Единицей измерения активной мощности является Ватт [Вт]. Для измерения активной мощности служит ваттметр. Ваттметр включается по схеме рис. 1.6.
Единица измерения полной мощности [ВА], реактивной – [ВАр].
Для вычисления мощностей удобно использовать следующие выражения:
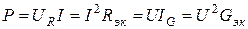
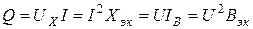
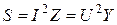
Решение типовых задач. Для измерения мгновенных значений напряжений u(t) и токов i(t) служит осциллограф. Поскольку сопротивление входа этого прибора очень большое, непосредственно для измерения тока осциллограф использовать нельзя. Измеряют не ток, а пропорциональное току напряжение на шунте Rш (рис. 1.7, а).
Задача 1.1. К источнику синусоидального напряжения частотой f = 50 Гц подключена катушка индуктивности (рис. 1.7, а). Активное сопротивление провода, из которого изготовлена катушка, R = 10 Ом, индуктивность L = 1,6 мГн. Осциллограмма напряжения uш(t) представлена на рис. 1.7, б. Сопротивление шунта Rш = 0,1 Ом. Масштаб по вертикальной оси осциллограммы mu = 0,02 В/дел (0,02 вольта на деление).
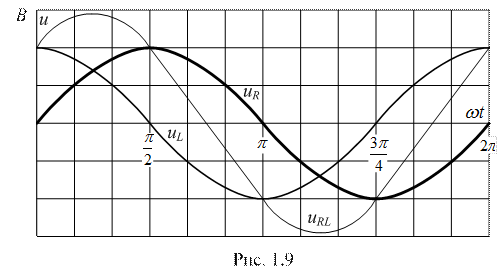
Рассчитать действующие значения напряжения uRL, составляющих uR и uL этого напряжения. Построить графики мгновенных значений напряжений uRL, составляющих uR и uL.
Решение. По осциллограмме рис. 1.7, б двойная амплитуда напряжения на шунте 2А = 10 дел. Находим амплитудное значение Im тока i:
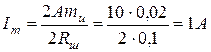
Реактивное сопротивление Х индуктивности L на частоте
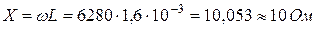
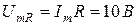
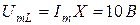
Мгновенные значения составляющих напряжения на сопротивление R катушки индуктивности и индуктивности L соответственно равны (ψi = 0):
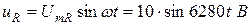
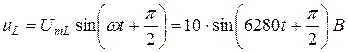
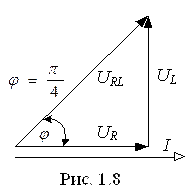
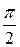
Действующие значения напряжений:
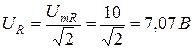
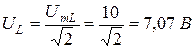
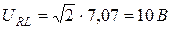
Векторные диаграммы напряжений и тока приведены на рис. 1.8.
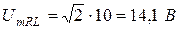
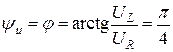
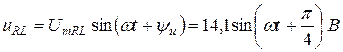
Задача 1.2. К цепи со схемой рис.1.10 приложено синусоидальное напряжение u = 141 sin 314t B.
Найти мгновенные и действующие значения тока и напряжения на всех участках цепи, если R = 30 Ом,
Решение. Назначаем положительные направления тока и напряжений как на рис. 1.10. Определяем реактивное сопротивление ХС емкости C на частоте ω = 314с -1 :
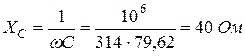
Полное сопротивление цепи:
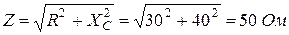
– тока i: 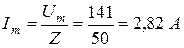
– напряжения на резисторе R: 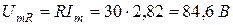
– напряжения на емкости С: 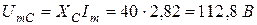
Угол сдвига фаз между напряжением u и током i:
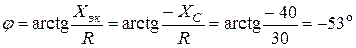
Начальная фаза тока i определяется из соотношения 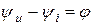
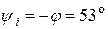
Мгновенные значения тока и напряжений на участках цепи:
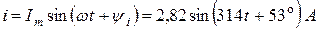
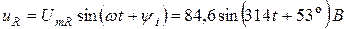
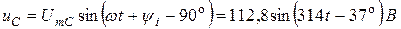
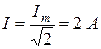
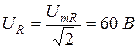
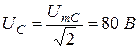
Задача 1.3. Для пассивного двухполюсника (рис. 1.5) экспериментально определены:
Найти полное и эквивалентные активное и реактивное сопротивления двухполюсника.
Решение. Имеем по определению:
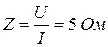
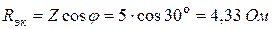
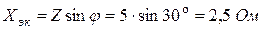
Задача 1.4 По цепи по схеме рис. 1.10 действующие значения тока i на частотах
Определить параметры цепи R и C, если на этих частотах напряжение на входе U = 100 В.
Решение. По определению на частотах f1 и f2 имеем:
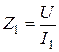
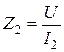
Непосредственно по схеме цепи рис. 1.10 находим:
Значения параметров R и С найдем из решения системы уравнений
Программа расчета в пакете MathCAD.
| U:=100 f1:=500 f2:=1000 I1:=1 I2:=1.8 | ←Присвоение переменным заданных условием задачи величин. |
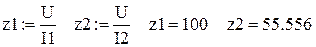 | ←Расчет полных сопротивлений на частотах f1 и f2. |
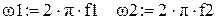 | ←Расчет угловой частоты. |
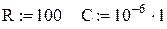 | ←Задание приближенных значений параметров R и C цепи. |
| Giver | |
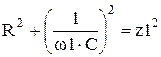 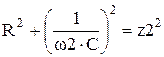 | ←Решение системы нелинейных уравнений. Для набора «=» нажмите [Ctrl]=. |
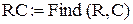 | ←Присвоение вектору RC найденных значений параметров R и C цепи. |
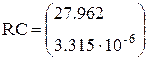 | ← 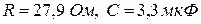 |
Значения параметров цепи: 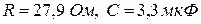
Задача 1.5. Вычислить действующее значение тока и активную мощность на входе пассивного двухполюсника с эквивалентными активной проводимостью
G = 0,011 Ом -1 и реактивной проводимостью B = 0,016 Ом -1 . Напряжение на входе двухполюсника U = 30 В.
Решение. Полная проводимость
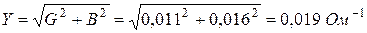
Действующее значение тока
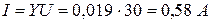
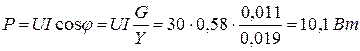
Задача 1.6. Действующее значение синусоидального тока ветви с резистором R равно 0, 1 А (рис. 1.11). Найти действующие значения напряжения u, и токов iL и i, если R = 430 Ом; XL = 600 Ом. Чему равна активная, реактивная и полная мощности этого двухполюсника?
Решение. Положительные направления напряжения и токов указаны на рис. 1.11.
Действующее значение тока IR = 0,1 А.
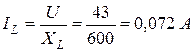
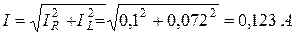
Действующее значение тока I можно вычислить, определив полную проводимость Y цепи. По виду схемы имеем
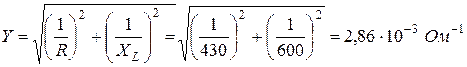
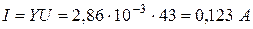
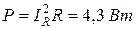
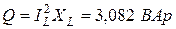
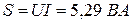
Выполняется соотношение 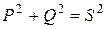
Задача 1.7. Действующее значение синусоидального напряжения на емкости С в цепи со схемой рис. 1.10 UС = 24 В. Найти действующее значение напряжения u и тока i, если XC = 12 Ом; R = 16 Ом.
Решение. Определяем действующее значение тока i
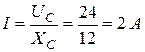
Полное сопротивление цепи
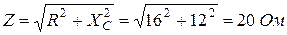
Определяем действующее значение напряжения u
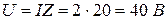
Задача 1.8. Для определения эквивалентных параметров пассивного двухполюсника в цепи синусоидального тока были сделаны измерения действующих значений напряжения, тока и активной мощности (рис. 1.12).
Для определения характера реактивного сопротивления (проводимости) параллельно двухполюснику была включена емкость С (ВС ? Вэк). При этом показания амперметра уменьшились. Рассчитать эквивалентные сопротивления и проводимости двухполюсника.
Решение.
Действующее значение: I = 0,5 A, U = 100 B. Активная мощность, потребляемая двухполюсником, P = 30 Вт. Полное сопротивление двухполюсника
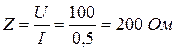
Эквивалентное активное сопротивление
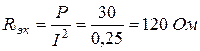
Эквивалентное реактивное сопротивление
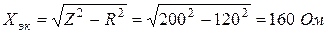
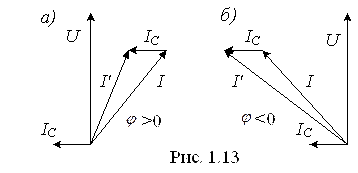
Полная проводимость двухполюсника
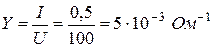
Эквивалентная активная проводимость
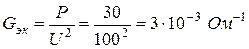
Эквивалентная реактивная проводимость
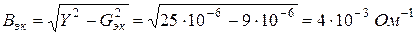
Следует обратить внимание, что треугольники сопротивлений и проводимостей для одного и того же двухполюсника подобны (рис. 1.4). Поэтому,
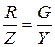
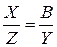
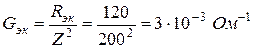
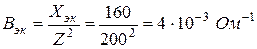
1.3. Задачи и вопросы для самоконтроля
1. Какими параметрами описываются синусоидальные токи в электрических цепях?
2. Как связаны между собой круговая частота ω и период Т синусоидального тока?
3. Что такое действующее значение переменного тока?
4. Запишите формулы для вычисления индуктивного и емкостного сопротивлений.
5. Объясните, как определить напряжение на участке цепи, если заданы 
6. Нарисуйте треугольник сопротивлений и треугольник проводимостей с необходимыми обозначениями.
7. Запишите формулы для вычисления активной и реактивной мощностей.
8. Напряжение на индуктивности L = 0,1 Гн в цепи синусоидального тока изменяется по закону 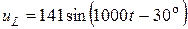
9. Ток в емкости С = 0,1 мкФ равен 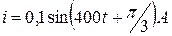
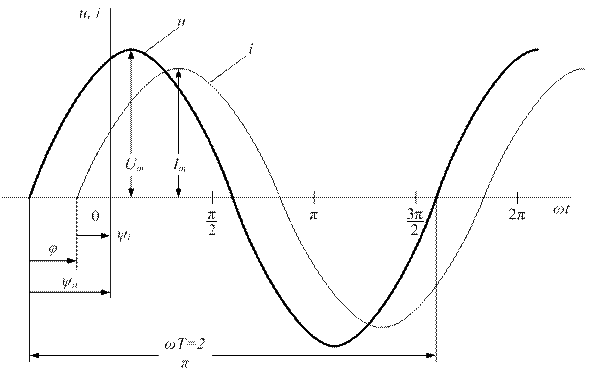
10. На участке цепи с последовательно включенными активным сопротивлением R = 160 Ом и емкостью С = 26,54 мкФ мгновенное значение синусоидального тока 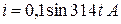
Дата добавления: 2016-01-29 ; просмотров: 105779 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Раздел 4. Однофазные электрические цепи синусоидального тока
Раздел 4. ОДНОФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Определить угловую частоту вращения ΩР, ротора генератора переменного тока при частоте питающего напряжения f = 50 Гц и угловую частоту ω ЭДС, если ротор вращается с частотой n1 = 1000 об/мин.
1. Число пар полюсов генератора: 
2. Угловая частота вращения ротора:
3. Угловая частота переменного тока:
или
Ответ: ΩР= 104,5 с-1; ω=314 с-1
Определить среднее значение синусоидального тока Iср по мгновенному его значению i=31,4sin(ωt+π/2)
Среднее значение синусоидального тока:
Для синусоидального напряжения и тока (рис. 4.4) записать выражения для мгновенных их значений. Определить период Т и время t0, соответствующее начальной фазе тока Yi, а также мгновенные значения напряжений u1 и u2 для моментов времени t1 = 0,00167 с и t2 = 0,005 с, если частота тока f = 50 Гц.
Решение
1. Мгновенные значения напряжения и тока имеют вид:
где Um, lm — амплитудные значения напряжения и тока.
2. Начальная фаза тока (в радианах):
3. Период переменного напряжения и тока:
4. Время начала отсчета, т. е. время, соответствующее начальной фазе тока:
5. Мгновенное значение напряжения в момент времени t1:
α1 = ωt1= 2πft1 = 2π×50×0,00167= π×0,167= π× 
6. Мгновенное значение напряжения в момент времени t2:
α1 = ωt1= 2πft1 = 2π×50×0,005= 0,5π = π× 
Ответ: T = 0,02 с; 

Определить максимальное Ет и действующее Е значения ЭДС, наводимой в прямоугольной катушке с числом витков w = 200, вращающейся в однородном магнитном поле с постоянной частотой вращения п = 1500 об/мин. Размеры витка катушки 3×3 (площадь витка SB = 3×3 = 9 см2). Индукция магнитного поля В= 0,8 Тл.
Построить кривые изменения магнитного потока и ЭДС во времени е, Ф(t), а также векторную диаграмму цепи.
1. Частота индуцированной в катушке ЭДС:
2. Максимальное значение магнитного потока:
3. Амплитудное значение ЭДС, наводимой в катушке, находят исходя из мгновенного ее значения:
4. Действующее значение ЭДС катушки :
Е = Ет/

 |

Переменный электрический ток задан уравнением
Определить период, частоту этого тока и мгновенные значения его при t0 = 0; t1=0,152 с. Построить график тока.
1. Уравнение синусоидального тока в общем случае имеет вид:
Сопоставляя это уравнение с заданным частным уравнением тока, устанавливаем, что амплитуда Im = 100 А, угловая частота w = 628 рад/с, начальная фаза
2. Период
3. Частота f =
4. Мгновенные значения тока найдем, подставив в уравнение тока заданные значения времени:
при t0 = 0: i0 = 100sin(wt0 — 60°)= 100sin(628×0 — 60°)= 100sin(-60°)= -86,5 А;
при t1 = 0,152 с: (значение ωt преобразуем в градусы, умножив на
i1 = 100 sin(628×0,152 
Значения синусоидальной величины через 360° повторяются, поэтому мгновенное значение тока при угле ωt1= 15,2×360° будет таким же, как и при угле 0,2×360° = 72°;
5. Для построения графика i(ωt) нужно определить ряд значений тока, соответствующих различным моментам времени (табл. 4.1 и рис. 4.8).











Определить коэффициенты амплитуды Kа и формы Кф
периодического напряжения u(t), линейная диаграмма изменения
мгновенного значения во времени которого приведена на
1. Для синусоиды Ка:
В сеть переменного тока при напряжении U = 120 В и частоте f = 50 Гц включена катушка с индуктивностью L = 0,009 Г (RK = 0). Определить реактивную мощность Q катушки и энергию WLm, запасаемую в магнитном поле катушки, записать выражения для мгновенных значений напряжения и, тока i, ЭДС самоиндукции eL за период, если начальная фаза напряжения Yu= π/2. Построить векторную и временную диаграммы.

1. Индуктивное сопротивление катушки:
2. Действующее значение тока:
3.Реактивная мощность цепи:
Q= UI = 120-40 = 4800 ВАр = 4,8 кВАр
4. Максимальная энергия, запасаемая в магнитном поле катушки:

Im = I
WLm = 0,009×56,42 = 14 Дж
5. Амплитудное значение напряжения и тока:
Um =U
6. Амплитудные значения:
ЭДС самоиндукции катушки:

7. Построим векторную диаграмму для действующих значений:
— по оси абсцисс отложим вектор тока;
— вектор напряжения опережает ток на π/2;
— вектор ЭДС самоиндукции находится в противофазе напряжению и отстает от тока на π/2.
К сети переменного тока при напряжении U = 220 В и частоте f = 50 Гц подключен конденсатор с емкостью С = 20 мкФ.
Определить его реактивное сопротивление Хс, ток I, реактивную мощность Qc, максимальную энергию WCm, запасаемую в электрическом поле конденсатора.
Построить векторную диаграмму для данной цепи.
1. Реактивное сопротивление конденсатора:
2. Ток в цепи конденсатора:
3. Реактивная мощность цепи:
Qc= UI= 220×1,37 = 302 ВАр.
4. Максимальная энергия, запасаемая в электрическом поле конденсатора:

7. Построим векторную диаграмму для действующих значений:
— по оси абсцисс отложим вектор тока;
— вектор напряжения отстает от вектора тока на π/2;
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Часть 1. 1. Мгновенные значения токов и напряжений в нагрузке заданы выражениями: i = 2 sin (376,8t+30°) А,
Читайте также:
|
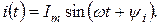
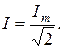
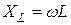
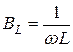
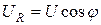
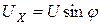
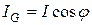
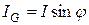
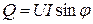

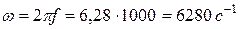

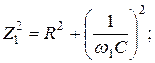
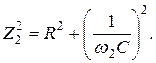
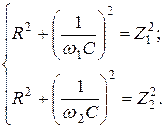
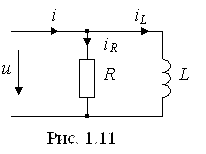



















 ; f =
; f =  ; i0 = -86,5 А; i1= 20,8 A.
; i0 = -86,5 А; i1= 20,8 A.

 ; i1= 5 A; i2 = 8,65 A ; i3= 10 A
; i1= 5 A; i2 = 8,65 A ; i3= 10 A На рис. 4.7 изображены графики двух э. д.с. Написать уравнения кривых и определить угол сдвига фаз между ними. Определить из графиков мгновенные значения э. д.с. для момента времени t1 = 0,007 с и сравнить с результатами, полученными из уравнений.
На рис. 4.7 изображены графики двух э. д.с. Написать уравнения кривых и определить угол сдвига фаз между ними. Определить из графиков мгновенные значения э. д.с. для момента времени t1 = 0,007 с и сравнить с результатами, полученными из уравнений. =314 рад/c
=314 рад/c ;
; 



 = 50 Гц
= 50 Гц
 60°
60°




 Задача 4.12.
Задача 4.12.