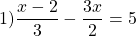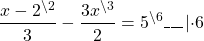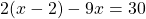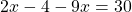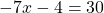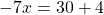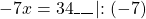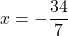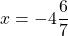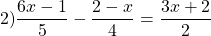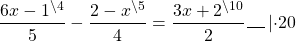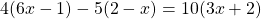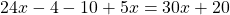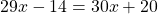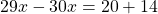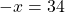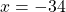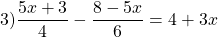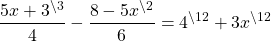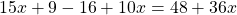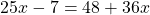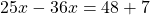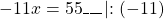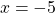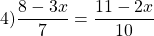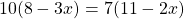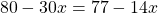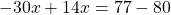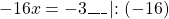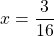Линейные уравнения с дробями не содержат переменной в знаменателе. Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число.
Наименьший общий знаменатель данных дробей равен 6. Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
В результате наименьший общий знаменатель и знаменатель каждой дроби сокращаются, и получаем линейное уравнение, не содержащее дробей.
Раскроем скобки и приведём подобные слагаемые:
Обе части уравнения делим на число, стоящее перед иксом:
Из полученной неправильной дроби выделяем целую часть
Наименьший общий знаменатель данных дробей равен 20. Найдем дополнительный множитель к каждой дроби и умножим обе части уравнения на 20:
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби. Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге. Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:
Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».
После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую (не забыв при переносе изменить их знаки), а можно сначала упростить каждую часть, приведя подобные слагаемые, а потом уже переносить.
Здесь наименьший общий знаменатель дробей равен 12. Находим дополнительный множитель к каждой дроби и умножаем обе части уравнения на 12:
Раскрываем скобки и упрощаем
Обе части уравнения делим на число, стоящее перед иксом:
Уравнения такого вида можно решить, использовать основное свойство пропорции (в верной пропорции произведение крайних членов равно произведению средних членов):
при делении двух отрицательных чисел получается положительное число, поэтому минусы можно сразу же не писать.
Если это возможно, лучше ответ записать в виде десятичной дроби:
- Тренажер по математике на тему «Решение уравнений, сводящихся к линейным» (7 класс)
- Практические аспекты применения современных технологий при обучении школьников математике в рамках ФГОС ООО
- Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС
- Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения
- «Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Решение уравнений с дробями
- Понятие дроби
- Основные свойства дробей
- Понятие уравнения
- Понятие дробного уравнения
- Как решать уравнения с дробями
- 1. Метод пропорции
- 2. Метод избавления от дробей
- Что еще важно учитывать при решении
- Универсальный алгоритм решения
- Примеры решения дробных уравнений
- Тренажер по решению линейных уравнений. тест по алгебре (7 класс) по теме
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 📽️ Видео
Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Тренажер по математике на тему «Решение уравнений, сводящихся к линейным» (7 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Видеолекции для
профессионалов
- Свидетельства для портфолио
- Вечный доступ за 120 рублей
- 311 видеолекции для каждого
Государственное бюджетное общеобразовательное учреждение школа №60
Выборгского района Санкт-Петербурга
Учитель: Воронова Лариса Валентиновна
Методическая разработка тренажера по математике
для 6 — 7 класса по теме:
«Решение уравнений, сводящихся к линейным»
Тренажер предназначен для учащихся 6–7 классов с целью отработки и совершенствования навыков решения уравнений первой степени, содержащих дробную часть.
— пошаговую инструкцию преобразования заданного уравнения к более простому виду, что в итоге приводит к линейному уравнению вида ax = b ;
— задания в двух уровнях: уровень А (базовый) и уровень В (повышенный).
— ответы к заданиям;
— примеры решения уравнений.
Тренажер может быть использован для самостоятельной работы учащихся в классе и дома, на дополнительных индивидуальных занятиях, а также при подготовке к итоговой аттестации.
Материал тренажера можно использовать для составления раздаточного материала.
Тренажер по теме:
«Решение уравнений, сводящихся к линейным»
Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
Сократить получившиеся дроби.
Упростить левую и правую части уравнения (раскрыть скобки).
Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
Привести подобные слагаемые в левой части и найти значение правой части.
Найти значение x , разделив обе части уравнения на коэффициент при неизвестном a .
У р о в е н ь А
Тренажер по теме:
Решение уравнений, сводящихся к линейным
1. Найти общий знаменатель всех дробей, входящих в уравнение (наименьшее общее кратное всех знаменателей).
2. Умножить каждый член в левой и правой частях уравнения на общий знаменатель.
3. Сократить получившиеся дроби.
4. Упростить левую и правую части уравнения (раскрыть скобки).
5. Перенести неизвестные члены уравнения в левую часть, а известные – в правую, изменив при этом их знак на противоположный.
6. Привести подобные слагаемые в левой части и найти значение правой части.
7. Найти значение x , разделив обе части уравнения на коэффициент при неизвестном a .
У р о в е н ь В
9 —
2 x —
6 —
Ответы к тренажеру
« Решение уравнений, сводящихся к линейным»
—
12
2
49
Примеры решения уравнений
I способ II способ
1 ) 


Основное свойство пропорции: произведение крайних членов пропорции
равно произведению ее средних членов.
2)
3) 

8(5 y + 8) – 7(3 y — 1) = 56·5
40 y + 64 – 21 y +7 = 280
19 y = 280 – 64 – 7


3х – 15 = 10х +5 – 105
х = 
4)
5)
– 

–3(1 – 5 m ) + 2(1 +3 m ) = 0
–3 + 15 m + 2 + 6 m = 0
m =
2 x — 

6 · 2 x – 2(16 – x ) = 3( x +3) +6 · 6
Ответ : 1) —5 ; 2) 11 ; 3) 12 

«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Практические аспекты применения современных технологий при обучении школьников математике в рамках ФГОС ООО
- Сейчас обучается 30 человек из 19 регионов
Курс повышения квалификации
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС
Курс повышения квалификации
Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения
- Сейчас обучается 79 человек из 33 регионов
«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Видео:Уравнения с дробями. Алгебра 7 класс.Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 858 069 материалов в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 15.11.2015
- 598
- 1
- 15.11.2015
- 565
- 1
- 15.11.2015
- 11019
- 196
- 15.11.2015
- 648
- 1
- 15.11.2015
- 511
- 2
- 15.11.2015
- 2314
- 1
- 15.11.2015
- 1295
- 8
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.11.2015 24639
- DOCX 221 кбайт
- 675 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Воронова Лариса Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 10 месяцев
- Подписчики: 0
- Всего просмотров: 139886
- Всего материалов: 15
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
«Развитие эмоционального интеллекта»
«Активные методы обучения как способ повышения эффективности образовательного процесса»
«Роль социального педагога в инклюзивном образовании»
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Тысячи учителей в Австралии вышли на забастовку
Время чтения: 2 минуты
Онлайн-тренинг «Как закрыть гештальт: практики и упражнения»
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:КАК РЕШИТЬ УРАВНЕНИЕ С ДРОБЯМИ, СВОДЯЩЕЕСЯ К ЛИНЕЙНОМУ? Примеры | АЛГЕБРА 7 классСкачать

Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Видео:Сложное уравнение с дробями. Алгебра 7 класс.Скачать

Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Видео:Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Видео:№7 Линейное уравнение (5х+4)/2+3=9x/5 Простое уравнение с дробями Решите уравнение с дробью ОГЭ ЕГЭСкачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Видео:Алгебра 7 класс. 11 сентября. Решение линейных уравнений #1Скачать

Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Тренажер по решению линейных уравнений.
тест по алгебре (7 класс) по теме
Тренажер «Решение линейных уравнений»
Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Скачать:
| Вложение | Размер |
|---|---|
| trenazher_po_resheniyu_liineynyh_uravneniy.docx | 20.22 КБ |
| trenazher_po_resheniyu_liineynyh_uravneniy.docx | 20.22 КБ |
Видео:Как решать линейные уравнения. План решения любого линейного уравнения. Алгебра 7 класс.Скачать

Предварительный просмотр:
Тренажер по теме «Решение линейных уравнений»
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель
Решите уравнение по образцу:
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.
2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5.
Видео:Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

Предварительный просмотр:
Тренажер по теме «Решение линейных уравнений»
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель
Решите уравнение по образцу:
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.
2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5.
Видео:Как решать линейные уравнения #математика #математика7классСкачать

По теме: методические разработки, презентации и конспекты
Открытый урок по математике в 6 классе «Решение линейных уравнений»
здесь представлен план — конспект урока по математике в 6 классе «Решение линейных уравнений» с применением ЭОР.
Проект по теме «Решение линейных уравнений с параметрами»
Проект по теме «Решение линейных уравнений с параметрами».
Разработка методических рекомендаций решения линейных уравнений с параметрами.
Разработка методических рекомендаций решения линейных уравнений с параметрами.
Функционально-графический подход к решению линейных уравнений с параметром и модулем
План-конспект урока с использованием ЦОР для обобщающих уроков по теме «Линейные уравнения с параметром и модулем» для учащихся 7-9 классов и для подготовки к ГИА (презентация к уроку).
Презентация:»Решение линейных уравнений»
Презентация по алгебре «Решение линейных уравнений».Данная презентация может быть использована на уроке алгебры в 7 классе при изучении темы: «Линейное уравнение с одной переменной». Данная тема изуча.
Задание по теме «Решение линейных уравнений», составление фигуры «Танграм»
Задания по теме решение линейных уравнений для 6, 7 классов. Задания комбинированные. Вначале решить все уравнения, а затем составить фигуру танграм.
Тематический тренажер для подготовки к ГИА в 2014 г. по математике 9 класс. Тематические тренировочные задания. Отработка заданий: модуль «Алгебра» Тема№2 «Решение линейных уравнений»
Представляю вашему вниманию очередной тематический тренажер для подготовки к ГИА в 2014г по алгебре по теме «Решение линейных уравнений». Подобраны упражнения, которые соответствуют типовым заданиям К.
📽️ Видео
Сложные уравнения. Как решить сложное уравнение?Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Переставь одну цифру! Задача на логикуСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать