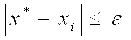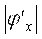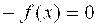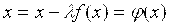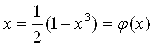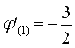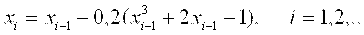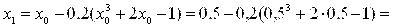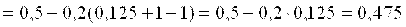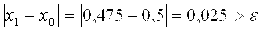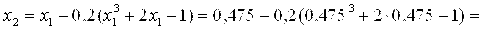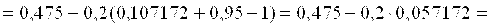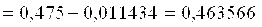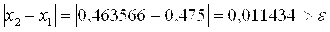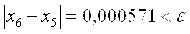Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1=
X2=
Так как f / (









Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при 
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 
Видео:Вычислительная математика 4 Решение систем нелинейных уравненийСкачать

Сходимость методов решения нелинейных уравнений
Если метод сходится, то есть
где — точное решение,
— k-е приближение к точному решению, то итерационный процесс следовало бы закончить по достижении заданной погрешности
где — заданная точность (погрешность).
Однако практически это условие выполнить нельзя, так как неизвестно, тогда для окончания итерационного процесса можно воспользоваться неравенствами
где и — заданные величины.
При таком окончании итераций погрешность может возрасти по сравнению с и, поэтому, чтобы она не увеличивалась, величины и соответственно уменьшают или увеличивают число итераций.
Методы простой итерации, Зейделя, модифицированный метод Ньютона, метод наискорейшего спуска являются методами первого порядка — это значит, что имеет место неравенство
где — константа, своя у каждого метода, зависящая от выбора начального приближения , функции fi , i = 1, 2, . . . , n, и их частных производных первого и второго порядков — точнее, их оценок в некоторой окрестности искомого решения, которой принадлежит начальное приближение.
Метод Ньютона является методом второго порядка, то есть для него имеет место неравенство
где — константа, зависящая от тех же величин, что и константа .
А теперь рассмотрим достаточные условия сходимости метода простой итерации и метода Ньютона.
Сходимость процесса простой итерации зависит от двух условий. Первое условие состоит в том, что какая-нибудь точка должна оказаться близкой к исходному решению . Степень необходимой близости зависит от функций 1, 2, . . . , n . Это требование не относится к системам линейных уравнений, для которых сходимость процесса простой итерации зависит только от второго условия.
Второе условие связано с матрицей, составленной из частных производных первого порядка функций 1, 2, . . . , n — матрицей Якоби
вычисленной в точке .
В случае, когда рассматривается система линейных алгебраических уравнений, матрица M состоит из постоянных чисел — коэффициентов, стоящих при неизвестных в правой части уравнения (5.3). В случае нелинейных уравнений элементы матрицы M зависят, вообще говоря, от .
Для сходимости процесса простой итерации достаточно, чтобы выполнялось неравенство: для из некоторой окрестности точного решения , которой должно принадлежать начальное приближение .
Приведем также достаточные условия сходимости метода Ньютона для системы уравнений вида (5.1) по норме .
Понятие о нелинейных системах уравнений в Rn.
- 1. Понятие приближенного и точного решений нелинейной системы уравнений.
- 2. Сущность графического метода отделения решения для системы двух нелинейных уравнений. Каковы его преимущества и недостатки?
- 3. Сущность метода простой итерации и метода Зейделя. Каковы условия применимости метода простой итерации?
- 4. Сущность метода Ньютона и его модификации. Какова скорость сходимости метода Ньютона?
- 5. Сущность метода наискорейшего спуска. Как выбирается параметр спуска?
Видео:10 Численные методы решения нелинейных уравненийСкачать

3.2.1. Метод простых итераций (метод последовательных приближений)
Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
Что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
Xi=φ(xi-1) , i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула — формулой итерационного процесса метода.
Если 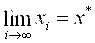
Условие сходимости 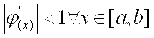
Точное решение x* получить невозможно, так как требуется Бесконечный Итерационный процесс.
Можно получить Приближенное Решение, прервав итерационный (3.8) при достижении условия
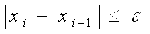
Где ε — заданная точность; i — номер последней итерации.
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
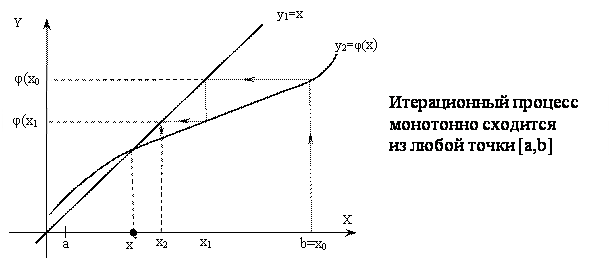
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Рис. 3.7 Итерационный процесс для случая 0 1 
 |
Рис. 3.10 Итерационный процесс для случая 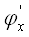
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
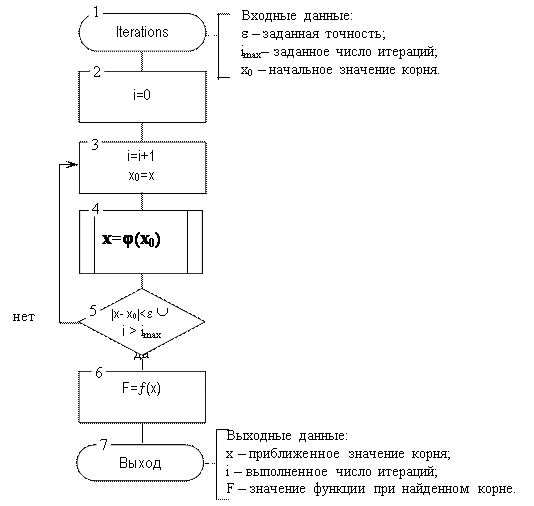 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .
Простейшие эквивалентные преобразования, например:
F(x) = 0 => x+f(x) = x, т. е. φ(x) = x + f(x)
Или выразить явно x из (3.1)
F(x) = 0 => x — φ(x) = 0 => x = φ(x)
Не гарантируют сходимость.
Рекомендуется следующий способ получения формулы Сходящегося итерационного процесса.
Пусть 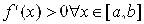
Если это не так, переписать уравнение (3.1) в виде
Умножить обе части уравнения на 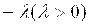
Константу l вычислить по формуле:
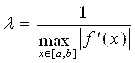
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
Xi = xi+1− λ f(x) (3.12)
Где i=1,2,… — номер итерации, x0Î[a, b] – начальное приближение.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
Проверим условия сходимости для полученной формулы:
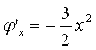
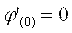
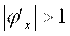
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
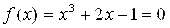
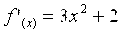
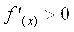
Наибольшее значение 
Следовательно 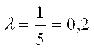
Формула Сходящегося итерационного процесса
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение
Проверим условие завершения итерационного процесса
Расчет следует продолжить.
X6 = 0,453917 − ответ, т. к.
Проверим полученное значение, подставив в исходное уравнение:
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
📸 Видео
Решение нелинейного уравнения методом простых итераций (программа)Скачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Лукьяненко Д. В. - Численные методы - Лекция 1Скачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Численные методы. Лекция 2. Матричные задачи. Решение нелинейных уравненийСкачать

Метод итераций (последовательных приближений)Скачать

Вычислительная математика, 5 семестр. Лекция 4Скачать

Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Нелинейные уравненияСкачать

10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать

Кобельков Г. М. - Численные методы. Часть 1. Лекции - Итерационные методы решения линейных уравненийСкачать

Метод простой итерации Пример РешенияСкачать

Численные методы. Часть 1Скачать

Численные методы. Лекция 7Скачать

1 Введение в численные методы ЧМ: что такое ЧМ, виды ЧМ, условие на сходимость, условие на точностьСкачать