Домножим первое уравнение на чтобы

40. Алгебра Читать 0 мин.

Видео:7 класс, 39 урок, Метод алгебраического сложенияСкачать

40.701. Системы уравнений

Ключевым моментом в решении систем уравнений является понимание самой сути системы. Система означает, что необходимо учитывать решения нескольких уравнений или нескольких неравенств при записи решения. То есть нужно решить. И первое, И второе уравнение/неравенство, ответом самой системы будет пересечение этих ответов.

Рассмотрим несколько простейших систем.

$ beginx = 2\x = 5endleftrightarrow emptyset $

Решением системы являются все значения переменной, при которых выполняются все перечисленные условия. Может ли x одновременно равняться и 2, и 5? Нет, поэтому у этой системы решений нет.

Часто системы усложняются неравенствами.

В этой системе требуется, чтобы x был одновременно и равен 5, и был больше 2. При каких значениях это возможно? Только при x =5.

Рассмотрим ещё одну систему:

$ beginx > 2\x 2\x = 5endleftrightarrow x in ( 2;=+infty)$

Там подходят или 5, или те x, которые больше 2. Но 5 больше 2, значит, нам просто подходит промежуток от 2 до бесконечности.

$beginx 5endleftrightarrow x in ( -infty;=2 )cup (5;+infty) $

Здесь мы будем рассматривать объединение: если x является корнем хотя бы одного уравнения, неравенства из совокупности, значит, он уже является решением.

Но и это ещё не всё. Иногда совокупность включает в себя систему или система включает себя совокупность. Давайте посмотрим.

$left[beginbeginx = 5\x >2end \ beginx = 2\x > 5end endleftrightarrow left[ beginx=5\emptyset endleftrightarrow x=5 right.right. $

Такая ситуация называется «совокупность двух систем». То есть в ответ пойдут все x, которые удовлетворяют первой системе, и все x, которые удовлетворяют второй системе. Поэтому для того чтобы её решить, нужно сначала решить внутренние системы, а затем в ответ написать все полученные в них корни.

Следующий пример немного другой:

$ beginx > 2\ left[ begin x =1\x = 5 endright.endleftrightarrow x = 5leftrightarrow left[ begin beginx = 1\x >2end \ beginx = 5\x > 2end endleftrightarrow left[ begin emptyset\ x=5 endleftrightarrow x=5 right.right. $

Итак, у нас есть система. Это означает, что должно выполняться 2 условия:

1. x должен быть больше 2.

2. x должен быть равен либо 1, либо 5.

В таких случаях необходимо рассмотреть каждый корень из второго условия на соответствие первому, то есть перейти к совокупности двух систем.

Методы решения систем

Существует несколько основных методов решения систем:

1. Метод подстановки

2. Метод алгебраического сложения

3. Графический метод решения

4. Метод замены переменной

Рассмотрим их на примере следующей системы:

Метод подстановки

1. Выразим y через x из первого уравнения.

$begin5x-2y=8\3x+ 5y=11endleftrightarrow begin-2y=8-5x\3x+ 5y=11endleftrightarrow beginy=-4+2, 5x\3x+ 5y=11end $

2. Подставим данное выражение вместо y во второе уравнение и решим данное уравнение.

$ beginy=-4+2,5x\3x+ 5cdot (-4+2,5x)end leftrightarrow beginy=-4+2,5x\3x-20+12,5x=11endleftrightarrow beginy=-4+2,5x\15,5x=31end leftrightarrow beginy=-4+2,5x\x=2end $

3. Подставим найденное значение x в первое уравнение и найдём y.

$beginy=-4+2,5x\x=2endleftrightarrow beginy=-4+2,5cdot 2\x=2end leftrightarrow beginy=1\x=2end$

4. Ответ запишем парно.

Метод алгебраического сложения

1. Приведём к такому виду, когда перед одной из переменных в уравнениях стоят равные по модулю коэффициенты, но с противоположными знаками. Например, домножим первое уравнение на 5, а второе – на 2.

$begin5x-2y=8\3x+ 5y=11endleftrightarrow begin25x-10y=40\6x+ 10y=22end$

2. Сложим первое уравнение и второе и запишем эту сумму на месте первого уравнения. Второе уравнение оставим неизменным.

$ begin25x-10y=40\6x+ 10y=22endleftrightarrow begin25x-10y+6x+10y=40+22\6x+ 10y=22 endleftrightarrowbegin31x=62\6x+ 10y=22end leftrightarrowbeginx=2\6x+ 10y=22end$

3. Подставим найденное значение x во второе уравнение и найдём y.

$beginx=2\6x+ 10y=22endleftrightarrow beginx=2\6 cdot 2+ 10y=22endleftrightarrowbeginx=2\y=2end$

4. Ответ запишем парно.

Графический метод решения

1. Выразим y через x, чтобы к виду уже известных нам функций.

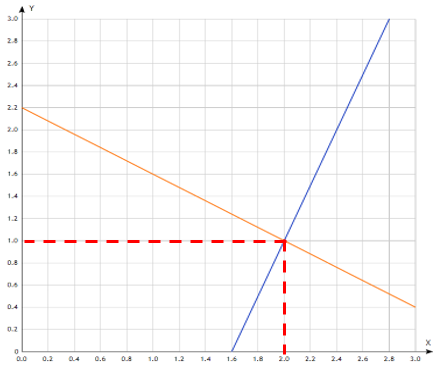
$ begin5x-2y=8\3x+ 5y=11endleftrightarrow begin-2y=8-5x\5y=-3+11endleftrightarrow beginy=2,5x-4\y=-0,6x+2,2end$

2. Рассмотрим две функции и построим их графики:

3. Найдём точку пересечения графиков. Видим, что это точка с координатами (2;1).

4. Подставим координаты точки в уравнение и проверим, что равенство выполняется.

$begin5 cdot 2-2cdot1=8\3cdot2+5cdot1=11end leftrightarrowbegin8=8\11=11end$

5. Проанализируем монотонность и докажем, что других решений нет.

Функция $y_1(x)=2,5x-4$ монотонно возрастающая.

Функция $y_2(x)=-0,6x+2,2$ монотонно убывающая.

Значит, они имеют только одну точку пересечения. Тогда найденная точка является единственным решением.

6. Ответ запишем парно.

Метод замены переменной

Представим, что вместо изначальной системы мы решаем систему вида:

1. Сделаем замену переменных.

2. Перепишем систему с новыми переменными.

3. Решим систему любым удобным способом.

Получаем ответ (2;1).

4. Вернёмся к исходным переменным.

5. Ответ запишем парно.

Таким образом можно решить любое сложное уравнение, если увидеть повторяющиеся элементы и правильно их заменить.

При решении сложных систем уравнений важно мысленно попробовать все способы, чтобы сразу определить наиболее быстрый и правильный путь решения.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Решение систем уравнений методом сложенияСкачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Немного теории.

Видео:Решение систем уравнений методом сложенияСкачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:Решение систем уравнений методом сложенияСкачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Видео:Решение систем уравнений методом подстановкиСкачать

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Системы уравнений. Метод алгебраического сложения.Скачать

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Видео:МЕТОД ПОДСТАНОВКИ 7 класс СИСТЕМА УРАВНЕНИЙСкачать

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Решение задач с помощью систем линейных уравнений.Скачать

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Видео:Системы линейных уравнений с двумя неизвестными. Способ сложения, 7 классСкачать

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Видео:Как решать системы уравнений методом математического сложенияСкачать

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Видео:Система линейных уравнений методом алгебраического сложенияСкачать

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

🔍 Видео

Как решить уравнение #россия #сша #америка #уравненияСкачать

Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

7 класс. Решение систем уравнений способом сложенияСкачать

Способ сложения. Система линейных уравнений с двумя переменными.Скачать

7 класс. Решение систем линейных уравнений способом сложенияСкачать

Рациональное уравнение №1Скачать