Из предложенных тем я выбрала: «Методы решения показательных уравнений и неравенств», так как она наиболее актуальна не только для меня, но и для детей моего возраста. В связи с приближающимися экзаменами, данный проект так же поможет мне при решении заданий из ЕГЭ.
В данной работе исследуются разные способы решений показательных уравнений и неравенств.
В процессе выполнения проекта я приобрела навыки проектной деятельности, развила коммуникативные и аналитические способности, а также навыки самостоятельного поиска необходимого материала с помощью учебной и художественной литературы и интернет-источников, более того получила знания как по математики, так и по истории.
Для достижения цели исследовательской работы необходимо было решить следующие задачи:
— осваивание математических знаний и умений, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне.
-изучить различные методы решения показательных уравнений и неравенств.
— развитие логического мышления и алгоритмической культуры;
Обычно математику считают прямой противоположностью поэзии. Однако математика и поэзия — ближайшие родственники, ведь и то и другое — работа воображения.
Томас Хилл
Определенно, чтобы понять и научиться решать любые математические задания, мало просто знать все многочисленные формулы и свойства, которыми богата данная наука. Если не подходить к заданию творчески, широко и открыто мыслить, то легко попадешь «в тупик», что может привести не только к разочарованию в науке, но и в самом себе. Математика как игра привлекательна свое содержательностью, сложностью и неожиданностью результатов. Так же для овладения почти любой современной профессии требуются математические познания. Строгое и абстрактное мышление, необходимое в реальной действительности, легче развить, занимаясь математикой, поскольку эта наука строга и абстрактна. Именно поэтому, на примере решения показательных уравнений и неравенств, я хочу показать, что данный процесс может не только увлечь вас, но и так же заставить ваш мозг работать куда продуктивнее.
История Показательных уравнений
Термин «показатель» для степени ввел в 1553 г. немецкий математик (сначала монах, а затем − профессор) Михаэль Штифель (1487-1567). По-немецки показатель − Exponent: «выставлять напоказ». Штифель же ввел дробные и нулевой показатели степени. Само обозначение ax для натуральных показателей степени ввел Рене Декарт (1637 г.), а свободно обращаться с такими же дробными и отрицательными показателями стал с 1676 г. сэр Исаак Ньютон.
Степени с произвольными действительными показателями, без всякого общего определения, рассматривали и Готфрид Вильгельм Лейбниц, и Иоганн Бернулли; в 1679 г. Лейбниц ввел понятия экспоненциальной (т.е., по-русски, показательной) функции для зависимости y=ax и экспоненциальной кривой для графика этой функции.
Уравнение, которое содержит неизвестное в показателе степени, называется показательным уравнением.
Самое простое показательное уравнение имеет вид:
Показательные уравнения путём алгебраических преобразований приводят к стандартным уравнениям, которые решаются, используя следующие методы:
- метод приведения к одному основанию;
- метод введения новых переменных;
- метод вынесения общего множителя за скобки;
- метод почленного деления;
- метод группировки;
- метод оценки.
Метод приведения к одному основанию
Способ основан на следующем свойстве степеней: если равны две степени и равны их основания, то равны и их показатели, т. е. уравнение надо попытаться свести к виду:
Представим правую часть в виде 3 log 3 7 x+1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
И запишем уравнение равносильное исходному
3 2x-1 = 3 log 3 7 x+1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Перейдем к уравнению для показательных степеней
2x-1= log 3 7 x+1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2x-1=x log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image005.png» /> + log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x(2- log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image005.png» /> )= log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x= 1+ log 3 7 2- log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x= log 3 3+ log 3 7 log 3 3 2 — log 3 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x= log 3 21 log 3 9 7 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x= log 9 7 21 ≈12.1144 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Ответ: 12.1144 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Метод введения новых переменных
Введение новой переменной обычно производится после преобразований членов уравнения.
4 x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image012.png» /> — 2 x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Обозначим t= 2 x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image013.png» /> ,где t>0, тогда
t 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
t 1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
t 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Так как -1 2 x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image013.png» /> =2 , откуда
x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Метод вынесения общего множителя за скобки
Тождественное преобразование, в результате которого многочлен
приводится к произведению нескольких множителей, называют
разложением многочлена на множители.
x2·2x+1 + 2|x-3|+2 = x2·2|x-3|+4 + 2x-1
То, что находится в правой части, мы перенесем в левую часть и сгруппируем многочлены с одинаковыми показателями
(x2·2x+1 -2x-1)+(2|x-3|+2- x2·2|x-3|+4) = 0
Вынесем общие множители за скобки
2x-1(4×2-1) +2|x-3|+2(1-4×2) = 0,
Последнее уравнение равносильно совокупности
Из первого уравнения совокупности находим x1 = — 1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image019.png» /> ,x2= 1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Из второго уравнения получаем:
x — 1= x — 3 +2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x — 3= x — 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x — 3= x — 3, если x ≥3 x — 3=- x +3, если x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
0∙ x =0, если x ≥3 2 x =6, x =3, если x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Ответ: — 1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image025.png» /> ∪ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image026.png» /> 1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image027.png» /> ∪ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image026.png» /> 3; +∞ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Метод почленного деления
Данный метод заключается в том, чтобы разделить каждый член уравнения, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Этот метод применяется для решения однородных показательных уравнений.
22х·2– 7·2х·5х+52х·5=0 /52х≠ 0
2· 2 5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image029.png» /> 2х– 7· 2 5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image029.png» /> х +5=0
Пусть 2 5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image029.png» /> х =t, t>0
2t2-7t+5=0
D=b2-4ac=49-4·2·5=9
t1=1, t2= 5 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image030.png» />
2 5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image029.png» /> х=1, 2 5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image029.png» /> х = 5 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image030.png» />
х=0, х=-1
3·22х+ 1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image020.png» /> ·9х+1– 6·4х+1= — 1 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Сгруппируем слагаемые следующим образом:
1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image020.png» /> ·9х+1+ 1 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image020.png» /> ·9х·9+ 1 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
31,5= 21· 4 9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
4 9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image032.png» /> х= 3 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image034.png» /> 2х= 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
( 5 ) 2+4+6+. +2 x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image035.png» /> = 5 45 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image036.png» /> , x Î N
Логарифмируя по основанию 5 (обе части уравнения положительны), получим
1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image020.png» /> (2+4+6+. +2x) = 45
Используя формулу суммы первых n членов арифметической прогрессии
Sn =n( a 1 + a n 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x 1+ x 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image038.png» /> =45 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
корни которого x1 = -10 и x2 = 9.
Поскольку x ÎN, остается x = 9.
Неравенства, содержащие переменные в показатели степени, называются показательными. Методы применяемы при решении показательных уравнений, мы также можем использовать и при решении показательных неравенств. Приведем несколько примеров.
2 x — 3 ≥ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image040.png» /> 4+ 1 6- 2 x — 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
В этом неравенстве мы используем метод введения новой переменной.
Пусть 2 x — 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image042.png» /> =t, тогда получаем неравенство
t ≥ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image043.png» /> 4+ 1 6- t <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Преобразуем последнее неравенство
4+ 1 6- t <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image045.png» /> – t ≤ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
t 2 — 10 t +25 6- t ≤ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
(t-5) 2 6-t ≤ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Используя метод интервалов, найдем решение неравенства с переменной
t=5, t > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image049.png» /> 6. Отсюда 2 x — 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image042.png» /> =5 и 2 x — 3 > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Пусть 2 x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image051.png» /> =a, решим уравнение и неравенство с модулем.
Из уравнения a-3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image052.png» /> =5 получаем
a-3=5 a-3=-5 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
a=8 a=-2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Подставим вместо a= 2 x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2 x =8 2 x =-2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Модуль a — 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image052.png» /> есть расстояние на координатной оси от точки a до точки 3.
Для решения неравенств a — 3 > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image056.png» /> 6 необходимо найти такие точки, расстояние от которых до точки 3 больше 6. Справа от точки 3 расположена точка 9 на расстоянии 6 единиц, а слева — точка (-3). Поэтому из неравенства
a — 3 > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image056.png» /> 6 получаем a <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image057.png» /> -3 или a > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2 x 2 x >9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2 x > 2 log 2 9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
x > log 2 9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Ответ: ∪ ( log 2 9 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
2 (3 2x + 2 x ∙ 3 x+1 + 3 0 ) > 3 (4 x — 2 x ∙ 3 x+1 + log 3 2) <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Так как и левая, и правая части неравенства положительны, то от них можно взять log2 :
3 2x + 2 x ∙ 3 x +1> log 2 3 (4 x — 2 x ∙ 3 x+1 + log 3 2) <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
3 2x + 2 x ∙ 3 x +1> (4 x — 2 x ∙ 3 x+1 + log 3 2)∙ log 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
3 2x + 2 x ∙ 3 x +1> (4 x — 2 x ∙ 3 x+1 )∙ log 2 3 +1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
3 2x + 2 x ∙ 3 x > (4 x — 2 x ∙ 3 x+1 )∙ log 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Поделим каждое слагаемое неравенства на ( 2 x ∙ 3 x ) <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
3 2 x +1> 2 3 x — 3 ∙ log 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Обозначим: 3 2 x <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image069.png» /> =y, где y > <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y+1 > 1 y — 3 ∙ log 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Умножим каждое слагаемое на y:
y 2 +y> 1-3y ∙ log 2 3 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Перенесем многочлен из левой стороны в правую сторону:
y 2 +y- 1-3y ∙ log 2 3 >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y 2 +y — log 2 3+3y log 2 3 >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y 2 + 3 log 2 3 +1 y- log 2 3 >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y 2 + 3 log 2 3 +1 y- log 2 3=0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
D = 3 log 2 3 +1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image076.png» /> 2 + <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image077.png» /> 4 log 2 3= 9 log 2 3 2 +10 log 2 3 +1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
D >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y = — 3 log 2 3 +1 ± 9 log 2 3 2 +10 log 2 3 +1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
В связи с тем, что log 2 3 >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
1AppDataLocalTempmsohtmlclip11clip_image081.png» /> , то и D > 3 log 2 3 +1 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Из этого следует, что только один из корней будет больше нуля:
y = — 3 log 2 3 +1 + 9 log 2 3 2 +10 log 2 3 +1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Отметим точку y на оси, y >0 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
y Î — 3 log 2 3 +1 + 9 log 2 3 2 +10 log 2 3 +1 2 ;+∞ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Из этого следует, что x Î log 3 2 — 3 log 2 3 +1 + 9 log 2 3 2 +10 log 2 3 +1 2 ;+∞ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Ответ: x Î log 3 2 — 3 log 2 3 +1 + 9 log 2 3 2 +10 log 2 3 +1 2 ;+∞ <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
— 3 log 2 3 +1 + 9 log 2 3 2 +10 log 2 3 +1 2 <img style="float: left; margin: 0 10px 5px 0;" src="file:///C:UsersWEBMAS
Работа над данным проектом была интересной и увлекательной. Но что самое главное — она стала очень полезной для меня, так как совсем скоро мне предстоит сдавать экзамены. Ведь изучение над этой темой не только дало мне новые знания, но также помогло развить логическое мышление и научило находить решение в, казалось бы, безвыходных ситуациях.
Мне понравилось работать над данной темой, потому что благодаря этому проекту я смогла расширить свои знания в области показательных уравнений и неравенств.
Алгебра и начала математического анализа 10-11 класс:/ Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачев, Н.Е.Федоров, М.И.Шабунин
Алгебра и начала математического анализа. 10-11 класс. Учебник. Базовый и углублённый уровни. Колягин Ю. М.
ЕГЭ. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией И.В. Ященко.
ЕГЭ 2016. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией И.В. Ященко.
- Показательные уравнения и неравенства
- Показательная функция
- Что такое показательная функция?
- Решение показательных неравенств
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- 💡 Видео
Видео:Показательные уравнения. 11 класс.Скачать
Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
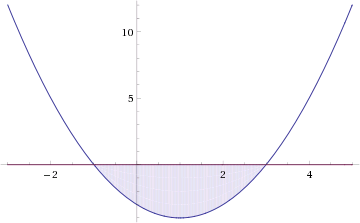
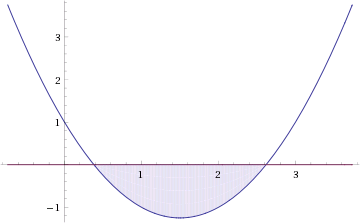
Это означает, что данное уравнение имеет два корня. Находим их:
Переходя к обратной подстановке, получаем:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0. Пример 4. Решите уравнение:
Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение:
Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
Ответ: x = 2. Видео:Это просто! Как решать Показательные Неравенства?Скачать  Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится:
Тогда неравенство примет вид:
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t:
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9. Решите неравенство:
Решение:
Делим обе части неравенства на выражение:
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
Воспользуемся заменой переменной:
Исходное уравнение тогда принимает вид:
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательный ответ:
Пример 10. Решите неравенство:
Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Видео:11 класс, 13 урок, Показательные неравенстваСкачать  Показательные уравнения и неравенства с примерами решенияСодержание: Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными. Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать  Решении показательных уравненийПри решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции. Пусть Каждому значению показательной функции Пример:
Решение: Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение: а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ: При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней. Пример:
Решение: а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. б) Разделив обе части уравнения на Ответ: При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной. Пример: Решить уравнение Решение: Обозначим Таким образом, из данного уравнения получаем
откуда находим: Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной. Пример: Решить уравнение Решение: Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14). Пример: Решить уравнение Решение:
Пример: При каком значении а корнем уравнения Решение: Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при Показательные уравнения и их системыПоказательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений. 1 Приведение к одному основанию. Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду Пример №1Решите уравнение Решение: Заметим, что
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1. Пример №2Решить уравнение Решение: Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем Последнее уравнение равносильно уравнению 4х-19 = 2,5х. 2 Введение новой переменной. Пример №3Решить уравнение Решение: Применив тождество 2, перепишем уравнение как Введем новую переменную: которое имеет корни Пример №4Решить уравнение Решение: Разделив обе части уравнения на
последнее уравнение запишется так: Решая уравнение, найдем Значение
Пример №5Решить уравнение Решение: Заметим что Перепишем уравнение в виде Обозначим Получим Корнями данного уравнения будут Следовательно, III Вынесение общего множителя за скобку. Пример №6Решить уравнение Решение: После вынесения за скобку в левой части
Системы простейших показательных уравненийПример №7Решите систему уравнений: Решение: По свойству степеней система уравнений равносильна следующей системе : Очевидно, что последняя система имеет решение Пример №8Решите систему уравнений: Решение: По свойству степеней система уравнений равносильна следующей системе: Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем
Пример №9Решите систему уравнений: Решение: Сделаем замену: Очевидно, что эта система уравнений имеет решение Тогда получим уравнения
Приближенное решение уравненийПусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения Оказывается, что для корня Пример №10Найдите интервал, содержащий корень уравнения Решение: Поделив обе части уравнения на 2 , получим, Так как, для нового уравнения Значит, в интервале,
Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0). Нахождение приближенного корня с заданной точностьюИсходя из вышесказанного, заключаем, что если выполнено неравенство
корень уравнения с точностью Пример №11Найдите приближенное значение корня уравнения Решение: Из предыдущего примера нам известно, что корень лежит в интервале (-1; 0). Из того, что Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если Пусть Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0 При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 💡 ВидеоПоказательные неравенства. 11 класс.Скачать  11 класс, 12 урок, Показательные уравненияСкачать  Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать  Показательные неравенства и их системы. Вебинар | МатематикаСкачать  Графический метод решения показательных уравнений и неравенств Алгебра 10 (база)Скачать  Показательные уравнения и неравенстваСкачать  Как решать Показательные Уравнения? (часть 2)Скачать  Как решать системы показательных уравнений. Урок№ 27Скачать  10 класс. Алгебра. Системы показательных уравнений.Скачать  ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ😩 #математика #shorts #егэ #огэ #уравнение #показательныеуравненияСкачать  Показательные неравенства за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать  Методы решения показательных уравнений. Урок №25.Скачать  Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать  Показательные уравнения — что это такое и как решатьСкачать  Показательные уравнения | Алгебра 11 класс #8 | ИнфоурокСкачать  |
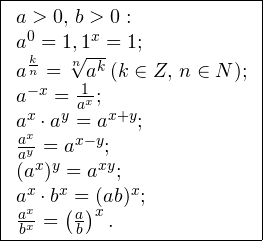0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n]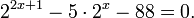 
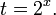
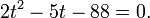
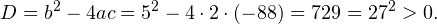0. ]» title=»Rendered by QuickLaTeX.com»/>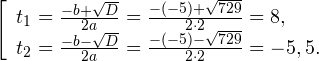
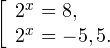
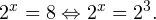
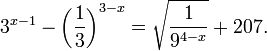
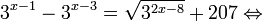
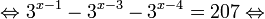
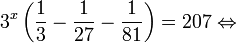
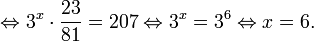
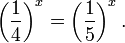
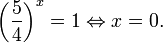
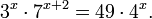
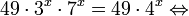
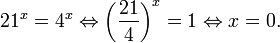
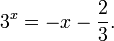
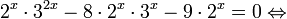
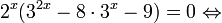
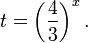
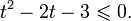
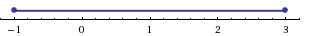
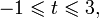
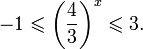
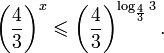
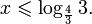
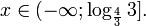
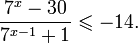
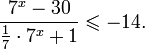
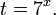
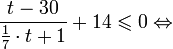
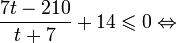
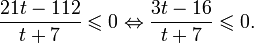
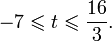
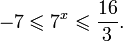
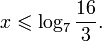
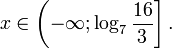
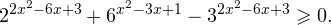
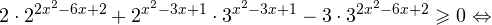
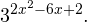
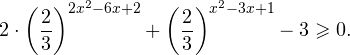
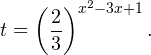
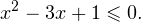
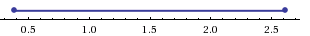
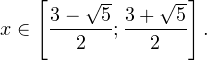
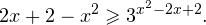
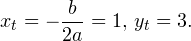
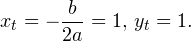
соответствует единственный показатель s.
откуда находим 
получим уравнение 
равносильное данному. Решив его, получим 
тогда 
является число, равное 2?
. Отсюда 
и перепишем наше уравнение в виде
Получим уравнение 
Однако корень
не удовлетворяет условию 
Значит, 
получим:
не удовлетворяет условию 
Следовательно,
Значит 
Получим 
, а в правой 
, получим 
Разделим обе части уравнения на 
получим 
Отсюда получим систему 
Последняя система, в свою очередь, равносильна системе: 
Подставив полученное значение во второе уравнение, получим 
Тогда наша система примет вид: 
. Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое 
(читается как «кси»), что 
содержащий лишь один корень уравнения .
выражения f(х) в точке 
(левый конец отрезка переходит в середину);
вычисляются значения 
данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые 
и 
удовлетворяющие неравенству 
уравнение имеет хотя бы один корень. В то же время уравнение при 
не имеет ни одного корня, так как,
выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим 
Для 
проверим выполнение условия
корень уравнения принадлежит интервалу
Пусть
Если 
приближенный
. Если 
то корень лежит в интервале 
если 
то корень лежит в интервале 
. Продолжим процесс до нахождения приближенного значения корня с заданной точностью.
с заданной точностью
заключаем, что корень лежит в интервале (-0,5; 0).
