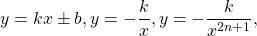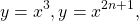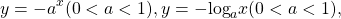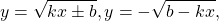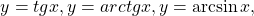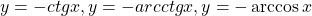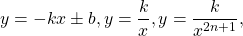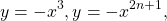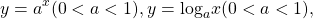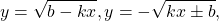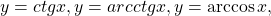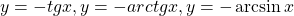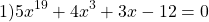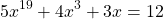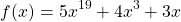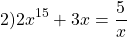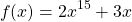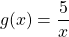Докажите что уравнение имеет один корень на промежутке

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

Докажите что уравнение имеет один корень на промежутке

Определение 1. Пусть функция определена в некоторой окрестности точки . Придавая независимой переменной приращение х , невыводящее за пределы окрестности, получим новое значение + х , также принадлежащее окрестности . Тогда значение функции заменится новым значением , то есть получит приращение

Если существует предел отношения приращении функции у к вызвавшему его приращению независимой переменной х при стремлении х к 0, т.е. , то он называется производной функции в точке х и обозначается .

Операция вычисления производной называется операцией дифференцирования.

Образно говоря, равенство означает, что производная функции в точке х равна скорости изменения переменной у относительно переменой в указанной точке.

Определение 2. Функция , заданная в некоторой окрестности точки R называется дифференцируемой в этой точке, если ее приращение , представимо в этой окрестности в виде , где — постоянная, О( х) — бесконечно малая более высокого порядка, чем х.

Линейная функция (аргумента х ) называется дифференциалом функции в точке х и обозначается df(x или dy .

Таким образом, у = dy + О( х) , .

Можно доказать следующую теорему:

Теорема 1. Функция дифференцируема в некоторой точке в том и только том случае, когда в этой точке имеет конечную производную.

Учитывая определение 2 и утверждение теоремы, в качестве определения дифференцируемой функции может быть принято следующее:

Определение 3. Если функция у имеет производную в точке , то говорят, что при данном значении функция дифференцируема.

То есть существование производной функции в точке х равносильно ее дифференцируемости в этой точке.

Теорема 2 . Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.

Обратная теорема не верна: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в этой точке.

Если функция определена в некоторой окрестности точки , принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х производную, то эта производная равна нулю.

1) непрерывна на отрезке [ ]

2) имеет в каждой точке интервала конечную производную,

3) принимает равные значения на концах отрезка [ ], то есть f(a) = f(b) , то существует, по крайней мере, одна такая точка , что .

Если функция непрерывна на отрезке [ ] и в каждой точке интервала имеет конечную или определенного знака бесконечную производную, то существует такая точка , что f(b) — f(a) = f ( (b — a).

Используя теорему Лагранжа, можно доказать следующие теоремы:

Условие постоянства функции

Теорема 3. (Условие постоянства функции) Пусть функция определена и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную производную . Для того, чтобы была на указанном отрезке постоянной, необходимое и достаточное условие внутри Х.

Если две функции и определены и непрерывны в промежутке Х и внутри него имеют конечные производные и , причем (внутри Х), то эти функции на всем промежутке Х отличаются лишь на постоянную: (C = const).

Теорема 4. (Признак монотонности функций)

Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна).

Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает) на этом интервале.

Если функции и непрерывны на отрезке [ ] и в каждой точке интервала имеют конечные производные , , причем для , а f(а) g(а) , тогда для любой точки выполняется неравенство .

На основании утверждения теоремы 5 для того, чтобы доказать неравенство f(x) 0 при х 0 , достаточно доказать, что f(0) 0 и (х) 0 при х 0 . А для того, чтобы доказать неравенство при , можно воспользоваться второй производной и при и т.д.

С помощью производной можно также определить число корней того или иного уравнения. Один из возможных приемов основан на следующей теореме:

Если функция определена и непрерывна на отрезке и во всех его внутренних точках имеет конечную производную, то между любыми двумя корнями этой функции, расположенными на отрезке, имеется хотя бы 1 корень ее производной.

Рассмотренные теоретические положения используются при решении задач.

Задача 1. Докажите тождество 3 arcsin x — arccos( 3 4 ) = , если .

Решение. Рассмотрим функцию 3 arcsinx — arccos( 3 4 на отрезке [ ]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что (т.3)

Если , то следовательно, и . Для определения значения вычислим значение функции в произвольной точке интервала . Пусть , тогда и .

Вычислим значение функции на концах заданного отрезка.

Таким образом, тождество верно при любом .

Задача 2. Найдите сумму .

Решение. Представив искомую сумму в виде , заметим, что .

Используя формулу суммы членов геометрической прогрессии, получим,

Итак, искомая сумма имеет вид .

Используя полученную формулу, можно, например, вычислить

Задача 3. Найдите сумму:

Решение. Используя результат, полученный в примере 2, заметим, что

Задача 4. Решите уравнение:

Решение. Очевидно, что — корень уравнения. Докажем, что уравнение других корней не имеет. Рассмотрим функцию

Для функции точка является точкой минимума, в которой функция принимает наименьшее значение. Значит, для всех , отличных от нуля, > .

Задача 5. Решите уравнение:

Преобразуем уравнение к виду:

Рассмотрим функции и при .

Сравним множества значений этих функций. Очевидно, что .

Найдем с использованием производной.

Функция непрерывна на промежутке и имеет на нем единственную критическую точку , в которой достигает своего наибольшего значения.

Следовательно, решение уравнения находим из решения системы:

Рассмотрим функцию , при .

Функция непрерывна на промежутке и является возрастающей, . — является точкой минимума функции , в которой функция принимает наименьшее значение, ровное нулю. Следовательно, для всех > .

Таким образом, исходное уравнение имеет единственный корень .

Задача 6. Докажите, что уравнение может иметь не более трех различных корней.

Решение. Рассмотрим функцию . Функция является дифференцируемой на R . Предположим, что функция имеет более трех различных корней, например, четыре. Тогда должна иметь не более трех различных корней (т.6), то есть обращается в нуль не менее трех раз.

Функция дифференцируема на R . Ее производная обращается в нуль не менее двух раз. Тогда имеет не менее двух нулей, а ее производная не менее одного нуля. Но функция нулей не имеет. Получили противоречие. Значит, сделанное предположение неверно, функция более трех различных корней иметь не может. Таким образом, заданное уравнение может иметь не более трех различных корней.

Производную можно использовать при доказательстве и решении неравенств.

Задача 7. Доказать, что при 0$»>.

Доказательство. Докажем справедливость следующих неравенств:

0. end —>

Для доказательства неравенства (2) рассмотрим функцию

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

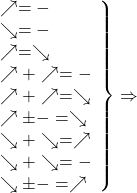
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

1),y = x(a > 1),]» title=»Rendered by QuickLaTeX.com»/>

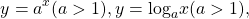
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

1),y = — x(a > 1),]» title=»Rendered by QuickLaTeX.com»/>

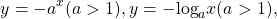
Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Видео:Доказать, что уравнение не имеет положительных корнейСкачать

«Решаем с помощью производной»

Разделы: Математика

Производная широко применяется при решении ряда задач элементарной математики. Из всего круга таких задач выделим те, при решении которых используется теорема Лагранжа и ее следствия. К ним относятся задачи на доказательство тождеств, неравенств, вывод формул тригонометрии, разложение алгебраических выражений на множители, решение уравнений, неравенств, систем уравнений, уравнений с параметрами. При этом можно указать общие методы решения и некоторые частные приемы.

Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что .

Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].

Следствие 2. Если функции и непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.

Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.

Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.

Теорему Лагранжа можно применять:

— при доказательстве неравенств, в частности – числовых неравенств;

— при исследовании вопроса о корнях многочлена или уравнения;

— при решении уравнений.

В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа , c (a;b) и оценивается f’(c), а, следовательно, и выражение , что позволяет доказать рассматриваемое неравенство или решить вопрос о корнях многочлена, уравнения.

Пример 1. Доказать, что .

Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), . Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и , где 0,6 , т.е. . Оценим число . Так как 0,6 2 . Тогда и окончательно .

Пример 2. Доказать, что e x >=ex.

Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=e x -ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b , т.е. . Так как c>1 при b>1, то e c >e и, следовательно, e c -e>0. Тогда , а значит e b -eb>0, т.е. e b >eb для любого b>1. Таким образом доказано, что e x >=ex при x>=1.

Если b , т.е. с c c -e , следует, что e b -eb>0, т.е. e b >eb.

Итак, доказано, что неравенство e x >=ex верно при любом действительном х. В частности, при x=c+1 получим e c+1 >=e(c+1), т.е. e c >=c+1, где с – любое действительное число.

Пример 3. Доказать, что уравнение не имеет действительных положительных корней.

Решение. Пусть b – любое положительное число. Рассмотрим функцию f(x)= , непрерывную на отрезке [a;b] и имеющую производную на интервале (0;b). По теореме Лагранжа имеем , 0 . А так как при любом с>0 e c >c+1 (доказано в примере 2), то e c -c>1 и, следовательно, . Отсюда получим , а значит для любого b>0. Таким образом, при x>0, т.е. , следовательно, равенство не выполняется ни при каком x>0. А, значит, уравнение не имеет действительных положительных корней.

Пример 4. Доказать, что на промежутке (0, 2) имеется не более двух различных действительных корней уравнения .

Решение. Предположим, что уравнение имеет не менее трех различных действительных корней х₁, х₂, х₃, принадлежащих промежутку (0,2), и пусть x₁ , т.е. f(x₁)=f(x₂)=f(x₃)=0. На каждом из отрезков [x₁;x₂], [x₂;x₃] для функции f(x) выполняются условия теоремы Лагранжа, следовательно, существуют числа c₁ и с₂ из интервалов (х₁;х₂), (х₂;х₃) соответственно, такие, что и . А так как f(x₁)=f(x₂)=f(x₃)=0, то f’(c₁)=0 и f’(c₂)=0, причем с₁с₂.

Найдем производную f’(x):

. Так как для любых х, то уравнение f’(x)=0 имеет единственный корень x=, принадлежащий промежутку (0, 2). Пришли к противоречию, так как с₁ и с₂ (с₁с₂) являются корнями уравнения f’(x)=0, тем самым доказано, что уравнение имеет на промежутке (0,2) не более двух различных действительных корней.

Пример 5. Решить уравнение x 9 -9x 5 +63x-55=0.

Решение. Легко заметить, что число х₁=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х₂, отличный от х₁. Числа х₁ и х₂ являются нулями функции f(x)=x 9 -9x 5 +63x-55 и, следовательно, f(x₁)=f(x₂)=0. Применим терему Лагранжа к функции f(x) на отрезке [x₁;x₂], если x₁ x₂. Следовательно, найдется такая внутренняя точка с этого отрезка, что будет выполняться . Учитывая, что f(x₁)=f(x₂)=0, получим f’(с)=0, т.е. число с – корень уравнения f’(x)=0. Но производная f’(x)=9x 8 -45x 4 +63, т.е. f’(x)=9(x 4 -2,5) 2 +6,75 положительна для любых х, а значит уравнение f’(x)=0 не имеет корней. Полученное противоречие доказывает, что найденный корень х₁=1 является единственным корнем уравнения x 9 -9x 5 +63x-55=0.

Определить число критических точек функции y=(x 2 -1)(x 2 -8х)(x-9).

Решение. Так как степень многочлена f(x)= (x 2 -1)(x 2 -8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней. Применим теорему Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках [-1;0], [0;1], [1;8], [8;9] и при этом учтем, что f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся внутренние точки х₁, х₂, х₃, х₄ соответственно, такие, что , , , , т.е. f’(x₁)=0, f’(x₂)=0, f’(x₃)=0, f’(x₄)=0. А учитывая, что x₁, х₂, х₃, х₄ – различные корни многочлена f’(x) четвертой степени, делаем вывод, что других корней, отличных от полученных, нет и, следовательно, функция y=(x 2 -1)(x 2 -8х)(x-9) имеет четыре критические точки.

Условие монотонности функции можно применять:

— при решении неравенств;

— при доказательстве неравенств с переменной;

— при доказательстве числовых неравенств;

— при исследовании вопроса о количестве корней уравнения;

— в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.

Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.

Пример 7. Доказать, что 3xcosx .

Решение. Докажем, что, если 0 , то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке функцию f(x)=tgx-3x+2sinx. Ее производная при принимает положительные значения, следовательно, функция f(x) возрастает на промежутке и на нем f(x)>f(0).

Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0. А так как на промежутке cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано, что sinx+sin2x-3xcosx>0, то есть, что 3xcosx .

Пример 8. Доказать, что

1) и , если 0 и , если e . Так как ее производная равна нулю при х=е, а при 0 0 и f’(x) e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+) — убывает. Тогда для любых значений х₁ и х₂ таких, что 0 . Запишем его в виде , . Учитывая, что функция ln t возрастающая, получим . А если обе части неравенства умножить на произведение x₁x₂>0, то получим x₂lnx₁ , откуда и будем иметь .

Если же e f(x₂), то есть , откуда и получим и .

Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.

Пример 9. Сравнить (сtg48°) tg48° и (сtg50°) tg50° .

Решение. Заметим, что сtg48°=сtg , tg48°=tg , ctg50°=ctg , tg50°=tg , а также, что . Взяв , и учитывая, что , если 0 , т.е. (сtg48°) tg48° > (сtg50°) tg50° .

Пример 10. Доказать, что 2006 2007 >2007 2006 .

Решение. Воспользуемся неравенством x₁ x2 >x₂ x1 , если e 2007 >2007 2006 .

Определить число действительных корней уравнения 2х 3 -24х-19=0.

Решение. Функция f(x)= 2х 3 -24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x 2 -24=6(x-2)(x+2).

При x 2 f’(x)>0, а при –2 0, f(2)=-51 0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х 3 -24х-19=0 имеет три действительных корня, которые находятся на промежутках (-3;-2), (-2;2), (2;5).

Остальные следствия теоремы Лагранжа можно применять:

— при доказательстве тождеств, в частности при выводе формул элементарной математики;

— при упрощении выражений;

— при разложении алгебраических выражений на множители.

При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.е. имеет вид f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x), и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту постоянную находят, положив х равным некоторому значению х₁.

Пример 12. Вывести формулу .

Решение. Функция f(x)= непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin 2 0-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим =0, или .

Пример 13. Доказать, что arctgx=arcsin при x , тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.

, . Так как при x и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin , то есть Итак, получим arctgx=arcsin при x

Решение. Заметим, что , для любого действительного х и функции , непрерывны на всей числовой прямой. Имеем ,

1) Рассмотрим функцию F(x)=f(x)+g(x), x (-;-1) (0;1).

F(x)= , а F’(x)=f’(x)+g’(x)= . Если x (-;-1), то |х 2 -1|=х 2 -1, |х|=-х и F’(x)=0. Если x (0;1), то |х 2 -1|=-(х 2 -1), |х|=х и F’(x)=0. На основании условия постоянства функции F(x)=c, то есть . На каждом из рассматриваемых промежутков определим с, положив, например, х= и x= .

, cледовательно, с=.

, следовательно, с=0. Имеем: при x (-;-1), при x (0;1).

2) Рассмотрим функцию G(x)=f(x)-g(x), x (-1;0) (1; +).

Если x (-1;0), то |х 2 -1|=-(х 2 -1), |x|=-x и G’(x)=0.

Если x (1; +), то |х 2 -1|=х 2 -1, |x|=x и G’(x)=0. Тогда на указанных промежутках функция G(x) постоянна, т.е. . Положим x= и x= , получим , следовательно, с=; , тогда с=0.

Имеем: при x (-1;0), при x (1;+ ).

3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.

f(-1)=arccos(-1)=, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=+g(x), то есть . , , следовательно, при х=0 f(x)=-g(x), то есть . f(1)=arccos1=0, g(1)=arcsin0=0, следовательно, при х= 1 f(x)=g(x), то есть .

Таким образом, данное тождество доказано для всех действительных х.

Пример 15. Разложить на множители выражение

y 2 (x-z)+x 2 (z-y)+z 2 (y-x).

Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y 2 (x-z)+x 2 (z-y)+z 2 (y-x).

f’(x)=y 2 +2x(z-y)-z 2 =y 2 -z 2 -2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).

Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.

g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x 2 ).

Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)((y+z)x-x 2 )+c. Найдем с, полагая в этом равенстве, например, х=0. Имеем yz 2 -zy 2 =c. Тогда f(x)=g(x)+yz 2 -zy 2 , то есть

f(x)=(y-z)((y+z)x-x 2 )+yz 2 -zy 2 =(y-z)(xy+xz-x 2 )-yz(y-z)=(y-z)(xy-x 2 +xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).

Итак, y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)(y-x)(x-z).

🌟 Видео

Уравнение, в котором ошибётся каждый второйСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Быстрый способ решения квадратного уравненияСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Как решить уравнение с квадратом #алгебра #квадрат #уравнение #кореньСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

При каких значениях параметра уравнение имеет единственный кореньСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Вариант 39, № 2. Линейное уравнение, имеющее бесконечно много корнейСкачать

Как решить уравнение с корнями Линейное уравнение Простое уравнение Как решать корниСкачать

6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Найдите все значения а при каждом из которых уравнение имеет ровно один корень на отрезкеСкачать

Решить уравнение. #ShortsСкачать