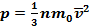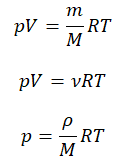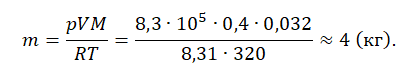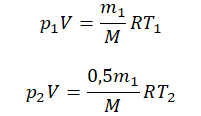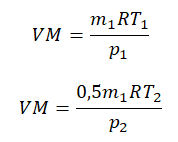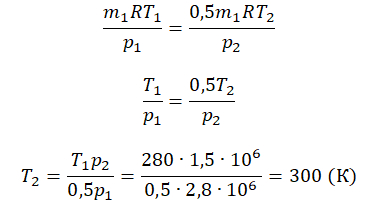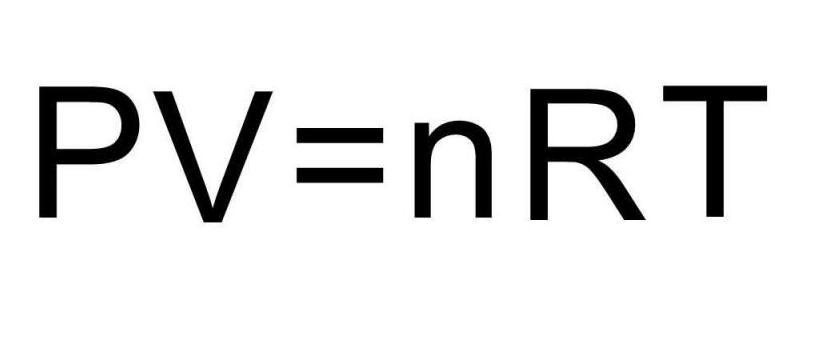Идеальный газ – это модель реального газа. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами. Точнее, Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало ⇒ Eк >> Eр .
Основное уравнение МКТ связывает макроскопические параметры (давление p, объём V, температура T, масса m) газовой системы с микроскопическими параметрами (масса молекулы , средняя скорость их движения):
, где n— концентрация, 1/м 3 ; m — масса молекулы, кг; 
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением , объёмом и абсолютной температурой идеального газа, характеризующее состояние данной системы газа. 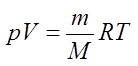
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества ν=const. Тогда:
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: 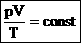
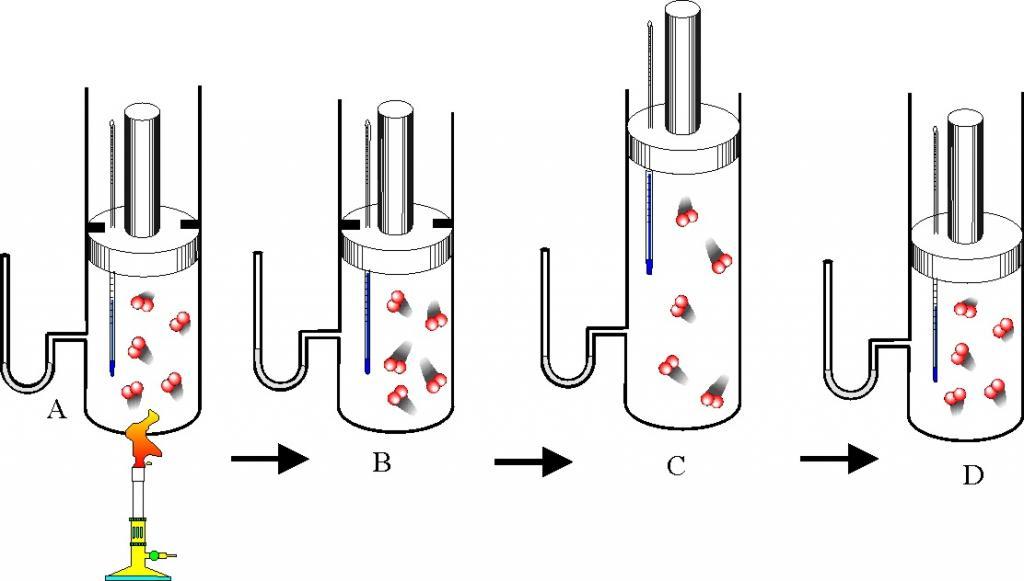
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:
Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.

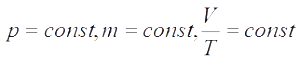
Изохорный п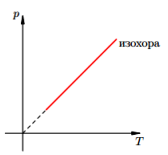
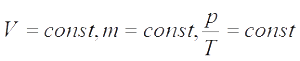
Вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
- Уравнение состояния идеального газа
- теория по физике 🧲 молекулярная физика, МКТ, газовые законы
- Уравнение состояния идеального газа и смысл абсолютной температуры
- Газовое состояние вещества
- Идеальный газ
- Закон Клапейрона-Менделеева
- Другие формы записи уравнения
- Закон Бойля-Мариотта
- Законы Шарля и Гей-Люссака
- Абсолютная температура
- Принцип Авогадро и газовые смеси
- Пример решения задачи
- 🎥 Видео
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | 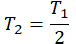 |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | 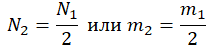 |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | 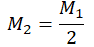 |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙10 6 Па
1,5 МПа = 1,5∙10 6 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
Преобразим уравнения и получим:
Приравняем правые части и выразим искомую величину:

Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа и смысл абсолютной температуры
Каждый человек в течение своей жизни сталкивается с телами, которые находятся в одном из трех агрегатных состояний вещества. Самым простым для изучения агрегатным состоянием является газ. В статье рассмотрим концепцию идеального газа, приведем уравнение состояния системы, а также уделим некоторое внимание описанию абсолютной температуры.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Газовое состояние вещества
Каждый школьник хорошо представляет, о каком состоянии материи идет речь, когда слышит слово «газ». Под этим словом понимают тело, которое способно занимать любой предоставленный ему объем. Оно не способно сохранять форму, поскольку не может сопротивляться даже самому незначительному внешнему воздействию. Также газ не сохраняет и объем, что его отличает не только от твердых тел, но и от жидкостей.

Как и жидкость, газ является текучей субстанцией. В процессе движения твердых тел в газах последние препятствуют этому движению. Появившуюся силу называют сопротивлением. Ее величина зависит от скорости движения тела в газе.
Яркими примерами газов является воздух, природный газ, который используется для отопления домов и приготовления пищи, инертные газы (Ne, Ar), которыми заполняют рекламные трубки тлеющего разряда, или которые используют для создания инертной (неагрессивной, защитной) среды при сварке.
Видео:Уравнение состояния идеального газаСкачать

Идеальный газ

Прежде чем переходить к описанию газовых законов и уравнения состояния, следует хорошо разобраться с вопросом, что собой представляет идеальный газ. Это понятие вводится в молекулярно-кинетической теории (МКТ). Идеальным называется любой газ, который удовлетворяет следующим характеристикам:
- Образующие его частицы не взаимодействуют друг с другом за исключением непосредственных механических столкновений.
- В результате столкновения частиц со стенками сосуда или между собой их кинетическая энергия и количество движения сохраняются, то есть столкновение считается абсолютно упругим.
- Частицы не имеют размеров, но обладают конечной массой, то есть подобны материальным точкам.
Естественно, что любой газ является не идеальным, а реальным. Тем не менее, для решения многих практических задач указанные приближения являются вполне справедливыми и ими можно пользоваться. Существует общее эмпирическое правило, которое гласит: независимо от химической природы, если газ имеет температуру выше комнатной и давление порядка атмосферного или ниже, то его с высокой точностью можно считать идеальным и применять для его описания формулу уравнения состояния идеального газа.
Видео:Уравнение состояния идеального газаСкачать

Закон Клапейрона-Менделеева
Переходами между различными агрегатными состояниями вещества и процессами в рамках одного агрегатного состояния занимается термодинамика. Давление, температура и объем являются тремя величинами, которые однозначно определяют любое состояние термодинамической системы. Формула уравнения состояния идеального газа объединяет в единое равенство все три указанные величины. Запишем эту формулу:
Здесь P, V, T — давление, объем, температура, соответственно. Величина n — это количество вещества в молях, а символом R обозначена универсальная постоянная газов. Это равенство показывает, что чем больше произведение давления на объем, тем больше должно быть произведение количества вещества на температуру.
Формула уравнения состояния газа называется законом Клапейрона-Менделеева. В 1834 году французский ученый Эмиль Клапейрон, обобщив экспериментальные результаты его предшественников, пришел к этому уравнению. Однако Клапейрон пользовался рядом констант, которые Менделеев впоследствии заменил одной — универсальной газовой постоянной R (8,314 Дж/(моль*К)). Поэтому в современной физике это уравнение названо по фамилиям французского и русского ученых.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Другие формы записи уравнения
Выше мы записали уравнение состояния идеального газа Менделеева-Клапейрона в общепринятом и удобном виде. Однако в задачах по термодинамике часто может потребоваться несколько иной вид. Ниже записаны еще три формулы, которые непосредственно следуют из записанного уравнения:
Эти три уравнения также являются универсальными для идеального газа, только в них появляются такие величины, как масса m, молярная масса M, плотность ρ и число частиц N, которые составляет систему. Символом kB здесь обозначена постоянная Больцмана (1,38*10-23 Дж/К).
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Закон Бойля-Мариотта
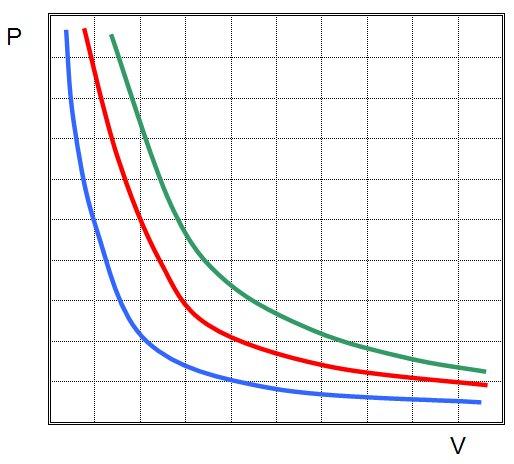
Когда Клапейрон составлял свое уравнение, то он основывался на газовых законах, которые были открыты экспериментально несколько десятилетий ранее. Одним из них является закон Бойля-Мариотта. Он отражает изотермический процесс в закрытой системе, в результате которого изменяются такие макроскопические параметры, как давление и объем. Если положить T и n постоянными в уравнении состояния идеального газа, газовый закон тогда примет вид:
Это и есть закон Бойля-Мариотта, который говорит о том, что произведение давление на объем сохраняется во время произвольного изотермического процесса. При этом сами величины P и V изменяются.
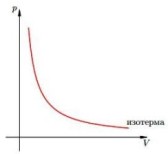
Если изображать график зависимости P(V) или V(P), то изотермы будут представлять собой гиперболы.
Видео:идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Законы Шарля и Гей-Люссака
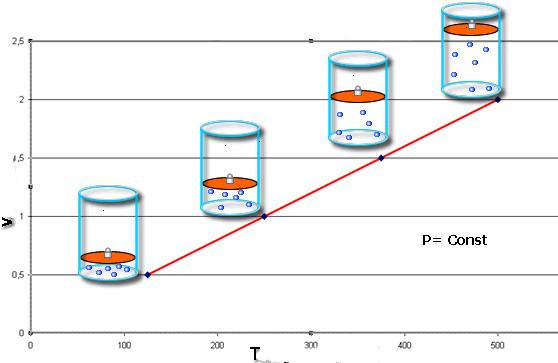
Эти законы математически описывают изобарный и изохорный процессы, то есть такие переходы между состояниями газовой системы, при которых сохраняются давление и объем, соответственно. Закон Шарля математически можно записать следующим образом:
V/T = const при n, P = const.
Закон Гей-Люссака записывается так:
P/T = const при n, V = const.
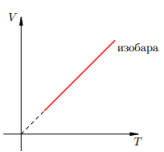
Если оба равенства представить в виде графика, то мы получим прямые линии, которые под некоторым углом наклонены к оси абсцисс. Такой вид графиков говорит о прямой пропорциональности между объемом и температурой при постоянном давлении и между давлением и температурой при постоянном объеме.
Отметим, что все три рассмотренных газовых закона не принимают во внимание химический состав газа, а также изменение его количества вещества.
Видео:Связь между давлением, объёмом и температурой газаСкачать

Абсолютная температура
В быту мы привыкли пользоваться температурной шкалой Цельсия, поскольку она является удобной для описания окружающих нас процессов. Так, вода кипит при температуре 100 oC, а замерзает при 0 oC. В физике эта шкала оказывается неудобной, поэтому применяют так называемую абсолютную шкалу температур, которая была введена лордом Кельвином в середине XIX века. В соответствии с этой шкалой температура измеряется в Кельвинах (К).
Считается, что при температуре -273,15 oC не существует никаких тепловых колебаний атомов и молекул, прекращается полностью их поступательное движение. Этой температуре в градусах Цельсия соответствует абсолютный ноль в Кельвинах (0 К). Из этого определения следует физический смысл абсолютной температуры: она является мерой кинетической энергии составляющих материю частиц, например, атомов или молекул.
Помимо приведенного выше физического смысла абсолютной температуры, существуют другие подходы к пониманию этой величины. Одним из них является упомянутый газовый закон Шарля. Запишем его в следующей форме:
Последнее равенство говорит о том, что при определенном количестве вещества в системе (например, 1 моль) и определенном давлении (например, 1 Па) объем газа однозначно определяет абсолютную температуру. Иными словами, возрастание объема газа при указанных условиях возможно только за счет увеличения температуры, а уменьшение объема свидетельствует об уменьшении величины T.
Напомним, что в отличие от температуры по шкале Цельсия, абсолютная температура не может принимать отрицательные значения.
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

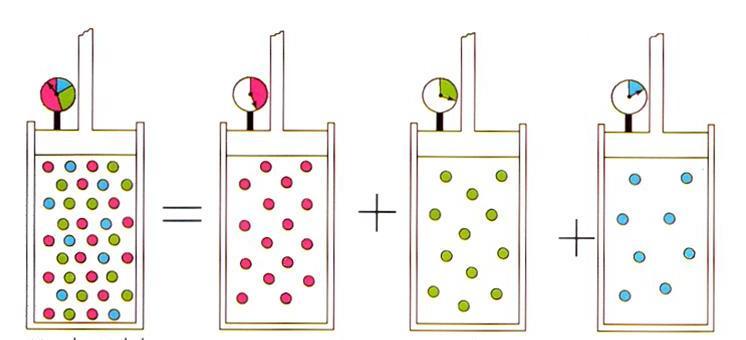
Принцип Авогадро и газовые смеси
Помимо изложенных выше газовых законов, уравнение состояния для идеального газа также приводит к открытому Амедео Авогадро в начале XIX века принципу, который носит его фамилию. Этот принцип устанавливает, что объем любого газа при постоянных давлении и температуре определяется количеством вещества в системе. Соответствующая формула выглядит так:
n/V = const при P, T = const.
Записанное выражение приводит к известному в физике идеальных газов закону Дальтона для газовых смесей. Этот закон гласит, что парциальное давление газа в смеси однозначно определяется его атомной долей.
Видео:ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Пример решения задачи
В закрытом сосуде с жесткими стенками, содержащем идеальный газ, в результате нагревания давление увеличилось в 3 раза. Необходимо определить конечную температуру системы, если ее начальное значение было равно 25 oC.
Сначала переведем температуру из градусов Цельсия в Кельвины, имеем:
T = 25 + 273,15 = 298,15 К.
Поскольку стенки сосуда являются жесткими, то процесс нагревания можно считать изохорным. Для этого случая применим закон Гей-Люссака, имеем:
Таким образом, конечная температура определяется из произведения отношения давлений и начальной температуры. Подставляя в равенство данные, получаем ответ: T2 = 894,45 К. Эта температура соответствует 621,3 oC.
🎥 Видео
Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Уравнение состояния идеального газа. Газовые законыСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

МКТ идеального газа. Уравнения состояния идеального газа | Физика, онлайн-форумСкачать

10 класс урок №39 Уравнение состояния идеального газаСкачать