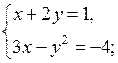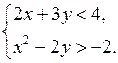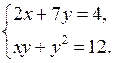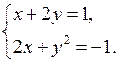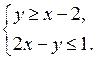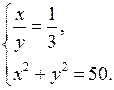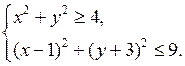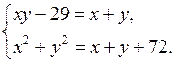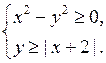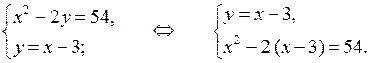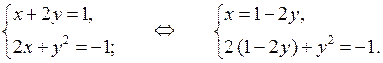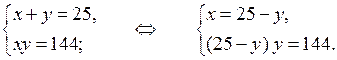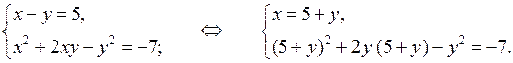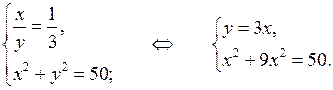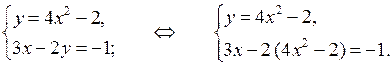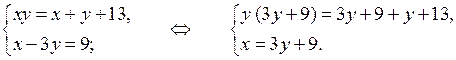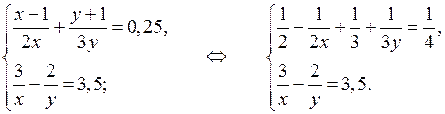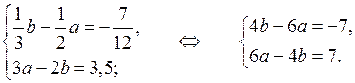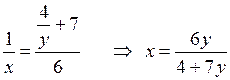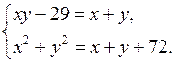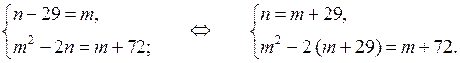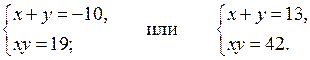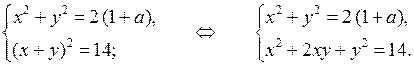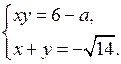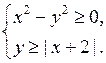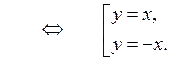Докажите что пара чисел 5 2 не является решением системы уравнений (4 видео)

Докажите что пара чисел 5 2 не является решением системы уравнений

Вопрос по математике:

Докажите, что пара числе (-5;2) не является решением системы уравнений
2x+7y=4
xy+y^2=12

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Школе NET
Register
Login
Newsletter
Мари Умняшка
Докажите, что пара числе (-5;2) не является решением системы уравнений 2x+7y=4 xy+y^2=12
Лучший ответ:
Таня Масян
Урок в 9 классе «Уравнения и неравенства с двумя переменными»
🎥 Видео

Ответы и объяснения 1

Подставим это решение в оба уравнения и сравним результаты

хотя исходное решение удовлетворяет 1-му уравнению, оно не удовлетворяет второму, значит это решение не является решением системы

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Школе NET

Register

Do you already have an account? Login

Don’t you have an account yet? Register

Submit to our newsletter to receive exclusive stories delivered to you inbox!

Главная 
Вопросы & Ответы 
Вопрос 802802

Мари Умняшка

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Докажите, что пара числе (-5;2) не является решением системы уравнений 2x+7y=4 xy+y^2=12

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Лучший ответ:

Таня Масян

Подставим это решение в оба уравнения и сравним результаты

Видео:Не сдал ОГЭ Устное Собеседование shorts #shortsСкачать

Урок в 9 классе «Уравнения и неравенства с двумя переменными»

У р о к
Итоговый урок по теме «Уравнения
и неравенства с двумя переменными»

Цели: обобщить и систематизировать знания учащихся по данной теме; закрепить умения решать уравнения, неравенства и их системы с двумя переменными.

I. Организационный момент.

II. Устная работа.

Какие из пар чисел (0; 3), (1; –2), (–1; 1) являются решениями данных систем?

а) 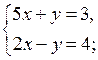в)

б) 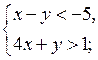г)

III. Формирование умений и навыков.

Предложить учащимся карточки-задания разного уровня сложности. Учащиеся выполняют решения самостоятельно, а учитель осуществляет контроль и в случае необходимости дает им консультации.

К а р т о ч к а № 1

1. Докажите, что пара чисел (–5; 2) не является решением системы уравнений

2. Решите систему уравнений:

а) 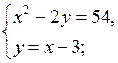б)

3. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.

4. Изобразите на координатной плоскости множество решений системы неравенств:

а) 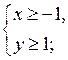б)

К а р т о ч к а № 2

1. Решите систему уравнений:

а) 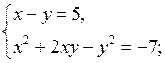б)

2. Не выполняя построения, найдите координаты точек пересечения параболы у = 4х 2 – 2 и прямой 3х – 2у = –1.

3. Произведение двух чисел на 13 больше их суммы. Если из первого числа вычесть утроенное второе число, то получится 9. Найдите эти числа.

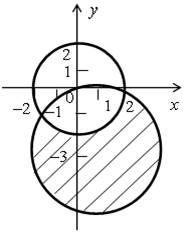
4. Изобразите на координатной плоскости множество решений системы неравенств:

а) 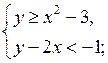б)

К а р т о ч к а № 3*

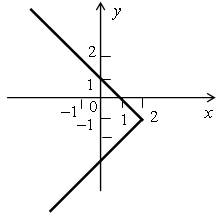
1. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению | у + 1 | = 2 – х.

2. Решите систему уравнений:

а) 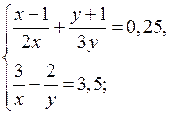б)

3. При смешивании первого раствора кислоты, концентрация которого 20 %, и второго раствора этой же кислоты, концентрация которого 50 %, получили раствор, содержащий 30 % кислоты. В каком отношении были взяты первый и второй растворы?

4. При каких значения параметра а система уравнений:

имеет два решения?

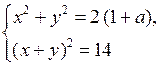
5. Изобразите на координатной плоскости множество решений системы неравенств:

Р е ш е н и е заданий карточки № 1

1. Подставим х = –5 и у = 2 в каждое из уравнений системы:

Значит, пара чисел (–5; 2) не является решением данной системы.

а)

х ₁ = –6 у₁ = –6 – 3 = –9;

х ₂ = 8 у₂ = 8 – 3 = 5.

О т в е т: (–6; –9), (8; 5).

б)

у ₁ = 1 х₁ = 1 – 2 · 1 = –1;

у ₂ = 3 х₂ = 1 – 2 · 3 = –5.

О т в е т: (–1; 1), (–5; 3).

3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:

D = 625 – 4 · 144 = 49;

у ₁ = 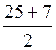= 16 х₁ = 25 – 16 = 9;

у ₂ = 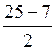= 9 х₂ = 25 – 9 = 16.

О т в е т: 9 и 16.

а) 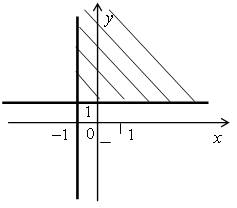б)

Р е ш е н и е заданий карточки № 2

1. а)

у ₁ = –2 х₁ = 5 + (–2) = 3;

у ₂ = –8 х₂ = 5 + (–8) = –3.

О т в е т: (3; –2), (–3; –8).

б)

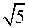
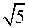
х ₁ = у₁ = 3;

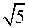
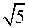
х ₂ = – у₂ = –3.

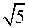
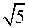
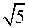
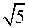
О т в е т: (; 3), (–; –3).

2. Чтобы найти координаты точек пересечения данных параболы и прямой, нужно решить систему уравнений:

х ₁ = 1 у₁ = 4 · 1 – 2 = 2;

х ₂ = у₂ = 4 · – 2 = .

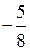
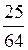
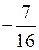
О т в е т: (1; 2), .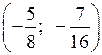

3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:

D = 25 + 264 = 289;

у ₁ = 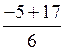= 2 х₁ = 3 · 2 + 9 = 15;

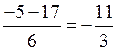
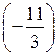
у ₂ = х₂ = 3 · + 9 = –2.

О т в е т: (15; 2), .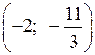

а) 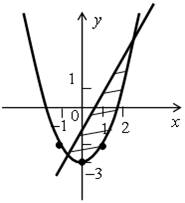б)

Р е ш е н и е заданий карточки № 3*

1. Раскрывая модуль, получим совокупность двух уравнений:

1) если у ≥ –1, то у + 1 = 2 – х,

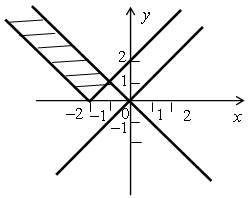
Изобразим на координатной плоскости оба этих случая:

а)

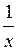
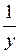
Сделаем замену: = а, = b. Получим систему:

Складывая почленно левые и правые части уравнений этой системы, получим равенство:

Значит, система имеет бесконечное множество решений.

Выразим из второго уравнения переменную а через переменную b:

a = .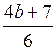

Возвращаясь к замене, получим:

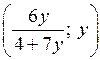
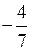
Получаем, что исходная система имеет бесконечное множество решений вида , где у ≠ 0 и у ≠ .

Например, это могут быть такие пары, как 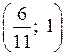, (2; –1), (1,2; –2). И т. д.

б)

Обозначим х + у = т, а ху = п. Тогда имеем:

т ₁ = –10 п₁ = –10 + 29 = 19;

т ₂ = 13 п₂ = 13 + 29 = 42.

Возвращаясь к замене, получим системы:

Решая эти системы, получаем ответ.

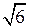
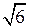
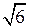
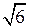
О т в е т: (6; 7), (7; 6), (–5 + ; –5 – ), (–5 – ; –5 + ).

3. Пусть было взято x г первого раствора и y г – второго раствора. По условию в первом растворе было 0,2x г кислоты, а во втором – 0,5y г кислоты.

После смешивания получили 30 %-ный раствор, то есть в нем было 0,3 (x + y) г кислоты. Масса кислоты после смешивания двух растворов равна сумме масс исходных растворов.

Получаем, что первый и второй растворы были взяты в отношении 2 : 1.

Вычтем почленно из второго уравнения системы первое:

Тогда данную систему уравнений можно представить как совокупность двух систем:

1) 2)

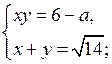
Исходная система будет иметь два решения в трех случаях:

– если каждая из систем имеет по одному решению;

– если первая система имеет два решения, а вторая – решений не имеет;

– если вторая система имеет два решения, а первая – решений не имеет.

Если в каждой из полученных систем выразить одну переменную через другую и найти дискриминант, то в обоих случаях получим:

Выражение 4а – 10 не может быть одновременно больше и меньше нуля, поэтому подходит тот случай, когда каждая из систем имеет единственное решение, то есть, когда D = 0: