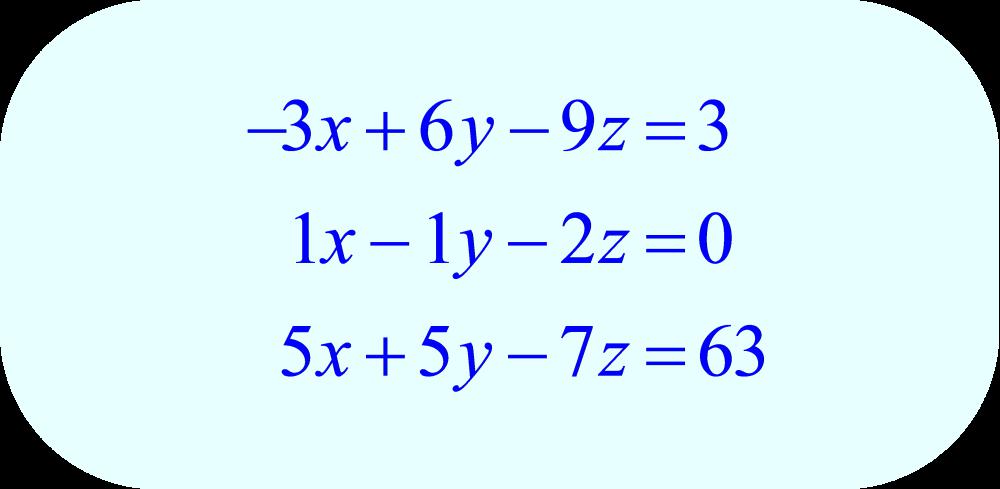Доказать что уравнение 3 степени не имеет корней

Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.

Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0

Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что

x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0

Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.

Найти корни кубического уравнения 2 x 3 — 3 = 0 .

Решение

Необходимо найти х из уравнения. Запишем:

2 x 3 — 3 = 0 x 3 — 3 2 = 0

Необходимо применить формулу сокращенного умножения. Тогда получим, что

x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0

Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.

Ответ: x = 3 3 2 6 .

Видео:Доказать, что многочлен не может иметь целых корнейСкачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0

Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что

A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A

Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.

Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .

Решение

Уравнение является возвратным. Необходимо произвести группировку. Получим, что

5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0

Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :

5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10

Ответ:

x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение кубических уравнений с рациональными корнями

Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .

Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .

Решение

3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0

Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что

D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.

Ответ: х = 0 .

Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :

A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2

Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что

2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0

Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:

± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36

Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида

1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0

Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .

Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:

2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9

После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.

Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .

Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.

Видео:7 класс. Учебник Макарычев. N526a. Докажите, что не имеет корней уравнение. а)х^2+1=0Скачать

Решение кубических уравнений по формуле Кардано

Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .

После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .

Полученные p и q в формулу Кардано. Получим, что

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3

Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .

Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .

Отсюда следует, что

p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108

Производим подстановку в формулу Кордано и получим

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3

— 343 216 3 имеет три значения. Рассмотрим их ниже.

— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2

Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2

Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6

Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2

Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .

Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .

Преобразуем при помощи формулы Кордано:

y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6

x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3

Ответ: x 1 = — 1 2 , x 2 , 3 = 3

При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

«Решение уравнений высших степеней». 9-й класс

Разделы: Математика

Класс: 9

Учебная:

Развивающая:

1. Развитие внимания учащихся.
2. Развитие умения добиваться результатов труда.
3. Развитие интереса к изучению алгебры и навыков самостоятельной работы.

Воспитывающая:

Оборудование: компьютер, проектор.

1 этап работы. Организационный момент.

2 этап работы. Мотивация и выход на постановку проблемы

Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.

В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.

А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.

3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.

1) Решение линейного уравнения.

Линейным называется уравнение вида , где по определению. Такое уравнение имеет единственный корень .

2) Решение квадратного уравнения.

Квадратным называется уравнение вида , где . Количество корней и сами корни определяются дискриминантом уравнения . Для уравнение корней не имеет, для имеет один корень (два одинаковых корня)

, для имеет два различных корня .

Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение -й степени имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена на множители или с использованием замены переменной.

3) Решение кубического уравнения.

Решим кубическое уравнение

Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:

Итак, данное кубическое уравнение имеет три корня: ; ;.

4) Решение биквадратного уравнения.

Очень распространены биквадратные уравнения, которые имеют вид (т.е. уравнения, квадратные относительно ). Для их решения вводят новую переменную .

Решим биквадратное уравнение .

Введём новую переменную и получим квадратное уравнение , корнями которого являются числа и 4.

Вернёмся к старой переменной и получим два простейших квадратных уравнения:

(корни и )

(корни и )

Итак, данное биквадратное уравнение имеет четыре корня:

; ;.

Попробуем решить уравнение используя выше изложенные приёмы.

4 этап работы. Привести некоторые утверждения о корнях многочлена вида , где многочлен n-й степени

Приведём некоторые утверждения о корнях многочлена вида :

1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.

2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.

3) Если на концах отрезка значения многочлена имеют разные знаки (т.е. ,), то на интервале находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.

4) Если число является корнем многочлена вида , то этот многочлен можно представить в виде произведения , где многочлен (-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен . Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).

5) Если уравнение со всеми целыми коэффициентами (причём свободный член ) имеет целый корень , то этот корень является делителем свободного члена . Такое утверждение позволяет подобрать целый корень многочлена (если он есть).

5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.

Пример 1. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: . Проверка показывает, что корнем уравнения является число -1. Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы фактически разложили левую часть уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:

Итак, данное уравнение имеет три корня:

Пример 2. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть уравнения на множители:

Аналогичным образом поступим и с многочленом .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде

произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть исходного уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:

Итак, данное уравнение имеет четыре корня:

6 этап работы. Закрепление изученного материала.

Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.

7 этап работы. Вывод урока.

Решить уравнения высших степеней можно следующим образом:

• используя формулы для нахождения корней (если они известны);
• используя замену переменной;
• раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.

8 этап работы. Домашнее задание.

Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).

Видео:КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Какое уравнение не имеет корней? Примеры уравнений

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Видео:Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

Видео:Решение уравнения третьей степени x³-9x-12=0Скачать

1. Линейное уравнение

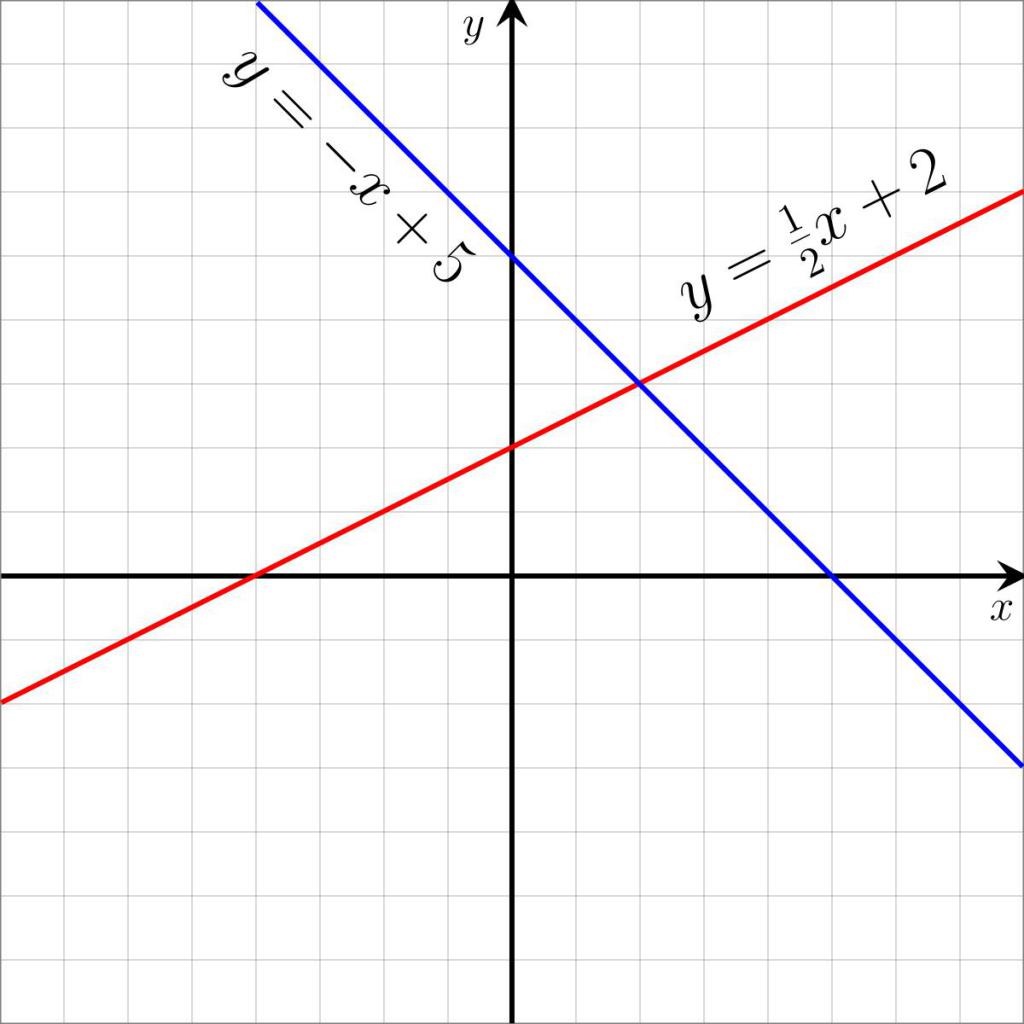
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

Видео:Рациональные корни многочлена с целым показателем. 10 класс.Скачать

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

Видео:Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

3. Тригонометрические уравнения

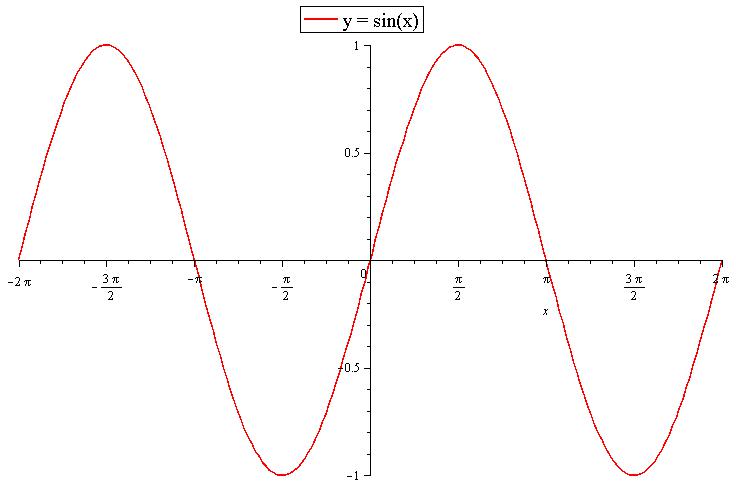
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Видео:Формула Кардано. Решение уравнений третьей степени.Скачать

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

📸 Видео

Докажите, что уравнение не имеет положительных корней. №528 алгебра 7 класс МакарычевСкачать

ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Самый простой способ решить кубическое уравнениеСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Ещё один приём решения иррациональных уравнений с корнем третьей степениСкачать

11 класс, 3 урок, Уравнения высших степенейСкачать

✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Быстрый способ решения квадратного уравненияСкачать