Доказать что прямые пересекаются и составить уравнение плоскости содержащей их

В этой статье собрана информация, необходимая для нахождения уравнения плоскости, проходящей через две заданные пересекающиеся или параллельные прямые. Сначала разобран принцип составления уравнения плоскости, которая проходит через две заданные прямые, после этого приведены подробные решения характерных примеров.

Навигация по странице.

Нахождение уравнения плоскости, проходящей через две пересекающиеся прямые.

Прежде чем приступать к нахождению уравнения плоскости, проходящей через две заданные пересекающиеся прямые, напомним одну теорему: в трехмерном пространстве через две пересекающиеся прямые проходит единственная плоскость. Это утверждение является следствием из двух аксиом геометрии:

• через три различные и не лежащие на одной прямой точки проходит единственная плоскость;
• если две несовпадающие точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

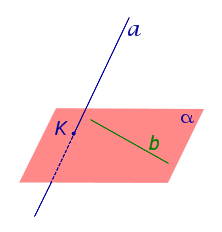
Таким образом, конкретную плоскость в трехмерном пространстве можно задать, указав две пересекающиеся прямые, лежащие в этой плоскости.

Теперь покажем, что плоскость, проходящая через две заданные пересекающиеся прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных прямых, а третья – на другой прямой.

Пусть заданные прямые a и b пересекаются в точке М . Отметим на прямой a две различные точки М₁ и М₂ (одна из них может совпадать с точкой M ), а на прямой b точку М₃ , отличную от точки М . Покажем, что плоскость М₁М₂М₃ есть плоскость, проходящая через заданные пересекающиеся прямые a и b .

Так как в плоскости М₁М₂М₃ лежат две точки прямой a (точки М₁ и М₂ ), то из озвученной в начале этого пункта аксиомы следует, что все точки прямой a лежат в плоскости М₁М₂М₃ , в частности, точка М . Тогда в плоскости М₁М₂М₃ лежат все точки прямой b , так как две несовпадающие точки прямой b (точки М и М₃ ) лежат в указанной плоскости. Следовательно, плоскость, проходящая через пересекающиеся прямые a и b , и плоскость, проходящая через три точки М₁ , М₂ и М₂ , совпадают.

Итак, поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , заданы две пересекающиеся прямые a и b , и требуется написать уравнение плоскости, проходящей через пересекающиеся прямые a и b .

Сведем решение этой задачи к нахождению уравнения плоскости, проходящей через три точки. Для этого нужно определить координаты двух различных точек M₁ и M₂ , лежащих на одной из заданных пересекающихся прямых, и координаты точки M₃ , лежащей на другой прямой и не являющейся точкой пересечения заданных прямых. Для нахождения координат точек М₁ , М₂ и М₃ все средства хороши. Например, можно получить параметрические уравнения прямой a в пространстве вида . Из них видны координаты точки М₁ (они получаются при ), а координаты точки М₂ можно вычислить, придав параметру любое ненулевое действительное значение (к примеру, ). После этого можно получить параметрические уравнения прямой b и при некотором значении параметра вычислить координаты точки М₃ , не забыв удостовериться, что она не является точкой пересечения заданных прямых (что она не лежит на прямой a ).

Будем считать, что координаты точек М₁ , М₂ и М₃ найдены. После этого мы можем написать уравнение плоскости, проходящей через три точки и в виде . Вычислив определитель матицы вида , мы получим общее уравнение плоскости М₁М₂М₃ , которое и будет уравнением плоскости, проходящей через две пересекающиеся прямые a и b .

Нахождение уравнения плоскости, проходящей через две параллельные прямые.

Прежде чем получить уравнение плоскости, проходящей через две заданные параллельные прямые, вспомним теорему: через две параллельные прямые проходит единственная плоскость. Эта теорема доказывается на основе аксиомы о единственной плоскости, проходящей через три заданные точки, с использованием утверждения: если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Таким образом, мы можем задать конкретную плоскость в трехмерном пространстве, указав две параллельные прямые, лежащие в этой плоскости.

Очевидно, что плоскость, проходящая через две заданные параллельные прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных параллельных прямых, а третья лежит на другой прямой.

Теперь можно приступать к нахождению уравнения плоскости, проходящей через две заданные параллельные прямые.

Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , заданы две параллельные прямые a и b и требуется составить уравнение плоскости, которая проходит через параллельные прямые a и b .

Эта задача, также как и задача о нахождении уравнения плоскости, проходящей через две заданные пересекающиеся прямые, сводится к составлению уравнения плоскости, проходящей через три точки. Действительно, мы можем определить координаты двух точек М₁ и М₂ , лежащих на одной из заданных параллельных прямых, и координаты точки М₃ , лежащей на другой прямой. После этого нам лишь нужно написать уравнение плоскости, проходящей через три точки и , в виде . Это уравнение является искомым уравнением плоскости, проходящей через две заданные параллельные прямые.

Примеры составления уравнения плоскости, проходящей через две прямые.

Итак, чтобы написать уравнение плоскости, проходящей через две заданные параллельные или пересекающиеся прямые, нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки. Покажем применение этого алгоритма при решении примеров.

Известно, что прямая a в прямоугольной системе координат Oxyz в трехмерном пространстве проходит через точку и пересекает координатную прямую Oy в точке . Напишите уравнение плоскости, проходящей через пересекающиеся прямые a и Oy .

Из условия нам известны координаты двух точек М₁ и М₂ , лежащих на прямой a . Очевидно, что точка лежит на координатной прямой Oy и не совпадает с точками М₁ и М₂ . Тогда плоскость, проходящая через три точки , и , есть плоскость, проходящая через пересекающиеся прямые a и Oy . Напишем ее уравнение:

.

Рассмотрим еще один пример, в котором координаты точек, лежащих на заданных пересекающихся прямых, не так очевидны.

Составьте уравнение плоскости, которая проходит через две пересекающиеся прямые a и b , заданные уравнениями и соответственно.

Сначала найдем координаты двух точек, лежащих на прямой a , и координаты точки, лежащей на прямой b .

Прямая, которую в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида , проходит через точку . Перейдем к параметрическим уравнениям этой прямой, чтобы определить координаты еще одной точки (обозначим ее М₂ ), лежащей на ней. Имеем , примем и из параметрических уравнений прямой вычислим координаты точки М₂ : . Следовательно, .

Очевидно, что прямая проходит через точку . Проверим, не является ли точка точкой пересечения заданных прямых, подставив ее координаты в уравнения прямой a : . Канонические уравнения прямой a обратились в тождества, следовательно, точка М₃ лежит на прямой a и является точкой пересечения заданных прямых. Таким образом, нам нужно взять другую точку М₃ , лежащую на прямой b , так как сейчас найденные точки М₁ , М₂ и М₃ лежат на одной прямой. Для этого мы также переходим к параметрическим уравнениям прямой b : , и вычисляем координаты точки М₃ , приняв : .

Теперь мы можем получить уравнение плоскости, проходящей через три точки , и , которое является искомым уравнением плоскости, проходящей через две заданные пересекающиеся прямые:

.

Не правда ли, что нахождение координат точек, лежащих на заданных прямых, является самым трудоемким процессом при составлении уравнения плоскости, проходящей через две пересекающиеся прямые?

Осталось рассмотреть пример составления уравнения плоскости, проходящей через две заданные параллельные прямые.

Напишите уравнение плоскости, проходящей через две параллельные прямые и .

По параметрическим уравнениям прямой при и вычислим координаты двух точек М₁ и М₂ :

Очевидно, что прямая проходит через точку .

Найдем уравнение плоскости, проходящей через три точки М₁ , М₂ и М₃ :

Это уравнение и есть искомое уравнение плоскости, проходящей через две заданные параллельные прямые.

.

2.3. Типовые задачи

В разделе 1 было получено уравнение плоскости проходящей через точку М0(x0,y0,z0) и с вектором нормали , где A2+B2+C2>0:

A(x – x0) + B(y – y0) + C(z – z0)=0. (*)

Рассмотрим теперь другие способы задания плоскости в пространстве.

Задача 1. Написать уравнение плоскости π, проходящей через три заданные точки М1(x1,y1,z1), М2(x2,y2,z2) и М3(x3,y3,z3) (рис. 5).

Решение: Чтобы написать уравнение искомой плоскости, достаточно знать координаты какой-либо точки на плоскости и координаты вектора нормали (уравнение (*). Точкой на плоскости может быть любая из заданных точек М1, М2 или М3, а вектором нормали может быть векторное произведение векторов [].

Поставленную задачу можно решить другим способом. Пусть М(x, y,z) — текущая точка на плоскости π. Тогда векторы =(x-x1,y-y1,z-z1), =(x2-x1,y2-y1,z2-z1) и =(x3-x1,y3-y1,z3-z1) лежат на плоскости π (компланарны). Условие компланарности этих векторов (равенство нулю их смешанного произведения) задает уравнение искомой плоскости π:

. (21)

Пример. Написать уравнение плоскости, проходящей через точки М1(1,1,1), М2(3,2,-1) и М3(4,1,0).

Для решения задачи воспользуемся вторым способом. Уравнение плоскости запишем в виде (21)

.

Разложив определитель по первой строке, получим

Или

– уравнение искомой плоскости с .

Заметим, что векторное произведение векторов =(2,1,–2) и =(3,0,–1) коллинеарно вектору нормали .

.

Задача 2. Написать уравнение плоскости π, проходящей через точку М0(x0,y0,z0) и прямую L (рис. 6): , если точка M0 не лежит на прямой L (иначе плоскость однозначно не определена). Точка М1(x1,y1,z1) принадлежит L, вектор – направляющий вектор.

Решение: Заданной точкой в уравнении (*) может быть любая из точек М1 или М0. Вектором нормали может служить векторное произведение векторов и :

=(A, B,C).

Задача 3. Написать уравнение плоскости, проходящей через две параллельные прямые.

и

Т. M1 (x1,y1,z1),

Т. M2 (x2,y2,z2) ,

Вектор – направляющий вектор прямых L1,L2 (рис. 7).

Вновь используем уравнение (*).

Точка на плоскости – любая из точек М1 или М2; вектором нормали =(A, B,C) может быть векторное произведение [,].

Задача 4. Доказать, что две прямые L1, L2 лежат в одной плоскости (пересекаются) и составить уравнение этой плоскости.

Решение задачи рассмотрим на примере.

Пусть и .

1. Проверим, лежат ли прямые L1 и L2 в одной плоскости. Для этого убедимся, что векторы , и компланарны.

Запишем параметрически заданную прямую L2 в каноническом виде

,

здесь М2(7,2,1) – точка на прямой L2, – ее направляющий вектор.

На прямой L1: М1(1,-2,5); . Вектор =(6,4,–4) (рис. 8).

Условием компланарности является равенство нулю смешанного произведения

,

Т. к. в полученном определителе две строки совпадают (при вычислении определителя общие множители первой строки и последнего столбца вынесены за знак определителя).

Итак, мы убедились, что прямые L1 и L2 пересекаются.

Точка плоскости π – любая из точек М1, М2 (возьмем, например, точку М1(1,–2,5)).

Вектор нормали =(А, B,C)= []== – 2+16+13.

Уравнение искомой плоскости π:

– 2(x – 1) + 16(y + 2) + 13(z – 5) = 0, или

2x – 16y – 13z + 31 = 0.

Задача 5. Определить взаимное расположение прямой L, заданной как пересечение двух непараллельных плоскостей:

L:

И плоскости π: A3x+B3y+C3z+D3=0.

Решение: Возможны следующие случаи:

А) прямая L и плоскость π не пересекаются (прямая параллельна плоскости и не имеет общих точек с плоскостью);

Б) прямая L пересекается с плоскостью в единственной точке;

В) прямая L лежит в плоскости – бесчисленное множество общих точек.

Эти задачи фактически были рассмотрены в разделе 2, когда прямая задавалась параметрическими или каноническими уравнениями.

Вообще говоря, нет надобности переходить от общего уравнения прямой к каноническому. Алгебраически задача сводится к исследованию и решению (если это возможно) системы уравнений

. (22)

Решение этой системы определяет координаты общих точек прямой и плоскости.

Воспользуемся методом Крамера. Обозначим определитель системы (22)

А определитель Δ1, Δ2, Δ3, полученные из Δ с помощью столбца свободных членов, соответственно:

.

Если определитель , то система (22) имеет единственное решение, и оно определяется по формулам Крамера:

,

Имеет место случай (б).

Если определитель , а хотя бы один из определителей Δ1, Δ2 или Δ3 отличен от нуля, система (22) не имеет решения (не совместна). Геометрически это означает, что прямая и плоскость не имеют общих точек (параллельны) – случай (а).

Если же все определители Δ =Δ1=Δ2=Δ3=0, то система (22) имеет бесчисленное множество решений. Прямая L целиком лежит на плоскости π (случай в)).

Задача 6. Определить точку Q, симметричную точке M0(x0,y0,z0), относительно плоскости

Решение. Запишем алгоритм решения задачи.

1. Составим уравнение прямой L, проходящей через точку M0(x0,y0,z0) и перпендикулярной плоскости π. Направляющим вектором этой прямой послужит вектор нормали

.

2. Найдём точку пересечения M1(x1,y1,z1) прямой L и плоскости π (см. раздел 2).

3. Точка M1 является серединой отрезка M0Q, и координаты точек M0, M1 и Q связаны формулами: x1=,y1=,z1=, откуда найдем координаты точки Q(x0,y0,z0)
(рис. 9):

XQ=2×1 – x0, yQ=2y1 – y0, zQ=2z1 – z0.

Аналогично решается и следующая задача.

Задача 7. Найти точку Q, симметричную точке M0(x0,y0,z0) относительно прямой

.

1. Составим уравнение плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно прямой L. Вектором нормали к этой плоскости (A, B,C) возьмем направляющий вектор =(l, m,n) прямой L.

π: l(x – x0) + m(y – y0) + n(z – z0)=0.

2. Найдем точку пересечения M1(x1,y1,z1) прямой L и плоскости π (см. раздел 2).

3. Точка M1 – середина отрезка M0Q, координаты точки Q определяются так же, как и в задаче 6.

Как доказать что прямые пересекаются в плоскости

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.

Тема урока

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых.

Определение скрещивающихся прямых

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема 1 (признак скрещивающихся прямых) и ее доказательство

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

Возможные случаи расположения прямых

Три случая расположения прямых

1) Прямые a и b пересекаются в некоторой точке С: (Рис. 2.). Как мы знаем, через две пересекающиеся прямые проходит единственная плоскость.

2) Прямые a и b параллельны: a || b (Рис. 3.). Если прямые параллельны, то они лежат в одной плоскости и не пересекаются.

Заметим, что и в первом, и во втором случае прямые лежали в одной плоскости.

3) Прямые a и b скрещиваются (Рис. 4.). То есть прямые a и b не лежат в одной плоскости.

Пример скрещивающихся прямых в треугольной пирамиде

Дана треугольная пирамида ABCD, АВС – плоскость основания, точка D не лежит в плоскости АВС (Рис. 5.). Почему прямые АВ и DC скрещивающиеся?

Прямая DC пересекает плоскость АВС в точке С, не лежащей на прямой АВ, а прямая АВ лежит в плоскости АВС. Значит, по признаку, прямые АВ и DC – скрещивающиеся. То есть противоположные ребра треугольной пирамиды лежат на скрещивающихся прямых.

Теорема 2 и ее доказательство

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.

Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α. Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α, значит, что прямая DC параллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.

Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.

Задача 1

Точка D не лежит в плоскости треугольника АВС, точки M, N, P – середины отрезков DA, DB и DC соответственно, точка K лежит на отрезке BN (Рис. 7.). Выясните взаимное расположение прямых.

Прямая ND — это другое обозначение прямой ВD. Прямая ВD и прямая АВ лежат в плоскости АВD и пересекаются.

Прямые PK и ВС лежат в одной плоскости. Значит, они либо параллельные, либо пересекаются. Проведем среднюю линию NP (N, P – середины отрезков DB и DC соответственно). По свойству средней линии, прямая NP параллельна прямой ВС. Через точку Р можно провести только одну прямую, параллельную прямой ВС, и это прямая NP. Значит, любая другая прямая, проходящая через точку Р, не параллельна прямой ВС. Значит, PK и ВС пересекаются.

В треугольнике ABD точки M и N – середины сторон АD и ВD. Значит, МN – средняя линия. По свойству средней линии, МN параллельна АВ.

В треугольнике ADС точки M и Р – середины сторон АD и СD. Значит, МР – средняя линия. По свойству средней линии, МР параллельна АС.

Прямая КN и прямая ВD – это одна и та же прямая. Прямая АС лежит в плоскости АВС, прямая ВD пересекает плоскость АВС в точке, не лежащей на прямой АС. Значит, по признаку, прямые ВD и АС – скрещивающиеся. То есть, прямые КN и АС- скрещивающиеся.

Прямая МD и прямая АD – это одна и та же прямая. Прямая ВС лежит в плоскости АВС, прямая АD пересекает плоскость АВС в точке, не лежащей на прямой ВС. Значит, по признаку, прямые АD и ВС – скрещивающиеся. То есть, прямые МD и ВС – скрещивающиеся.

Задача 2

Докажите, что если АВ и СD скрещиваются, то АD и ВС тоже скрещиваются.

Предположим, что прямые АD и ВС не скрещивающиеся, то есть лежат в одной плоскости. Значит, все точки А, В, С, D лежат в этой плоскости, значит прямые АВ и СD тоже лежат в этой плоскости. Но прямые АВ и СD скрещивающиеся по условию. Получили противоречие. Значит, прямые АD и ВС – скрещивающиеся.

Итоги урока

Итак, мы познакомились со скрещивающимися прямыми: дали определение, доказали признак скрещивающихся прямых. Также мы доказали теорему о том, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теперь нам известны все случаи взаимного расположения прямых в пространстве: они могут пересекаться, быть параллельными, быть скрещивающимися.

Список рекомендованной литературы

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.

3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил.

Рекомендованные ссылки на ресурсы интернет

1. Центр образования «Технологии обучения» (Источник).

2. Начертательная геометрия (Источник).

3. Виртуальная геометрия (Источник).

Рекомендованное домашнее задание

1. Какие прямые называются скрещивающимися?

2. Назовите возможные случаи взаимного расположения двух прямых в пространстве.

3. Дан параллелепипед (см. Рис. 8.). Каково взаимное расположение прямых:

4. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

Задания 1 (б, в), 3, 4 стр. 23.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

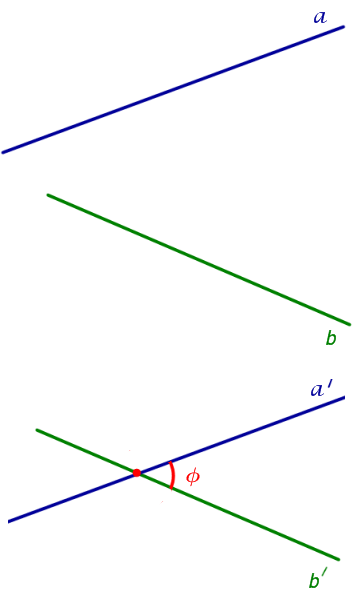
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		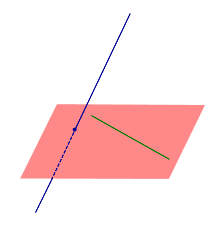Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		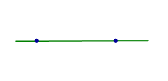Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		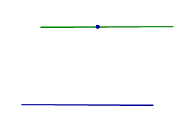Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		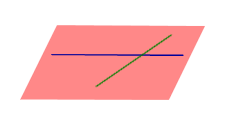Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

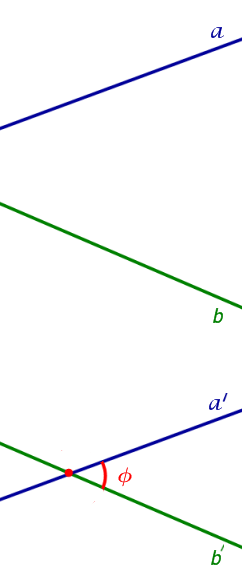
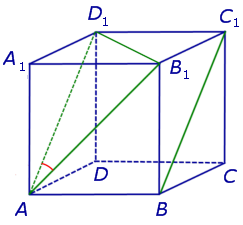
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

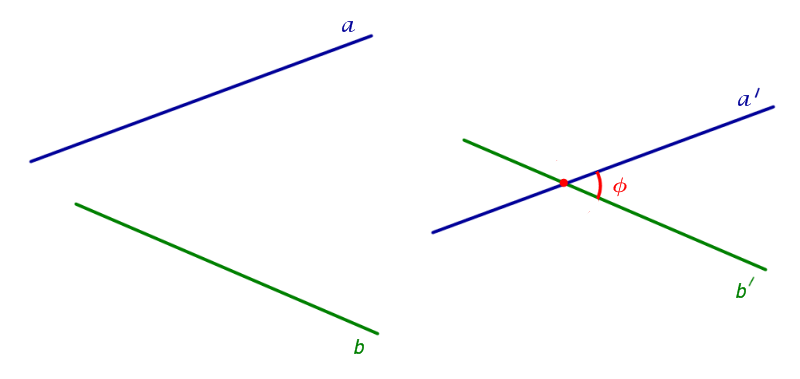
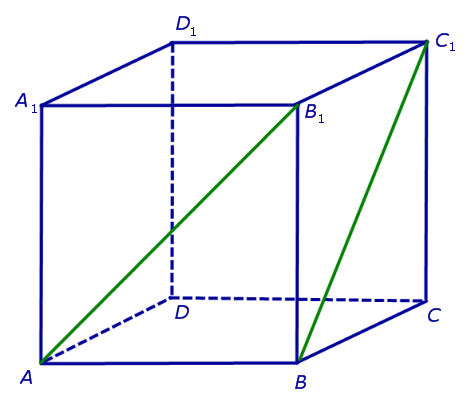
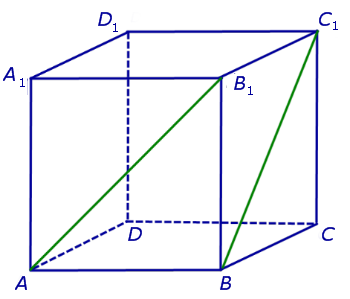
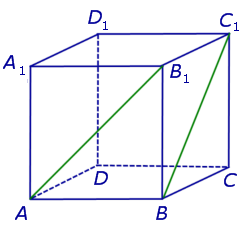
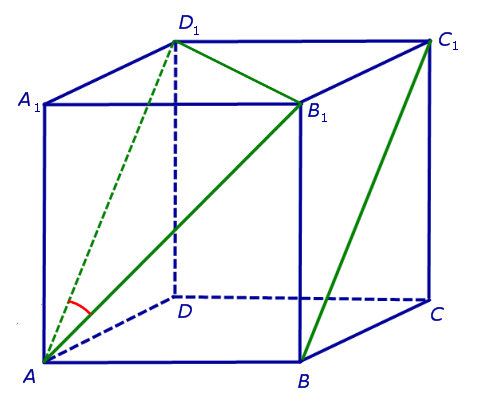
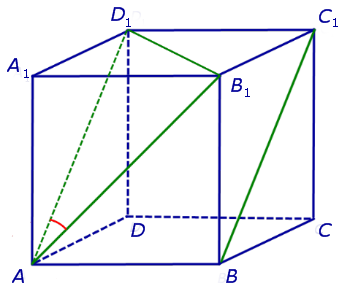
Угол между скрещивающимися прямыми

На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10 — 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .

Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) — нормальным вектором заданной плоскости альфа.

Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.

Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) — нормальным вектором плоскости α .

Определить, параллельны ли прямая x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , — 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( — 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .

Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ имеют значения a → = ( 2 , 3 , — 4 ) .

Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( — 4 ) · 5 = 0 .

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , — 1 , — 7 ) .

По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .

Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , — 4 , — 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , — 4 , — 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.

Запишем A B → , i → = 2 · 1 + ( — 4 ) · 0 + ( — 7 ) · 0 = 2 ≠ 0 .

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α — общим уравнением плоскости A x + B y + C z + D = 0 .

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .

Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.

Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x — 1 = y + 2 — 1 = z 3 параллельна плоскости 6 x — 5 y + 1 3 z — 2 3 = 0 .

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

x — 1 = y + 2 — 1 = z 3 ⇔ — 1 · x = — 1 · ( y + 2 ) 3 · x = — 1 · z 3 · ( y + 2 ) = — 1 · z ⇔ x — y — 2 = 0 3 x + z = 0

Чтобы доказать параллельность заданной прямой x — y — 2 = 0 3 x + z = 0 с плоскостью 6 x — 5 y + 1 3 z — 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x — y — 2 = 0 3 x + z = 0 6 x — 5 y + 1 3 z — 2 3 = 0 .

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1 — 1 0 2 3 0 1 0 6 — 5 1 3 2 3

1 — 1 0 2 0 3 1 — 6 0 1 1 3 — 11 1 3

1 — 1 0 2 0 3 1 — 6 0 0 0 — 9 1 3 .

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x — 1 = y + 2 — 1 = z 3 и плоскость 6 x — 5 y + 1 3 z — 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

Уравнение плоскости, проходящей через точку и прямую онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:

.

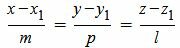(1)

Задача заключается в построении уравнения плоскости α, проходящей через точку M₀ и и через прямую L(Рис.1).

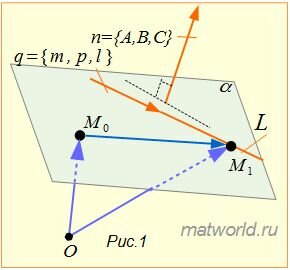Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(2)

Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁). Тогда уравнение плоскости, проходящей через точку M₁(x₁, y₁, z₁) имеет вид:

A(x−x1)+B(y−y1)+C(z−z1)=0.

(3)

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

Вычитая уравнение (3) из уравнения (2), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(5)

Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M₀ и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:

.

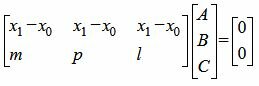(6)

Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.

Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.

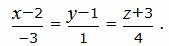(7)

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀)=M₀(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).

Вычитая уравнение (3) из уравнения (2), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(8)

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

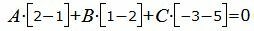(10)

(11)

Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

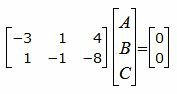(12)

Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:

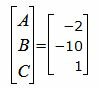Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:

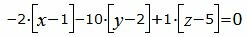(13)

Упростим уравнение (13):

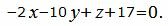(14)

Ответ: Уравнение плоскости, проходящей через точку M₀(1, 2, 5) и через прямую (7) имеет вид (14).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и через прямую L, заданной параметрическим уравнением:

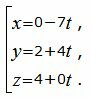(15)

Решение. Приведем параметрическое уравнение (15) к каноническому виду:

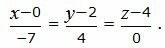(16)

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(17)

Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M₁(x₁, y₁, z₁) имеет вид:

A(x−x1)+B(y−y1)+C(z−z1)=0.

(18)

Вычитая уравнение (18) из уравнения (17), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(19)

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :

Am+Bp+Cl=0.

(20)

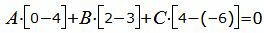(21)

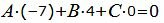(22)

Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

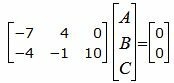(23)

Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:

Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:

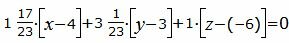(24)

Упростим уравнение (24):

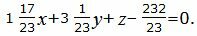(25)

Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.

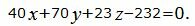(26)

Ответ: Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и через прямую (16) имеет вид (26).