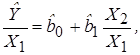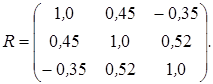Добавление в уравнение множественной регрессии новой объясняющей переменной коэффициента

Видео:Множественная регрессия в ExcelСкачать

Добавление в уравнение множественной регрессии новой объясняющей переменной коэффициента детерминации

Вид множественной линейной модели регрессионного анализа: Y = b₀ + b₁x_i1 + . + b_jx_ij + . + b_kx_ik + e_i где e_i — случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.

Назначение множественной регрессии : анализ связи между несколькими независимыми переменными и зависимой переменной.

Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии b_j показывает, на какую величину в среднем изменится результативный признак Y, если переменную X_j увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного анализа: Y = Xb + e где Y — случайный вектор — столбец размерности (n x 1) наблюдаемых значений результативного признака (y₁, y₂. y_n);
X — матрица размерности [n x (k+1)] наблюдаемых значений аргументов;
b — вектор — столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;
e — случайный вектор — столбец размерности (n x 1) ошибок наблюдений (остатков).

На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.

Задачи регрессионного анализа
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии b₀, b₁. b_k. Задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных X_i и Y:

• получить наилучшие оценки неизвестных параметров b₀, b₁. b_k;
• проверить статистические гипотезы о параметрах модели;
• проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Построение моделей множественной регрессии состоит из следующих этапов:

1. выбор формы связи (уравнения регрессии);
2. определение параметров выбранного уравнения;
3. анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения.

Множественная регрессия:

• Множественная регрессия с одной переменной
• Множественная регрессия с двумя переменными
• Множественная регрессия с тремя переменными

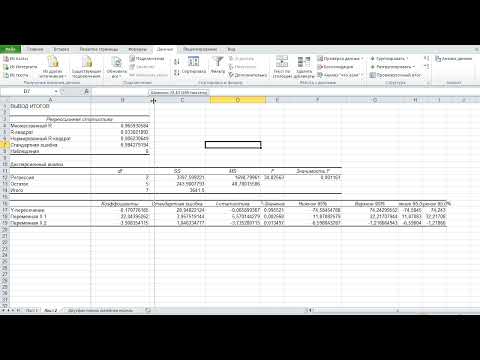
Видео:Множественная регрессияСкачать

Пример решения нахождения модели множественной регрессии

Модель множественной регрессии вида Y = b 0 +b 1 X 1 + b 2 X 2 ;
1) Найтинеизвестные b 0 , b 1 ,b 2 можно, решим систему трехлинейных уравнений с тремя неизвестными b 0 ,b 1 ,b 2 :

Для решения системы можете воспользоваться решение системы методом Крамера
2) Или использовав формулы

Для этого строим таблицу вида:

Выборочные дисперсии эмпирических коэффициентов множественной регрессии можно определить следующим образом:

Здесь z’ jj — j-тый диагональный элемент матрицы Z -1 =(X T X) -1 .

Приэтом:

где m — количество объясняющихпеременных модели.
В частности, для уравнения множественной регрессии Y = b 0 + b 1 X 1 + b 2 X 2 с двумя объясняющими переменными используются следующие формулы:


Или

или
,,.
Здесьr 12 — выборочный коэффициент корреляции между объясняющимипеременными X 1 и X 2 ; Sb j — стандартная ошибкакоэффициента регрессии; S — стандартная ошибка множественной регрессии (несмещенная оценка).
По аналогии с парной регрессией после определения точечных оценокb j коэффициентов β j (j=1,2,…,m) теоретического уравнения множественной регрессии могут быть рассчитаны интервальные оценки указанных коэффициентов.

Доверительный интервал, накрывающий с надежностью (1- α ) неизвестное значение параметра β j, определяется как

Видео:Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Проверка общего качества уравнения

Множественной регрессии

Для проверки общего качества уравнения регрессии обычно используется коэффициент детерминации R 2 , который характеризует долю дисперсии зависимой переменной Y, объясняемую регрессионной моделью, и определяется по формуле:

(3.27)

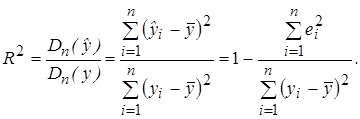
Свойства коэффициента R 2 подробно рассмотрены в разделе 2.4.

Для множественной регрессии коэффициент детерминации (или множественный коэффициент детерминации) является неубывающей функцией числа объясняющих переменных, т. е. добавление новой объясняющей переменной (фактора-аргумента Х) в модель никогда не уменьшает значение R 2 . Действительно, каждая новая объясняющая переменная может лишь дополнить информацию, объясняющую поведение зависимой переменной. В целом это уменьшает неопределенность в поведении исследуемой величины Y. Однако увеличение R 2 при добавлении новых переменных далеко не всегда приводит к улучшению качества регрессионной модели, так как эти переменные могут не оказывать существенного влияния на результативный признак. Поэтому, наряду с коэффициентом R 2 , для анализа используется скорректированный коэффициент детерминации 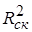, определяемый соотношением:

(3.28)

или с учетом (3.27)

. (3.29)

Можно заметить, что знаменатель в (3.29) является несмещенной оценкой общей дисперсии зависимой переменной Y, а числитель – несмещенной оценкой остаточной дисперсии (дисперсии случайных отклонений).

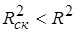
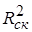
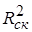
Скорректированный коэффициент детерминации устраняет (корректирует) неоправданный эффект, связанный с ростом R 2 при увеличении числа объясняющих переменных. Из (3.28) следует, что при m > 1 Можно показать, что увеличивается при добавлении новой объясняющей переменной только тогда, когда t-статистика для этой переменной по модулю больше единицы, т. е. когда ее коэффициент регрессии (параметр модели) считается относительно значимым. Таким образом, в определенной степени использование скорректированного коэффициента детерминации более предпочтительно для сравнения регрессионных моделей при изменении количества объясняющих переменных (регрессоров). Добавление в модель новых регрессоров может осуществляться до тех пор, пока растет .

В компьютерных пакетах приводятся данные как по R 2 , так и по 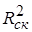, которые используются на практике для оценки суммарной меры общего качества построенной регрессионной модели.

В общем случае качество модели считается удовлетворительным, если R 2 > 0,5. Однако не следует рассматривать коэффициент детерминации как абсолютный показатель качества модели. Можно привести ряд примеров, когда неправильно специфицированные модели имели сравнительно высокие коэффициенты детерминации. Поэтому коэффициент детерминации в современной эконометрике следует рассматривать лишь как один из показателей, который необходим для анализа строящейся модели.

Анализ общей (совокупной) статистической значимости уравнения множественной регрессии осуществляется на основе проверки основной гипотезы об одновременном равенстве нулю всех коэффициентов при объясняющих переменных:

Если данная гипотеза не отклоняется, то естественно считать уравнение модели статистически незначимым, т. е. не выражающим существенную линейную связь между Y и Х₁, Х₂, …, Х_m.

Напомним (см. раздел 2.4.3), что общая дисперсия зависимой переменной D_n(y) может быть представлена в виде суммы двух составляющих:

где D_n(y) – соответственно, дисперсия, объясняемая уравнением множественной регрессии, и необъясняемая (остаточная) дисперсия, характеризующая влияние неучтенных факторов.

Исходя из этого проводится дисперсионный анализ для проверки гипотезы Н₀ (F-тест).

Строится проверочная F-статистика:

(3.30)

где – объясняемая дисперсия (в уравнении множественной регрессии вместе со свободным членом оценивается k = m + 1 параметров); – остаточная дисперсия. При выполнении предпосылок МНК построенная статистика имеет распределение Фишера с числами степеней свободы v₁ = m, v₂ = n — m — 1. Поэтому гипотеза Н₀ отклоняется, если при заданном уровне значимости a значение F_набл, рассчитанное по формуле (3.30), больше, чем критическое значение F_кр = F_{a; m; n — 1 — m} (F_набл > F_кр), и делается вывод о статистической значимости уравнения множественной регрессии. В противном случае (F_набл > F_кр) нет оснований для отклонения Н₀. Это означает, что объясняемая построенной моделью дисперсия соизмерима с дисперсией, вызванной неучтенными факторами, а следовательно, общее качество модели невысоко.

Если рассчитан коэффициент детерминации R 2 , то критерий значимости уравнения регрессии (3.30) может быть представлен в следующем виде:

(3.31)

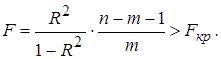
Критерий (3.31) обычно используется на практике для тестирования гипотезы о статистической значимости коэффициента детерминации (Н₀ : R 2 = 0; Н₁ : R 2 > 0) которая эквивалентна гипотезе об общей статистической значимости уравнения множественной регрессии.

Отметим, что в отличие от парной регрессии, где t-тест и F-тест равносильны, в случае множественной регрессии коэффициент R 2 приобретает самостоятельную значимость.

Пример 3.2. Оценим статистическую значимость построенной модели.

Пусть при оценке регрессии с тремя объясняющими переменными ( по 30 наблюдениям получено значение коэффициента детерминации R 2 = 0,7. Тогда, наблюдаемое значение F-ста­тистики . По таблице критических точек распределения Фишера найдем F_{0,05; 3; 26} = 2,98 при заданном уровне значимости a = 0,05. Поскольку F_набл = 20,2 > F_кр = 2,98, то нулевая гипотеза отклоняется, т. е. отвергается предположение о незначимости линейной связи.

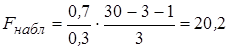
Мультиколлинеарность

Весьма нежелательным эффектом, который может проявляться при построении моделей множественной регрессии и искажать статистическую информацию, полученную по модели, является мультиколлинеарность [1,28,33]– линейная взаимосвязь двух или нескольких объясняющих переменных. Различают функциональную и корреляционную формы мультиколлинеарности.

При функциональной форме мультиколлинеарности по крайней мере два регрессора связаны между собой линейной функциональной зависимостью. В этом случае определитель матрицы Х Т Х равен нулю в силу присутствия линейно зависимых вектор-столбцов (нарушается предпосылка 5 МНК), что приводит к невозможности решения соответствующий системы уравнений и получения оценок параметров регрессионной модели.

Однако в эконометрических исследованиях мультиколлинеарность чаще всего проявляется в более сложной корреляционной форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Ниже рассмотрены некоторые способы обнаружения, а также уменьшения и устранения мультиколлинеарности.

Один из таких способов заключается в исследовании матрицы Х Т Х. Если ее определитель близок к нулю, то это может свидетельствовать о наличии мультиколлинеарности. В этом случае наблюдаются значительные стандартные ошибки коэффициентов регрессии и их статистическая незначимость по t-критерию, хотя в целом регрессионная модель может оказаться значимой по F-тесту.

Другой подход состоит в анализе матрицы парных коэффициентов корреляции между объясняющими переменными (факторами). Если бы факторы не коррелировали между собой, то корреляционная матрица R была бы единичной матрицей, поскольку все недиагональные элементы (х_i ¹ x_j) равны нулю. Определитель такой матрицы равен единице [Тимофеев, 2013]. Например, для модели, включающей три объясняющих переменных , в этом случае имеем:

. (3.32)

Если же, наоборот, между факторами-аргументами существует полная линейная зависимость и все коэффициенты корреляции равны 1 (|r_ij| = 1), то определитель матрицы межфакторной корреляции равен нулю

. (3.33)

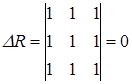
Таким образом, чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность объясняющих переменных и ненадежнее оценки множественной регрессии, полученные с использованием МНК.

Если в модели больше двух объясняющих переменных, то для обнаружения мультиколлинеарности полезно находить частные коэффициенты корреляции, поскольку парные коэффициенты корреляции определяют силу линейной зависимости между двумя факторами без учета влияния на них других объясняющих переменных. Например, между двумя экономическими переменными может наблюдаться высокий положительный коэффициент корреляции совсем не потому, что одна из них стимулирует изменение другой, а вследствие того, что обе эти переменные изменяются в одном направлении под влиянием других факторов, присутствующих в модели. Поэтому возникает необходимость оценки действительной тесноты (силы) линейной связи между двумя факторами, очищенной от влияния других переменных. Параметр, определяющий степень корреляции между двумя факторами Х_i и X_j при исключении влияния остальных переменных называется частным коэффициентом корреляции.

Например, в случае модели с тремя объясняющими переменными Х₁, Х₂, Х₃ частный коэффициент корреляции между Х₁ и Х₂ рассчитывается по формуле:

(3.34)

Частный коэффициент корреляции может существенно отличаться от «обычного» парного коэффициента корреляции r₁₂. Пусть, например, r₁₂ = 0,5; r₁₃ = 0,5; r₂₃ = -0,5. Тогда частный коэффициент корреляции r_12.3 = 1 (3.34), т. е. при относительно невысоком коэффициенте корреляции r₁₂ частный коэффициент корреляции указывает на высокую зависимость (коллинеарность) между переменными Х_i и X_j.

Таким образом, для обоснованного вывода о корреляции между объясняющими переменными множественной регрессии необходимо рассчитывать частные коэффициенты корреляции.

Частный коэффициент корреляции r_{ij.1, 2, …, m}, как и парный коэффициент r_ij, может принимать значения от -1 до 1. Присутствие в модели пар переменных, имеющих высокие коэффициенты частной корреляции (обычно больше 0,8), свидетельствует о наличии мультиколлинеарности.

Для устранения или уменьшения мультиколлинеарности используется ряд методов, простейшим из которых является исключение из модели одной или нескольких коррелированных переменных. Обычно решение об исключении какой-либо переменной принимается на основании экономических соображений. Следует заметить, что при удалении из анализа объясняющей переменной можно допустить ошибку спецификации. Например, при изучении спроса на некоторый товар в качестве объясняющих переменных целесообразно использовать цену данного товара и цены товаров-заменителей, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, вероятнее всего, допустим ошибку спецификации. Вследствие этого можно получить смещенные оценки и сделать ненадежные выводы.

Иногда для уменьшения мультиколлинеарности достаточно (если это возможно) увеличить объем выборки. Например, при использовании ежегодных показателей можно перейти к поквартальным данным. Увеличение количества данных сокращает дисперсии коэффициентов регрессионной модели и тем самым увеличивает их статистическую значимость.

В ряде случаев минимизировать либо вообще устранить мультиколлинеарность можно с помощью преобразования переменных, в результате которого осуществляется переход к новым переменным, представляющим собой линейные или относительные комбинации исходных [11].

Например, построенная регрессионная модель имеет вид:

(3.35)

причем Х₁ и Х₂ – коррелированные переменные. В этом случае целесообразно оценивать регрессионные уравнения относительных величин:

.

Следует ожидать, что в моделях, построенных аналогично (3.36), эффект мультиколлинеарности не будет проявляться.

Существуют также другие, более теоретически разработанные способы обнаружения и подавления мультиколлинеарности, подробное описание которых выходит за рамки данной книги. Одним из таких методов является факторный анализ. Сущностью факторного анализа является процедура вращения факторов, т.е. перераспределение дисперсии по определённому методу с целью получения максимально простой и наглядной структуры факторов (выделение главных компонент) [23,35]. В результате проведения факторного анализа можно соответствующим образом сократить число переменных, тем самым избежать проявления мультиколлинеарности. При этом в один фактор объединяются сильно коррелирующие между собой переменные, что позволяет проводить регрессионный анализ на главных компонентах.

Факторный анализ играет большую самостоятельную роль в экономике и, прежде всего, разработан для поиска ненаблюдаемых, латентных переменных (факторов), имеющих определённый социально-экономический смысл [23].

Следует заметить, что если основная задача, решаемая с помощью эконометрической модели – прогнозирование поведения реального экономического объекта, то при общем удовлетворительном качестве модели проявление мультиколлинеарности не является слишком серьезной проблемой, требующей приложения больших усилий по ее выявлению и устранению, т. к. в данном случае наличие мультиколлинеарности не будет существенно сказываться на прогнозных качествах модели. Таким образом, вопрос о том – следует ли серьезно заниматься проблемой мультиколлинеарности или «смириться» с ее проявлением – решается исходя из целей и задач эконометрического анализа.

Вопросы и упражнения для самопроверки

1. Какова общая структура модели множественной линейной регрессии?

2. Опишите алгоритм определения коэффициентов множественной линейной регрессии (параметров модели) по МНК в матричной форме.

3. Как определяется статистическая значимость коэффициентов регрессии?

4. В чем суть скорректированного коэффициента детерминации и его отличие от обычного R 2 ?

5. Как используется F-статистика во множественном регрессионном анализе?

6. Вычислите величину стандартной ошибки регрессионной модели со свободным членом и без него, если 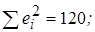n = 30; m = 3.

7. На основе n = 30 наблюдений оценена модель с тремя объясняющими переменными. Получены следующие результаты:

Стандартные ошибки (2,5) (1,6) (2,8) (0,07)

Проведите необходимые расчеты и занесите данные в скобки. Сделайте выводы о существенности коэффициентов регрессии на уровне значимости a =0,05.

8. Имеются данные о ставках месячных доходов по трем акциям за шестимесячный период:

Есть основания предполагать, что доходы по акции С(Y) зависят от доходов по акциям А(X₁) и В(X₂). Необходимо:

а) составить уравнение регрессии Y по X₁ и X₂ с использованием МНК (указание: для удобства вычислений сумм первых степеней, квадратов и попарных произведений переменных составьте вспомогательную таблицу);

б) найти множественный коэффициент детерминации R 2 и оценить общее качество построенной модели;

в) проверить значимость полученного уравнения регрессионной модели на уровне a = 0,05.

9. Объясните суть матрицы ковариаций случайных отклонений.

10. Дайте определение и объясните смысл мультиколлинеарности факторов-аргументов.

11. Каковы основные последствия мультиколлинеарности?

12. Какие вы знаете способы обнаружения мультиколлинеарности?

13. Как оценивается степень коррелированности между двумя объясняющими переменными?

14. Перечислите основные методы устранения мультиколлинеарности.

15. В чем заключается сущность факторного анализа?

16. Как определяются парный и частный коэффициенты корреляции для независимых переменных.

17. Для модели с тремя независимыми переменными X₁, X₂, X₃ построенной по n = 50 наблюдениям, определена следующая корреляционная матрица:

б) определить, имеет ли место мультиколлинеарность для уравнения регрессии.

Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Множественная регрессия и корреляция

Решение Тестовых заданий

Парная регрессия и корреляция

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

в) экспериментальный (табличный).

Ответ: б) графический.

В парной регрессии выбор вида математической функции 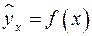может быть осуществлен тремя методами:

2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции.

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

Отчет: б) не менее 7 наблюдений

Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при должен рассчитываться хотя бы по 7 наблюдениям.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

Ответ: б) минимизации дисперсии результативного признака

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна:

.

4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

Ответ: а) показывает среднее изменение результата с изменением фактора на одну единицу

Параметр называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

в) ничего определенного сказать нельзя.

Ответ: а) да (пример рассматривали на паре с доходами и расходами)

6. Суть коэффициента детерминации состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

Ответ: б) характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:

, (1.22)

т.е. имеет тот же смысл, что и в линейной регрессии; .

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;

б) -критерий Фишера;

в) средняя ошибка аппроксимации .

Ответ: а) коэффициент детерминации

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:

, (1.7)

где , .

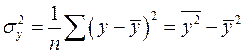
8. Значимость уравнения регрессии в целом оценивает:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .

Ответ: а) F-критерий Фишера

Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа.

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

Ответ: в) шаговом регрессионном анализе

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

1. Метод исключения – отсев факторов из полного его набора.

2. Метод включения – дополнительное введение фактора.

3. Шаговый регрессионный анализ – исключение ранее введенного фактора.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а -критерий меньше табличного значения.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

Ответ: в) никогда

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной от среднего значения раскладывается на две части – «объясненную» и «необъясненную»:

,

где – общая сумма квадратов отклонений; – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.

11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

Ответ: б)

Фактическое значение -критерия Фишера (1.9) сравнивается с табличным значением при уровне значимости и степенях свободы и . При этом, если фактическое значение -критерия больше табличного, то признается статистическая значимость уравнения в целом.

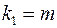
Для парной линейной регрессии , поэтому

.

12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

Ответ: в) .

Величина стандартной ошибки совместно с -распределением Стьюдента при степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.

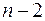
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение -критерия Стьюдента: которое затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы

13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

Ответ: а)

Общая

14. Для оценки значимости коэффициентов регрессии рассчитывают:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .

Ответ: в) коэффициент детерминации .

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина меньше . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:

,

где , .

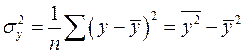
Соответственно величина характеризует долю дисперсии , вызванную влиянием остальных, не учтенных в модели, факторов.

15. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;

б) :

в) .

Ответ: в) .

К внутренне нелинейным моделям можно отнести следующие модели: ,

16. Какое из уравнений является степенным:

а) ;

б) :

в) .

Ответ: б) :

Существуют регрессии, нелинейные по оцениваемым параметрам, например

– степенная – .

17. Параметр в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

Ответ: б) коэффициентом эластичности;

Широкое использование степенной функции связано с тем, что параметр в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид:

.

Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора , то обычно рассчитывается средний коэффициент эластичности:

.

18. Коэффициент корреляции может принимать значения:

Ответ: а) от –1 до 1

Линейный коэффициент корреляции находится в пределах: . Чем ближе абсолютное значение к единице, тем сильнее линейная связь между факторами (при имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.

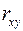
19. Для функции средний коэффициент эластичности имеет вид:

а) ;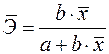

б) ;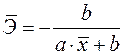

в) .

Ответ: б)

Вид функции,	Первая производная,	Средний коэффициент эластичности,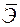

20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;

б) ;

в) .

Ответ: в) .

Среди нелинейных моделей наиболее часто используется степенная функция , которая приводится к линейному виду логарифмированием:

;

;

,

где . Т.е. МНК мы применяем для преобразованных данных:

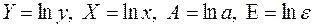
а затем потенцированием находим искомое уравнение.

Множественная регрессия и корреляция

1. Добавление в уравнение множественной регрессии новой объясняющей переменной:

а) уменьшает значение коэффициента детерминации;

б) увеличивает значение коэффициента детерминации;

в) не оказывает никакого влияние на коэффициент детерминации.

Ответ: б) увеличивает значение коэффициента детерминации

При дополнительном включении в регрессию фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться.

2. Скорректированный коэффициент детерминации:

а) меньше обычного коэффициента детерминации;

б) больше обычного коэффициента детерминации;

в) меньше или равен обычному коэффициенту детерминации;

Ответ: в) меньше или равен обычному коэффициенту детерминации

Скорректированный коэффициент множественной детерминации определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов.

В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений . Если число параметров при равно и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов делится на число степеней свободы остаточной вариации , а общая сумма квадратов отклонений на число степеней свободы в целом по совокупности .

Формула скорректированного индекса множественной детерминации имеет вид:

3. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:

в) не изменяется.

Ответ: б) уменьшается

Поскольку , то величину скорректированного индекса детерминации можно представить в виде:

.

Чем больше величина , тем сильнее различия и .

4. Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:

а) ;

б) ;

в) .

Ответ: в)

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Остаточная

5. Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:

а) ;

б) ;

в) .

Ответ: а)

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая

6. Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:

а) ;

б) ;

в) .

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Факторная

7. Множественный коэффициент корреляции . Определите, какой процент дисперсии зависимой переменной объясняется влиянием факторов и :

Процентное выражение дисперсии зависимой переменной y вычисляется:

; 0,9*100=90%

8. Для построения модели линейной множественной регрессии вида необходимое количество наблюдений должно быть не менее:

В линейной множественной регрессии параметры при называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

9. Стандартизованные коэффициенты регрессии :

а) позволяют ранжировать факторы по силе их влияния на результат;

б) оценивают статистическую значимость факторов;

в) являются коэффициентами эластичности.

Ответ: а) позволяют ранжировать факторы по силе их влияния на результат

Ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( -коэффициенты).

10. Частные коэффициенты корреляции:

а) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;

б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;

в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.

Ответ: в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

11. Частный -критерий:

а) оценивает значимость уравнения регрессии в целом;

б) служит мерой для оценки включения фактора в модель;

в) ранжирует факторы по силе их влияния на результат.

Ответ: б) служит мерой для оценки включения фактора в модель

Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

12. Несмещенность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: б) что математическое ожидание остатков равно нулю

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

13. Эффективность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: а) что она характеризуется наименьшей дисперсией

Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

14. Состоятельность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: в) увеличение ее точности с увеличением объема выборки

Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки

15. Укажите истинное утверждение:

а) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;

б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;

в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.

Ответ: в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.

16. При наличии гетероскедастичности следует применять:

б) обобщенный МНК;

в) метод максимального правдоподобия.

Ответ: а) обычный МНК

При использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии представляет собой взвешенную величину по отношению к обычному МНК с весом .

17. Фиктивные переменные – это:

а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

б) экономические переменные, принимающие количественные значения в некотором интервале;

в) значения зависимой переменной за предшествующий период времени.

Ответ: а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.

18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:

Предполагая при параметре 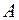независимую переменную, равную 1, имеем следующую матрицу исходных данных:

В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям

,

т.е. каждое уравнение включает только одну фиктивную переменную или .

🌟 Видео

Коэффициент детерминации. Основы эконометрикиСкачать

Построение модели множественной регрессии в программе GretlСкачать

Множественная регрессия в программе Statistica (Multiple regression)Скачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать

Парная регрессия: линейная зависимостьСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать

Лекция 8. Множественная линейная регрессияСкачать

Математика #1 | Корреляция и регрессияСкачать

EViews. Урок 1. Построение модели множественной регрессии.Скачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Множественная регрессия в MS Excel. Быстрое решение. И подробное решение. Калькулятор!Скачать