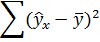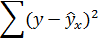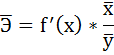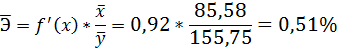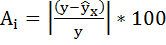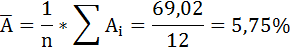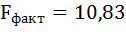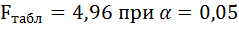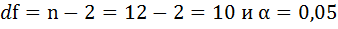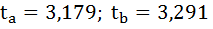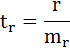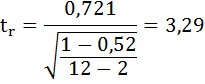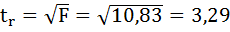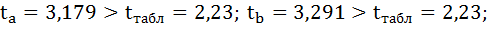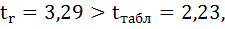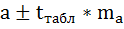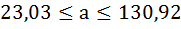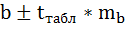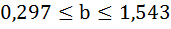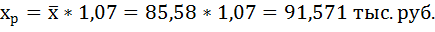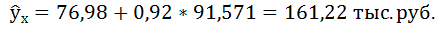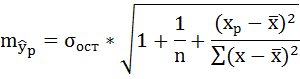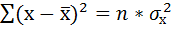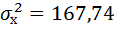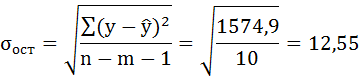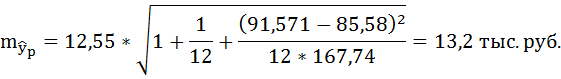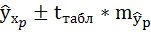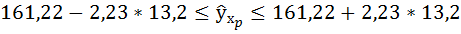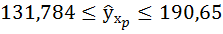Xf = 7, >’i = 4. Вычислите коэффициенты h0, линейной регрессии. Сравните их с коэффициентами b0, h примера 2.3.1.
Для уравнения регрессии у = 200-78л выберите отклонение выборочного (фактического) значения от расчетного для точки с координатами (2;50)
Задание № 2 Вычислите доверительный интервал с вероятностью 95 % для коэффициента регрессии для модели у = 3-2-х + е, построенной на основании 20 наблюдений, если известны у* статистики для параметров регрессии
Выберите один из следующих ответов:
Проставьте номера значений R 2 напротив соответствующей характеристики.
- ? на случайные факторы приходится 20 % дисперсии зависимой переменной
- ? на случайные факторы приходится 0,2 % дисперсии зависимой переменной
- ? на зависимую переменную не оказывают влияния случайные факторы
- ? доля дисперсии зависимой переменной, объясненная уравнением, составляет 0,7
При проверке оценке значимости оцениваемого параметра регрессионной модели выдвигаются статистические гипотезы. Нулевая гипотеза /7(): значение оцениваемого параметра равно нулю; альтернативная гипотеза : значение оцениваемого параметра отлично от нуля. При этом возможны отдельные случаи, когда.
Укажите не менее двух вариантов ответа
- 1. Параметр значим с вероятностью 90 %, но незначим с вероятностью 95 %
- 2. Параметр значим с вероятностью 99 %, но незначим с вероятностью 95 %
- 3. Параметр незначим с вероятностью 99 %, но значим с вероятностью 95 %
- 4. Параметр незначим с вероятностью 90 %, но значим с вероятностью 95 %
|
Уравнение регрессии вида
Укажите не менее двух вариантов ответа
- 1. Линейным по параметрам.
- 2. Нелинейным по переменным.
- 3. Линейным по переменным.
- 4. Нелинейным по параметрам.
|
|
Для регрессионной модели вида
Y = р() + Р] • X + ?, рассчитаны дисперсии:
Тогда величина коэффициента детерминации может быть рассчитана по формулам .
Видео:Математика #1 | Корреляция и регрессияСкачать
Рассчитайте множественный коэффициент корреляции, коэффициент детерминации и коэффициенты множественной регрессии.
Выберите меню Данные, Анализ данных, Регрессия.
Поместите курсор в окно Входной интервал Y и обведите мышью столбец с данными, результативного признака (Валовым региональным продуктом), включая и заголовок столбца.
Поместите курсор в окно Входной интервал X и обведите мышью все столбцы с данными факторных признаков, включая и заголовки столбцов.
Активизируйте опцию Метки в первой строке.
Опция Уровень надёжности по умолчанию настроена на 5% ошибку. Если потребуется другая точность вычисления, следует указать её.
На новом листе отображается таблица:
В таблице Регрессионная статистика сгенерированы результаты по регрессионной статистике. Эти результаты соответствуют следующим статистическим показателям:
Множественный R – коэффициенту корреляции R;
R-квадрат — коэффициенту детерминации R 2 ;
Стандартная ошибка — остаточному стандартному отклонению
Наблюдения — числу наблюдений п.
В таблице Дисперсионный анализ сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R-квадрат.
Столбцы имеют следующую интерпретацию:
Столбец df — число степеней свободы.
Для строки Регрессия число степеней свободы определяется количеством факторных признаков m в уравнении регрессии kф=m=5.
Для строки Остаток число степеней свободы определяется числом наблюдений n и количеством переменных в уравнении регресси: kо = п – (m+1)=79 – 6=73.
Столбец SS — сумма квадратов отклонений.
Для строки Регрессия — это сумма квадратов отклонений теоретических данных от среднего:
Для строки Остаток – это сумма квадратов отклонений эмпирических данных от теоретических:
Для строки Итого — это сумма квадратов отклонений эмпирических данных от среднего: или
Столбец MS – дисперсии, рассчитываемые по формуле:
Для строки Регрессия – это факторная дисперсия.
Для строки Остаток – это остаточная дисперсия .
Столбец F – расчетное значение F-критерия Фишера вычисляемое по формуле
Столбец Значимость F– значение уровня значимости соответствующее вычисленному значению Fp. Определяется с помощью функции
Поскольку Значимость F = 1,23462E-25 меньше F= 65,7003778, уравнение регрессии значимо.
В следующей таблице сгенерированы значения коэффициентов регрессии аi,- и их статистические оценки.
Столбцы имеют следующую интерпретацию:
Стандартная ошибка — стандартные ошибки коэффициентов ai
t-статистика — расчетные значения t-критерия, вычисляемые по формуле
5. Р-значение – значения уровней значимости, соответствующие вычисленным значениям tp. Определяются с помощью функции
6. Нижние 95 % и Верхние 95 % — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии. Для нахождения границ доверительных интервалов с помощью функции = СТЬДРАСПОБР (tp; n – т – 1) рассчитывается критическое значение t-критерия tкp, а затем по формулам
Нижние 95% = Коэффициент – Стандартная ошибка*tкр;
Верхние 95% = Коэффициент + Стандартная ошибка*tкр.
вычисляются соответственно нижние и верхние границы доверительных интервалов.
Анализ сгенерированных таблиц.
Рассчитанные ячейки коэффициенты регрессии аi,- позволяют построить уравнение, выражающее зависимость Валового регионального продукта на душу населения Y от величины Итогов миграции населения X1 , Количества правонарушений Х2, Средней начисленной заработной платы, руб. Х3, Денежных доходов на душу населения, млн.руб. Х4, Объема промышленного производства, млн. руб. Х5:
Значение множественного коэффициента детерминации R 2 = 0,818182674 показывает, что 81,82 % общей вариации результативного признака объясняется вариацией факторных признаков Х1, Х2, Х3, Х4, Х5, а на 18,18 % другими неучтёнными факторами. Значит, выбранные факторы существенно влияют на прибыль предприятий, что подтверждает правильность их включения в построенную модель.
Рассчитанный уровень значимости = 1,23462E-25 2 .
Сравнивая попарно элементы массивов Коэффициенты и Стандартная ошибка, видим, что коэффициент регрессии а1= -0,513940943 по абсолютной величине меньше, чем его стандартная ошибка = 0,625850921. Таким образом, фактор X1 следует исключить из уравнения регрессии.
Стандартные ошибки остальных коэффициентов аi меньше своих стандартных ошибок. Но не все они являются значимыми, о чем можно судить по значениям показателя Р-значение, которые должны быть меньше заданного уровня значимости α = 0,05. Таким незначимым является свободный член уравнения регрессии (коэффициент в строке Y-пересечение), его значимость 0,24906735 больше 0,05 и фактор X2 (Выявлено правонарушений) 0,1036179.
Подводя итог предварительному анализу уравнения регрессии, можно сделать вывод, что его целесообразно пересчитать без фактора X1, и X2, и свободного члена, которые не является статистически значимыми. В диалоговом окне Регрессия необходимо задать новые параметры, и следует активизировать флажок Константа-ноль (для исключения свободного члена).
Пересчитывая значения уравнения регрессии без свободного члена, а также фактора Х1 и Х2
получаем следующую таблицу:
Сравнивая попарно элементы массивов Коэффициенты и Стандартная ошибка, видим, что абсолютные значения факторов аi больше, чем их стандартные ошибки. К тому же эти коэффициенты являются значимыми, о чем можно судить по значениям показателя Р-значение, которые меньше заданного уровня значимости α = 0,05. Значения #Н/Д в строке Y-пересечение, означает отсутствие свободного члена в уравнении регрессии.
Таким образом, получаем новое уравнение регрессии:
Экономическая сущность коэффициентов аi в полученном уравнении регрессии состоит в том, что они показывают степень влияния каждого фактора на результативный признак (Внутренний региональный продукт на душу населения). Так, увеличение Средней начисленной заработной платы на 1 рубль ведет к ведёт в увеличению Внутреннего регионального продукта на душу населения на 7,31 руб., увеличение Денежных доходов населения на 1 млн. руб. ведет к росту Внутреннего регионального продукта на душу населения на 7,28 руб., увеличение Объёма промышленного производства на 1 млн. рублей ведет к росту Внутреннего регионального продукта на душу населения на 4,19 руб.
Видео:МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
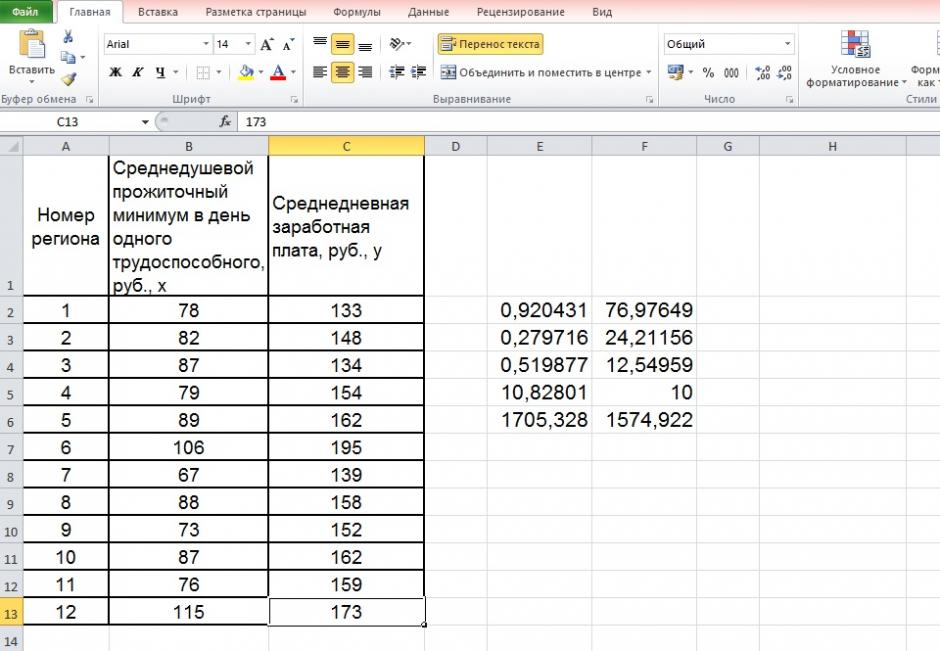
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
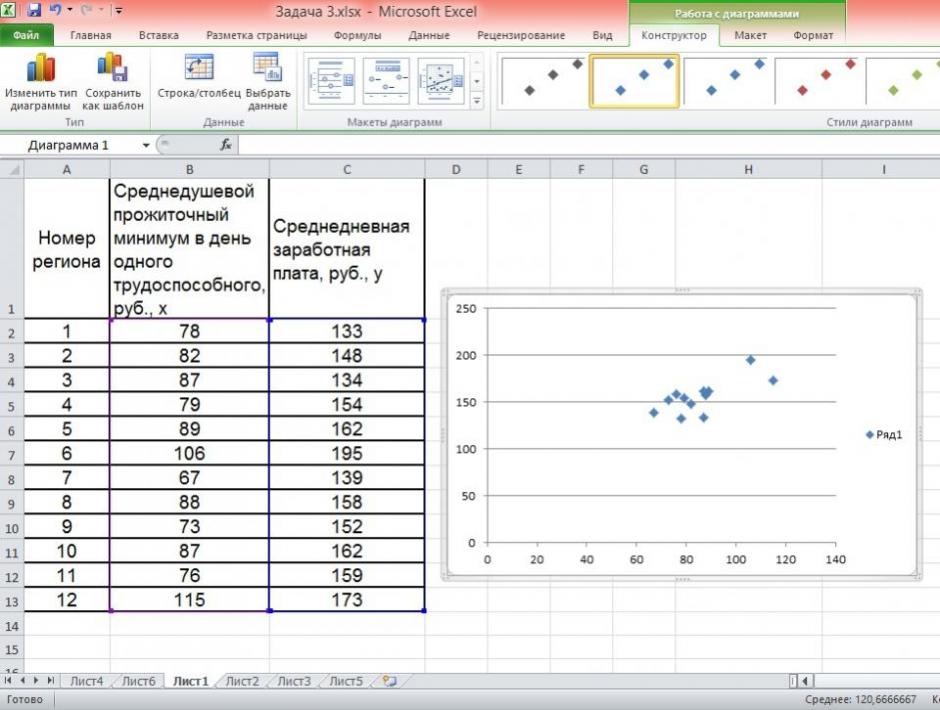
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
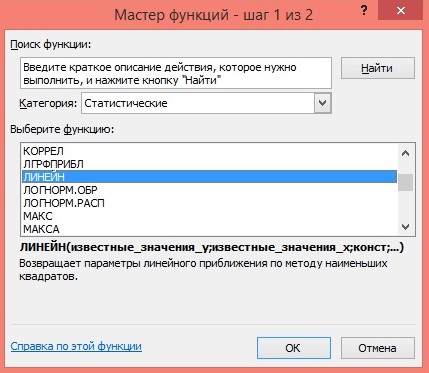
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
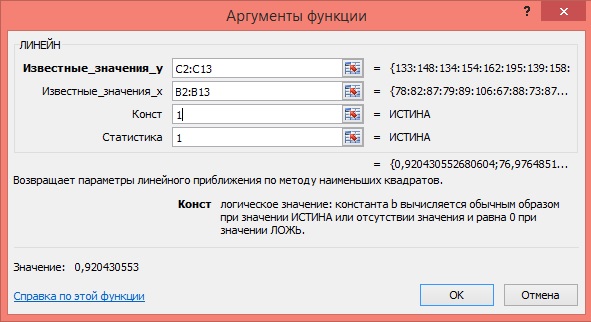
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
.
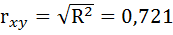
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
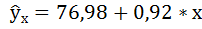
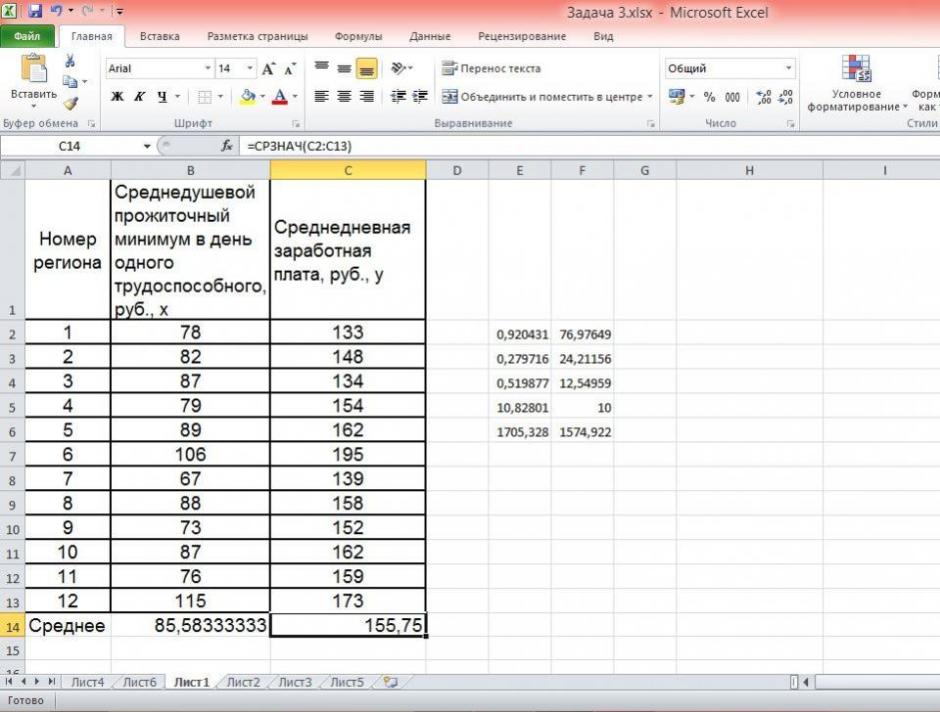
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
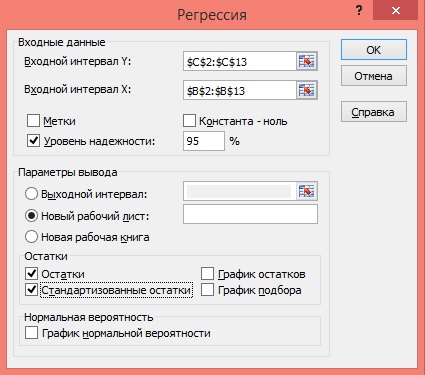
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
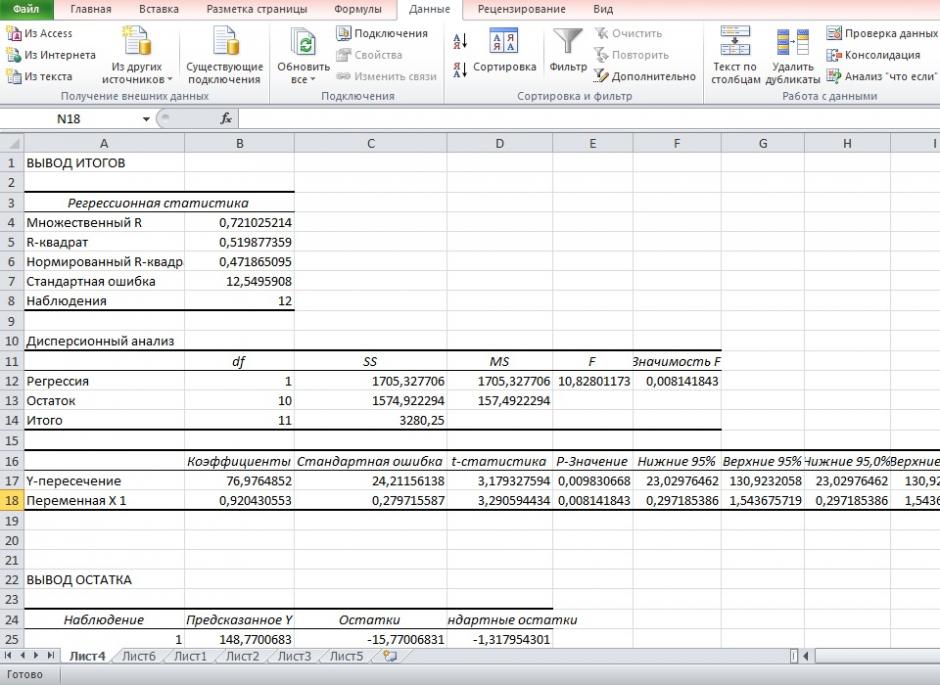
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
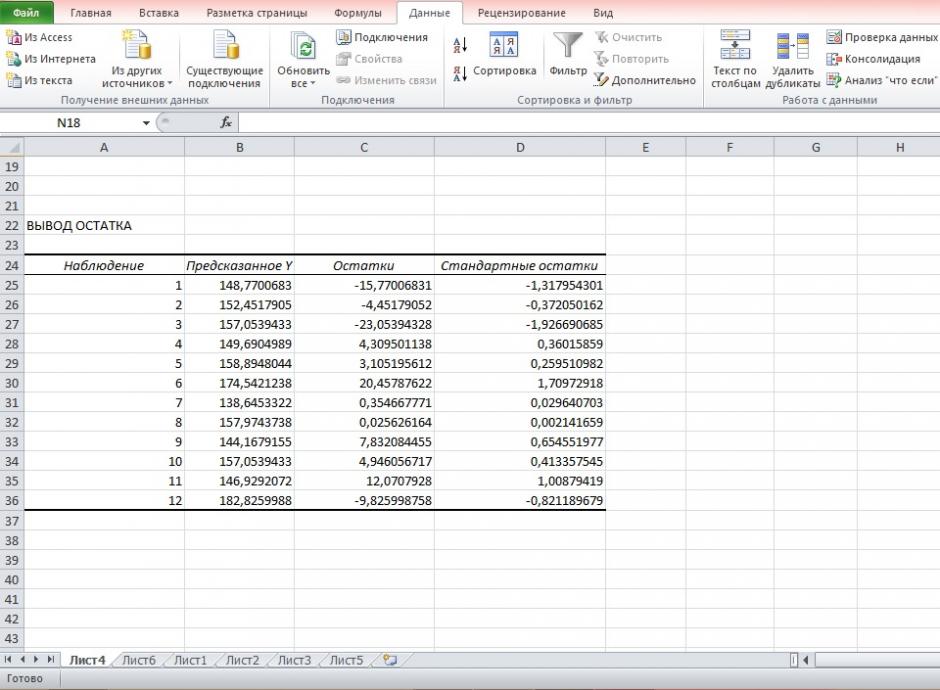
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
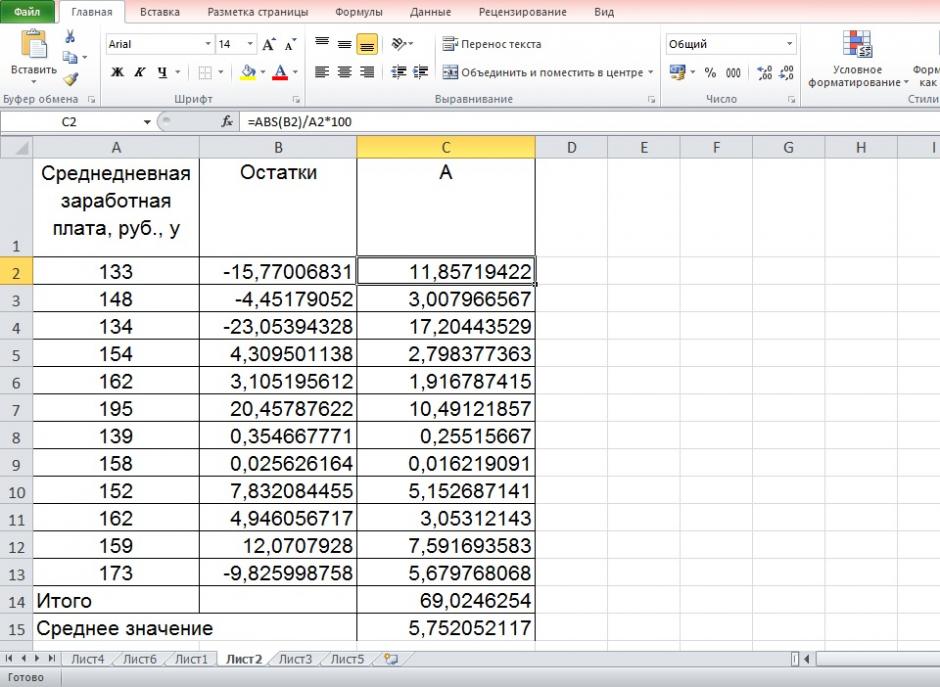
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как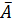 
не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: 
Поскольку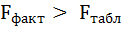 
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы 
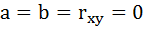
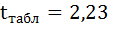
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 
где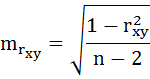 
– случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ: 
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью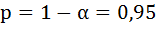 
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где 
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
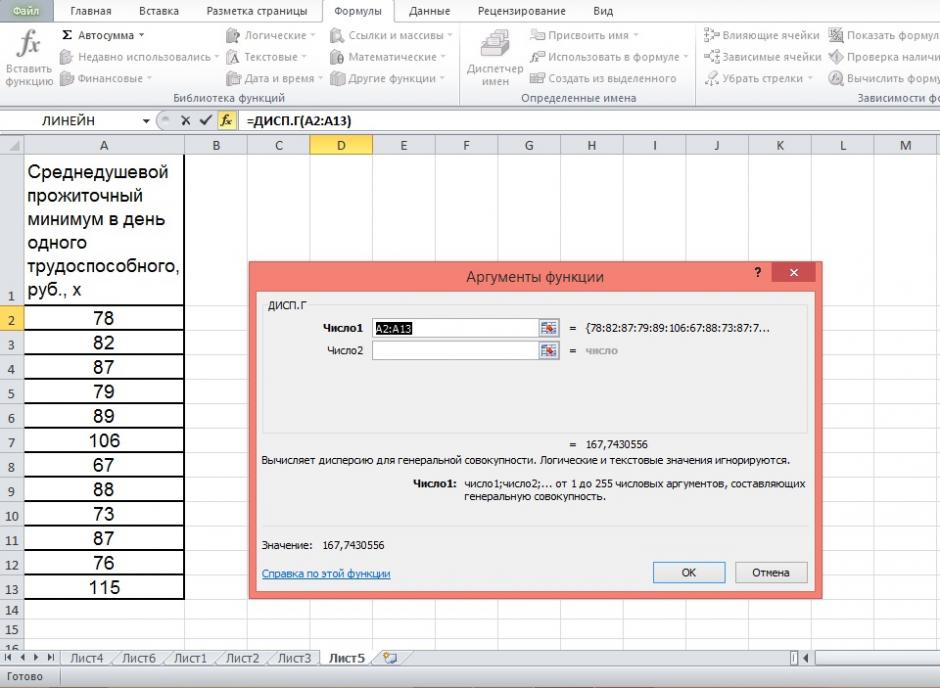
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии 
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при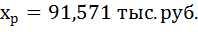 
с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
🔥 Видео
Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать
Эконометрика. Множественная регрессия и корреляция.Скачать
Эконометрика Линейная регрессия и корреляцияСкачать
Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать
Парная регрессия: линейная зависимостьСкачать
Эконометрика. Линейная парная регрессияСкачать
Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать
Что такое линейная регрессия? Душкин объяснитСкачать
Построение уравнения линейной регрессии методом наименьших квадратов.Скачать
Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать
Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать
Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать
Множественная регрессия в ExcelСкачать
Множественная регрессияСкачать
Линейная регрессияСкачать
Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать
Расчет коэффициента корреляции в ExcelСкачать
Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать
