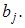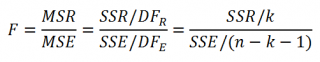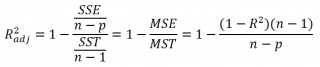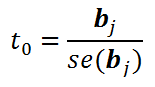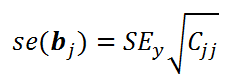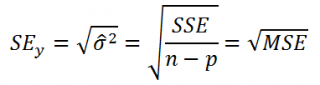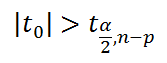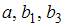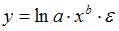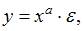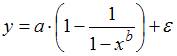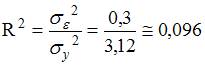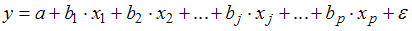на основании 14 наблюдений рассчитаны оценки параметров и записана модель: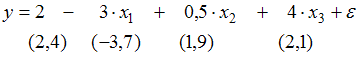
(в скобках указаны значения t-статистик, соответствующие параметрам регрессии). Известны критические значения Стьюдента при различных уровнях значимости
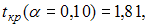
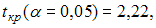
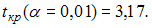
Для данного уравнения при уровне значимости
В нашем случае при уровне значимости 0,01 значимым является только параметр 
Эконометрика : учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М. : Финансы и статистика, 2005. – С. 160–170.
Кремер, Н.Ш. Эконометрика : учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко ; ред. Н. Ш. Кремер. – М. : ЮНИТИ, 2002. – С.40–52.
ответ тест i-exam
Видео:Множественная регрессия в ExcelСкачать
Подробный разбор задачи (примера) множественной регрессии в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Рассмотрим пример построения модели множественной регрессии в случае 2-х регрессоров в MS EXCEL.
Подробно модель множественной регрессии рассмотрена в соответствующей статье, которую рекомендуется прочитать перед разбором примера.
Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать
Условия задачи
Задача взята из англоязычного учебника «Introduction to Linear Regression Analysis», пятое издание, авторы D.C.Montgomery, E.A. Peck, G.G. Vining
Компания, осуществляющая услуги по обслуживанию торговых автоматов по продаже безалкогольных напитков, анализирует свою деятельность. Компания заинтересована в прогнозировании времени обслуживания одного автомата. Услуга включает доставку напитков до автомата, их размещение в автомат и уборку. Инженер, отвечающий за анализ, предположил, что две наиболее важные переменные, влияющие на время доставки ( Y ) являются: количество напитков, помещаемых в автомат (X1) и расстояние, которое водитель проезжает от склада до автомата (X2). Инженер собрал 25 наблюдений, которые приведены в таблице в файле примера на листе Модель . Для прогнозирования времени доставки необходимо построить модель множественной линейной регрессии.
Видео:Множественная регрессияСкачать
Оценка неизвестных параметров модели
Построение модели выполняется исключительно на основании значений наблюдений, приведенных в таблице B12: D 36 .
Коэффициенты множественной регрессии удобнее всего вычислить в MS EXCEL с помощью функции ЛИНЕЙН() , см. статью Функция MS EXCEL ЛИНЕЙН() . Для этого достаточно ввести формулу ЛИНЕЙН(D12:D36;B12:C36) . Ее нужно ввести как формулу массива (выделить 3 ячейки в строке и нажать CTRL + SHIFT + ENTER ).
Примечание : Коэффициенты регрессии вычисляются на основе метода МНК .
Расчет можно произвести также с помощью матричного подхода — одной формулой массива:
= МУМНОЖ( МОБР(МУМНОЖ(ТРАНСП(A12:C36);A12:C36)); МУМНОЖ(ТРАНСП(A12:C36);D12:D36) )
Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b=(X T X) -1 (X T Y) или в другом обозначении транспонированных матриц : b=(X ’ X) -1 (X ’ Y)
Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать
Диаграмма рассеяния
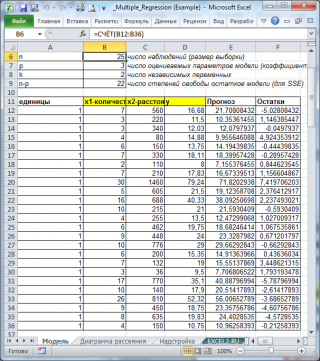
Матричная диаграмма рассеивания построена на листе Диаграмма рассеяния в файле примера .
Диаграмма рассеивания представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости. В этом случае удобно наблюдать разброс значений прогнозируемой переменной относительно плоскости регрессии.
Видео:Эконометрика. Построение модели множественной регрессии в Excel.Скачать
Вычисление прогнозных значений Y
В MS EXCEL прогнозное значение Y для заданных Х 1 и Х 2 можно предсказать с помощью функции ТЕНДЕНЦИЯ() :
или путем вычисления через уравнение регрессии:
Видео:Построение модели множественной регрессии в программе GretlСкачать
Тест на значимость Регрессии
Проверку значимости регрессии можно осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что тестовая статистика F примет значение F 0 (эта вероятность и есть p -значение ), затем сравнивают p -значение с заданным уровнем значимости . Если p -значение меньше уровня значимости , то имеются основания для отклонения нулевой гипотезы, и регрессия значима.
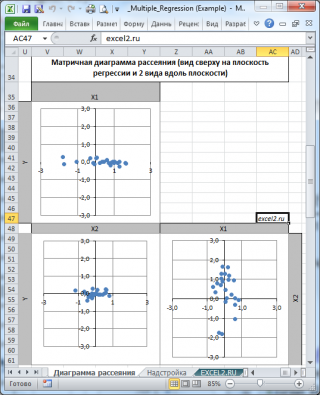
Значение F 0 вычисляется на основании значений выборки или через функцию ЛИНЕЙН() :
p -значение вычисляется по формуле
где, n – количество наблюдений (25), p – число оцениваемых параметров модели b (3), k- количество переменных Х (2).
Видео:09 Множественная регрессияСкачать
Коэффициент детерминации R 2
Коэффициент детерминации R 2 можно определить по формуле:
В регрессионном анализе также часто используют нормированный коэффициент детерминации (Adjusted R-squared):
Тест на значимость коэффициентов регрессии
Нулевая гипотеза состоит в том, что коэффициент регрессии bj равен 0. В этом случае тестовая статистика
имеет распределение Стьюдента с n-k-1 степенью свободы. При этом стандартная ошибка ( se – standard error ) коэффициента регрессии вычисляется по формуле:
C jj – соответствующий диагональный элемент матрицы (Х’X) -1 .
SEy – стандартная ошибка регрессии .
В MS EXCEL для вычисления стандартной ошибки коэффициента регрессии используется функция ЛИНЕЙН() . Например, для коэффициента b 0 формула будет иметь вид:
В файле примера стандартная ошибка коэффициента регрессии вычислена также впрямую — с использованием матричного подхода. В этом случае нам понадобится вычислить стандартную ошибку регрессии SEy . Ее также можно вычислить через функцию ЛИНЕЙН() :
Либо рассчитать через оценку дисперсии остатков модели (σ 2 ) по формуле:
Итак, вычислив значение тестовой статистики, его нужно сравнить с критическим значением, вычисленным для заданного уровня значимости альфа :
– квантиль распределения Стьюдента . В MS EXCEL вычисления квантиля производят по формуле = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) , подробнее см. в статье про распределение Стьюдента .
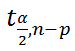
Мы имеем основание отклонить гипотезу Н 0 , если
Проверку гипотезы можно осуществить также через р-значение (вероятность того, что тестовая статистика примет значение |t 0 |):
Если через р-значение меньше уровня значимости , то гипотеза Н 0 отклоняется.
В файле примера на листе Надстройка приведены вычисления с помощью Надстройки Регрессия . Как и ожидалось, все показатели регрессии, вычисленные нами по формулам, совпадают с вычислениями Надстройки .
Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 
Найдем коэффициент детерминации: 
Вычислим коэффициент корреляции: 
2. Известно, что общая сумма квадратов отклонений 
, а остаточная сумма квадратов отклонений, 
. Тогда значение коэффициента детерминации равно …
Решение:
Для расчета коэффициента детерминации можно пользоваться следующей формулой: 
. Значит, в нашем случае коэффициент детерминации равен: 
3. Для регрессионной модели вида 
, где 
рассчитаны дисперсии: 
; 
; 
. Тогда величина 
характеризует долю …
Решение:
Значение коэффициента детерминации 
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность 
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле . Поэтому отношение характеризует долю остаточной дисперсии.
4. Если общая сумма квадратов отклонений 
, и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
Решение:
Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.
Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.
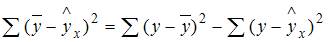
Получается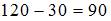 
.
Тема 11: Проверка статистической значимости эконометрической модели
1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 
, где …
n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число наблюдений
Решение:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
2. Если известно уравнение множественной регрессии 
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
Решение:
Расчет F-статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
, где
– общая сумма квадратов отклонений
– сумма квадратов отклонений, объясненная регрессией
– остаточная сумма квадратов отклонений
В нашем случае дано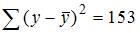 
, 
. Следовательно, 
Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:
n – 1 = m + (n – m – 1), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.
Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.
Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.
Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.
Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам 
F-статистика вычисляется по формуле 
3. Для регрессионной модели известны следующие величины дисперсий:
где y – значение зависимой переменной по исходным данным; 
– значение зависимой переменной, вычисленное по регрессионной модели; 
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
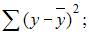
Решение:
Назовем приведенные дисперсии: 
– общая дисперсия; 
– объясненная дисперсия; 
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
Тема 12: Оценка значимости параметров эконометрической модели
1. Для уравнения множественной регрессии вида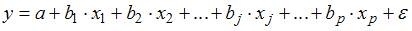 
на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
При уровне значимости 0,1 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии 
формулируется нулевая гипотеза 
при альтернативной гипотезе 
Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если 
, коэффициент 
значим; если 
коэффициент незначим. В нашем случае при уровне значимости 0,1 значимым является параметры 
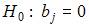
2. Если для среднеквадратической ошибки 
параметра и значения оценки этого параметра 
линейной эконометрической модели выполняется соотношение 
, то это свидетельствует о статистической ______ параметра.
ненадежности среднеквадратической ошибки
надежности среднеквадратической ошибки
Решение:
Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра.
3. Для уравнения множественной регрессии вида 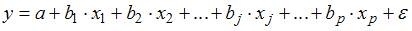на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры 
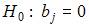
4. Проверка статистически значимого отличия от нуля оценок коэффициентов 
линейной модели
осуществляется путем последовательного сравнения отношений 
( 
–среднеквадратическая ошибка параметра ) с точкой, имеющей распределение …
Решение:
При проверке статистически значимого отличия от нуля оценок коэффициентов линейной регрессионной модели выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии 
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки . Полученное значение отношения последовательно сравнивается с точкой, имеющей распределение Стьюдента.
Тема 13: Нелинейные зависимости в экономике
1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.
2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе …
параболы второй степени
параболы третьей степени
Решение:
Параболу второй степени целесообразно применять в случае, когда на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную или обратная на прямую.
3. Нелинейное уравнение регрессии вида 
является _____ моделью ________ регрессии.
Решение:
Нелинейное уравнение регрессии вида является полиномиальной моделью парной регрессии. Теоретическое значение зависимой переменной рассчитывается в данном случае по формуле полинома третьей степени 
, а количество независимых переменных х равно единице.
4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.
Тема 14: Виды нелинейных уравнений регрессии
1. Степенной моделью не является регрессионная модель …
Решение:
Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: 
В уравнении независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.
2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.
3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне нелинейной, поскольку с помощью элементарных преобразований или замены переменных ее нельзя привести к линейному виду.
4. Среди предложенных нелинейных зависимостей внутренне линейной является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.
Тема 15: Линеаризация нелинейных моделей регрессии
1. Для линеаризации нелинейной регрессионной модели используется …
приведение уравнения к виду 1/y
Решение:
Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Нелинейная модель является степенной. Приведение ее к линейному виду возможно логарифмированием уравнения. Получаем 
Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель.
2. Для преобразования внутренне нелинейной функции может быть применен метод …
разложения функции в ряд Тейлора
Решение:
Функция является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.
3. Для линеаризации нелинейной функции может быть применен метод …
логарифмирования и замены переменных
разложения функции в ряд Тейлора
потенцирования и замены переменных
обращения и замены переменных
Решение:
Функция 
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду 
, которая является линейной относительно логарифмов переменных. Сделав замену переменных 
, 
, 
, 
, получим линейную функцию 
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
Тема 16: Оценка качества нелинейных уравнений регрессии
1. При расчете уравнения нелинейной регрессии 
, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …
Решение:
Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0,8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0,8; 1].
2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: 
. Коэффициент корреляции между логарифмами исходных показателей составил 
. Коэффициент детерминации для модели в исходных показателях равен …
Решение:
Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.
3. Для регрессионной модели 
, где 
– нелинейная функция, 
– рассчитанное по модели значение переменной 
, получены значения дисперсий: 
. Не объяснена моделью часть дисперсии переменной , равная …
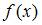
Решение:
Значение индекса детерминации R 2 характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R 2 ) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R 2 : 
. Следовательно, разность 
. Таким образом, часть дисперсии переменной , необъясненная моделью, равна 0,096. Можно также рассчитать это значение через отношение 
4. Для регрессионной модели , где – нелинейная функция, – рассчитанное по модели значение переменной , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной , равная …
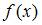
Решение:
Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R 2 . Значения индекса детерминации R 2 и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 
. Следовательно, значение 
.
5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии , где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2,05, а критические значения для данного количества степеней свободы равны 
, 
, 
, то …
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
Решение:
Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза 
при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент 
значим; если 
, коэффициент незначим. В нашем случае при уровне значимости коэффициент значим, а при уровнях значимости и незначим.
Тема 17: Временные ряды данных: характеристики и общие понятия
1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.
Решение:
Ряд, построенный по реальным данным, может не содержать тренда, сезонной (циклической) компоненты, однако, он обязательно содержит случайную компоненту.
2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
Решение:
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом.
4. Выраженную положительную тенденцию содержит ряд …
—
Решение:
Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t.
Тема 18: Структура временного ряда
1. Значение коэффициента автокорреляции первого порядка характеризует …
тесноту линейной связи
качество модели временного ряда
тесноту нелинейной связи
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.
📺 Видео
Эконометрика. Множественная регрессия и корреляция.Скачать
Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать
Множественная регрессия в программе SPSS (Multiple regression)Скачать
Множественная регрессия в программе Statistica (Multiple regression)Скачать
09 02 Основы множественной регрессииСкачать
Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать
Множественная Линейная Регрессия || Машинное ОбучениеСкачать
EViews. Урок 1. Построение модели множественной регрессии.Скачать
Эконометрика. Линейная парная регрессияСкачать
Часть 2. Множественная регрессия в Microsoft Excel. Автокорреляция, гетероскедастичность.Скачать
