ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
3.5 ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
3.5.1 Электрические потенциалы на фазовых границах
При соприкосновении проводника первого рода (электрода) с полярным растворителем (водой) либо раствором электролита на границе электрод – жидкость возникает т.н. двойной электрический слой (ДЭС). В качестве примера рассмотрим медный электрод, погруженный в воду либо в раствор сульфата меди.
При погружении медного электрода в воду часть ионов меди, находящихся в узлах кристаллической решетки, в результате взаимодействия с диполями воды будет переходить в раствор. Возникающий при этом на электроде отрицательный заряд будет удерживать перешедшие в раствор ионы в приэлектродном пространстве – образуется двойной электрический слой (рис. 3.12а; о моделях строения ДЭС смотрите п. 4.2.4). Отрицательный заряд на электроде будет препятствовать дальнейшему переходу ионов меди в раствор, и через некоторое время установится динамическое равновесие, которое можно однозначно охарактеризовать потенциалом электрического поля ДЭС Φ, зависящего от заряда на электроде, или некоторой равновесной концентрацией ионов в приэлектродном слое Сo. При погружении медного электрода в раствор СuSО4, содержащий ионы меди в концентрации С возможны три случая:
Рис. 3.12 Схема двойного электрического слоя на границе электрод-раствор
1. С Сo. Поскольку концентрация ионов меди в поверхностном слое больше равновесной, начнется переход ионов из раствора в электрод; на электроде возникает положительный заряд и в поверхностном слое преобладают анионы SО4 2- (рис. 3.12b).
3. С = Сo. Поскольку концентрация ионов меди в поверхностном слое равна равновесной (такие растворы называют нулевыми), заряд на электроде не возникает, двойной электрический слой не образуется.
3.5.2 Гальванический элемент. ЭДС гальванического элемента
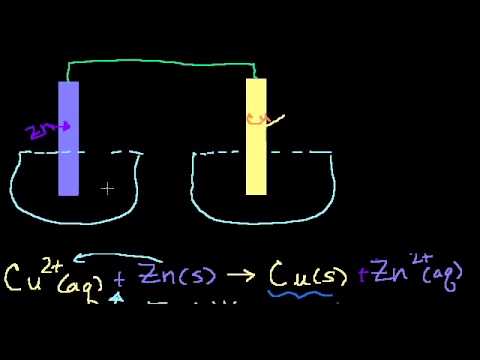
Рассмотрим простейший гальванический элемент Даниэля – Якоби, состоящий из двух полуэлементов – цинковой и медной пластин, помещенных в растворы сульфатов цинка и меди соответственно, которые соединены между собой посредством электролитического ключа – например, полоски бумаги, смоченной раствором какого-либо электролита. Схематически данный элемент изображается следующим образом:
Zn / Zn 2+ // Cu 2+ / Cu
На поверхности каждого из электродов имеет место динамическое равновесие перехода ионов металла из электрода в раствор и обратно, характеризуемое потенциалом ДЭС (зарядом на электроде q). Если соединить медный и цинковый электроды металлическим проводником, немедленно произойдет перераспределение зарядов – электроны начнут перемещаться с электрода с более отрицательным зарядом (в нашем случае – цинкового) на электрод с более положительным зарядом (медный), т.е. в проводнике возникнет электрический ток. Изменение величины заряда каждого из электродов нарушает равновесие – на цинковом электроде начнется процесс перехода ионов из электрода в раствор (окисление металла), на медном – из раствора в электрод (восстановление металла); при этом протекание процесса на одном электроде обусловливает одновременное протекание противоположного процесса на другом:
Электрод, на котором при работе гальванического элемента протекает процесс окисления, называется анодом , электрод, на котором идет процесс восстановления – катодом . При схематическом изображении гальванических элементов слева записывают анод, справа – катод (стандартный водородный электрод всегда записывают слева). Суммарный окислительно-восстановительный процесс, происходящий в гальваническом элементе, выражается следующим уравнением:
Т.о., гальванический элемент можно определить как прибор для преобразования химической энергии окислительно-восстановительной реакции в электрическую за счет пространственного разделения процессов окисления и восстановления. Работа, которую может совершить электрический ток, вырабатываемый гальваническим элементом, определяется разностью электрических потенциалов между электродами (называемой обычно просто разностью потенциалов) ΔΦ и количеством прошедшего по цепи электричества q:
(III.39)
Работа тока гальванического элемента (и, следовательно, разность потенциалов), будет максимальна при его обратимой работе, когда процессы на электродах протекают бесконечно медленно и сила тока в цепи бесконечно мала. Максимальная разность потенциалов, возникающая при обратимой работе гальванического элемента, есть электродвижущая сила (ЭДС) гальванического элемента .
3.5.3 Электродный потенциал. Уравнение Нернста
ЭДС гальванического элемента E удобно представлять в виде разности некоторых величин, характеризующих каждый из электродов – электродных потенциалов; однако для точного определения этих величин необходима точка отсчета – точно известный электродный потенциал какого-либо электрода. Электродным потенциалом электрода ε э называется ЭДС элемента, составленного из данного электрода и стандартного водородного электрода (см. ниже), электродный потенциал которого принят равным нулю. При этом знак электродного потенциала считают положительным, если в таком гальваническом элементе испытуемый электрод является катодом, и отрицательным, если испытуемый электрод является анодом. Необходимо отметить, что иногда электродный потенциал определяют как «разность потенциалов на границе электрод – раствор», т.е. считают его тождественным потенциалу ДЭС, что не вполне правильно (хотя эти величины взаимосвязаны).
Величина электродного потенциала металлического электрода зависит от температуры и активности (концентрации) иона металла в растворе, в который опущен электрод; математически эта зависимость выражается уравнением Нернста (здесь F – постоянная Фарадея, z – заряд иона):
(III.40)
В уравнении Нернста ε ° – стандартный электродный потенциал , равный потенциалу электрода при активности иона металла, равной 1 моль/л. Стандартные электродные потенциалы электродов в водных растворах составляют ряд напряжений. Величина ε ° есть мера способности окисленной формы элемента или иона принимать электроны, т.е. восстанавливаться. Иногда различием между концентрацией и активностью иона в растворе пренебрегают, и в уравнении Нернста под знаком логарифма фигурирует концентрация ионов в растворе. Величина электродного потенциала определяет направление процесса, протекающего на электроде при работе гальванического элемента. На полуэлементе, электродный потенциал которого имеет большее (иногда говорят – более положительное) значение, будет протекать процесс восстановления, т.е. данный электрод будет являться катодом.
Рассмотрим расчёт ЭДС элемента Даниэля – Якоби с помощью уравнения Нернста. ЭДС всегда является положительной величиной и равна разности электродных потенциалов катода и анода:
(III.41)
(III.42)
(III.43)
(III.44)
(III.45)
Как видно из уравнения (III.45), ЭДС элемента Даниэля – Якоби зависит от концентрации (точнее говоря, активности) ионов меди и цинка; при их равных концентрациях ЭДС элемента будет равна разности стандартных электродных потенциалов:
(III.46)
Анализируя уравнение (III.45), можно определить предел необратимой работы гальванического элемента. Поскольку на аноде идет процесс окисления цинка, концентрация ионов цинка при необратимой работе гальванического элемента постоянно увеличивается; концентрация ионов меди, напротив, уменьшается. Отношение концентраций ионов меди и цинка постоянно уменьшается и логарифм этого отношения при [Сu 2+ ] 2+ ] становится отрицательным. Т.о., разность потенциалов при необратимой работе гальванического элемента непрерывно уменьшается; при E = 0 (т.е. ε к = ε а) гальванический элемент не может совершать работу (необратимая работа гальванического элемента может прекратиться также и в результате полного растворения цинкового анода).
Уравнение (III.45) объясняет также и работоспособность т.н. концентрационных цепей – гальванических элементов, состоящих из двух одинаковых металлических электродов, опущенных в растворы соли этого металла с различными активностями а1 > а2. Катодом в этом случае будет являться электрод с большей концентрацией, т.к. стандартные электродные потенциалы обоих электродов равны; для ЭДС концентрационного гальванического элемента получаем:
(III.47)
Единственным результатом работы концентрационного элемента является перенос ионов металла из более концентрированного раствора в менее концентрированный. Т.о., работа электрического тока в концентрационном гальваническом элементе – это работа диффузионного процесса, который проводится обратимо в результате пространственного разделения его на два противоположных по направлению обратимых электродных процесса.
Copyright © С. И. Левченков, 1996 — 2005.
Видео:Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать
Зависимость ЭДС от концентрации. Уравнение Нернста
Величина гальвани-потенциала на границе металл-раствор электролита зависит от концентрации раствора согласно уравнению (10). Следовательно, от концентрации будет зависеть и условный потенциал такого электрода, а также ЭДС цепи, в которую он входит.
Согласно уравнению изотермы химической реакции для любой реакции, протекающей в гальваническом элементе, можно записать:
где К°а — константа равновесия реакции, выраженная через приведенные равновесные активности; Па — отношение произведения неравновесных приведенных активностей продуктов реакции, взятых в степенях, соответствующих стехиометрических коэффициентов, к аналогичному произведению неравновесных приведенных активностей исходных веществ. То есть для условной реакции
величина Па может быть записана как
Индекс # у активностей поставлен для того, чтобы подчеркнуть, что эти величины не относятся к равновесному состоянию системы. Таким образом, вычисление Па проводится по той же формуле, что и вычисление константы К°а , но в формулу подставляют неравновесные (начальные) значения относительных активностей участников реакции.
Учитывая (26), можно переписать (35) как 
откуда ЭДС гальванического элемента равна
Вспомним, что ЭДС называют стандартной и обозначают /г, если активности всех участников реакции равны единице. В этом случае Па — 1; 1пПа = 0, и уравнение (37) примет вид 
Таким образом, стандартная ЭДС гальванического элемента напрямую связана с константой равновесия реакции, протекающей в этом элементе. Зная величину стандартной ЭДС, можно вычислить константу равновесия:
Как вычислить величину стандартной ЭДС элемента Даниэля- Якоби по термодинамическим справочным данным?
Вычислим константу равновесия электродной реакции (17): 
Для этого выпишем значения AfG®98 для всех участников реакции:
Вычислим изменение функции Гиббса в ходе реакции:
Значение стандартной ЭДС совпадает с полученным ранее.
Учитывая уравнение (38), можно заменить первое слагаемое в (37) и получить следующее выражение для расчета ЭДС:
Выражение (40) называется уравнением Нернста.
Уравнение Нернста часто пишут в общем виде, для обобщенной реакции (20):
По решению Стокгольмской конвенции ШРАС (1953 г.) уравнение Нернста принято использовать со знаком «плюс», при этом числитель и знаменатель дроби, стоящей под логарифмом, меняются местами (в числителе будут активности исходных веществ, а в знаменателе — активности продуктов электродной реакции):
или 
Для элемента Даниэля-Якоби, учитывая реакцию (17), уравнение Нернста запишется в форме
Напомним, что химический потенциал чистого вещества равен его функции Гиббса, а активность чистого вещества равна единице. То
есть аСи =1 и aZn =1. (Также равной единице принимают и активность растворителя в разбавленном растворе). Поэтому
Таким образом, ЭДС элемента Даниэля-Якоби будет тем больше, чем больше концентрация раствора CuS04 и чем ниже концентрация ZnS04.
Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать
Применение уравнения Нернста в решении задач.
При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:
Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:
Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.
Пример 1:
Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO4 и 0.01М ZnSO4 соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.
Решение:
Для начала запишем уравнения протекающих процессов:
Далее находим по таблице стандартные потенциалы процессов:
Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.
Найдем реальные потенциалы с учетом нестандартных активностей ионов:
Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:
Ответ: 1.13 В
Пример 2:
Одним из лабораторных способов получения хлора является действие KMnO4 на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?
Решение:
Для начала запишем уравнения протекающих процессов.
Далее находим по таблице стандартные потенциалы процессов:
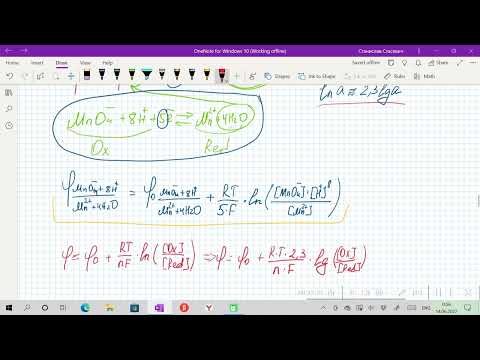
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:
Получается, что потенциал KMnO4 стал меньше, чем у хлора, а значит, реакция не пойдет.
🌟 Видео
Гальванические элементы. 1 часть. 10 класс.Скачать
011 Электрохимия 4 уравнение НернстаСкачать
Составление схемы и вычисление ЭДС гальванического концентрационного элемента | Уравнение НернстаСкачать
Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать
ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать
Уравнение НернстаСкачать
РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать
Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать
Задачи на гальванический элемент. Продукты в ОВР. Ч.5-4.Скачать
Электрохимия. Гальванический элемент Даниэля-ЯкобиСкачать
ОВР часть 2. Окислительно-восстановительные реакции. Электродный потенциал.Скачать
Гальванические элементыСкачать
Без этих теорем ты не затащишь геометрию на ЕГЭ. Задача 17 счетная планиметрияСкачать
Окислительно-восстановительные равновесия в аналитической химии.Скачать
Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать
Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать
8 класс. ОВР. Окислительно-восстановительные реакции.Скачать
