Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
- переменные являются коллинеарными;
- число уравнений равно числу анализируемых эндогенных переменных;
- переменные являются компланарными;
- число уравнений меньше числа анализируемых эндогенных переменных.
Временной ряд называется стационарным, если
- среднее значение членов ряда постоянно;
- члены ряда образуют арифметическую прогрессию;
- члены ряда образуют геометрическую прогрессию;
- среднее значение членов ряда постоянно растет.
18. Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями с:
- гомоскедастичными остатками;
- клонированными остатками;
- гетероскдастичными остатками;
- перпендикулярными остатками.
Одним из известных способов проверки регрессионных остатков эконометрической модели на автокорреляцию является критерий
Временной ряд называется стационарным, если
- среднее значение членов ряда постоянно;
- члены ряда образуют арифметическую прогрессию;
- члены ряда образуют геометрическую прогрессию;
- среднее значение членов ряда постоянно растет.
21. Внешние по отношению к рассматриваемой экономической модели переменные называются:
При анализе издержек Y от объема выпуска X целесообразно использовать сле-
- линейную;
- полиномиальную;
- логарифмическую;
- степенную;
- экспоненциальную.
23. Параметры 
- коэффициентами эластичности;
- бкоэффициентами корреляции;
- коэффициентами автокорреляции.
24. Коэффициент регрессии изменяется в пределах от:
- –1 до 1;
- 0 до 1;
- принимает любое значение.
На главной диагонали ковариационной матрицы в выражении
- дисперсии коэффициентов регрессии;
- средние значения коэффициентов регрессии;
- коэффициенты корреляции;
- квадраты коэффициентов корреляции.
При анализе производственной функции целесообразно использовать следующую
- линейную;
- полиномиальную;
- логарифмическую;
- степенную;
- экспоненциальную.
Значимость частных и парных коэффициентов корреляции проверяется с по-
- нормального закона распределения;
- t-критерия Стъюдента;
- F–критерия;
- таблицы Фишера – Иейтса.
28. В регрессионном анализе x j рассматриваются как:
- неслучайные величины;
- случайные величины;
- любые величины.
Для получения качественных оценок уравнений регрессии необходимо выполнение
следующих предпосылок МНК (выберите необходимые пункты):
- отклонения
должны быть нормально распределенными случайными вели-
- чинами с нулевым математическим ожиданием и постоянной дисперсией;
- отклонения
не должны коррелировать друг с другом;
- отклонения
должны иметь показательный закон распределения.
30. Коэффициент корреляции считается значимым с вероятностью ошибки 
Видео:Построение регрессионных моделей в R. Оценка точности и адекватности моделейСкачать

Проверка наличия предпосылок МНК
2. Вторая предпосылка МНК – нулевая средняя величина остатков, не зависящая от εi. Для проверки этой предпосылки строится график зависимости случайных остатков εi от факторов, включенных в регрессию xi.
Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xi. Если же график показывает зависимости εi от xi, то это свидетельствует о наличии систематической погрешности модели, причины которой могут быть разные.
Возможно, нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора xi. Может быть, неправильно подобрана модель.
Корреляция случайны остатков с факторными признаками, позволяет проводить корректировку модели, например, использовать кусочно-линейные модели.
3. В соответствии с третей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора xi остатки εi имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.
Проверка на наличие гетероскедастичности.
a) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной Xi, а по оси ординат квадраты отклонения εi 2 .
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии гетероскедастичности.
b) При помощи теста ранговой корреляции Спирмена.
4. При построение регрессионных моделей важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения остатков εi распределены независимо друг от друга.
Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент автокорреляции определяется по формуле линейного коэффициента корреляции: 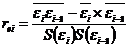
Пятая предпосылка МНК о нормальном распределении остатков может быть визуально проверена путем графического изображения ряда распределения остаточных величин и сравнения с кривой нормального распределения.
О соответствии эмпирического распределения теоретическому можно судить по величине эксцесса ( Е ≈0):
где М4 – центральный момент четвертого порядка, который определяется по формуле:
Рассчитать данные характеристики можно, воспользовавшись этим калькулятором.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Предпосылки метода наименьших квадратов
Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но сами оценки не позволяют сделать вывод, о том, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей совокупности, насколько близки оценки параметров b0 и b1 — коэффициентов к своим теоретическим значениям β0 и β1, как близко оцененное значение yi к условному математическому ожиданию M (Y(X = xi,), насколько надежны найденные оценки. Для ответа на эти вопросы нужны дополнительные исследования.
Значения yi зависят от значений xi и случайных отклонений εi. Значит, переменная Y является СВ, напрямую связанной с εi . До тех пор, пока не будет определенности в вероятностном поведении εi, мы не можем быть уверенными в качестве оценок.
Известно, что для получения по МНК наилучших результатов требуется, чтобы выполнялся ряд предпосылок относительно случайного отклонения.
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Предпосылки МНК (условия Гаусса-Маркова)
- Математическое ожидание случайного отклонения еi равно нулю: M(еi) = 0 для всех наблюдений.Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В определенном наблюдении случайный член может быть положительным или отрицательным, но он не должен иметь систематического смещения. Выполнимость M(еi) = 0 влечет выполнимость:
- Дисперсия случайных отклонений epsiloni постоянна: D(εi) = D (εj ) = σ 2 = const для любых наблюдений i и j.Условие независимости дисперсии ошибки от номера наблюдения называется гомоскедастичностью (homoscedasticity). Невыполнимость этой предпосылки называется гетероскедастичностью (heteroscedasticity).Поскольку D(ε)=M((εj — Mεj)) 2 = M(ε 2 ), то эту предпосылку можно переписать в форме: M(е 2 i) = σ 2 . Причины невыполнимости данной предпосылки и проблемы, связанные с этим, подробно рассматриваются ниже.
- Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.Выполнимость этой предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.Выполнимость данной предпосылки влечет следующее соотношение:
Если данное условие выполняется, то можно говорить об отсутствии автокорреляции. С учетом выполнимости предпосылки 1 данное соотношение можно переписать в виде:
Причины невыполнимости этой предпосылки и проблемы, связанные с ними, рассматриваются ниже.
- Случайное отклонение должно быть независимо от объясняющих переменных.Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в модели.Данное условие предполагает выполнимость следующего соотношения:
Заметим, что выполнимость этой предпосылки не столь критична для эконометрических моделей.
- Модель является линейной относительно параметров.Для случая множественной линейной регрессии существенными являются еще две предпосылки.
- Отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует сильная линейная зависимость.
- Случайные отклонения εi, i = 1, 2, … , n, имеют нормальное распределение.Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.
Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения. Например:
- объясняющие переменные не являются случайными величинами;
- число наблюдений намного больше числа объясняющих переменных (числа факторов уравнения);
- отсутствуют ошибки спецификации, т. е. правильно выбран вид уравнения и в него включены все необходимые переменные.
Зачастую полагают, что число наблюдений должно быть как минимум в 5-6 раз больше числа параметров уравнения (числа объясняющих переменных).
Задачи по эконометрике на предпосылки МНК решаются тут
🎦 Видео
Математика #1 | Корреляция и регрессияСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Уравнение множественной регрессии в ExcelСкачать

Эконометрика. Линейная парная регрессияСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Лекция 8. Множественная линейная регрессияСкачать

Множественная регрессия в ExcelСкачать

Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать

Парная линейная регрессионная модель. Эконометрика. Лабораторная работа №1. ExcelСкачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Как настроить агрегирование в BGP с атрибутами Aggregator и Atomic AggregateСкачать

Множественная регрессия в Excel и мультиколлинеарностьСкачать

РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Линейная регрессияСкачать

 должны быть нормально распределенными случайными вели-
должны быть нормально распределенными случайными вели-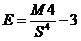
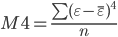
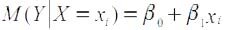
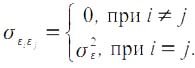 Если данное условие выполняется, то можно говорить об отсутствии автокорреляции. С учетом выполнимости предпосылки 1 данное соотношение можно переписать в виде:
Если данное условие выполняется, то можно говорить об отсутствии автокорреляции. С учетом выполнимости предпосылки 1 данное соотношение можно переписать в виде: 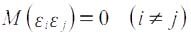 Причины невыполнимости этой предпосылки и проблемы, связанные с ними, рассматриваются ниже.
Причины невыполнимости этой предпосылки и проблемы, связанные с ними, рассматриваются ниже.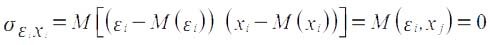 Заметим, что выполнимость этой предпосылки не столь критична для эконометрических моделей.
Заметим, что выполнимость этой предпосылки не столь критична для эконометрических моделей.