Для параболы найти координаты фокуса и уравнение директрисы онлайн (7 видео)

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Содержание

Калькулятор онлайн. Построение графика квадратичной функции.
Парабола
Парабола
Парабола, её форма, фокус и директриса.
Свойства параболы.
Уравнение касательной к параболе.
🎥 Видео

Видео:213. Фокус и директриса параболы.Скачать

Калькулятор онлайн.
Построение графика квадратичной функции.

Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.

Эта математическая программа для построения графика квадратичной функции сначала делает преобразование вида
( y=ax^2+cx+b ;; rightarrow ;; y=a(x+p)^2+q )
а затем последовательно строит графики функций:
$$ y=ax^2 $$
$$ y=a(x+p)^2+q $$

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5x +1/7x^2
Результат: ( 3frac — 5frac x + fracx^2 )

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

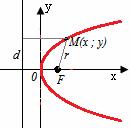
Парабола

Элементы параболы
0F — фокальная ось
0 — вершина
— фокус
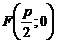
ε=1 — эксцентриситет
— фокальный радиус
— директриса
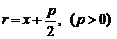
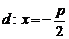
p — фокальный параметр

Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y 2 =2px
При p x 2 =2py
При p>0 ветви параболы направлены вверх, при p 2 /2+(y-1) 2 /2=1, необходимо набрать в поле x^2/2+(y-1)^2/2=1 и нажать кнопку График параболы .

Самостоятельно построить график можно, используя операцию выделения полного квадрата.

Видео:Фокус и директриса параболы 1Скачать

Парабола

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^=2pxlabel
$$
при условии (p > 0).

Из уравнения eqref вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

Рис. 8.11. Парабола.

Видео:Фокус и директриса параболы 2Скачать

Свойства параболы.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac

.label
$$

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^=(x-p/2)^+y^) и подставим сюда (y^) из канонического уравнения параболы. Мы получаем
$$
r^=left(x-frac

right)^+2px=left(x+frac

right)^.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac

.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt<left(x-frac

right)^+y^>=x+frac

.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_(x_, y_)), лежащей на ней. Пусть (y_ neq 0). Через точку (M_) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt) или же (y=-sqrt), смотря по знаку (y_).) Для функции (f(x)) выполнено тождество ((f(x))^=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_) и (f(x_)=y_), находим (f'(x_)=p/y_) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_=frac

<y_>(x-x_).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_^=2px_). Теперь уравнение касательной принимает окончательный вид
$$
yy_=p(x+x_).label
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_ neq 0), уравнение eqref превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref справедливо для любой точки на параболе.

Касательная к параболе в точке (M_) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке (M_(x_, y_)). Из уравнения eqref получаем ее направляющий вектор (boldsymbol(y_, p)). Значит, ((boldsymbol, boldsymbol_)=y_) и (cos varphi_=y_/boldsymbol). Вектор (overrightarrow<FM_>) имеет компоненты (x_=p/2) и (y_), а потому
$$
(overrightarrow<FM_>, boldsymbol)=x_y_-frac

y_+py_=y_(x_+frac

).nonumber
$$
Но (|overrightarrow<FM_>|=x_+p/2). Следовательно, (cos varphi_=y_/|boldsymbol|). Утверждение доказано.

Заметим, что (|FN|=|FM_|) (см. рис. 8.12).