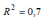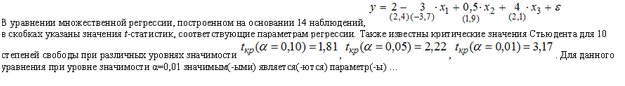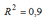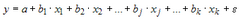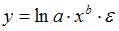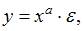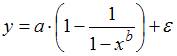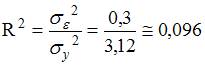Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
1. остатки автокоррелированны
2. средняя величина остатков не равна нулю
3. дисперсия остатков не является постоянной величиной
4. остатки гетероскедастичны
Вывод о присутствии в данном временном ряде сезонной компоненты можно сделать по значению коэффициента автокорреляции ____ порядка.
Нелинейная регрессионная модель отражает …
1. отсутствие связи между зависимой переменной и независимой переменной (независимыми переменными)
2. статистически незначимую нелинейную взаимосвязь между социально- экономическими показателями
3. совокупность линейных зависимостей между зависимой переменной и независимой переменной (независимыми переменными)
4. нелинейную взаимосвязь между социально-экономическими показателями
Для регрессионной модели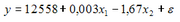 
зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
1. увеличится на 1,67
2. изменится на 0,003
3. уменьшится на (-1,67)
4. изменится на (-1,67)
Гиперболической моделью не является регрессионная модель …
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации R^2=0,6 . Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
При методе наименьших квадратов параметры уравнения парной линейной регрессии e=f+bx+e определяются из условия ______ остатков .
1. равенства нулю суммы квадратов
2. равенства нулю
3. минимизации суммы квадратов
4. минимизации модулей
Дана автокорреляционная функция временного ряда
1. имеет выраженную сезонную компоненту и имеет тенденцию
2. не имеет ни тенденции, ни сезонной компоненты
3. содержит только тенденцию, и не содержит сезонную компоненту
4. имеет выраженную сезонную компоненту и не имеет тенденции
Для регрессионной модели математическое ожидание остатков равно 0, следовательно, оценки параметров обладают свойством …
Если параметр эконометрической модели является статистически значимым, то отвергается статистическая гипотеза о том, что его значение …
1. равно коэффициенту парной корреляции Неверно
В модели множественной регрессии 
определитель матрицы парных коэффициентов корреляции между факторами х1, х2 и х3 близок к единице. Это означает, что факторы х1, х2 и х3 …
1. количественно измеримы
При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами …
1. несостоятельности, смещенности и эффективности
2. состоятельности, смещенности и эффективности
3. состоятельности, смещенности и неэффективности
4. состоятельности, несмещенности и эффективности
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации R^2. Тогда долю остаточной дисперсии зависимой переменной характеризует величина …
Для совокупности из n единиц наблюдений построена модель линейного уравнения множественной регрессии с количеством параметров при независимых переменных, равным k. Тогда при расчете объясненной дисперсии на одну степень свободы величину дисперсии относят к значению …
Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
2. сумма квадратов разности
3. квадрат разности
4. сумма разности квадратов
Значение коэффициента автокорреляции первого порядка характеризует …
1. значимость тренда
2. качество модели временного ряда
3. тесноту нелинейной связи
4. тесноту линейной связи
Если параметр эконометрической модели не является статистически значимым, то его значение признается …
2. отличным от 0
3. равным коэффициенту парной корреляции
Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент: S1=2, S2=-1, S3=-2.
Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда не формируют следующие значения компонент уровня временного ряда …
1. yt = 7; T = 3,5; S = 2; E = 1
2. yt = 7; T = 7; S = 1; E = 1
3. yt = 7; T = 3,5; S = -2; E = -1
4. yt = 7; T = -3,5; S = -2; E = -1
Гетероскедастичность можно обнаружить с помощью:
b. теста Дарбина-Уотсона
?d. теста Голфелда-Квандта
По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии
1. множественные и парные
2. линейные и нелинейные
3. линейные и парные
4. стохастические и вероятностные
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации, которое составило 
Следовательно, доля остаточной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
Если параметр эконометрической модели не является статистически значимым, то соответствующая независимая переменная …
1. не оказывает влияния на моделируемый показатель (зависимую переменную)
2. оказывает статистически значимое влияние на моделируемый показатель (зависимую переменную)
3. оказывает основное (доминирующее) влияние на зависимую переменную
4. тесно связан с зависимой переменной
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
При оценке статистической значимости построенной эконометрической модели выдвигают ______ гипотезы.
Для регрессионной модели несмещенность оценки параметра означает, что ее выборочное математическое ожидание равно …
1. коэффициенту парной корреляции между зависимой переменной и соответствующей независимой переменной
2. оцениваемому параметру, рассчитанному по генеральной совокупности
3. свободному члену уравнения регрессии
4. математическому ожиданию остатков модели
1. a, b1, b2, b3
Для совокупности из n единиц наблюдений рассчитывают общую дисперсию на одну степень свободы, при этом величину дисперсии относят к значению …
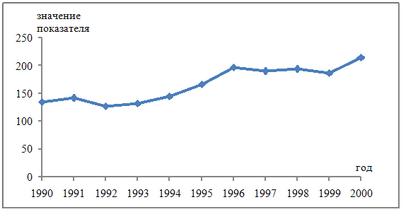
На графике изображен временной ряд, содержащий возрастающую тенденцию.
Исходя из данной структуры ряда можно предположить, что наиболее высокое значение коэффициента автокорреляции уровней ряда будет наблюдаться для ______ порядка.
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации 
Следовательно, доля остаточной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
Для регрессионной модели вида 
показателем тесноты связи является …
1. коэффициент множественной корреляции
2. коэффициент автокорреляции
3. F-критерий Фишера
4. парный коэффициент корреляции
Для регрессионной модели вида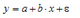 
построена на координатной плоскости совокупность точек с координатами (yi;xi), данное графическое отображение зависимости называется …
1. множественной регрессией
2. случайными факторами
3. полем корреляции
4. параметрами уравнения
При оценке параметров регрессионной модели с гетероскедастичными остатками при помощи обобщенного метода наименьших квадратов (ОМНК) выдвигается предположение, что дисперсия остатков …
2. пропорциональна некоторой величине
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
1. между несколькими временными рядами
2. между трендовой, сезонной и случайной компонентами
3. факторов, формирующих уровень ряда
4. первого, второго, третьего и последующих
Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …
1. экспоненциальной функции
2. степенной функции
3. параболы второй степени
4. равносторонней гиперболы
Ошибкой спецификации эконометрической модели уравнения регрессии является
1. расчет показателей качества модели
2. использование парной регрессии вместо множественной
3. оценка параметров при помощи МНК
4. учет случайных факторов
Одной из предпосылок метода наименьших квадратов является утверждение, что остатки регрессионной модели должны подчиняться _____ закону распределения.
Проверку статистической значимости построенной эконометрической модели на основе F-критерия осуществляют с использованием …
1. стандартизованных переменных
2. системы нормальных уравнений
3. статистических гипотез
4. коллективных гипотез
Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
1. дисперсия остатков не является постоянной величиной
2. средняя величина остатков не равна нулю
3. остатки гетероскедастичны
4. остатки автокоррелированны
Если оценка параметра является смещенной, то нарушается предпосылка метода наибольших квадратов о _____
1. случайном характере
2. нормальном законе распределения
3. нулевой средней величине
Временной ряд – это совокупность значений экономического показателя за несколько _____ моментов (периодов) времени.
Если известно уравнение множественной регрессии y=a+b1x1+b2x2+b3x3+e
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
Видео:МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 
Найдем коэффициент детерминации: 
Вычислим коэффициент корреляции: 
2. Известно, что общая сумма квадратов отклонений 
, а остаточная сумма квадратов отклонений, 
. Тогда значение коэффициента детерминации равно …
Решение:
Для расчета коэффициента детерминации можно пользоваться следующей формулой: 
. Значит, в нашем случае коэффициент детерминации равен: 
3. Для регрессионной модели вида 
, где 
рассчитаны дисперсии: 
; 
; 
. Тогда величина 
характеризует долю …
Решение:
Значение коэффициента детерминации 
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность 
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле . Поэтому отношение характеризует долю остаточной дисперсии.
4. Если общая сумма квадратов отклонений 
, и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
Решение:
Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.
Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.
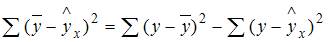
Получается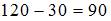 
.
Тема 11: Проверка статистической значимости эконометрической модели
1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 
, где …
n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число наблюдений
Решение:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
2. Если известно уравнение множественной регрессии 
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
Решение:
Расчет F-статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
, где
– общая сумма квадратов отклонений
– сумма квадратов отклонений, объясненная регрессией
– остаточная сумма квадратов отклонений
В нашем случае дано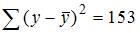 
, 
. Следовательно, 
Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:
n – 1 = m + (n – m – 1), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.
Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.
Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.
Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.
Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам 
F-статистика вычисляется по формуле 
3. Для регрессионной модели известны следующие величины дисперсий:
где y – значение зависимой переменной по исходным данным; 
– значение зависимой переменной, вычисленное по регрессионной модели; 
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
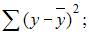
Решение:
Назовем приведенные дисперсии: 
– общая дисперсия; 
– объясненная дисперсия; 
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
Тема 12: Оценка значимости параметров эконометрической модели
1. Для уравнения множественной регрессии вида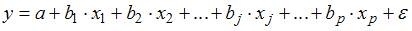 
на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
При уровне значимости 0,1 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии 
формулируется нулевая гипотеза 
при альтернативной гипотезе 
Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если 
, коэффициент 
значим; если 
коэффициент незначим. В нашем случае при уровне значимости 0,1 значимым является параметры 
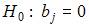
2. Если для среднеквадратической ошибки 
параметра и значения оценки этого параметра 
линейной эконометрической модели выполняется соотношение 
, то это свидетельствует о статистической ______ параметра.
ненадежности среднеквадратической ошибки
надежности среднеквадратической ошибки
Решение:
Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра.
3. Для уравнения множественной регрессии вида 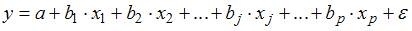на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры 
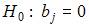
4. Проверка статистически значимого отличия от нуля оценок коэффициентов 
линейной модели
осуществляется путем последовательного сравнения отношений 
( 
–среднеквадратическая ошибка параметра ) с точкой, имеющей распределение …
Решение:
При проверке статистически значимого отличия от нуля оценок коэффициентов линейной регрессионной модели выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии 
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки . Полученное значение отношения последовательно сравнивается с точкой, имеющей распределение Стьюдента.
Тема 13: Нелинейные зависимости в экономике
1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.
2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе …
параболы второй степени
параболы третьей степени
Решение:
Параболу второй степени целесообразно применять в случае, когда на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную или обратная на прямую.
3. Нелинейное уравнение регрессии вида 
является _____ моделью ________ регрессии.
Решение:
Нелинейное уравнение регрессии вида является полиномиальной моделью парной регрессии. Теоретическое значение зависимой переменной рассчитывается в данном случае по формуле полинома третьей степени 
, а количество независимых переменных х равно единице.
4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.
Тема 14: Виды нелинейных уравнений регрессии
1. Степенной моделью не является регрессионная модель …
Решение:
Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: 
В уравнении независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.
2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.
3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне нелинейной, поскольку с помощью элементарных преобразований или замены переменных ее нельзя привести к линейному виду.
4. Среди предложенных нелинейных зависимостей внутренне линейной является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.
Тема 15: Линеаризация нелинейных моделей регрессии
1. Для линеаризации нелинейной регрессионной модели используется …
приведение уравнения к виду 1/y
Решение:
Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Нелинейная модель является степенной. Приведение ее к линейному виду возможно логарифмированием уравнения. Получаем 
Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель.
2. Для преобразования внутренне нелинейной функции может быть применен метод …
разложения функции в ряд Тейлора
Решение:
Функция является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.
3. Для линеаризации нелинейной функции может быть применен метод …
логарифмирования и замены переменных
разложения функции в ряд Тейлора
потенцирования и замены переменных
обращения и замены переменных
Решение:
Функция 
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду 
, которая является линейной относительно логарифмов переменных. Сделав замену переменных 
, 
, 
, 
, получим линейную функцию 
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
Тема 16: Оценка качества нелинейных уравнений регрессии
1. При расчете уравнения нелинейной регрессии 
, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …
Решение:
Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0,8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0,8; 1].
2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: 
. Коэффициент корреляции между логарифмами исходных показателей составил 
. Коэффициент детерминации для модели в исходных показателях равен …
Решение:
Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.
3. Для регрессионной модели 
, где 
– нелинейная функция, 
– рассчитанное по модели значение переменной 
, получены значения дисперсий: 
. Не объяснена моделью часть дисперсии переменной , равная …
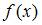
Решение:
Значение индекса детерминации R 2 характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R 2 ) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R 2 : 
. Следовательно, разность 
. Таким образом, часть дисперсии переменной , необъясненная моделью, равна 0,096. Можно также рассчитать это значение через отношение 
4. Для регрессионной модели , где – нелинейная функция, – рассчитанное по модели значение переменной , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной , равная …
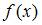
Решение:
Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R 2 . Значения индекса детерминации R 2 и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 
. Следовательно, значение 
.
5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии , где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2,05, а критические значения для данного количества степеней свободы равны 
, 
, 
, то …
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
Решение:
Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза 
при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент 
значим; если 
, коэффициент незначим. В нашем случае при уровне значимости коэффициент значим, а при уровнях значимости и незначим.
Тема 17: Временные ряды данных: характеристики и общие понятия
1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.
Решение:
Ряд, построенный по реальным данным, может не содержать тренда, сезонной (циклической) компоненты, однако, он обязательно содержит случайную компоненту.
2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
Решение:
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом.
4. Выраженную положительную тенденцию содержит ряд …
—
Решение:
Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t.
Тема 18: Структура временного ряда
1. Значение коэффициента автокорреляции первого порядка характеризует …
тесноту линейной связи
качество модели временного ряда
тесноту нелинейной связи
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.
Видео:Нелинейная регрессияСкачать
Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
📹 Видео
Эконометрика. Нелинейная регрессия. Степенная функция.Скачать
Коэффициент детерминации. Основы эконометрикиСкачать
Парная нелинейная регрессияСкачать
Лекции 14-15. Элементы теории корреляции. Уравнения регрессииСкачать
1.1 Нелинейная регрессия в ExcelСкачать
Эконометрика. Нелинейная регрессия. Полулогарифмические функции.Скачать
Математика #1 | Корреляция и регрессияСкачать
Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать
Эконометрика. Множественная регрессия и корреляция.Скачать
Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать
Множественная регрессия в ExcelСкачать
Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать
Эконометрика Линейная регрессия и корреляцияСкачать
Что такое линейная регрессия? Душкин объяснитСкачать
Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать
Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать
Занятие 6. Линейная регрессияСкачать
