Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Ваш ответ
Видео:Множественная регрессия в ExcelСкачать

решение вопроса
Видео:Множественная регрессияСкачать

Похожие вопросы
- Все категории
- экономические 43,408
- гуманитарные 33,633
- юридические 17,906
- школьный раздел 608,025
- разное 16,856
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Линейная множественная регрессия
Тесты по эконометрике
Введение
1. Эконометрическая модель имеет вид
2. Установите соответствие
| а) регрессионная модель | 1) x-1=0, x=0x-1, x>0 |
| b) система одновременных уравнений | 2) R=a1+b11M+b12Y+ε1,Y=a2+b21R+ε2, |
| c) модель временного ряда | 1. 3) y=a+b1x1+b2x2+ε |
| 4) yt=Tt+St+Et |
3. Регрессия – это
a. зависимость значений результативной переменной от значений объясняющих переменных (факторов)
b. правило, согласно которому каждому значению одной переменной ставится в соответствие единственное значение другой переменной
c. правило, согласно которому каждому значению независимой переменной ставится в соответствие значение зависимой переменной
d. зависимость среднего значения результативной переменной от значений объясняющих переменных (факторов)
4. Метод наименьших квадратов …
a. Позволяет получить оценки параметров линейной регрессии, исходя из условия i=1nyi-yi2→min
b. Позволяет получить оценки параметров регрессии, исходя из условия ln(i=1nf(yi,)→max
c. Позволяет проверить статистическую значимость параметров регрессии
d. Позволяет получить оценки параметров нелинейной регрессии, исходя из условия i=1ny-yi2→min
Линейная множественная регрессия
5. Уравнение линейной множественной регрессии
6. Для линейного уравнения множественной регрессии установите соответствие
| 5. а) Факторные переменные | 6. 1) y |
| 7. b) Результативная переменная | 8. 2) a |
| 9. c) Параметры | 10. 3) a, ε |
| 11. d) Случайная компонента | 12. 4) x1, x2 |
| 13. | 14. 5) ε |
| 15. | 16. 6) a, b1, b2 |
17. Ответ: a-4, b-1, c-6, d-5
7. Проблема спецификации регрессионной модели включает в себя
a. Отбор факторов, включаемых в уравнение регрессии
b. Оценка параметров уравнения регрессии
c. Оценка надежности результатов регрессионного анализа
d. Выбор вида уравнения регрессии
19. Требования к факторам, включаемым в модель линейной множественной регрессии…
a. Число факторов должно быть в 6 раз меньше объема совокупности
b. Факторы должны представлять временные ряды
c. Факторы должны иметь одинаковую размерность
d. Между факторами не должно быть высокой корреляции
21. Верные утверждения относительно мультиколлинеарности факторов
e. В модель линейной множественной регрессии рекомендуется включать мультиколлинеарные факторы
f. Мультиколлинеарность факторов приводит к снижению надежности оценок параметров уравнения регрессии
g. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, большими 0,7
h. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, меньшими 0,3
23. Верные утверждения о включении в уравнение линейной множественной регрессии факторов
i. Включение фактора в модель приводит к заметному возрастанию коэффициента множественной детерминации
j. Коэффициент парной корреляции для фактора и результативной переменной меньше 0,3
k. Значение t-критерия Стьюдента для коэффициента регрессии при факторе меньше табличного значения
l. Фактор должен объяснять поведение изучаемого показателя согласно принятым положениям экономической теории
25. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается модель с …
m. Одной объясняющей переменной, которая имеет с зависимой переменной наименьший коэффициент корреляции
n. Одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
o. Несколькими объясняющими переменными, которые имеют с зависимой переменной коэффициенты корреляции по модулю больше 0,5
p. Полным перечнем объясняющих переменных
8. Параметры при факторах в линейной множественной регрессии
y=a+b1x1+b2x2+…+bpxp характеризуют
a. Долю дисперсии результативной переменной, объясненную регрессией в его общей дисперсии
b. Тесноту связи между результативной переменной и соответствующим фактором, при устранении влияния других факторов, включенных в модель
c. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
d. На сколько процентов в среднем изменяется результативная переменная с изменением соответствующего фактора на 1%
28. Стандартизация переменных проводится по формуле
9. Уравнение множественной регрессии в стандартизованном масштабе имеет вид ty=20+0,9tx1+0,5tx2+ε. На результативный признак оказывает большое влияние:
x. нельзя сделать вывод
10. Уравнение множественной регрессии в естественной форме имеет вид
y=20+0,7×1+0,5×2+ε. На результативный признак оказывает большое влияние:
bb. нельзя сделать вывод
30. К свойствам уравнения регрессии в стандартизированном виде относятся …
cc. Коэффициенты регрессии при объясняющих переменных равны между собой
dd. Постоянный параметр (свободный член уравнения) регрессии отсутствует
ee. Стандартизированные коэффициенты регрессии несравнимы между собой
ff. Входящие в состав уравнения переменные являются безразмерными
32. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии оценивает
gg. Коэффициент парной корреляции
hh. Коэффициент частной корреляции
ii. Коэффициент множественной корреляции
jj. Коэффициент множественной детерминации
34. Установите соответствие
| 35. а) общая сумма квадратов отклонений TSS | 36. 1) y-y2 |
| 37. b) регрессионная сумма квадратов отклонений RSS | 38. 2) y-x2 |
| 39. c) остаточная сумма квадратов отклонений ЕSS | 40. 3) y-y2 |
| 41. | 42. 4) y-y2 |
43. Коэффициент множественной корреляции для линейной зависимости можно рассчитать по формуле
mm.
45. Верные утверждения относительно коэффициента множественной корреляции
oo. Чем ближе значение к единице Ryx1…xp, тем теснее связь результативного признака со всеми факторами
pp. Чем ближе значение к нулю Ryx1…xp, тем теснее связь результативного признака со всеми факторами
qq. Ryx1…xp принимает значения из промежутка [0, 1]
rr. Ryx1…xp принимает значения из промежутка [– 1, 1]
47. Коэффициент множественной детерминации характеризует
ss. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии
tt. Тесноту связи между результатом и соответствующим фактором, при устранении влияния других факторов, включенных в модель
uu. Долю дисперсии результативного признака, объясненную регрессией в его общей дисперсии
vv. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
49. Для общей (TSS), регрессионной (RSS) и остаточной (ESS) суммы квадратов отклонений и коэффициента детерминации R2 выполняется равенство …
51. Отношение остаточной дисперсии к общей дисперсии равно 0,05. Это означает …
bbb. Коэффициент детерминации R2=0,95
ccc. Коэффициент детерминации R2=0,05
ddd. Разность (1-R2)=0,95, где R2 – коэффициент детерминации
eee. Разность (1-R2)=0,05, где R2 – коэффициент детерминации
53. Для устранения систематической ошибки остаточной дисперсии для оценки качества модели линейной множественной регрессии используется
fff. Коэффициент множественной детерминации
ggg. Коэффициент множественной корреляции
hhh. Скорректированный коэффициент множественной детерминации
iii. Скорректированный коэффициент частной корреляции
55. Оценка статистической значимости уравнения линейной множественной регрессии в целом осуществляется с помощью
jjj. Критерия Стьюдента
kkk. Критерия Фишера
lll. Критерия Дарбина-Уотсона
56. Оценка статистической значимости коэффициентов линейной множественной регрессии осуществляется с помощью
nnn. Критерия Стьюдента
ooo. Критерия Фишера
ppp. Критерия Дарбина-Уотсона
qqq. Критерия Фостера-Стюарта
57. Если коэффициент регрессии является существенным, то для него выполняются условия
rrr. Фактическое значение t-критерия Стьюдента меньше критического
sss. Фактическое значение t-критерия Стьюдента больше критического
ttt. Доверительный интервал проходит через ноль
uuu. Стандартная ошибка не превышает половины значения параметра
59. Если уравнение регрессии является существенным, то фактическое значение F-критерия …
vvv. больше критического
www. меньше критического
xxx. близко к единице
yyy. близко к нулю
61. Предпосылками МНК являются…
zzz. Дисперсия случайных отклонений постоянна для всех наблюдений
aaaa. Дисперсия случайных отклонений не постоянна для всех наблюдений
bbbb. Случайные отклонения коррелируют друг с другом
cccc. Случайные отклонения являются независимыми друг от друга
63. Укажите выводы, которые соответствуют графику зависимости остатков
dddd. Нарушена предпосылка МНК о независимости остатков друг от друга
eeee. Имеет место автокорреляция остатков
ffff. Отсутствует закономерность в поведении остатков
gggg. Отсутствует автокорреляция остатков
66. При выполнении предпосылок метода наименьших квадратов (МНК) остатки уравнения регрессии, как правило, характеризуются…
hhhh. Нулевой средней величиной
jjjj. Случайным характером
kkkk. Высокой степенью автокорреляции
68. К методам обнаружения гетероскедастичности остатков относятся
llll. Критерий Дарбина-Уотсона
mmmm. Тест Голдфелда-Квандта
nnnn. Графический анализ остатков
oooo. Метод наименьших квадратов
70. Фиктивными переменными в уравнении множественной регрессии являются …
pppp. Качественные переменные, преобразованные в количественные
qqqq. Переменные, представляющие простейшие функции от уже включенных в модель переменных
rrrr. Дополнительные количественные переменные, улучшающие решение
ssss. Комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
71. Для отражения влияния качественной сопутствующей переменной, имеющей m состояний, обычно включают в модель … фиктивную переменную
Нелинейная регрессия
72. Регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам
73. Регрессии, нелинейные по оцениваемым параметрам
74. Укажите верные утверждения по поводу модели
jjjjj. Относится к типу моделей нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам
kkkkk. Относится к типу моделей, нелинейных по оцениваемым параметрам
lllll. Относится к типу линейных моделей
mmmmm. Нельзя привести к линейному виду
nnnnn. Можно привести к линейному виду
76. Укажите верные утверждения по поводу модели
ooooo. Линеаризуется линейную модель множественной регрессии
ppppp. Линеаризуется линейную модель парной регрессии
qqqqq. Относится к классу нелинейных моделей по объясняющим переменным, но линейных по оцениваемым параметрам
rrrrr. Относится к классу линейных моделей
79. Модель y=a∙bx∙ε относится к классу … эконометрических моделей нелинейной регрессии
81. Модель y=a∙xb∙ε относится к классу … эконометрических моделей нелинейной регрессии
83. Модель y=a+bx+cx2+ε относится к классу … эконометрических моделей нелинейной регрессии
85. Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии…
87. Для получения оценок параметров степенной регрессионной модели y=a∙xb …
iiiiii. Метод наименьших квадратов неприменим
jjjjjj. Требуется подобрать соответствующую подстановку
kkkkkk. Необходимо выполнить логарифмическое преобразование
llllll. Необходимо выполнить тригонометрическое преобразование
89. С помощью метода наименьших квадратов нельзя оценить значения параметров уравнения регрессии …
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Составить уравнение множественной линейной регрессии y = a + b1x1 + b2x2 + ε в матричной форме
Составить уравнение множественной линейной регрессии y = a + b1x1 + b2x2 + ε в матричной форме, используя МНК, и найти числовые характеристики переменных.
Найти оценки параметров а, b1, b2, б².
Найти коэффициент детерминации и оценить уравнение регрессивной связи.
Построить корреляционную матрицу и оценить статистическую зависимость между переменными.
По данным, полученным от фермерских хозяйств одного из регионов, изучается зависимость объёма выпуска продукции растениеводства Y (млн руб.) от двух факторов: численности работников Х1 (чел.) и количества осадков в период вегетации Х2 (мм).
№ п/п Y Х1 Х2
1 0.9 54 5
2 1.3 62 7
3 2.4 80 13
4 2.6 83 11
5 3.2 98 18
Тогда .
Рассчитаем
11111546280839857131118∙15451627180131831119818=537754377296534421544421688
11111546280839857131118∙0,91,32,42,63,2=10,4850,6131.
Матрицу определим по формуле , где – определитель матрицы ; – матрица, присоединенная к матрице
Получим
A-1=26,2174-0,63222,0047-0,63220,0160-0,05352,0047-0,05350,1879.
Теперь умножим эту матрицу на вектор
10,4850,6131
Получим B=26,2174-0,63222,0047-0,63220,0160-0,05352,0047-0,05350,1879∙10,4850,6131=-2,47590,0668-0,0444.
e=e1e2e3e4e5=-0,0084-0,05390,11050,0213-0,0696
2.Найдем оценки параметров а, b1, b2, б².
Исходя из матрицы В=-2,47590,0668-0,0444 значения параметров а=-2,4759,
b1=0,0668; b2=-0,0444.
Уравнение множественной регрессии имеет вид:
.
3.Найдем коэффициент детерминации и оценим уравнение регрессивной связи.
Для удобства вычислений составим вспомогательную таблицу.
№ х12
х2 2
у2
1 0.9 54 5 0.9084 1.3924 1.373 0.000 2916 25 0.81
2 1.3 62 7 1.3539 0.6084 0.527 0.003 3844 49 1.69
3 2.4 80 13 2.2895 0.1024 0.044 0.012 6400 169 5.76
4 2.6 83 11 2.5787 0.2704 0.249 0.000 6889 121 6.76
5 3.2 98 18 3.2696 1.2544 1.415 0.005 9604 324 10.24
SYMBOL 83f “symbol” * MERGEFORMAT 10.4 377 54 10.4 3.628 3.608 0.020 29653 688 25.26
Ср.знач. 2.08 75.4 10.8 5930.6 137.6 5.052
Рассчитаем коэффициент детерминации:
Коэффициент детерминации свидетельствует о том, что вариация исследуемой зависимой переменной на 99,4% объясняется изменчивостью включенных в модель объясняющих переменных , .
Рассчитаем скорректированный коэффициент детерминации:
Оба коэффициента детерминации свидетельствуют о сильной связи между факторными переменными и результативным показателем.
Проверим статистическую значимость на основе критерия Фишера по формуле:
Фактическое значение критерия F меньше табличного , определенного на уровне значимости при и степенях свободы, т.е. уравнение регрессии статистически незначимо, следовательно, исследуемая зависимая переменная Y плохо описывается включенными в регрессионную модель переменными.
4.Построим корреляционную матрицу и оценим статистическую зависимость между переменными.
Рассчитаем стандартизированные коэффициенты регрессии , коэффициенты эластичности , и -коэффициенты.
Коэффициент эластичности рассчитывается по формуле
;.
Это означает, что увеличение переменной на 1% (от своего среднего значения) приводит в среднем к росту величины на 2,422%, увеличение переменной на 1% (от своего среднего значения) приводит в среднем к уменьшению величины на 0,230%.
Стандартизированный коэффициент регрессии рассчитывается по формуле
,
где
,.
Стандартизированный коэффициент регрессии показывает, на сколько величин изменится в среднем зависимая переменная при увеличении только j-ой объясняющей переменной на .
Таким образом, увеличение только на одно увеличивает в среднем зависимую величину Y на 1,228; увеличение только на одно уменьшает в среднем зависимую величину Y на 0,239.
Рассчитаем -коэффициенты:
,
где – коэффициент парной корреляции.
Найдем матрицу коэффициентов парной корреляции.
это означает, что на 123,0% приращение величины Y можно объяснить влиянием изменения фактора ,
это означает, что на 23,0% приращение величины Y можно объяснить влиянием изменения фактора .
user969511 5.0
Два высших образования (менеджмент в информационных технологиях, автоматизация технологических процессов).+аспирант философского факультета и лингвистики. Стаж: больше 5 лет работы над рефератами,докладами,решениями тех,лингв и эконом задач
📹 Видео
Парная регрессия: линейная зависимостьСкачать

Линейная регрессияСкачать

Линейная регрессияСкачать

Лекция 2.1: Линейная регрессия.Скачать

Множественная линейная регрессия, часть 1Скачать

Множественная линейная регрессия, часть 2Скачать

Множественная степенная регрессияСкачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Эконометрика. Построение модели множественной регрессии в Excel.Скачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Что такое линейная регрессия? Душкин объяснитСкачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Множественная регрессия в MS Excel. Быстрое решение. И подробное решение. Калькулятор!Скачать
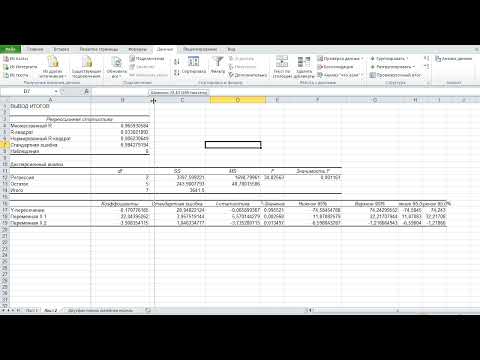
Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Множественная линейная регрессия в StatisticaСкачать


