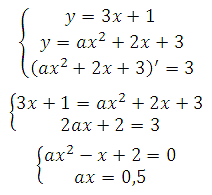Для каждого уравнения укажите прямую которую задает это уравнение у 1 3х 1 (7 видео)

Прямая у=3х+1 является касательной

119972. Прямая у=3х+1 является касательной к графику функции ах 2 +2х+3. Найдите a.

Прямая и график данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения.

Известно, что производная функции в данной точке равна угловому коэффициенту касательной y=kx+b (k угловой коэффициент), то есть f′(x₀)=k. Это третье уравнение:

Подставим ax из второго уравнения в первое, получим:

Найдём а, подставим х=4 в ах 2 –х+2=0:

По смыслу задачи параметр a≠0, график заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах 2 +2х+3=3х+1 имело единственное решение:

Квадратное уравнение будет иметь единственное решение, когда дискриминант будет равен нулю:

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Прямая линия. Уравнение прямой.

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

прямые пересекаются;

прямые параллельны;

прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных

Уравнение прямой по точке и вектору нормали.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой , заданной уравнением

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор (α₁, α₂), компоненты которого удовлетворяют условию

Аα₁ + Вα₂ = 0 называется направляющим вектором прямой.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем, то получим

xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Практика. Решение задач. Часть 1. Уравнения прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.