О чем эта статья:
- Основные определения
- Задача 1
- График зависимости скорости от времени при равноускоренном движении
- Задача 2
- Перемещение при равноускоренном движении
- Задача 3
- Графики равноускоренного движения
- Урок математики по теме «Применение интеграла к решению физических задач»
- Презентация к уроку
- Перемещение и путь при равноускоренном прямолинейном движении
- теория по физике 🧲 кинематика
- Перемещение при разгоне и торможении тела
- Этап торможения
- Этап разгона
- Перемещение в n-ную секунду прямолинейного равноускоренного движения
- Проекция и график перемещения
- График пути
- 📸 Видео
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Основные определения
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.
Несколько примеров равноускоренного движения:
разгон самолета перед взлетом;
торможение лыжника на горном склоне;
свободное падение в результате прыжка с парашютом;
велосипедист, спускающийся с горки;
мальчишки, играющие в догонялки.
Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Формула ускорения при равноускоренном движении
где a — ускорение тела [м/с 2 ],
V — мгновенная скорость [м/с],
V0 — начальная скорость [м/с],
t — время [с].
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:
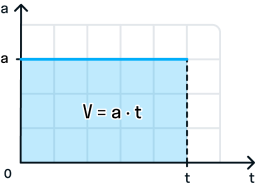
При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:
V(t) = V0 + at,
где V(t) — скорость в момент времени t [м/с],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Задача 1
Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с 2 ?
Решение.
По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:
V(10) = 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10 с Арсений разгонится до скорости 11 м/с.
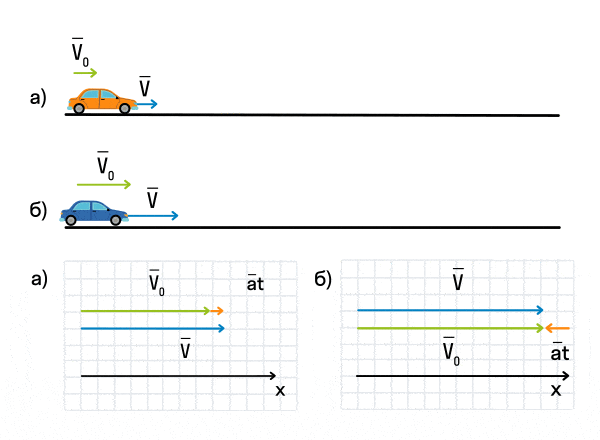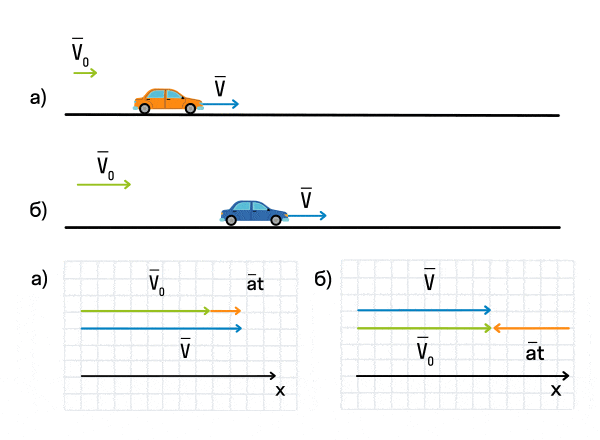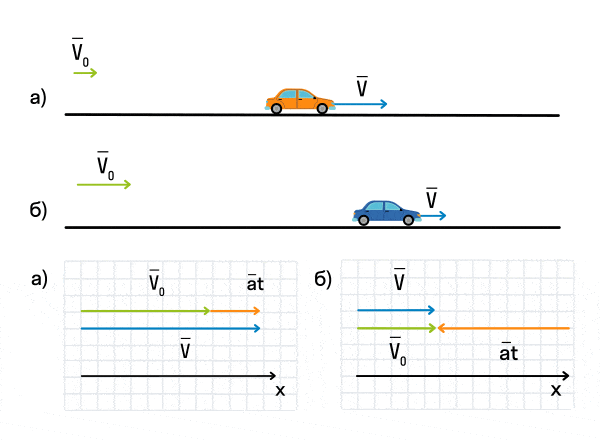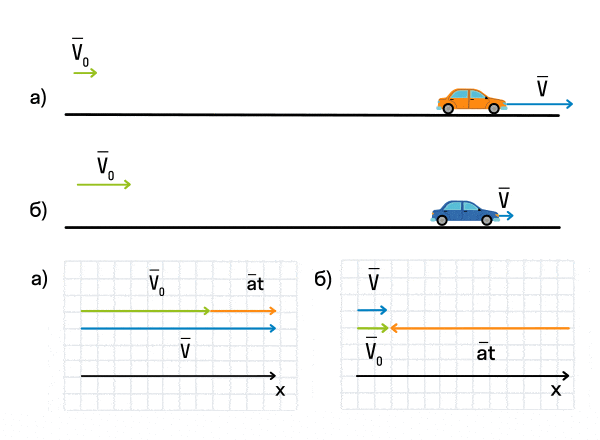
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.
Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.
Видео:Расчёт пути и времени движения | Физика 7 класс #12 | ИнфоурокСкачать

График зависимости скорости от времени при равноускоренном движении
Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V0).
При равнозамедленном движении прямая на графике будет убывать.
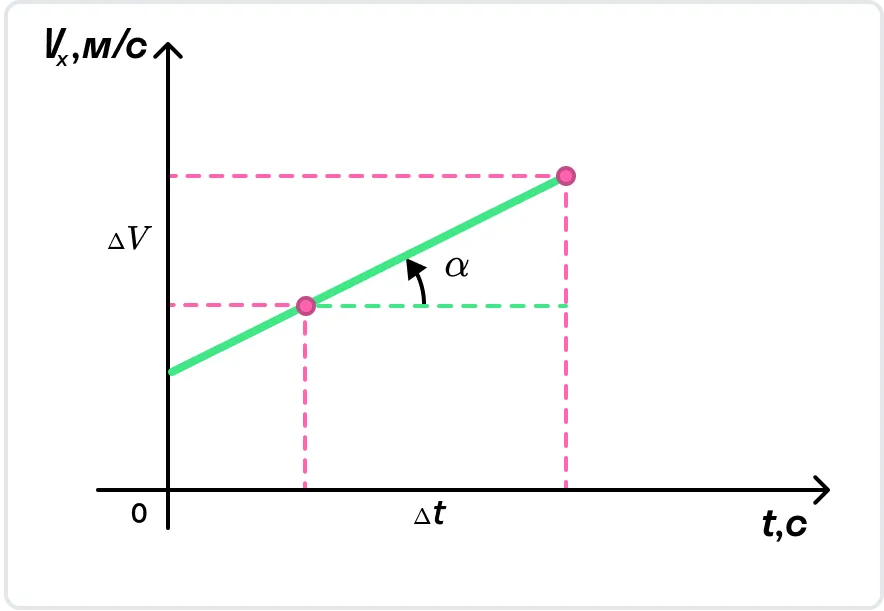
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:
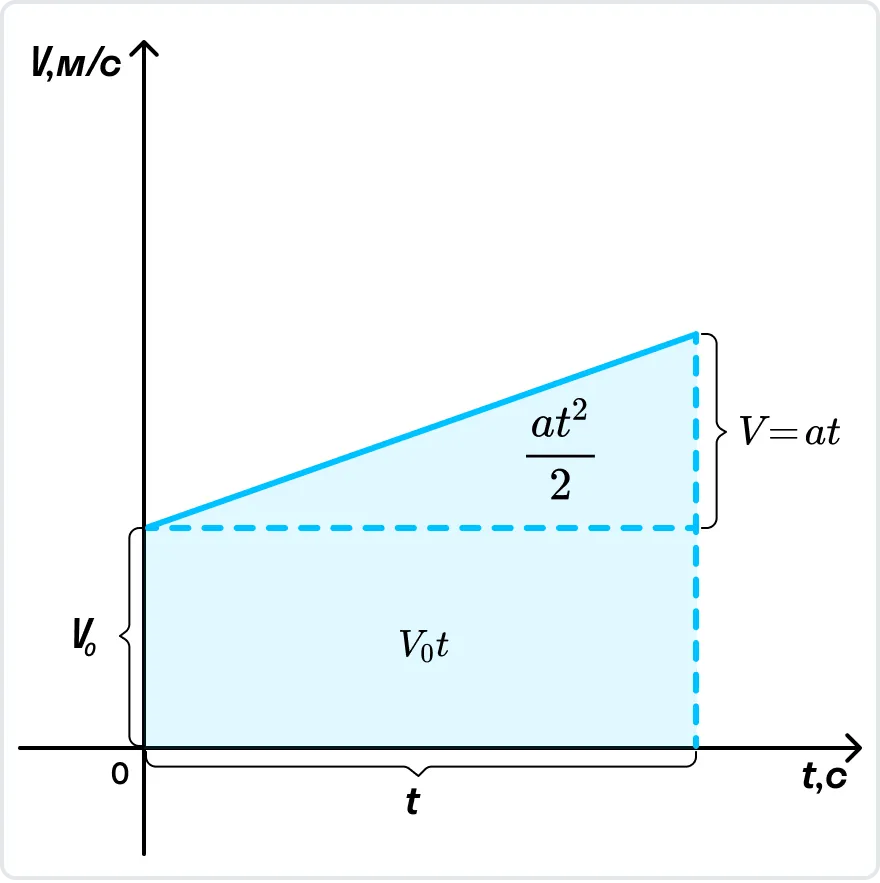
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V0t и треугольника .
Формула пути при равноускоренном движении
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с 2 ].
Задача 2
Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с 2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?
Решение.
По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
Поскольку время движения неизвестно, то определим путь по второй формуле:
Подставим числа и выполним расчет:
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Видео:Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.
Например, на этом графике путь тела равен S1 + S2, а перемещение — S1 − S2.
Уравнение перемещения при равноускоренном движении
,
где S — перемещение за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.
Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).
Уравнение равноускоренного движения
,
где x(t) — координата в момент времени t [м],
x0 — начальная координата [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.
Решение.
Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0 = 3 м/с. Начальная координата равна нулю.
Найдем ускорение из формулы пути при равноускоренном движении:
Составим уравнение движения лыжника:
По уравнению определим координату лыжника в момент времени t = 2 с:
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Графики равноускоренного движения
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.
Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Урок математики по теме «Применение интеграла к решению физических задач»
Презентация к уроку
Цель урока:
- обобщить и закрепить ключевые задачи по теме;
- научиться работать с теоретическими вопросами темы;
- научиться применять интеграл к решению физических задач.
План урока:
1. Схема решения задач на приложения определенного интеграла
2. Нахождение пути, пройденного телом при прямолинейном движении
3. Вычисление работы силы, произведенной при прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение или сжатие пружины
5. Определение силы давления жидкости на вертикально расположенную пластинку
Тип урока: интегрированный.
Воспитательная работа: расширение кругозора и познавательной деятельности учащихся, развитие логического мышления и умения применять свои знания.
Техническое обеспечение: интерактивная доска. Компьютер и диск.
Приложение: «Рапсодия природы».
I. Организационный момент
II. Постановка цели урока
– Урок хотелось бы провести под девизом Готфрида Вильгельма Лейбница – немецкого философа, логика, математика, физика: «Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли».
III. Повторим основные понятия и ответим на вопросы:
– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с применением интеграла?
IV. Объяснение нового материала (рассмотрение теории):
1. Схема решения задач на приложения определенного интеграла
С помощью определенного интеграла можно решать различные задачи физики, механики и т. д., которые трудно или невозможно решить методами элементарной математики.
Так, понятие определенного интеграла применяется при решении задач на вычисление работы переменной силы, давления жидкости на вертикальную поверхность, пути, пройденного телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т. д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через Х, а промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка. На каждой такой части задачу решают по формулам для постоянных величин.
Далее составляют сумму (интегральную сумму), выражающую приближенное значение искомой величины. Переходя к пределу при 
I = 
2. Нахождение пути, пройденного телом при прямолинейном движении
Как известно, путь, пройденный телом при равномерном движении за время t, вычисляется по формуле S = vt.
Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени t, т. е. v = f(t), то для нахождения пути, пройденного телом за время от 



Если функция v(t) непрерывна, то
Итак,
3. Вычисление работы силы, произведенной при прямолинейном движении тела
Пусть тело под действием силы F движется по прямой s, а направление силы совпадает с направлением движения. Необходимо найти работу, произведенную силой F при перемещении тела из положения a в положение b.
Если сила F постоянна, то работа находится по формуле 
Пусть на тело, движущееся по прямой Ох, действует сила F, которая изменяется в зависимости от пройденного пути, т. е. 


Составим интегральную сумму, которая приближенно равна значению произведенной работы:
т.е. работа, совершенная этой силой на участке от а до b, приближенно мала сумме:
Итак, работа переменной силы вычисляется по формуле:
4. Вычисление работы, затраченной на растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для растяжения или сжатия пружины, пропорциональна величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия пружины. Тогда 
Работа на участке 




Для нахождения истинной величины работы следует перейти к пределу
5. Определение силы давления жидкости на вертикально расположенную пластинку
Из физики известно, что сила Р давления жидкости на горизонтально расположенную площадку S, глубина погружения которой равна h, определяется по формуле:
, где
– плотность жидкости.
Выведем формулу для вычисления силы давления жидкости на вертикально расположенную пластинку произвольной формы, если ее верхний край погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки находятся на разной глубине, то сила давления жидкости на них неодинаковa. Для вывода формулы нужно разделить пластинку на горизонтальных полос одинаковой высоты 
По закону Паскаля сила давления жидкости на такую полосу равна силе движения жидкости на горизонтально расположенную пластинку той же площади, погруженной на ту же глубину.
Тогда согласно формуле (4) сила давления на полосу, находящуюся на расстоянии х от поверхности, составит 

Составим интегральную сумму и найдем ее предел, равный силе давления жидкости на всю пластинку:
Если верхний край пластинки совпадает с поверхностью жидкости, то а=0 и формула (5) примет вид
Ширина каждой полосы зависит от формы пластинки и является функцией глубины х погружения данной полосы.
Для пластинки постоянной ширины формула (5) упрощается, т.к. эту постоянную можно вынести за знак интеграла:
V. Разбор задач по теме
1) Скорость движения материальной точки задается формулой 

2) Скорость движения изменяется по закону 
3) Скорость движения тела задана уравнением 
Скорость движение тела равна нулю в момент начала его движения и остановки. Найдем момент остановки тела, для чего приравняем скорость нулю и решим уравнение относительно t; получим
4) Тело брошено вертикально вверх со скоростью, которая изменяется по закону 
Найдем время, в течении которого тело поднималось вверх: 29,4–9,8t=0 (в момент наибольшего подъема скорость равна нулю); t = 3 с. Поэтому
5) Какую работу совершает сила в 10Н при растяжении пружины на 2 см?
По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины , т.е. F = kx. Используя условие, находим 
6) Сила в 60Н растягивает пружину на 2 см. Первоначальная длина пружины равна 14 см. Какую работу нужно совершить, чтобы растянуть ее до 20 см?
Имеем 
7) Определить силу давления воды на стенку шлюза, длина которого 20 м, а высота 5 м (считая шлюз доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, 

8) В воду опущена прямоугольная пластинка, расположенная вертикально. Ее горизонтальная сторона равна 1 м, вертикальная 2 м. Верхняя сторона находится на глубине 0,5 м. Определить силу давления воды на пластинку.
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), 

9) Скорость прямолинейного движения точки задана уравнением 
Известно, что скорость прямолинейного движения тела равна производной пути s по времени t, т.е. 
Это искомое уравнение.
10) Скорость тела задана уравнением 


Имеем ds = v dt = (6
Подставив в найденное уравнение начальные условия s = 60 м, t = 3 c, получим

Искомое уравнение примет вид
11) Тело движется со скоростью 
Так как ds = v dt = (
Из условия следует, что если t = 0, то s = 5 см = 0,05 м. подставив эти данные в полученное уравнение, имеем 
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину, имеющую форму трапеции, у которой верхнее основание, совпадающее с поверхностью воды, имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
13) Цилиндрический стакан наполнен ртутью. Вычислить силу давления ртути на боковую поверхность стакана, если его высота 0,1 м, а радиус основания 0,04 м. Плотность ртути равна 13600 кг/
Вычислим площадь круглой полоски
Элементарная сила давления составляет
VI. Самостоятельное решение задач на доске, коллективный разбор решений задач:
- Скорость движения тела задана уравнением
. Найти уравнение движения, если в начальный момент времени
- Найти уравнение движения точки, если к моменту начала отсчета она прошла путь
, а его скорость задана уравнением
- Скорость движения тела пропорциональна квадрату времени. Найти уравнение движения тела, если известно, что за 3 с оно прошло 18 м.
- Тело движется прямолинейно со скоростью
м/с. Найти путь, пройденный телом за 5 с от начала движения.
- Скорость движения тела изменяется по закону
м/с. Найти путь, пройденный телом за 4 с от начала движения.
- Найти путь пройденный телом за 10-ю секунду, зная, что что скорость его прямолинейного движения выражается формулой
м/с.
- Найти путь, пройденный точкой от начала движения до ее остановки, если скорость ее прямолинейного движения изменяется по закону
м/с.
- Какую работу совершает сила в 8 Н при растяжении пружины на 6 см?
- Сила в 40 Н растягивает пружину на 0,04 м. Какую работу надо совершить, чтобы растянуть пружину на 0,02 м?
- Вычислить силу давления воды на вертикальную прямоугольную пластинку, основание которой 30 м, а высота 10 м, причем верхний конец пластинки совпадает с уровнем воды.
- Вычислить силу давления воды на одну из стенок аквариума, имеющего длину 30 см и высоту 20 см.
VII. Минутка релаксации
VIII. Подведение итогов урока:
– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее сложными? Почему?
Список литературы:
- Журнал «Потенциал»
- «Алгебра и начала анализа» 11 класс С.М. Никольский, М.К. Потапов и др.
- «Алгебра и математический анализ» Н.Я. Виленкин и др.
- «Учебник по математическому анализу» Град О.Г., Змеев О.А.
- «Высшая математика: Учебник для вузов». В 3 томах. Бугров Я.С. Никольский С.М.
- «Математический анализ». Е.Б. Боронина
Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
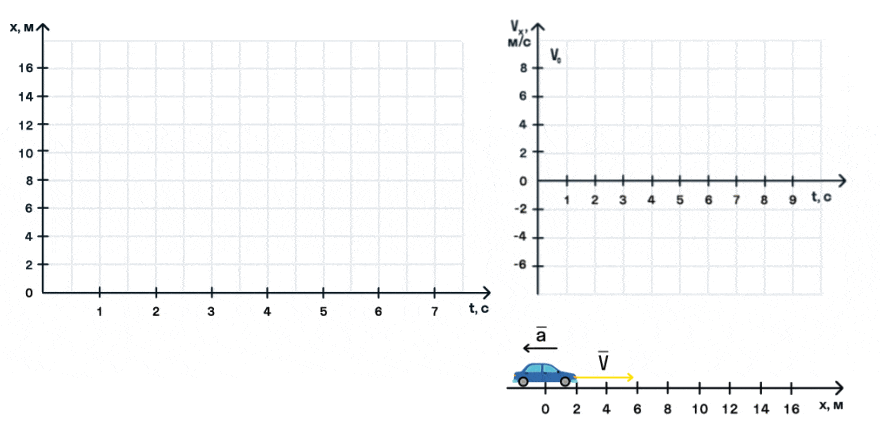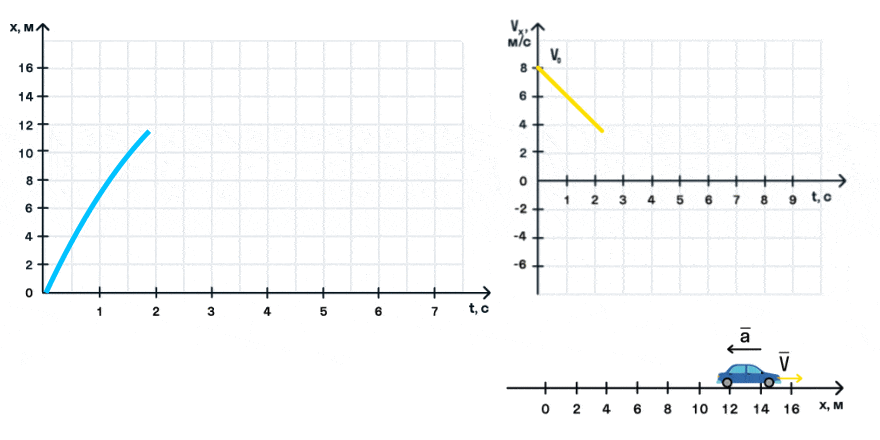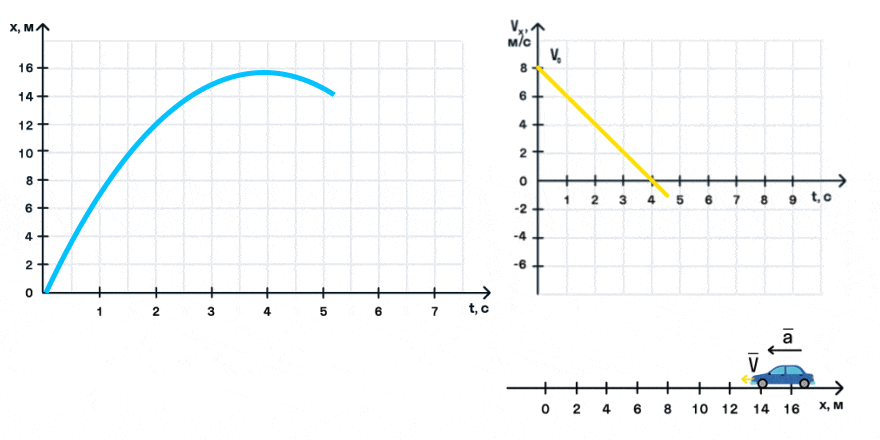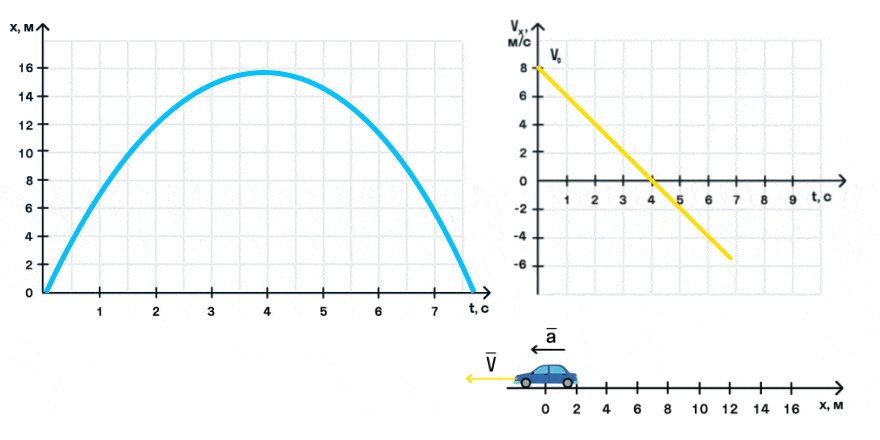
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

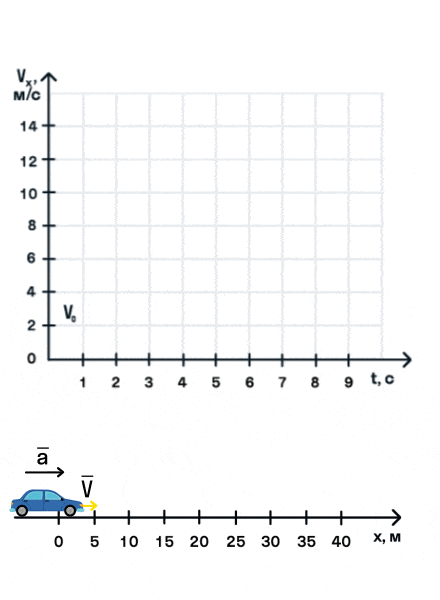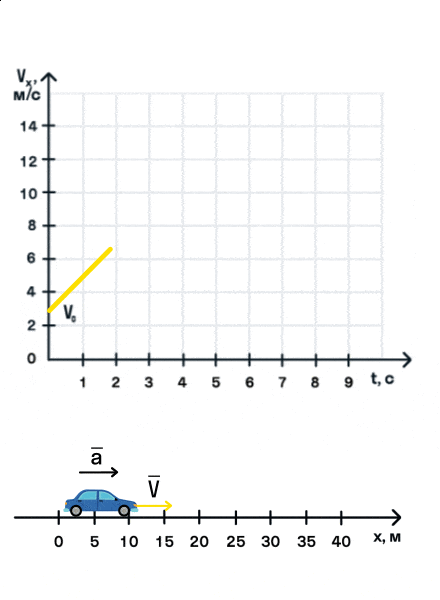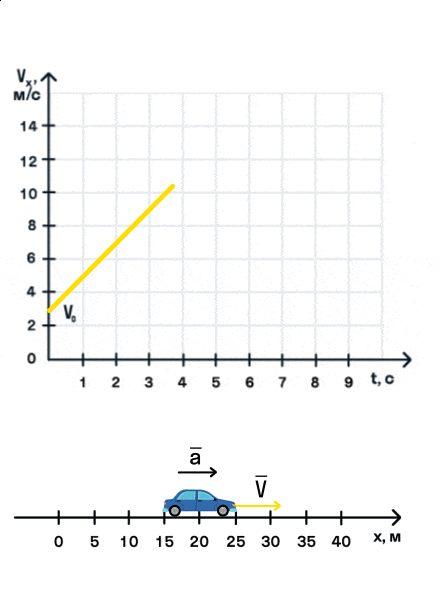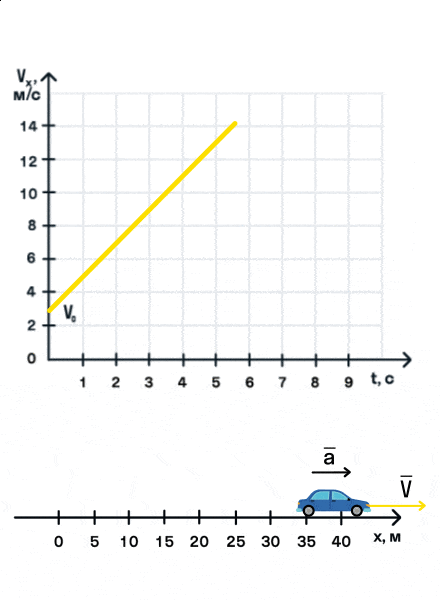
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
📸 Видео
Задачи на движение двух объектовСкачать

Физика 7 класс (Урок№8 - Скорость.)Скачать

Задача на среднюю скоростьСкачать

Равномерное прямолинейное движение - физика 9Скачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Графики зависимости пути и скорости от времениСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Физика 8 класс (Урок№28 - Скорость при неравном. движ. Ускорение и скорость при равноперем. движ.)Скачать

ЕГЭ по физике. Задание 1. Определение пройденного пути по графику скоростиСкачать
Упражнения на Верх Грудных - от Худших до КосмическихСкачать

Урок 19 (осн). Задачи на график движенияСкачать
Урок 25. График скорости РУД. Перемещение при РУД.Скачать


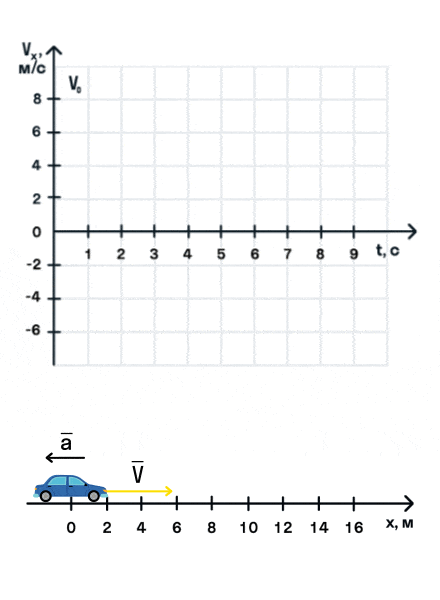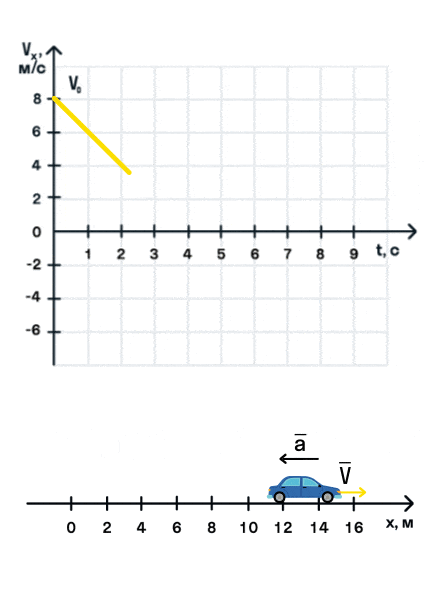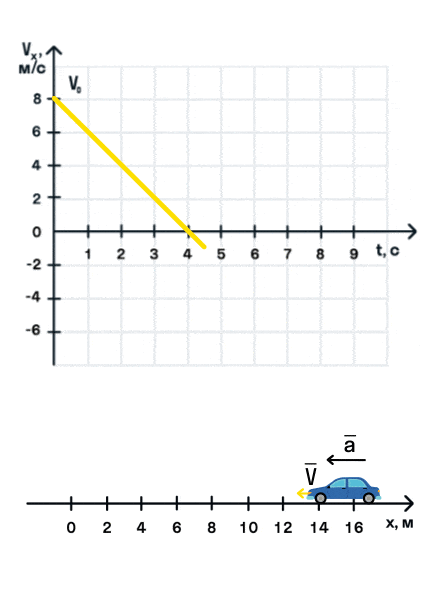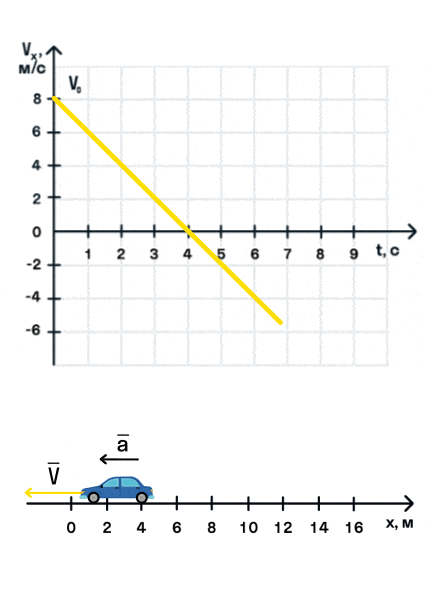










 , где
, где  – плотность жидкости.
– плотность жидкости.






















 . Найти уравнение движения, если в начальный момент времени
. Найти уравнение движения, если в начальный момент времени 
 , а его скорость задана уравнением
, а его скорость задана уравнением 
 м/с. Найти путь, пройденный телом за 5 с от начала движения.
м/с. Найти путь, пройденный телом за 5 с от начала движения. м/с. Найти путь, пройденный телом за 4 с от начала движения.
м/с. Найти путь, пройденный телом за 4 с от начала движения. м/с.
м/с. м/с.
м/с.






























