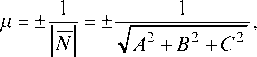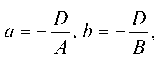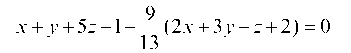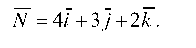Длина перпендикуляра опущенного из начала координат на прямую заданную уравнением 3х 4у 10 0 равна (6 видео)

Длина перпендикуляра опущенного из начала координат на прямую заданную уравнением 3х 4у 10 0 равна

Найти длину перпендикуляра, опущенного из начала координат на прямую 3x — 6y + 5 = 0, а также координаты основания этого перпендикуляра.

Приведем данное уравнение к нормальному виду:

После умножения на нормирующий множитель уравнение примет вид

Из сравнения с заключаем, что .

Для определения координат основания этого перпендикуляра из рисунка

(эти формулы верны при любом расположении прямой относительно координатных осей).

как видно из уравнения и искомые координаты основания перпендикуляра равны

Содержание

1.3.2. Аналитическая геометрия в пространстве
Онлайн калькулятор. Расстояние от точки до прямой на плоскости
Найти расстояние от точки до прямой на плоскости
Ввод данных в калькулятор для вычисления расстояния от точки до прямой на плоскости
Дополнительные возможности калькулятора для вычисления расстояния от точки до прямой на плоскости
Теория: Расстояние от точки до прямой на плоскости
Задача 26741 .
Условие
Решение
🌟 Видео

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

1.3.2. Аналитическая геометрия в пространстве

1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь

r = xi + yj + zk — радиус-вектор текущей точки плоскости

M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.

При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g — p = 0 (нормальное уравнение плоскости).

2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора

N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель

где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.

3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:

А = 0; плоскость параллельна оси ОХ;

В = 0; плоскость параллельна оси О^

C = 0; плоскость параллельна оси ОZ;

D = 0; плоскость проходит через начало координат;

А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);

А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);

В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);

А = D = 0; плоскость проходит через ось ОХ;

В = D = 0; плоскость проходит через ось OY;

C = D = 0; плоскость проходит через ось OZ;

А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);

А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);

B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).

Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на — D, можно уравнение

плоскости привести к виду^ здесь

. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.

4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле

Условие параллельности плоскостей:

Условие перпендикулярности плоскостей:

5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнениемНаходится по формуле

Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.

6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)

и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х — х0) + B(y — у0) + C(z — z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.

7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями

некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.

8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r — T1, r2 — rl, r3 — rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:

или в координатной форме:

Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z — 1 = 0, 2x + 3у — z + 2 = 0 и через точку М(3, 2, 1).

Решение. Воспользуемся уравнением пучка плоскостей

Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:

Получаем искомое уравнение в виде:

или, умножая на 13 и приводя подобные члены, в виде:

Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z — 4 = 0 и X — у — 2z + 7 = 0 и параллельной оси оу.

Решение. Воспользуемся уравнением пучка x + 3у + 5z — 4 + + l(x — у — 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 — 2l)z + (71 — 4) = 0.

Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 — l = 0, I = 3. Подставив значение I в уравнение пучка, получаем

Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z — 3 = 0.

Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:

Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:

Исключая коэффициенты А, В и C из системы уравнений

получаем искомое уравнение в виде:

Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.

Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением

Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору

Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:

1. Прямая может быть задана уравнениями 2-х плоскостей

пересекающихся по этой прямой.

2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.

3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:

4. Так называемые канонические уравнения

определяют прямую, проходящую через точку M(x1, у1, z1)

и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:

где a, b и g — углы, образованные прямой с осями координат.

5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:

6. Угол между двумя прямыми, заданными их каноническими

деляется по формуле

перпендикулярности двух прямых:

условие параллельности двух прямых:

7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):

Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.

условие параллельности прямой и плоскости: условие перпендикулярности прямой и плоскости:

Определяется по формуле

9. Для определения точки пересечения прямой

С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:

а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;

б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;

в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.

Пример 1.26. Привести к каноническому виду уравнения прямой 2х — у + 3z — 1 = 0 и 5х + 4у — z — 7 = 0.

Решение. Исключив вначале у, а затем z, получим:

Если разрешим каждое из уравнений относительно х, то будем иметь:

отсюда

Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i — j + 3k и N2= 5i + 4 j — k, то за него можно принять векторное произведение векторов N1 и N2.

Таким образом, l = -11; m = 17; n = 13.

За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:

Решая эту систему, находим у1 = 2; z1 = 1.

Итак, искомая прямая определяется уравнениями:

Мы получили прежний ответ.

Пример 1.27. Построить прямую

Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:

Пример 1.28. Из начала координат опустить перпендикуляр на прямую

Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).

Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:

Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).

Для определения t имеем уравнение:

Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):

Пример 1.29. В уравнениях прямойОпределить

параметр n так, чтобы эта прямая пересекалась с прямой

, и найти точку их пересечения.

Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:

Следовательно, уравнения пересекающихся прямых таковы: искомой:

Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенствоИмеем,

отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).

Пример 1.30. Прямая задана каноническими уравнениями

Составить общие уравнения этой прямой.

Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:

Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х — 3у — 13 = 0 параллельна оси Oz, а другая х + 3z — 11 = 0 параллельна оси Oy.

Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой

заключенный между плоскостями хoz и xoy.

Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:

отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).

отсюда X = 11, у = 14, или В(11; 14; 0).

Определяем координаты точки М, делящей отрезок АВ пополам:

Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).

Пример 1.32. Составить уравнение плоскости, проходящей через прямую

Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

которое делим на а ф 0, и пусть b /а = I:

Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:

В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:

Подставляя I = 1 в уравнение пучка плоскостей, получим: Тогда искомое уравнение плоскости будет:

Пример 1.33. Дана прямая Найти ее проекцию на плоскость

Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.

Составим уравнение пучка плоскостей, проходящих через данную прямую:

Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:

Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:

Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:

Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:

Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.

Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам

N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.

В качестве S берем векторное произведение векторов N1 и N2 , т. е.

Тогда искомое уравнение в каноническом виде будет:

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Онлайн калькулятор. Расстояние от точки до прямой на плоскости

Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до прямой.

Воспользовавшись онлайн калькулятором, вы получите детальное пощаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до прямой на плоскости и закрепить пройденный материал.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Найти расстояние от точки до прямой на плоскости

Ввод данных в калькулятор для вычисления расстояния от точки до прямой на плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления расстояния от точки до прямой на плоскости

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория: Расстояние от точки до прямой на плоскости

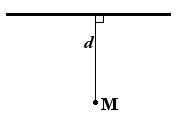
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если задано уравнение прямой на плоскости A x + B y + C = 0, то расстояние от точки M(M _x , M _y ) до прямой можно найти используя следующую формулу

d =	\|A·M _x + B·M _y + C\|
	√ A 2 + B 2

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Задача 26741 .

Условие

4.2.25. Составить уравнение прямой, зная, что расстояние от нее до
начала координат равно sqrt(2), а угол между перпендикуляром, опущенным из начала координат на прямую, и осью Ох, равен (3/4)Pi

Решение

Общее уравнение прямой у=kx+b
k- угловой коэффициент
k=tg альфа
альфа — угол, который прямая образует с положительным направлением оси Ох
Уравнение прямой образующей угол 3Pi/4 c положительным направлением оси Ох имеет вид
у=-х
k=tg (3Pi/4)=-1
k=0 — прямая проходит через начало координат

Перпендикулярная ей прямая — это прямая
у=х+d
Прямая у=х+d отсекает на осях координат отрезки длины d
Высота прямоугольного треугольника с катетами d и гипотенузой dsqrt(2) равна sqrt(2)
Значит,
из формул площади прямоугольного треугольника
S=(1/2)a*b
и
S=(1/2)c*h
получим
a*b=c*h
d*d=dsqrt(2)*sqrt(2)
d^2-2d=0
d=2