Вычисление длины дуги
Формула для вычисления длины дуги кривой заданной уравнением у=f(x) в прямоугольной системе координат:
a — начала дуги по оси OX;
b — конец дуги по оси OX a
Если плоская кривая задана уравнением x=g(y) то формула имеет вид:
c — начала дуги по оси OY;
d — конец дуги по оси OY a
Если кривая задана в полярных координатах r=r(φ), α≤φ≤β, то длина дуги вычисляется по формуле:
Если кривая задана параметрическим уравнением вида x=x(t) и y=y(t), то длина дуги определяется по формуле
t2 , t1 — значения параметров, которые соответствуют концам дуги t1
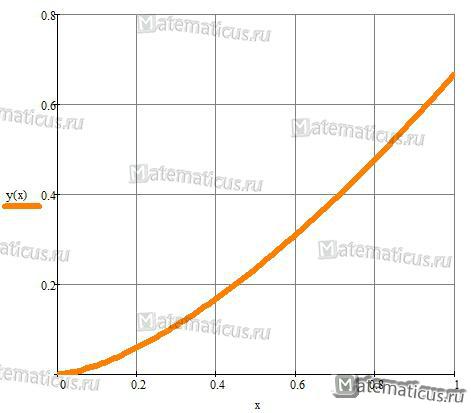
Найти длину дуги функции на промежутке от 0 до 1.
Найдем производную функции:
Возведём в квадрат функцию:
Подставляя в формулу, найдем длину дуги:
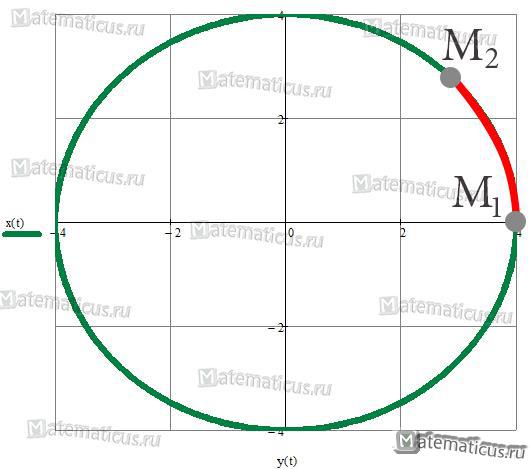
Найти длину дуги окружности от точки $left( right)$ до точки $left( right)$. Уравнение окружности задано в параметрическом виде.
Найдем параметр t в точках M1 и M2 , решим системы уравнений.
Здесь t1 =0
Подставляя в формулу, найдем длину дуги окружности.
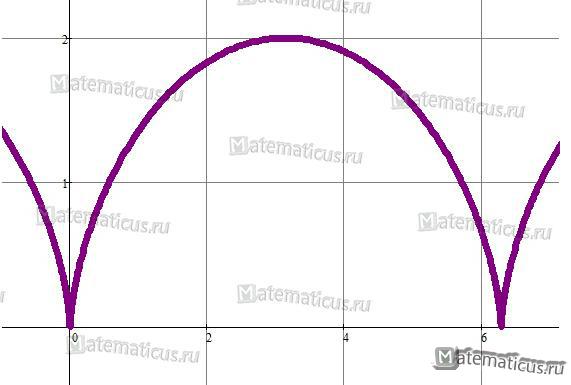
Вычислить длину дуги одного лепестка циклоиды. Уравнение циклоиды задано параметрическим уравнением.
Продифференцируем по t параметрические уравнения циклоиды:
Подставляя в формулу, получаем
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 4
Оценок пока нет. Поставьте оценку первым.
Видео: 14. Что такое параметрически заданная функция, производная параметрически заданной функции. Скачать
Была бы оценка 5, если бы не дурак, который не от большого ума изукрасил весь текст, особенно формулы и ответы, серыми узорами! Сколько времени и усилий ушло на расшифровку ответов! Так что 3,5 балла — это ещё слишком много! Так и передайте идеологу этой мазни!
Видео: Нахождение длины дуги кривой Скачать
Длина дуги плоской кривой заданной параметрически уравнениями Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты Администратор, решение задач Роман
Tel. +380685083397 [email protected] roman.yukhym
Решение задач Андрей
facebook: dniprovets25
Длина дуги плоской кривой заданной параметрически уравнениями         Пусть кривая задана уравнениями в параметрической форме
        Прежде, чем Вы начнёте скачивать свои варианты, попробуйте найти интеграл по образцу, приведённому ниже для варианта 27.
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        Задача 18.27. Вычислить длину дуги кривой, заданной параметрическими уравнениями.
Решение
        Найдём производные         Длина дуги кривой, заданной параметрически, ищется по формуле
        Подставляя данные, получим
        Ответ:    
🔥 Видео Видеоурок "Длина дуги кривой" Скачать
Вычисление длины дуги кривой в параметрических и полярных координатах. Вычисление объема тела. Скачать
Длина дуги кривой| Урок 1| Надежда Павловна Медведева Скачать
Кривые, заданные параметрически Скачать
Нахождение длины дуги кривой. Скачать
Видеоурок "Канонические уравнения прямой" Скачать
Как построить кривую, заданную параметрически Скачать
Матан за час. Шпаргалка для первокурсника. Высшая математика Скачать
Кривизна кривой, заданной параметрически Скачать
Длина кривой, заданной параметрически. Кривая в полярных координатах. Дифференциал дуги. 9 лекция Скачать
Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры. Скачать
Видеоурок "Параметрические уравнения прямой" Скачать
Длина эллипса и разложение в ряд для эллиптического интеграла Скачать
Астроида: найдем площадь и длину через определенный интеграл Скачать
Математика Без Ху!ни. Производная функции, заданной параметрически. Скачать
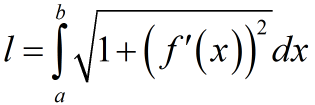
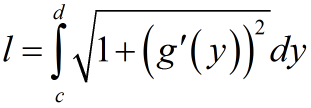
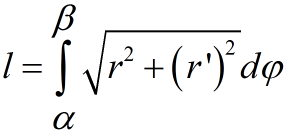
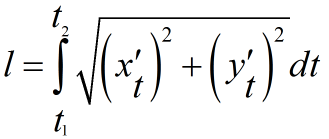
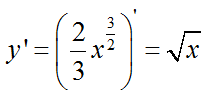
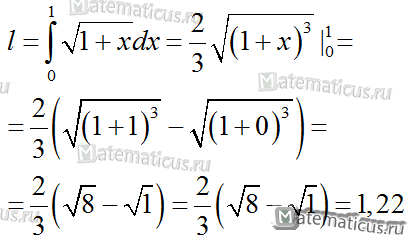
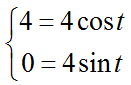
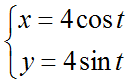
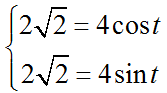
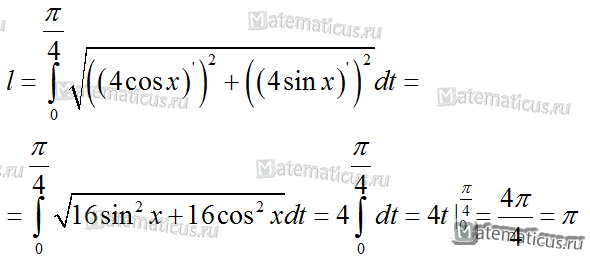
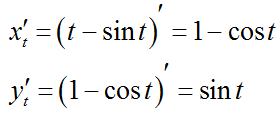
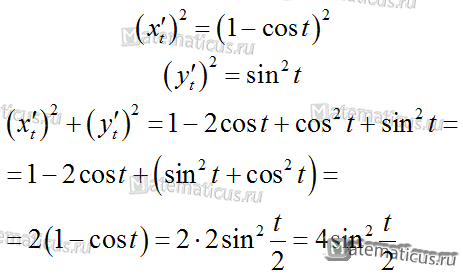
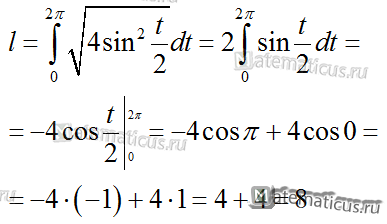
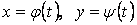
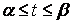    и     
    . 
    .
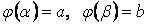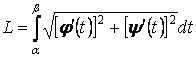
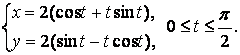
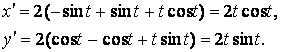
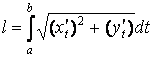
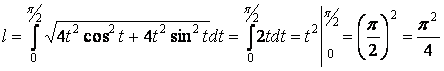
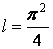