Динамическое уравнение движения груза на нити (3 видео)

Динамическое уравнение движения груза на нити

В эксперименте исследуется вращательное движение закрепленной на оси системы тел, у которой может меняться момент инерции. Различные моменты внешних сил создается грузами, подвешенными на нити, намотанной на шкив.

Основное уравнение вращательного движения твердого тела с моментом инерции J вокруг неподвижной оси z имеет вид (1.1)где — угловое ускорение, M — момент внешних сил.
Для экспериментального доказательства этого соотношения в работе используется маятник Обербека (рис.3). Он состоит из четырех стержней A и двух шкивов различного радиуса R₁ и R₂, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре (по одному на каждом стержне) груза одинаковой массы m ‘ . При помощи груза массы m, прикрепленного к концу намотанной на тот или иной шкив нити, маятник может приводиться во вращение.
Пренебрегая силами трения и считая нить невесомой и нерастяжимой, можем написать: уравнение вращательного движения маятника (1.2)уравнение поступательного движения груза на нити (1.3)уравнение кинематической связи (1.4)Здесь R — радиус шкива, T — натяжение нити, a — линейное ускорение груза массы m, g — ускорение свободного падения.
Из системы уравнений (1.2-1.4) следует, что груз m должен двигаться с постоянным ускорением (1.5)Основное уравнение вращательного движения (1.1) было записано без учета момента сил трения в оси маятника и момента сил вязкого трения о воздух. Для доказательства правомерности такого подхода в процессе выполнения работы необходимо убедиться , что суммарный момент сил трения M_тр много меньше момента силы натяжения нити M , который равен: С учетом неравенства mR 2 J можно записать, что M 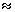mgR.
Оценить величину момента сил трения можно, если предположить, что он остается неизменным во время движения. При опускании груза m c отметки x₀ на полную длину нити до отметки x₃ и затем при последующем подъеме до отметки x₄ изменение его потенциальной энергии будет равно работе силы трения, то есть где Ф — полный угол поворота маятника Обербека. Причем поэтому Таким образом, условие малости момента сил трения окончательно имеет вид (1.6)

Установка для изучения вращательного движения (рис.4) или AVI (15.3M) состоит из основания (1), вертикальной колонны (2) с закрепленными на ней двумя подвижными кронштейнами (3,4), на которых крепятся оптические датчики положения. На колонне закреплены два неподвижных кронштейна (5,6).
На нижнем кронштейне (5) закреплен двухступенчатый вал (7). На верхнем кронштейне (6) закреплен подшипниковый узел (8) и блок (9). Через блок перекинута нить (10), один конец которой намотан на двухступенчатый вал (7), а на втором конце закреплен груз (11). На двухступенчатом валу крепятся тело маятника (12).
Кронштейны с фотодатчиками могут крепиться на разной высоте. Расстояние между этими кронштейнами измеряется по шкале, нанесенной на колонне. Время движения грузов определяют с помощью электронного таймера. Запуск таймера осуществляется нажатием кнопки «Пуск», остановка — кнопкой «Стоп». При подготовке к дальнейшим измерениям результаты предыдущих измерений убираются с табло таймера нажатием кнопки «Сброс».

Упражнение 1. Проверка закона движения.

Из (1.2-1.4) следует, что вращение маятника Обербека происходит с постоянным угловым ускорением 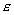, при этом груз m опускается с постоянным линейным ускорением a. Координата x груза, отпушенного без начальной скорости с отметки x₀ меняется по закону (ось х системы координат направлена вниз (см. рис. 3)) (1.7)Используя (1.7), определим время t пролета груза между двумя отметками x₁ и x₂: (1.8)Из (1.8) следует, что в случае равнопеременного движения (a=const) и фиксированных положений x₀ и, x₂ зависимость времени t от является линиейной и изображается на графике прямой линией.

Установить максимальное расстояние между кронштейнами с фотодатчиками
Установить грузы m ‘ в среднее положение, разместив их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия. Начало движения груза m всегда осуществляют от одного и того же положения x₀, которое необходимо записать в рабочий журнал. Нить наматывают на вал большего диаметра виток к витку.
Опустить груз m и произвести измерение времени t пролета груза m между фотодатчиками. Данные записать в таблицу 1.1 Провести измерения времени t для нескольких положений x₁ верхнего датчика (рекомендуется менять x₁ с шагом 5 см). Для каждого положения датчика измерения времени проводят не менее 3-х раз.
Для 5-7 первых опытов измерить значения x₄ — отметки, до которой поднимается груз при вращении маятника в одну сторону. Результаты занести в табл. 1.1.
Определить значение x₃ — максимальной отметки, до которой опускается груз m при своем движении.

Таблица 1.1

N	x_1i	x₄	t_ij	S
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Обработка результатов

По экспериментальным данным для каждого положения фотодатчика x₁ рассчитать среднее значение величины t_i по формуле

Динамическое уравнение движения груза на нити

где N — число измерений при каждом фиксированном положении датчика.

Вычислить ошибку измерения (выборочное стандартное отклонение)

Результаты вычислений внести в табл. 1.1.

Построить зависимость t от , которая должна быть линиейной. Получившаяся линейная зависимость указывает на то, что движение тела является равнопеременным.
Найти среднее значение и оценить величину по формуле (1.6). Убедиться в малости момента сил трения по сравнению с начальным моментом силы натяжения нити.

Упражнение 2. Проверка независимости инерционных свойств маятника (момента инерции) от момента внешних сил.

В данном упражнении экспериментально показывается, что инерционные свойства маятника, а именно — момент инерции — не зависят от момента внешних сил.
Из уравнения (1.2) имеем (1.9)Из уравнений (1.5), (1.8) следует, что (1.10)В уравнение (1.10) входят величины, определяемые экспериментально.

Измерить штангенциркулем радиусы R₁ и R₂ шкивов, результаты, занести в рабочую тетрадь.
Устаноновить максимальное расстояние между кронштейнами с фотодатчиками. Занести в рабочий журнал координаты фотодатчиков x₁, x₂ и значение x₀.
Установить грузы m ‘ в среднее положение, разместив их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия.
На конец нити, намотанной на шкив радиуса R₁, прикрепить груз массы m₁ и измерить время прохождения груза между двумя фотодатчиками t. Одновременно измерить x₄— отметку, до которой поднимается груз. Измерение провести 3 раза. и результаты внести в табл.1.2.
Перебросить нить на другой шкив (радиуса R₂). и измерить время t и значение x₄ (3 раза). Результаты внести в табл. 1.2.
Провести аналогичные измерения (п.4-п.5), прикрепив к концу нити груз массы m₂. Результаты измерений занести в табл.1.2.

Таблица 1.2

Комбинации значений радиусов шкивов и масс при измерениях	N	t_ij	x₄	, S	J_i , S_{J_i}
R₁ , m₁	1
	2
	3
R₂ , m₁	4
	5
	6
R₁ , m₂	7
	8
	9
R₂ , m₂	10
	11
	12

Обработка результатов

По экспериментальным данным вычислить средние значения величин t и ошибки их измерений для четырех различных опытов. Результаты вычислений внесети в табл.1.2.
Вычислить значения моментов инерции J₁:J₄ по формуле (1.10).
Определить значение для каждого опыта.
Найти отношение аналогично тому, как это было сделано в упр.1. Результаты внести в табл. 1.2.
Произвести оценку погрешностей полученных результатов. В связи с тем, что экспериментальные значения J_i являются результатом косвенных измерений, то стандартное отклонение функции нескольких независимых переменных находится через ошибки прямых измерений по формуле для ошибки косвенных измерений.
Проанализировать полученный результат. Для этого отметить значения моментов инерции J₁:J₄ с учетом погрешностей на числовых осях (рис.5), выбирая J_i=S_{J_i}. Пересечение этих областей будет указывать на выполнение соотношения (1.9) , что свидетельствеут о независимости инерционных свойств маятника от момента внешних сил.

Упражнение 3. Проверка основного уравнения вращательного движения и теоремы Гюйгенса-Штейнера.

Пусть J₀ ‘ — суммарный момент инерции четырех грузов с массами M ‘ относительно осей, проходящих через их центры масс. При удалении центров грузов на расстояние l=l₁, от оси вращения (см. рис. 3), согласно теореме Гюйгенса — Штейнера , момент инерции будет равен J₁ ‘ (1.11)Если J₀ — момент инерции маятника без грузов, то полный момент инерции маятника будет равен (1.12)При удалении центров масс грузов на расстояние l₂ соответственно имеем (1.13)С учетом уравнений (1.2)-(1.4) и (1.10) зависимость квадрата времени пролета груза между двумя отметками x₁ и x₂ от расстояния центра грузов m ‘ от оси вращения l имеет вид (1.14)Если l₁>l₂ , то (1.15)Уравнения (1.14)-и (1.15) дают (1.16)где t₁ , t₂ — времена пролета груза между датчиками для случаев l=l₁ и l=l₂ соответственно.
В это уравнение входят величины, определяемые экспериментально.

На конец нити, намотанной на шкив радиуса R₂ (большего по размеру), прикрепить груз наибольшей массы. Фотодатчики оставить в том же положении, что и в упражнении 2.
Установить минимальное значение момента инерции маятника. Для этого грузы m ‘ установить в положение, наиболее близкое к оси. Измерить расстояние от грузов до оси. Занести это значение в табл 1.3.
Определить величину t. — время прохождения груза m между двумя фотодатчиками и x₄ — отметку, до которой он поднимается в процессе движения.Измерения проводят 3 раза. Результаты заносят в табл.1.3.
Изменяя положение грузов m ‘ на стержнях с шагом 3 см, каждый раз измеряют время t. Результаты измерения и соответствующие им расстояния l от оси маятника до центров грузов записать в табл.1.3 . Одновременно для каждого опыта измеряют и заносят в табл. 1.3 значения величины x₄ .

Таблица 1.3

N	( #t_ij )	x₄	, S	( t_i ) 2 , S_{( t_i ) 2}	l	l 2
1
2
3
.

Обработка результатов

По экспериментальным данным для каждого положения грузов m ‘ найти средние значения величин t_i.
Вычислить погрешности измерения t_i и ( t_i) 2 .
Построить график зависимости квадрата времени опускания груза ( t_i) 2 . от l 2 , — это должна быть прямая линия.
Проверить соотношение (1.16) для нескольких пар значений t 2 и l 2 .
Для каждого момента инерции определить и отношение . Убедиться в выполнении приближения .

Основные итоги работы
В результате выполнения работы должна быть осуществлена экспериментальная проверка выполнения основного уравнения вращательного движения — уравнения моментов. Должны быть проверены соотношения (1.9) и (1.16) и установлена линейная ( t) 2 зависимость от l 2 .
Контрольные вопросы

Что такое абсолютно твердое тело? Сколько степеней свободы имеет твердое тело? Сколько независимых скалярных уравнений требуется для описания движения твердого тела?

Почему угловая скорость является вектором? Куда направлен этот вектор?

Что такое момент силы относительно некоторой точки? Куда он направлен? Что такое момент силы относительно закрепленной оси?

Что такое момент импульса системы тел?

Что такое момент инерции тела относительно закрепленной оси?

Сформулируйте теорему Гюйгенса-Штейнера.

Как получить уравнение моментов и основное уравнение вращательного движения относительно закрепленной оси?

Литература

Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, § 31,32,34.

Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд. M.: Наука.1989, § 30,35.

Видео:Физика.Решение задач.Выполнялка 1Скачать

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Цель работы – экспериментальная проверка основного уравнения динамики вращательного движения твердого тела вокруг закрепленной оси.

Идея эксперимента

В эксперименте исследуется вращательное движение закрепленной на оси системы тел, у которой может меняться момент инерции (маятник Обербека). Различные моменты внешних сил создаются грузами, подвешенными на нити, намотанной на шкив.

Теоретическая часть

Основное уравнение динамики вращательного движения твердого тела с моментом инерции J вокруг неподвижной оси z имеет вид

, (9.1)

где – угловое ускорение, М – полный момент внешних сил. Поскольку величина e является функцией двух переменных, то изучение закона динамики вращательного движения твердого тела выполняется путем раздельного исследования двух зависимостей:

Рис. 23. Маятник Обербека

1) зависимости углового ускорения от момента силы при постоянном значении момента инерции (J = const);

2) зависимости углового ускорения от момента инерции при постоянном значении момента силы (M = const).

Полный момент внешних сил равен

, (9.2)

где М_н – вращающий момент (в данной работе — момент силы натяжения нити), М_тр – момент силы трения. С учетом этого основное уравнение динамики вращательного движения принимает вид линейной зависимости момента силы натяжения М_н от e:

. (9.3)

Для экспериментального доказательства справедливости этого соотношения в работе используется маятник Обербека (рис. 23). Он состоит из четырех стержней А и двух шкивов с различными радиусами R₁ и R₂, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре цилиндрических груза (по одному на каждом стержне) одинаковой массы m₁. При помощи груза массы m, прикрепленного к концу нити, намотанной на тот или иной шкив, маятник может приводиться во вращение. Определяя продолжительность t движения и перемещение h груза, можно определить ускорение его поступательного движения

. (9.4)

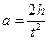
Это ускорение равно линейному ускорению точек шкива и связано с угловым ускорением крестовины соотношением

. (9.5)

Момент силы натяжения Т нити равен

. (9.6)

Силу Т можноопределить из второго закона Ньютона для поступательного движения, который в проекциях на ось 0Y дает

, (9.7)

Рис. 24. Зависимость момента силы натяжения нити от углового ускорения.

где m – масса груза.

Таким образом, момент сил натяжения нити равен

. (9.8)

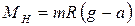
Согласно (9.3) М_н линейная функция e. На рис. 24 эти зависимости для различных значений моментов инерции системы изображены в виде графиков, угловые коэффициенты которых равны J. Эти графики отсекают от оси М_н отрезки, равные моменту силы трения М_тр. Так как М_тр одинаков во всех опытах, то все графики должны пересекаться в одной точке. Функция (9.3) верна для любых двух моментов сил, поэтому

(9.9)

. (9.10)

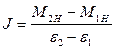
Таким образом, величина J может быть, с одной стороны, измерена, а с другой стороны, рассчитана, исходя из масс и геометрических размеров деталей установки Обербека. Момент инерции J маятника вычисляется из условия аддитивности момента инерции и равен сумме моментов инерции шкивов, крестовины и цилиндрических грузов, вращающихся вокруг оси, не проходящей через их середины. Графики позволяют также определить момент силы трения М_тр., действующей в системе.

Экспериментальная установка

Ось маятника Обербека закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции системы. На шкив виток к витку наматывается нить, к которой привязана платформа известной массы. На платформу накладываются грузы из набора. Высота падения грузов измеряется с помощью линейки, укрепленной параллельно нити. Маятник Обербека может быть снабжен электромагнитной муфтой – пускателем и электронным секундомером. Перед каждым опытом маятник следует тщательно отрегулировать. Особое внимание необходимо обратить на симметричность расположения грузов на крестовине. При этом маятник оказывается в состоянии безразличного равновесия.

Порядок выполнения работы

Задание 1. Оценка момента силы трения, действующей в системе.

1. Устанавливают грузы m₁ на крестовине в среднее положение, размещая их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия.

2. Накладывая небольшие грузы на платформу, определяют приближенно минимальную массу m₀, при которой маятник начнет вращаться. Оценивают момент силы трения из соотношения

, (9.11)

где R – радиус шкива, на который намотана нить.

3. Дальнейшие измерения желательно проводить с грузами массой .

Задание 2. Проверка основного уравнения динамики вращательного движения.

1. Укрепляют грузы m₁ на минимальном расстоянии от оси вращения. Балансируют маятник. Измеряют расстояние r от оси маятника до центров грузов.

2. Наматывают нить на один из шкивов. По масштабной линейке выбирают начальное положение платформы, производя отсчет, например, по ее нижнему краю. Тогда конечное положение груза будет находиться на уровне поднятой приемной платформы. Высота падения груза h равна разности этих отсчетов и может быть оставлена во всех опытах одинаковой.

3. Кладут на платформу первый груз. Расположив груз на уровне верхнего отсчета, фиксируют это положение, зажимая нить электромагнитной муфтой. Подготавливают к измерению электронный секундомер.

4. Отпускают нить, предоставив грузу возможность падать. Это достигается отключением муфты. При этом автоматически включается секундомер. Удар о приемную платформу останавливает падение груза и останавливает секундомер.

5. Измерение времени падения при одном и том же грузе выполняется не менее трех раз.

6. Проводят измерения времени падения груза m при других значениях момента М_н. Для этого либо добавляют на платформу дополнительные перегрузки, либо перебрасывают нить на другой шкив. При одном и том же значении момента инерции маятника необходимо провести измерения не менее чем с пятью значениями момента М_н.

7. Увеличивают момент инерции маятника. Для этого достаточно симметрично переместить грузы m₁ на несколько сантиметров. Шаг такого перемещения должен быть выбран таким образом, чтобы получить 5-6 значений момента инерции маятника. Проводят измерения времени падения груза m (п.2 – п.7). Все данные заносят в таблицу 1 отчета.

Обработка результатов. Исследование зависимости углового ускорения от момента силы при постоянном значении момента инерции.

1. Пользуясь формулами (9.4), (9.5), (9.8), определяют для каждого опыта по средним значениям времени значения линейного ускорения а, углового ускорения e и момента силы натяжения нити М_н.

2. Строят графики зависимостей момента силы М_н, как функции, от углового ускорения e, как аргумента, для различных моментов инерции маятника J. Т.к. М_н = f(e) – линейная функция, то ее графики будут прямыми линиями. Если экспериментальные точки не ложатся на прямую, графики надо проводить так, чтобы «разброс» точек был приблизительно одинаков по обе стороны прямой. При этом они не обязательно пройдут через одну точку на вертикальной оси. Малый «разброс» точек свидетельствует о хорошей линейности функции М_н = f(e) и том, что угловое ускорение действительно прямо пропорционально полному моменту сил, приложенных к вращающемуся телу.

Обработка результатов. Исследование зависимости углового ускорения от момента инерции при постоянном значении момента силы.

1. Для исследования используют ранее построенный график. Рассчитывают моменты инерции маятника по формуле (9.10). Для этого нужно выбирать точки прямо с графиков, например, А(М_1н,e₁)и В(М_2н,,e₂).

2. На графике проводят горизонтальную прямую через произвольную точку на оси М_н, пересекающую графики М_н = f(e). Точки пересечения позволяют определить те значения угловых ускорений маятника, которые соответствуют разным значениям моментов инерции, но при постоянном значении момента силы M = M_н – M_тр. Записывают полученные значения e и соответствующие им значения J в таблицу 2 отчета.

3. Угловое ускорение обратно пропорционально моменту инерции, т.е. график зависимости e = f(J) представляет собой гиперболу и не идентифицируется. Но график зависимости e = f(J -1 ) должен представлять собой прямую линию, проходящую через начало координат. Поэтому следует вычислить величины J -1 и построить соответствующий график. Угловой коэффициент наклона этого графика равен полному моменту приложенных сил.

Обработка результатов. Определение момента силы трения, действующей в системе.

1. В идеальном случае все графики M = f(e) должны пересекаться в одной точке, лежащей на оси М. Координата этой точки дает значение момента силы трения. Для реальных же графиков, скорее всего, будет иметь место некоторый разброс в положении этой точки.

2. Определить по графику все значения момента силы трения и найти его среднее значение. Сравнить полученный результат с ранее измеренным в задании 1.

Задание 3. Сравнение измеренных и вычисленных значений моментов инерции маятника.

1. Выписывают в таблицу 4 отчета измеренные значения моментов инерции маятника.

2. Используя формулы для расчета моментов инерции геометрически правильных тел и теорему Гюйгенса – Штейнера, вычисляют моменты инерции шкивов, крестовины и грузов, вращающихся вокруг оси, не проходящей через их середину. Данные для расчета берут из «паспорта» прибора. Общий момент инерции маятника находится суммированием моментов инерции деталей маятника.

3. Сравнивают вычисленные и измеренные значения моментов инерции. Находят относительные отклонения вычисленных и измеренных моментов инерции: .

Контрольные вопросы

1. Что называют моментом инерции материальной точки, твердого тела? Что называют моментом силы?

2. Запишите основное уравнение динамики вращательного движения.

3. Запишите кинематическое уравнение движения груза на нити.

4. Как связаны угловые и линейные кинематические величины?

5. Какая сила приводит во вращение маятник Обербека?

6. Запишите динамическое уравнение движения груза на нити.

7. Как рассчитать момент инерции маятника Обербека, используя данные эксперимента.

8. Сформулируйте теорему Гюйгенса-Штейнера.

9. Как рассчитать момент инерции маятника Обербека исходя из его геометрических размеров и формы?

Видео:Урок 315. Решение задач динамикиСкачать

Изучение динамики вращательного движения маховика

Лабораторная работа № 16

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ МАХОВИКА

Цель работы – экспериментальное определение момента инерции маховика, состоящего из диска, шкива и вала.

1. Теоретические основы работы

Аналогом второго закона Ньютона, справедливого для описания поступательного движения тела массой m

во вращательном движении является основное уравнение динамики вращательного движения

(2)

где и соответственно момент инерции и угловое ускорение твердого тела относительно неподвижной оси вращения z, – алгебраическая сумма моментов сил относительно оси z.

Сравнительный анализ уравнений (1) и (2) показывает, что роль массы в поступательном движении играет момент инерции тела во вращательном движении. А поскольку масса является мерой инертности тела в поступательном движении, то момент инерции является также мерой инертности тела во вращательном движении. В этом заключается физический смысл момента инерции.

Относительно неподвижной оси z момент инерции твердого тела определяется по формуле

, (3)

где r является кратчайшим расстоянием от элемента тела массой dm до оси z.

Из формулы (3) следует, что момент инерции зависит от массы тела и от ее распределения относительно оси вращения. Чем больше масса тела и чем дальше она находится от оси вращения, тем больше момент инерции твердого тела и наоборот.

Рассмотрим маховик (рис.1), состоящий из диска, шкива и вала. Предположим, что они обладают общей массой М. Диск и шкив насажены на общий вал, закрепленный в подшипниках. Маховик может вращаться относительно оси z, совпадающей с осью вала (на рис.1 ось z перпендикулярна плоскости чертежа и направлена «от нас»).

Рис.1 Схема системы маховик-груз (вал на схеме не показан)

Вращение маховика осуществляется под действием груза массой m1, укрепленного на нити, намотанной на шкив, и описывается относительно неподвижной оси z уравнением

, (4)

где момент инерции маховика, – его угловое ускорение, – сумма моментов сил, действующих на маховик. включает момент силы натяжения нити М(Т2) и момент силы трения М(Fтр) в подшипниках вала. Моменты сил N и Мg относительно оси z равны нулю. Таким образом

. (5)

Поступательное движение груза массой m1 описывается вторым законом Ньютона

, (6)

где а является ускорением центра масс груза, Т1 – силой натяжения нити, приложенной к грузу. В проекции на ось у уравнение (6) принимает вид

(7)

Так как предполагается, что нить нерастяжима и невесома, то ускорение всех точек нити и груза одинаковы, причем в отсутствии проскальзывания нити линейное (тангенциальное) ускорение обода диска равно ускорению груза. Силы натяжения нити Т1 и Т2 равны между собой (Т1 = Т2 = Т).

Предположим, что груз в процессе движения всей системы опускается до некоторого нулевого уровня с высоты h1. Тогда с учетом, что

, (8)

где t – время движения груза, а

; (9)

. (10)

Из уравнения (5) находим

. (11)

Силу натяжения Т выражаем из уравнения (7), а угловое ускорение e – из (10). Затем полученные формулы для Т и e подставляем в (11). В итоге получаем

. (12)

Для расчета нужно знать все величины, входящие в формулу (12). Они определяются экспериментально: – с помощью штангенциркуля, – с помощью линейки, t – с помощью секундомера. Масса груза m1 изначально задана. Момент силы трения определяется опытным путем. Для этого груз еще раз поднимают на первоначальную высоту (одновременно наматывая нить на шкив маховика), а затем предоставляют его самому себе. Груз сначала опускается на h1 до нижней точки – нулевого отсчета высоты (нить при этом сматывается со шкива), а затем (когда нить начинает наматываться на шкив) поднимается на меньшую высоту . Спуск и подъем груза происходят в течение некоторого времени t2 . Причиной подъема груза на меньшую высоту является наличие силы трения в подшипниках вала. Потеря механической энергии системы определяется работой силы трения

. (13)

Так как начальная и конечная кинетические энергии и равны нулю, то изменение механической энергии системы равно изменению только потенциальной энергии груза

. (14)

Работа силы трения выражается через момент силы трения и угловое перемещение маховика Dj :

. (15)

Приравнивая правые части уравнений (14) и (15), имеем

. (16)

Угловое перемещение маховика Dj равно отношению длины дуги, которую опишут за время поворота t2 точки обода шкива, к его радиусу:

Dj . (17)

Подставляя Dj в уравнение (16), имеем

. (18)

И, наконец, подставляя выражения для в уравнение (12), получаем формулу для определения экспериментального значения момента инерции маховика

. (19)

Экспериментально определенное значение Jzэ можно сравнить с теоретическим значением того же момента инерции Jzт, рассчитанного по формуле

Так как материал, из которого изготовлен шкив, обладает гораздо меньшей плотностью, чем плотность стальных диска и вала, то моментом инерции шкива Jz шкива можно пренебречь. Сам диск можно представить в виде совокупности двух элементов (см. раздел 2: «описание экспериментальной установки»).

, где

– момент инерции тонкого диска, – момент инерции кольца (здесь М1 и М2 являются соответственно массами тонкого диска и кольца, R1 – внешний радиус тонкого диска и одновременно внутренний радиус кольца, R2 – внешний радиус кольца).

. (20)

Данные установки представлены в разделе 2.

2. Описание экспериментальной установки

Схема экспериментальной установки приведена на рис.2. Основными ее элементами являются: диск 1, шкив 2 и груз 3. Груз подвешен на нити, намотанной на шкив. Диск вместе со шкивом смонтированы на едином соосным с ними валу 4. Вал крепится в подшипниках 5. Для регистрации местоположения груза в установке предусмотрена вертикально расположенная линейка 6. Все элементы установки смонтированы на массивной металлической опоре.

Рис. 2. Схема экспериментальной установки

Диск 1 представляет собой единую конструкцию в виде фигуры вращения. Диск для удобства расчета его момента инерции условно можно разделить на два отдельных элемента: тонкий диск (рис.3) и кольцо (рис.4):

Рис.3. Тонкий диск массой Рис.4. Кольцо массой

(Напоминаем, что моменты инерции этих тел не зависят от их толщины).

1. Заполните табл.1 спецификации измерительных приборов. Внесите в протокол данные установки.

Спецификация измерительных приборов

Название прибора и его тип

Масса груза m1 = Dm1 =

Момент инерции вала Jzвала = 1,36×10–4 кг×м2 DJzвала =

Масса тонкого диска = 2,91 кг D =

Радиус R1 = 162,0 мм DR1 = 0,25 мм

Масса кольца = 9,92 кг DМ2 =

Радиус R2 = 122,5 мм DR2 = 0,25 мм

2. С помощью штангенциркуля измерьте диаметр шкива d, значение диаметра запишите в табл.2. При построении таблицы предусмотрите необходимое для записи измерений число строк.

Измерение времени движения груза t, диаметр шкива d и высот h1 и h2

3. Проверьте, чтобы нижняя торцевая поверхность груза при полностью размотанной нити, к которой он подвешен, находилась на уровне нулевой отметки на шкале линейки (в противном случае за нулевую отметку примите то деление шкалы линейки, которое соответствует положению нижнего торца груза, когда нить полностью размотана).

4. Намотайте нить на шкив таким образом, чтобы нижняя торцевая поверхность груза располагалась напротив отметки на линейке, соответствующей высоте h1 (значение h1 согласуйте с преподавателем).

5. Предоставьте груз самому себе (отпустите), тем самым, заставив маховик вращаться; одновременно включите секундомер.

6. Выключите секундомер в момент достижения грузом нулевой отметки на шкале линейки. Полученное время движения груза t внесите в табл.2. Проделайте эксперимент по измерению диаметра шкива d (п.2) и по измерению времени t (п. п. 4,5,6) еще 4 раза. Всего измерений как d, так и t должно быть пять. Все измеренные значения d и t внесите в табл.2.

7. Поднимите груз на высоту h1 (одновременно наматывая нить на шкив) и вновь предоставьте его самому себе (отпустите). Наблюдая за поступательным движением груза, зафиксируйте максимальную высоту h2, на которую поднимется груз после прохождения им нулевой отметки на шкале линейки. Этот эксперимент повторите еще 4 раза. Значения h2 (всего 5 значений) внесите в табл.2.

4. Обработка результатов измерений

1. Рассчитайте значения радиуса шкива и внесите их в табл.2.

2. Используя данные, приведенные в табл.2, вычислите средние значения времени t, высот h1 и h2, радиуса r. Эти значения внесите в нижнюю строчку табл.2.

3. С учетом средних значений величин t, h1, h2 и r рассчитайте экспериментальное значение момента инерции маховика по формуле (19).

4. Рассчитайте теоретическое значение момента инерции маховика из уравнения (20). (Расчеты должны быть последовательными и должны включать буквенные обозначения величин и их численные значения. Это указание в полной мере относится и к расчетам погрешностей величин. Все расчеты должны быть выполнены в протоколе лабораторной работы).

5. Рассчитайте погрешность экспериментального значения момента инерции маховика по формуле: