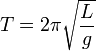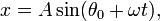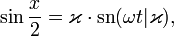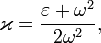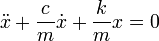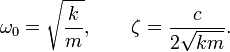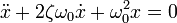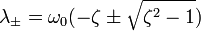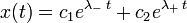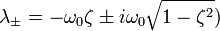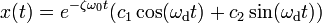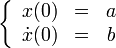Определение момента инерции тел методом колебаний
Физический маятник – это твёрдое тело, способное совершать колебания вокруг оси, лежащей выше его центра масс. Такое «устройство» оказывается весьма полезным. Так, с его помощью очень просто и с огромной степенью точности определяется ускорение силы тяжести. Также физический маятник позволяет определять моменты инерции различных твёрдых тел.
Малые колебание маятника вокруг оси – это его небольшие повороты в противоположные стороны, поэтому понять колебания физического маятника – это понять механику вращения. Механика вращения имеет тесную аналогию с механикой поступательного движения. Аналогия проявляется в основных понятиях механики, её идеях и закономерностях, и как следствие – в формулах и уравнениях, что удобно представить в виде «таблицы аналогий », которую следует твердо усвоить:
Поступательное движение Вращательное движение
| t время | t время |
| s путь | φ угловой путь (угол поворота тела вокруг оси) |
| v = ds/dt ≈ ∆s/∆t скорость (путь, пройденный за единицу времени | ω = dφ/dt ≈ ∆φ /∆t угловая скорость (угол поворота тела за единицу времени |
| a= dv/dt= d 2 s/dt 2 ускорение (изменение скорости тела за единицу времени) | ε = dω/dt= d 2 φ//dt 2 угловое ускорение (изменение угловой скорости за единицу времени) |
| F – сила (мера воздействия одного тела на другое; причина, изменяющая состояние движения) | M – момент силы (способность силы поворачивать тело; причина, изменяющая состояние вращения) |
| m – масса (мера инертности тела) | Iz — момент инерции (инертность тела при вращении) |
| p= mv – импульс ( запас движения) | L = Izω — вращательный импульс; он же – момент импульса ( запас вращения) |
Основной закон динамики (уравнение движения)
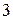 a=F/m a=F/m | ε =M/Iz |
(Рекомендуем студенту дополнить этот перечень аналогий для кинематики равномерного и равноускоренного движения, а также для работы, энергии и законов сохранения).
Мы видим, что в динамике вращения появились три новые величины с замысловатыми названиями: момент силы, момент инерции, момент импульса (он же угловой момент, он же вращательный импульс!). Да не болит голова у читателя по поводу таких названий; они появились в результате терминологических недоразумений прошлых веков с добавкой неадекватности перевода с иностранных языков; совершенно бесполезно вникать в смысл этих названий. Их надо просто запомнить. Для момента импульса это недоразумение достигает максимума – целых три названия. К счастью, одно из них оказалось порядочным – вращательный импульс, что просто отражает его аналогию соответствующей величине поступательного движения – обычному импульсу.
Дадим пояснения моменту силы M и моменту инерции Iz .
Момент силы. Возьмём твёрдое тело, закреплённое на оси. Приложим к нему в некоторой точке силу, и пусть линия действия силы пересекает ось вращения. Такая сила либо изогнёт ось вращения, либо вырвет ось из своего укрепления вместе с телом, ничего более.
Изменим немного опыт – сдвинем линию действия той же силы от оси на расстояние l . Эффект скажется незамедлительно: тело начнёт легко поворачиваться. Сила приобрела способность поворачивать тело. Эту способность силы поворачивать называют «моментом силы». Повседневный опыт говорит, что способность силы поворачивать тело зависит не только от силы, но и от «плеча силы» l (кратчайшего расстояния от линии действия силы до оси вращения). В итоге величина момента силы равна произведению силы на плечо:
Момент инерции относительно оси. Как уже было отмечено в «таблице аналогий», момент инерции (не обращать внимание на заумное название!) – величина, характеризующая инертность тела при вращении. Рассмотрим два совершенно одинаковых по форме и размерам волчка, но с заметно отличающими массами, скажем, алюминиевый и свинцовый. Мы легко обнаружим, что раскрутить до некоторой скорости (а так же потом остановить!) алюминиевый волчок гораздо легче, чем свинцовый. Значит, инертность тела при его вращении пропорциональна массе.
Далее, если бы у нас была возможность сильно расплющить любой волчок, отодвинув значительную часть его массы как можно дальше от оси вращения, превратив его в диск, то мы бы тот час обнаружили, что раскручивать (и останавливать) его стало заметно труднее, по сравнению с тем, когда он был компактным. Значит, инертность тела при вращении зависит не только от массы, но и от степени удаления её частей от оси вращения.
Момент инерции материальной точки массы m, находящейся на расстоянии r относительно оси z(рис.1), есть величина, равная произведению её массы на квадрат расстояния до оси вращения
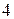
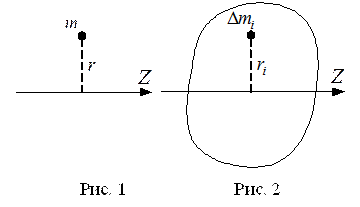
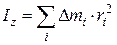

В пределе, когда Dmi строго превращаются в материальные точки, сумма(3)сводится к интегралу по объёму тела, и для тел простой (правильной) формы она точно вычисляется (таблицу моментов инерции тел правильной формы можно найти в справочниках и учебниках по общей физике). Отметим в заключение полезную формулу, известную как теорема Штейнера, позволяющую найти момент инерции тела относительно произвольной оси Z, если известен момент инерции тела Ic относительно оси, проходящей через центр инерции C (он же — центр масс, он же — центр тяжести) и параллельной данной оси:
здесь m – масса тела, a – расстояние между осями.
Теперь мы готовы к рассмотрению колебаний физического маятника (рис.3). Если отклонить его от положения равновесия на малый угол φ и предоставить самому себе, он начнёт совершать «малые» колебания. Для описания колебаний будем использовать один из основных способов решения физических задач – метод уравнения движения.
Уравнение движения в динамике вращения уже записано в «таблице аналогий»; оно отражает основной закон динамики вращения: если на тело действует внешняя сила, приводящая к возникновению момента силы, то тело вращается, причём его угловое ускорение пропорционально моменту силы и обратно пропорционально его моменту инерции:
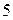
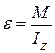
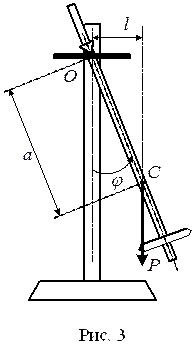
M = -Pl = — Pa sinφ = — mga sinφ ≈ — mgaφ (6)
Здесь учтено, что при малых отклонениях маятника синус угла можно заменить его аргументом (выраженным в радианах) sinφ ≈φ. Знак минус говорит о том, что при отклонении маятника на угол φ против часовой стрелки возникает момент силы тяжести, стремящийся повернуть маятник по часовой стрелке, т.е. возвратить его к положению равновесия.
В уравнении (5) искомая величина Iz. Остаётся расшифровать угловое ускорение. Угол отклонения φ (угловой путь!)зависит от времени, а угловое ускорение всегда есть вторая производная углового пути по времени (см. «таблицу аналогий»):
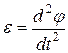
Подставляя (6) и (7) в (5), получаем уравнение движения малых колебаний физического маятника:
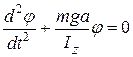
Из математики известно, что решение такого уравнения существенно зависит от знака коэффициента при φ . Величина mga/IZ заведомо положительна. Чтобы подчеркнуть это важное обстоятельство, mga/IZ записывают в виде квадрата некоторой действительной величины wo:
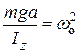
Теперь уравнение движения маятника принимает вид стандартного уравнения движения для гармонических колебаний
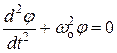
Решение этого уравнения представляет собой гармоническую функцию:
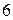
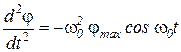
В гармоническом колебании (10) φmax – амплитуда колебаний, а woобретает точныйсмысл циклической частоты – числа колебаний за 2π секунд. (Учитывая, что за период колебания Т аргумент косинуса возрастает на 2π, имеем wo(t+T)=wot+2π, откуда wo =2π/T, т.е. именно число периодов за 2π секунд).
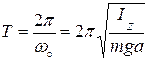
В итоге получаем формулу для экспериментального определения момента инерции физического маятника:
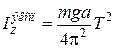
Видео:ЛР 1.05 Изучение колебаний физического маятникаСкачать

Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
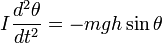
Полагая 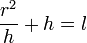
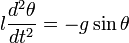
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
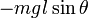
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
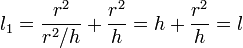
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 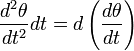
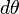
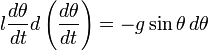
Интегрируя это уравнение, получаем.
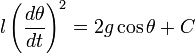
где 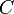
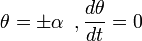
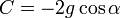
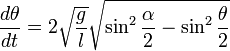
Отделяем переменные и интегрируем это уравнение:
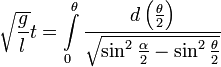
Удобно сделать замену переменной, полагая 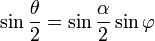
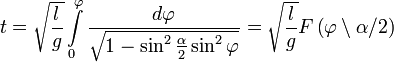
Здесь 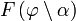
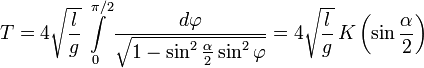
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 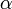
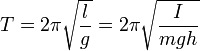
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 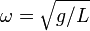
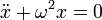
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 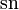

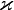
Параметр 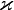
где 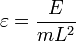
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
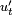
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
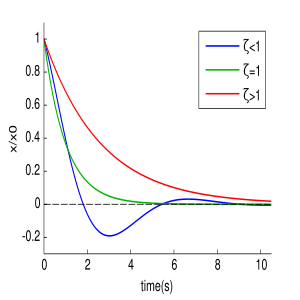
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 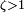
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 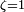
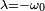
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 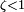
Тогда решением исходного дифференциального уравнения является
Где 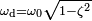
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 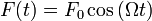
Видео:Математические и пружинные маятники. 11 класс.Скачать

Динамическое уравнение для физического маятника
«Физика — 11 класс»
Колебания тела можно описать, используя законы Ньютона.
Уравнение движения тела, колеблющегося под действием силы упругости.
Согласно второму закону Ньютона произведение массы тела на ускорение его равно равнодействующей всех сил, приложенных к телу:
Запишем уравнение движения для шарика, движущегося прямолинейно вдоль горизонтали под действием силы упругости Fупр пружины.
Направим ось ОХ вправо. Пусть начало отсчета координат соответствует положению равновесия шарика.
В проекции на ось ОХ уравнение движения можно записать так:
где ах и Fx упр — проекции ускорения и силы упругости пружины на эту ось.
Согласно закону Гука проекция Fx ynp прямо пропорциональна смещению шарика из положения равновесия.
Смещение же равно координате х шарика, причем проекция силы и координата имеют противоположные знаки. Следовательно,
Fx yпp = -kх
Разделив левую и правую части уравнения на массу, получим уравнение, описывающее колебания тела под действием силы упругости:
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.
Так как масса и жесткость пружины — постоянные величины, то их отношение также постоянная величина.
Уравнение движения математического маятника
При колебаниях маятника на нерастяжимой нити он все время движется по дуге окружности, радиус которой равен длине нити l.
Положение маятника в любой момент времени определяется одной величиной — углом альфа (α) отклонения нити от вертикали.
Пусть угол α>0, если маятник отклонен вправо от положения равновесия,
и α 0) составляющая силы тяжести Ft направлена влево и ее проекция отрицательна: Ft 0.
Проекция ускорения маятника на касательную к его траектории аt характеризует быстроту изменения модуля скорости маятника.
Поступая налогично выводу форулы для маятника, колеблющегося под действием силы упругости,
получим уравнение движения для математического маятника (нитяного маятника):
Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.
где
l — длина нити маятника,
g — ускорение свободного падения,
х — смещение маятника.
Вывод:
Движение маятника на пружине и колебания маятника на нити происходят одинаковым образом, хотя силы, вызывающие колебания, имеют различную физическую природу.
Ускорение прямо пропорционально координате (смещению от положения равновесия).
Колебания в этих двух случаях совершаются под действием сил, равнодействующая которых прямо пропорциональна смещению колеблющегося тела от положения равновесия и направлена в сторону, противоположную этому смещению.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Механические колебания. Физика, учебник для 11 класса — Класс!ная физика
🎥 Видео
9. Колебания физического маятникаСкачать

Колебания математического и пружинного маятников. 9 класс.Скачать

Физический маятникСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

физический маятникСкачать

Физический маятникСкачать

математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Механика. Л 10.2. Колебания. Вывод дифф уравнений колебаний математического и физического маятниковСкачать

Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

Почти всё о маятникеСкачать

УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ДЛЯ ФИЗИЧЕСКОГО МАЯТНИКАСкачать

Физический маятник.Скачать

Колебания. Физический маятник. Период и частота колебаний физического маятника.Скачать

Негармонические колебания физического маятникаСкачать

Математический маятник или откуда формула периодаСкачать

Лабораторная работа №2 - "Физический маятник"Скачать

Теормех. 2021-окт-18. Группа ПМФ. Двойной маятникСкачать

Урок 326. Динамика колебательного движенияСкачать

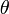 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;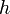 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.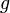 — ускорение свободного падения.
— ускорение свободного падения.