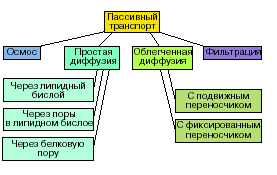
Законы Фика.
Прохождение многих незаряженных веществ через мембраны подчиняется законам диффузии.
Процесс диффузии был впервые количественно описан Фиком.
Первый закон Фика поток вещества J в направлении оси х пропорционален движущей силе (градиенту концентрации dc/dx)
где D — коэффициент диффузии, см^ 2 с^-1; размерность потока — моль • см^2с^-1
F — число Фарадея,
Z — валентность иона,
T — абсолютная температура,
R — газовая постоянная,
— электрический потенциал на мембране.
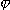
Из сопоставления и видно, что D = RTu, где R— газовая постоянная, Т — абсолютная температура, U — подвижность вещества в рассматриваемой среде. В случае стационарной диффузии через тонкие мембраны dc/dx = const. Если на краях мембраны толщиной h поддерживаются постоянные концентрации (с’1 и c’2), связанные с концентрациями в омывающих растворах (с1 и с2) соотношениями с’1 = гаммаc1 и с’2 = гамма с 2, где гамма — коэффициент распределения, то поток равен
Здесь p = Dгамма/h = uRTгамма/h— проницаемость мембраны для данного вещества, см * с^-1; коэффициент у отражает липофильность вещества; и — подвижность вещества в мембране.
В общем случае нестационарной диффузии концентрация вещества в любой точке по оси х изменяется во времени.
элементарный объем с площадью 5 = 1 см 2 и толщиной dx
в точке х поток J, a в точке (х + dx) поток J + (dJ/dx)dx,
dJ/dx — градиент потока в направлении оси х.
Количество вещества, накапливающегося в рассматриваемом объеме за единицу времени, равно —<dJ/dx)dx. Количество вещества, накапливающегося в элементарном объеме, можно выразить как результат изменения концентрации во времени dc/dt, умноженной на объем V = S dx. Приравнивая эти два разных выражения, описывающие накопление вещества в объеме, получаем так называемое уравнение непрерывности
Подставляя (1) в (2), получаем выражение для второго закона Фика:
дc/дt = Dд 2 c/дx 2 .
описывает изменение концентрации растворенного вещества в зависимости от координаты х и времени.
решение имеет вид C=c0/2(ПиDt)^0.5 exp(-x^2/4Dt) (3)
c0 — общее количество вещества, нанесенного в начальный момент времени
t = 0 в точке х = 0
с — концентрация в точке х в любой момент t
Профили концентрации вещества по координате х для двух различных моментов времени, описываемые уравнением (3), приведены на рис1
Для выпуклых участков кривой д 2 с/дх 2 2 c/дx 2 ., dc/dt 2 c/dx 2 > 0. Следовательно, dc/dt > 0, т. е. концентрация вещества в этих участках во времени повышается. Полученный результат отражает известный факт, что диффузия всегда направлена на выравнивание концентрационных градиентов.
.Профиль C, достигаемый к моменту времени t, хар пар-тром х с черточкой. C вещества на расстоянии х с черточкой уменьшается в е раз по сравнению с концентрацией в начальной точке, если показатель экспоненты в уравнении (3) равен единице: х с черточкой^2 /4Dt = 1.
Формула выше характеризует время, необходимое для диффузии, увеличивается пропорционально квадрату расстояния.
Связь проницаемости мембран с растворимостью проникающих веществ в липидах.
Коэффициент диффузии определяется размером и формой молекул. Для малых молекул в воде D
10 ^-5 см^2 • с^-1. Для сферических частиц уравнение Стокса—Эйнштейна, связывающее коэффициент диффузии с радиусом частиц г и вязкостью среды ню:
Малые гидрофильные молекулы могут проникать через поры в мембране
Для проникновения неэлектролитов из воды в гидрофобную часть мембраны или узкую мембранную пору необходима частичная или полная дегидратация молекул, затраты энергии на преодоление взаимодействий полярных групп молекулы (—СООН, —ОН, —NH2) с диполями воды. Например, значения энергии активации, полученные для проникновения этиленгликоля, глицерина и эритрита через искусственные фосфолипидные мембраны, а также через мембраны изолированных клеток, близки к значениям энергии дегидратации этих соединений. Необходимость дегидратации молекул является причиной сильной температурной зависимости коэффициента проницаемости мембран для ряда неэлектролитов. Хотя через биологические мембраны диффундируют самые разные соединения, в то же время даже сравнительно небольшие молекулы аминокислот и моносахаридов практически не проникают через мембраны большинства клеток за счет простой диффузии.
Дата добавления: 2016-04-11 ; просмотров: 1524 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 12 (осн). Диффузия. Броуновское движениеСкачать
Биофизика. Тест 2 по теме 11 Физич процессы в мембранах без ответов. Физические процессы в биологических мембранах
| Название | Физические процессы в биологических мембранах |
| Анкор | Биофизика |
| Дата | 14.05.2020 |
| Размер | 58.4 Kb. |
| Формат файла |  |
| Имя файла | Тест 2 по теме 11 Физич процессы в мембранах без ответов.docx |
| Тип | Документы #122801 |
| Подборка по базе: КР1 процессы,аппараты Кузнецов А.С. ЗМТО-101.docx, 1. Физика – наука о природе. Физические тела. Физические явления, Что мне дают физические упражнения.docx, Лекция 1 Физические эффекты, используемые для создания датчиков., Есть разные точки зрения на процессы.docx, Тепловые процессы.pdf, свойства биологических систем.docx, Инновационные процессы.docx, Контрольная работа по биологии на тему _Основные процессы жизнед, ЛАБА №6 ПРОЦЕССЫ УСТАНОВЛЕНИЯ ТОКА ПРИ РАЗРЯДКЕ И ЗАРЯДКЕ.docx ФИЗИЧЕСКИЕ ПРОЦЕССЫ В БИОЛОГИЧЕСКИХ МЕМБРАНАХ 1. Основу структуры биологических мембран составляют: г) аминокислоты; д) двойная спираль ДНК. 2. Диффузию незаряженных частиц через мембраны описывает уравнение: a) J = -D(dc/dx); б) Q = Δр/Х; в) F = η(dv/dx)S; 3. Для возникновения трансмембранной разности потенциалов необходимо и достаточно: а) наличие избирательной проницаемости мембраны; б) различие концентраций ионов по обе стороны от мембраны; в) наличие избирательной проницаемости и различие концентраций ионов по обе стороны от мембраны; г) появление автоволновых процессов; д) повышенная проницаемость для ионов. 4. Активный транспорт ионов осуществляется за счёт… а) энергии гидролиза макроэргических связей АТФ; б) процессов диффузии ионов через мембраны; в) переноса ионов через мембрану с участием молекул — переносчиков; г) латеральной диффузии молекул в мембране; д) электродиффузии ионов. 5. Латеральной диффузией молекул в мембранах называется . а) вращательное движение молекул; б) перескок молекул поперек мембраны — из одного монослоя в другой; в) перемещение молекул вдоль плоскости мембраны; г) активный транспорт молекул через мембрану; д) пассивный транспорт молекул через мембрану. 6. Вязкость липидного слоя мембран близка к вязкости: а) воды; б) этанола; в) ацетона; г) растительного масла. 7. Плотность потока вещества J имеет размерность: а) моль/(м 3 ·с); б) моль/(м 2 ∙с); в) моль/(м∙с); г) моль/с; д) моль/м. 8. Коэффициент проницаемости Р вещества через мембрану имеет размерность: а) м/с; б) с/м 2 ; в) моль/(м 2 ∙с); г) дм 3 /(моль∙см); д) кДж/м 2 . 9. Уравнение Нернста-Планка показывает, что . а) потенциал покоя возникает в результате активного транспорта; б) перенос ионов определяется неравномерностью их распределения (градиентом концентрации) и воздействием электрического поля (градиентом электрического потенциала); в) главная роль в возникновении потенциала покоя принадлежит ионам калия; г) мембраны обладают избирательной проницаемостью; д) коэффициент проницаемости веществ через мембрану определяется их подвижностью. 10. Коэффициентом распределения вещества называют… а) соотношение концентраций катионов внутри клетки и снаружи; б) равновесное соотношение концентраций исследуемого вещества в мембране и окружающей водной среде; в) соотношение концентраций исследуемого вещества в окружающей клетку водной среде и в цитоплазме; г) параметр, характеризующий скорость проникновения вещества через мембрану; д) соотношение концентраций катионов и анионов внутри биологических мембран. а) напряженность электрического поля в биологических мембранах; б) способность мембран к активному транспорту; в) вероятность возникновения каналов проницаемости в мембране; г) способность исследуемого вещества растворяться в биологических мембранах; д) соотношение скоростей переноса катионов и анионов через мембраны. 12. Укажите, при каких условиях пассивный перенос катионов через мембрану может происходить из раствора, где его концентрация ниже, в более концентрированный раствор: ? б) если вязкость мембраны низкая; в) при наличии в мембране интегральных белков; г) если мембрана обладает избирательной проницаемостью для катионов. 13. Пассивный перенос ионов описывается уравнением Нернста-Планка. Как модифицируется это уравнение, если ион превратится в незаряженную частицу? а) Уравнение Норнста-Планка превратится в уравнение Гольдмана-Ходжкина-Катца; б) Уравнение утратит смысл; в) Уравнение не изменится; г) Уравнение Нернста-Планка превратится в уравнение Фика. 14. При условии, что мембрана проницаема только для ионов калия, уравнение Гольдмана-Ходжкина-Катца трансформируется в уравнение… а) Нернста-Планка для ионов калия; б) Нернста для ионов калия; в) Фика для диффузии ионов калия. 15. Укажите, при каких условиях при решении дифференциального уравнения б) Если мембрана проницаема только для одного вида ионов и для этих ионов J=0; в) Если мембрана одинаково проницаема для катионов и анионов; г) Если градиент концентрации и градиент потенциала равны нулю. 1. 1) Структурной основой биологической мембраны являются белки. 2) Обязательным структурным компонентом биологических мембран являются соединения, состоящие из полярной «головки» и неполярного «хвоста», например, фосфолипиды. 3) Латеральная диффузия липидов и белков в биомембранах осуществляется значительно быстрое, чем диффузия поперёк мембраны — из слоя в слой. 4) Латеральная диффузия липидов и белков в биомембранах осуществляется значительно медленнее, чем диффузия поперек мембраны — из слоя в слой. 2. 1) Вязкость липидного бислоя биомембран близка к вязкости воды. 2) Вязкость липидного бислоя биомембран значительно выше вязкости воды и близка к вязкости растительного масла. 3) Вещество диффундирует через мембрану тем легче, чем выше его коэффициент распределения. 3. 1) Вещество диффундирует через мембрану тем легче, чем меньше его коэффициент распределения. 2) Облегчённая диффузия — это перенос ионов специальными молекулами — переносчиками. 3) Облегчённой называют диффузию веществ, имеющих высокие значения коэффициента распределения. 4. 1) Диффузия заряженных частиц через мембрану подчиняется уравнению Фика. 2) Диффузия заряженных частиц через мембрану подчиняется уравнению Нернста-Планка. 3) Диффузия незаряженных частиц через мембрану подчиняется уравнению Нернста-Планка. 5. 1) Коэффициент проницаемости мембраны для ионов калия выше, чем для ионов натрия или хлора, когда на мембране клетки генерируется потенциал покоя. 2) При возникновении потенциала действия коэффициент проницаемости мембраны для ионов натрия имеет самое высокое значение. 3) При возникновении потенциала действия коэффициент проницаемости мембраны для ионов хлора имеет самое высокое значение. 6. 1) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение только потенциала покоя, но не потенциала действия. 2) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение только потенциала действия, но не потенциала покоя. 3) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение трансмембранной разности потенциалов на мембранах как в случае генерации потенциалов покоя, так и потенциалов действия. 1. 1) Плотность потока вещества a) P=Dk/I ; 2) Коэффициент проницаемости , б) dc/dx ; 3) Градиент концентрации в) J= — D. 1) напряженностью поля и градиентом потенциала 2) потоком и плотностью потока вещества 3) плотностью потока и градиентом концентрации 2) Облегченная диффузия происходит б) через липидный слой; 3) Диффузия через канал происходит в) в комплексе с переносчиком. 2) Активный транспорт происходит б) без затраты энергии; 3) Облегченная диффузия ионов происходит в) при участии калий-натриевого насоса. 2) Диффузия ионов подчиняется б) уравнению Гольдмана-Ходжкина-Катца; 3) Диффузия незаряженных частиц подчиняется в) уравнению Нернста-Планка. 1) коэффициент проницаемости а) моль/(м 2 с); 2) плотность потока вещества б) В/м; 3) градиент потенциала в) м/с; 4) коэффициент диффузии г) безразмерная величина; 5) коэффициент распределения д) м 2 /с. 1. Коэффициент проницаемости мембран определяется выражением P=Dk/l, где D- коэффициент диффузии paccматриваемых частиц в… А. 1) омывающем мембрану растворе; 2) веществе самой мембраны; Б. k -… 1) коэффициент, характеризующий избирательную проницаемость мембраны; 2) Коэффициент распределения, характеризующий соотношение равновесных концентраций диффундирующего вещества в мембране и в окружающем растворе; 3) постоянная Больцмана; В. l -. 1) толщина мембраны; 2) размер диффундирующей через мембрану молекулы; 3) размер канала в мембране, по которому осуществляется диффузия. А. 1) Фика; 2) Нернста-Планка; 3) Эйнштейна; 4) Ньютона; Б. Диффузия вещества через мембрану осуществляется тем легче, чем . . . У) больше значение коэффициента проницаемости; 2) больше толщина мембраны; 3) меньше значение коэффициента распределения; Д. и тем трудное, чем . . . Трменьшс значение коэффициента распределения; 2) больше толщина мембраны; 3) больше значение коэффициента проницаемости. ГУ. . . транспорт вещества через мембрану т? Пассивный; 2) Активный; 1) в результате латеральной диффузии; 2) благодаря её емкостным свойствам; 3) без затраты энергии. 3. А. Для возникновения трансмембранной разности потенциалов необходимо и достаточно выполнения следующих двух условий. 1) мембрана должна содержать интегральные белки; 2) мембрана должна содержать поверхностные белки; |>)должна существовать избирательная проницаемость ионов через мембрану; ?) концентрации ионов по обе стороны от мембраны должны различаться; Б. При возникновении стационарного трансмембранного потенциала . . . Шшотность потока каждого иона равна нулю; ^^Х^уммарная плотность потока ионов равна нулю, но плотности потоков отдельных ионов не равны нулю; 3) плотность потока анионов равна нулю. В. Возникновение потенциала покоя обусловлено, главным образом, высокой избира-юпьной проницаемостью мембран для ионов . . . J/калия; 2) натрия; 3) хлора. Г. Возникновение потенциала действия обусловлено, главным образом, высокой избирательной проницаемостью для ионов . . . 1) калия; /йГЬатрия; 3) хлора. 4. А. Если мембрана ^дбладает . . . проницаемостью 1) одинаковой; 2) избирательной; 3)низкой; 1)воды; 2))эдного вида ионов; 3) незаряженных молекул; В. и их концонтра*1Д1Я по обе стороны мембраны 1) высокая; 2)7/разная; 3) одинаковая; Г. то на мембране 4 /. . . -1J,будет происходить латеральная диффузия белков; (^’возникнет разность электрических потенциалов; 3) прекратится латеральная диффузия фосфолипидов. 5 А. . . . транспорт ионов через мембраны >г$Уктивный; ^рЧассивный; Тэ. осуществляется за счет . . . 1) латеральной диффузии белков; 2) градиента их концентрации и градиента потенциала электрического поля; 3) явления «флип-флопа»|Г»у>химичоской энергии. В. Такие процессы описываются уравнением . . . 6. А. Трансмембранная разность . 1) осмотического давления; 2ЬЬлектрических потенциалов; 3) концентраций ионов; Нернста-Планка; 2) Фика; 3) Гольдмана-Ходжкина-Катца; и возникает в результате . . . переноса ионов. I) пассивною; 2) латерального; 3) активного. Г. Для её возникновения необходимо, чтобы мембрана обладала . . . проницаемостью для разных ионов неодинаковой; 2) одинаковой; 3) высокой; 4) низкой; Д. и чтобы концентрации ионов . по разные стороны мембраны. 1) не различались; 2) равнялись нулю; 3) различались. Задание 5. Решите задачу и укажите правильный ответ: 1. Пусть трансмембранная разность потенциалов составляет 58 мВ при 20°С. Чему она станет равна, если температуру увеличить до 35°С? 1) не изменится; 2) 61 мВ; 3) 116 мВ; 4) 29 мВ. 2. Пусть отношение концентраций ионов калия по разные стороны от мембраны равно 10 и мембрана избирательно проницаема для калия. Возникающая при этом трансмембранная разность потенциалов равна 60 мВ. Чему будет равна разность потенциалов, если заменить ионы калия ионами кальция в тех же концентрациях и сделать мембрану избирательно проницаемой для кальция? 1)120мВ; 2)60мВ; 3) 30 мВ; 4)0. 3. Потенциал покоя нерва конечности краба равен 89 мВ. Чему равна концентрация ионов калия внутри нерва, если снаружи она составляет 12 мМ? Принять температуру равной 20°С. Видео:Потенциал покоя и равновесный потенциалСкачать  Поток вещества, растворяемогов биомимбране. Уравнение Фика, проницаемостьПроницаемость биологических мембран имеет большое значение для осморегуляции и поддержания постоянства состава клетки, её физико-химический гомеостаз; играет важную роль в генерации и проведении нервного импульса, в энергообеспечении клетки, сенсорных механизмах и др. процессах жизнедеятельности. Проницаемость биологических мембран обусловлена особенностями строения БМ, являющихся осмотическим барьером между клеткой и средой, и служит характерным примером единства и взаимосвязи между структурой и функцией на молекулярном уровне. С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обусловливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала
В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае больших концентраций, так как химический потенциал перестаёт быть связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то вышеприведённую формулу можно заменить на следующую:
которая показывает, что плотность потока вещества J [
Коэффициент диффузии D зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой уравнение Аррениуса. Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера—Планка. Процессы диффузии имеют большое значение в природе: · Питание, дыхание животных и растений; · Проникновение кислорода из крови в ткани человека.
6.6 Диффузия электрическизаряженных частиц через мембрану. Электродиффузия — диффузия электрически заряженных частиц (ионов) под влиянием концентрационных и электрических градиентов. Ионы — атомы или группы атомов, которые приобретают электрический заряд, теряя или приобретая электроны. Липидный бислой мембраны непроницаем для ионов. Они могут проникнуть через плазматическую мембрану только посредством специальных структур — ионных каналов, которые образованы интегральными белками. Движущей силой диффузии является не только разность концентрации ионов внутри и вне клетки, но также разность электрических потенциалов, создаваемых этими ионами по обе стороны мембраны. Следовательно, диффузионный поток ионов определяется градиентом электрохимического потенциала (электрохимический градиент). Электрохимический потенциал является энергией ионов:
μ0— стандартный химический потенциал, который зависит от химической природы вещества и температуры, R — универсальная газовая постоянная, T — температура, C — концентрация иона, z — электрический заряд, F — константа Фарадея, φ — электрический потенциал. Зависимость потока ионов J от электрохимического градиента определяется уравнением Теорелла:
где U — подвижность ионов, C — концентрация ионов, dμ/dx — электрохимический градиент. Подставляя (6) в (7), можно получить уравнение Нернста-Планка с учётом двух градиентов, которые обуславливают диффузию ионов:
Ионные каналы мембраны представляют собой интегральные белки мембраны, которые образуют отверстия в мембране, заполненные водой. В плазматической мембране обнаружен ряд ионных каналов, которые характеризуются высокой специфичностью, допускающей перемещение только одного вида ионов. Существуют натриевые, калиевые, кальциевые и хлорные каналы. Каждый из них имеет так называемый селективный фильтр, который способен пропускать только определённые ионы. Существует несколько теорий, объясняющих избирательность ионных каналов плазматической мембраны. Проницаемость ионных каналов может изменяться благодаря наличию ворот, определенных групп атомов в составе белков, формирующих канал. Конформационные изменения ворот переводят канал из открытого состояния в закрытое и наоборот. Механизмы регуляции положения ворот могут отличаться в различных каналах. Некоторые из них открываются при изменениях электрического потенциала мембраны. Другие открываются под действием специфических химических веществ, выполняющих сигнальные функции. Электрохимический градиент Электрохимический градиент (DmX, уравнение 2–3). Пассивный транспортзаряженного растворённого вещества Х зависит как от разности концентраций вещества в клетке ([X]В) и вне (снаружи) клетки ([X]С), так и от разницы электрического потенциала вне (YС) и внутри клетки (YВ). Другими словами, DmX учитывает вклад как концентрационного градиента вещества (разность химического потенциала), так и вклад электрического потенциала по обе стороны мембраны (разность электрического потенциала).
где: zХ — валентность вещества X, Таким образом, движущей силой пассивного транспорта электролитовявляется электрохимический градиент — разность электрохимического потенциала (DmX) по обе стороны биологической мембраны. 6.7. (1)Поток вещества через мембрану при наличии осмотического и электрического градиентов. Уравнение Нернста – Планка. На мембране существует разность потенциалов, следовательно в мембране имеется электрическое поле. Оно оказывает влияние на диффузию заряженных частиц (ионов и электронов). Между напряженностью поля и градиентом потенциала существует известное соотношение
В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т.е. градиентом концентрации и взаимодействием электрического поля
— уравнение Нернста – Планка. F — число Фарадея, Z — валентность иона, T — абсолютная температура, R — газовая постоянная,
Этоуравнениеописываетпроцесспассивноготранспортаионоввполеэлектрохимическогопотенциала и используется для установления зависимости плотности диффузного потока от концентрации ионов и от напряжения электрического поля. Поток вещества через мембрану при наличии осматического и электрического градиентов. Уравнение Нериста-Планка О́смос (от греч. ὄσμος — толчок, давление) — процесс односторонней диффузии через полупроницаемую мембрану молекул растворителя в сторону бо́льшей концентрации растворённого вещества (меньшей концентрации растворителя). Осмос играет важную роль во многих биологических процессах. Мембрана, окружающая нормальную клетку крови, проницаема лишь для молекул воды, кислорода, некоторых из растворённых в крови питательных веществ и продуктов клеточной жизнедеятельности; для больших белковых молекул, находящихся в растворённом состоянии внутри клетки, она непроницаема. Поэтому белки, столь важные для биологических процессов, остаются внутри клетки. Осмос участвует в переносе питательных веществ в стволах высоких деревьев, где капиллярный перенос не способен выполнить эту функцию. Осмос широко используют в лабораторной технике: при определении молярных характеристик полимеров, концентрировании растворов, исследовании разнообразных биологических структур. Осмотические явления иногда используются в промышленности, например при получении некоторых полимерных материалов, очистке высоко-минерализованной воды методом обратного осмоса жидкостей. Клетки растений используют осмос также для увеличения объёма вакуоли, чтобы она распирала стенки клетки (тургорное давление). Клетки растений делают это путём запасания сахарозы. Увеличивая или уменьшая концентрацию сахарозы в цитоплазме, клетки могут регулировать осмос. За счёт этого повышается упругость растения в целом. С изменениями тургорного давления связаны многие движения растений (например, движения усов гороха и других лазающих растений). Пресноводные простейшие также имеют вакуоль, но задача вакуолей простейших заключается лишь в откачивании лишней воды из цитоплазмы для поддержания постоянной концентрации растворённых в ней веществ. Осмос также играет большую роль в экологии водоёмов. Если концентрация соли и других веществ в воде поднимется или упадёт, то обитатели этих вод погибнут из-за пагубного воздействия осмоса. Нернста закон распределения определяет относительное содержание в двух несмешивающихся или ограниченно смешивающихся жидкостях растворимого в них компонента; является одним из законов идеальных разбавленных растворов. Открыт в 1890 В. Нернстом.Согласно Н. з. р., при равновесии отношение концентраций третьего компонента в двух жидких фазах является постоянной величиной. Н. з. р. может быть записан в виде c1/c2=k, где c1 и c2 — равновесные молярные концентрации третьего компонента в первой и второй фазах; постоянная k — коэффициент распределения, зависящий от температуры. Н. з. р. позволяет определить более выгодные условия экстрагирования веществ из растворов 6.8.Пассивный транспорт вещества через мембраны. Виды пассивного транспорта.
Пассивный транспорт – это перенос вещества из мест с большим значением электрохимического потенциала к местам с его меньшим значением. Пассивный транспорт идет с уменьшением энергии Гиббса и поэтому этот процесс может идти самопроизвольно и без затраты энергии Пассивный транспорт не зависит от энергии, обеспечиваемой АТФ. В его основе лежит разность концентраций и зарядов и он всегда стремится выровнять концентрации частиц по разные стороны от мембраны, то есть свести к нулю их градиенты. Виды пассивного транспорта: 1) Транспорт веществ через липидный бислой (простая диффузия) 2) Транспорт веществ через мембранные каналы 3) Транспорт веществ через специальные транспортные белки (облегченная диффузия) Простая диффузия происходит без участия мембранного белка за счет тепловыхпрцессов- тепловой и физической дифузи, непосредственно через липидный бислой. Через него легко проходят газы, неполярные или малые незаряженные полярные молекулы. Диффузию воды через мембраны называют осмосом. Вода, очень быстро проникает через липидныйбислой. Это объясняется тем, что ее молекула мала и электрически нейтральна. Диффузия через мембранные каналы. Заряженные молекулы и ионы (Na+, K+, Ca2+, Cl-) не способны проходить через липидный бислой путем простой диффузии, тем не менее, они проникают через мембрану, благодаря наличию в ней особых белков, формирующих различные каналы. Облегченная диффузия — транспорт веществ с помощью специальных транспортных белков, каждый из которых отвечает за транспорт определенных молекул 🎦 ВидеоЗакон диффузии ФикаСкачать  Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать  Броуновское движение. Диффузия в жидкостях, газах и твердых телах | Физика 7 класс #5 | ИнфоурокСкачать  Осмос. Диффузия. Броуновское движение. Нефелометрия и турбодиметрия | Лекция 4 | Коллоидная химияСкачать  10.1 Закон Фика и уравнение диффузии моноэнергетических нейтронов (часть 1)Скачать  Матрица интенсивностей. Система уравнений КолмогороваСкачать  ЭТОТ метод поможет на уроках ХИМИИ / Химия 9 классСкачать  Многомерный анализ, интегралы и ряды 27. Дифференциальное исчисление в ЛНПСкачать  Обработка результатов эксперимента. 5. Погрешность косвенных измеренийСкачать  Дифференциальные уравнения, Ремизов А. О., лекция 1, 01.09.2023Скачать  ✓ Система неравенств с параметром | ЕГЭ-2017. Задание 17. Математика. Профиль | Борис ТрушинСкачать  Механика - Теория упругости (продолжение). Гидродинамика идеальной жидкостиСкачать  Стехиометрические расчеты. Практическая часть - решение задачи. 9 класс.Скачать  Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать  Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать  |
(уравнения Нернста-Планка) получается уравнение
(уравнение Нернста)?
] пропорциональна коэффициенту диффузии D [( 
)] и градиенту концентрации. Это уравнение выражает первый закон Фика. Второй закон Фика связывает пространственное и временное изменения концентрации (уравнение диффузии):
— электрический потенциал на мембране.
