Распределение концентраций в пограничном слое. Стационарная диффузия в условиях естественной и вынужденной конвекции. Вращающийся дисковый электрод и его применение. Вращающийся цилиндрический электрод и другие системы с известным распределением концентраций в пограничном слое.
Ранее было показано, что электрохимическая ячейка или электрохимическая цепь может работать либо как электролизёр, либо как источник тока.
В первом случае электрическая энергия, поступающая от внешнего источника тока, затрачивается на проведение каких — либо электрохимических реакций. Благодаря ним могут осуществляться электрохимическая размерная обработка металлов, электроосаждение слоёв на поверхности какого — либо изделия, электрохимический синтез каких — либо материалов, электролитическое получение газов (водорода, кислорода, хлора и других).
Во втором случае происходит использование электрохимических реакций с целью получения электрического тока, т.е. электрохимические реакции, происходящие на границе электрод – электролит могут использоваться как генераторы электроэнергии (батареи, аккумуляторы, топливные элементы).
Под током общее напряжение ячейки всегда отличается от напряжения в отсутствие тока, т.е.:
(10.1)
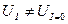
В первом случае, т.е. когда электрохимическая ячейка работает как электролизёр:
(10.2)
Во втором случае (ячейка является источником тока):
(10.3)
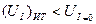
То есть реализуемая мощность источника тока всегда меньше его теоретической мощности:
(10.4)
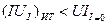
Для случая, когда система работает как электролизёр, можно записать:
(10.5)
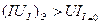
Таким образом, всегда есть дополнительное падение напряжения, необходимое для того, чтобы можно было осуществить реакцию с конечной скоростью. И это дополнительное падение напряжения тем больше, чем больше величина плотности тока на электроде, и связана она, как ясно из вышеприведённого, с перенапряжением.
Первый вид перенапряжения, которое будет рассмотрено, это — перенапряжение, обусловленное разницей концентраций на поверхности электрода и в объёме раствора. Разница концентраций всегда приводит к наличию переноса массы (массопереноса).
Существуют три механизма массопереноса:
- молекулярная диффузия; движущая сила этого процесса – разница (градиент) концентрации;
- миграция (перенос в электрическом поле);
- Конвекция (перенос частиц в связи с движением раствора, его перемешиванием); в условиях отсутствия перемешивания перенос осуществляется посредством естественной конвекции, обусловленной градиентом плотности раствора.
В случае наличия градиента концентрации возникает поток диффузии jD, обусловленный разницей концентрации:
(первый закон Фика) (10.6)
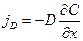
Подставляя в уравнение для закона Фарадея это соотношение, покажем, что в том случае, когда скорость электрохимической реакции определяется диффузией (т.е. лимитирующей стадией суммарного электрохимического процесса является диффузия), мы можем написать:
(10.7)
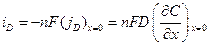
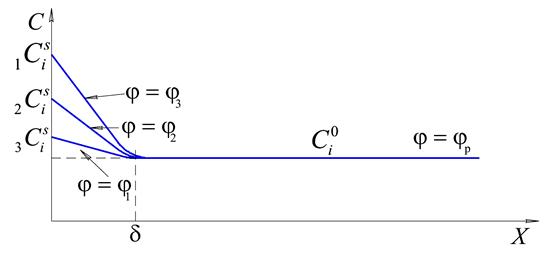
Уравнение (10.7) — основное уравнение диффузионной кинетики, т.е. такого электрохимического процесса, который определяется скоростью диффузии. При этом все его стадии предполагаются равновесными, а неравновесной является только диффузионная стадия. В этом случае должен существовать некоторый слой толщиной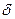 
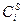
, в котором будет наблюдаться разность концентраций (см. рис. 10.1). Поверхностная концентрация 
будет изменяться при изменении потенциала, потому что будет увеличиваться скорость окисления (восстановления) при росте потенциала.
Рис. 10.1 Распределение концентрации у поверхности электрода,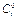 
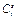
-объёмная концентрация компонента электролита, который восстанавливается или окисляется на поверхности электрода. 
-поверхностная концентрация того же компонента, зависящего от приложенного потенциала
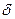
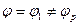
Для этой концентрации по уравнению Нернста может быть рассчитан равновесный потенциал. В отсутствие тока никаких изменений концентрации происходить не будет. При появлении тока в процессе электроосаждения непосредственно на поверхности концентрация снизится, потому что часть ионов перейдёт в металлическую фазу. Область, в которой будет наблюдаться это изменение, обозначается буквой и носит название диффузионного пограничного слоя. Этот процесс будет происходить при 
.
1. всегда будет существовать некий слой, величиной 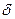,который называется диффузионным пограничным слоем, внутри которого концентрация будет отличаться от объёмной;
2. градиент концентрации будет тем выше, чем в большей степени потенциал будет отличаться от равновесного или, чем большую плотность тока мы будем пропускать через ячейку;
3. должно существовать предельное состояние, при котором, как видно из рис. 10.1, поверхностная концентрация (концентрация на поверхности 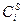) станет равной нулю.
Понятие о диффузионном слое впервые было введено В.Нернстом. Учитывая вышеизложенное и уравнение (10.7), можно записать:
(10.8)
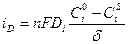
или в предельном случае при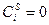 
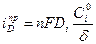
, получим:
(10.9)
Из уравнения (10.8) и (10.9) следует, что величина диффузионного тока (плотности тока) обратно пропорциональна толщине диффузионного слоя. В общем случае толщина диффузионного слоя зависит от температуры и вязкости раствора, от скорости его перемешивания и от координаты на поверхности электрода, т.е. его толщина может быть различной для разных точек поверхности электрода.
В том случае, если происходит анодное растворение металла, поверхностная концентрация будет более высокой, чем объёмная концентрация, поскольку ионы не будут успевать отводиться от поверхности (рис. 10.2).
|
Рис. 10.2 Распределение концентраций в диффузионном слое при растворении электрода (увеличение поверхностной концентрации при увеличении потенциала).
Согласно уравнению (10.9) предельное значение плотности тока связано с установлением на поверхности таких условий, когда достигается предельное значение поверхностной концентрации ионов. При электроосаждении это нулевая концентрация. При анодном растворении это очень часто концентрация насыщения, определяемая достижением произведения растворимости.
Видео:Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать
Кинетика диффузионно-контролируемых химических реакций
Кинетика диффузионно-контролируемых химических реакций
1. Основные понятия кинетики диффузионно-контролируемых химических реакций
Феноменологическое описание методов и проблем диффузионной кинетики довольно широко и полно обсуждено в ряде отечественных и зарубежных монографий 5. В этих работах основное внимание уделено формулировке уравнений переноса в рамках онзагеровской термодинамики и методам решения уравнений диффузионной кинетики.
Большинство проводимых в настоящее время исследований реакций в жидких растворах основано на предположении о применимости к описанию диффузии молекул в растворе макроскопических законов диффузии Фика. Диффузия молекулы в растворе, рассматриваемая как процесс хаотических блужданий, после большого числа блужданий описывается законами Фика, если в уравнении Фика заменить концентрацию функцией плотности вероятности. Экспериментально обнаружено, что законы Фика становятся применимыми уже по прошествии 10
13 с после того, как молекула начала диффундировать. Это позволяет заключить, что уравнения диффузии, выведенные из законов Фика, являются хорошим приближением для описания кинетики диффузионных процессов.
Теория кинетики реакций, контролируемых диффузией, была впервые сформулирована Смолуховским. Ее основная идея заключается в том, что скорость реакции может определяться медленным диффузионным движением, необходимым для сближения партнеров по реакции, после чего реакция протекает почти мгновенно. Из многих применений этой теории упомянем рост коллоидных или аэрозольных частиц, осаждение, катализ и тушение флуоресценции. Она была также применена к исследованию горения, в котором роль диффундирующих частиц играет окислитель, распространяющийся в среде – капле горючего. Теория Смолуховского была усовершенствована Дебаем, который дополнительно ввел в нее учет возможных взаимодействий. Наиболее общая математическая формулировка этой теории дана Вилемским и Фиксманом [7], которые применили ее для описания цепных реакций в полимерах [8].
2. Диффузия. Законы Фика
Диффузией называется процесс переноса вещества, обусловленный самопроизвольным выравниванием его концентрации в первоначально неоднородной системе. В результате процесса диффузии устанавливается одинаковый химический потенциал каждого компонента во всех элементах объема системы. Если в пределах всей системы температура одинакова, то диффузия приводит к самопроизвольному выравниванию концентраций. В тех случаях, когда в системе имеется температурный или какой-либо другой градиент, влияющий на значение химического потенциала вещества, диффузия может привести даже к еще большему увеличению разности концентраций.
Процессы диффузии описываются законами Фика. Первый закон Фика, который описывает стационарную диффузию, устанавливает связь между количеством вещества 
, продиффундировавшего за время 
через площадь S, пропорционально градиенту концентрации :
. (1.1)
В более общем виде диффузия характеризуется потоком Ji, равным массе вещества, проходящей за единицу времени через условную единичную поверхность, располагаемую перпендикулярно направлению потока:
, (1.2)
где – масса i вещества, переносимая за время через поверхность, площадь которой равна S; Di – коэффициентом диффузии. Знак минус перед указывает на то, что процесс диффузии идет в направлении уменьшения концентрации.
Второй закон Фика описывает изменение общей концентрации диффундирующего вещества в каждой точке среды:
, (1.3)
где 
– оператор Лапласа; 
–функция, описывающая рождение или гибель диффундирующих молекул в каждой точке среды.
В декартовых координатах оператор Лапласа имеет вид:
. (1.4)
В цилиндрических координатах:
. (1.5)
В сферических координатах:
. (1.6)
Выражение (4) фактически является уравнением материального баланса
Для диффузии в одном направлении (одномерная диффузия) второй закон Фика записывается в следующем виде:
. (1.7)
Отметим, что величина наблюдаемого потока зависит не только от процесса диффузии, но и от действия на частицы внешних сил. Если внешняя сила Fх, направленная вдоль оси х, сообщает частице скорость wx, то возникает дополнительная составляющая потока, равная ci ∙wx. С ее учетом поток вещества определяется уравнением:
. (1.8)
В этом же случае вместо уравнения, выражающего второй закон Фика, применяется уравнение Фоккера-Планка:
. (1.9)
Коэффициент диффузии является константой скорости диффузионного процесса. Он численно равен количеству вещества (в молях), проходящему через единицу площади (1 см2) за единицу времени (1 с) при градиенте концентрации, равном единице (т. е. изменению концентрации в 1 моль/см3 на расстоянии в 1 см). Размерность коэффициента диффузии:
или 
. (1.10)
Величина коэффициента диффузии чаще всего оценивается из экспериментальных данных, однако его можно оценить из ряда известных соотношений.
Коэффициент диффузии молекул в газовой фазе равен:
, (1.11)
где 
, 
, 
– средние величины длинны свободного пробега, скорости и времени между столкновениями.
Коэффициент диффузии для кристалла, в котором диффундирующее вещество скачками перемещается по узлам правильной решетки, можно оценить по соотношению:
, (1.12)
где 
– параметр решетки, 
– частота диффузионных скачков.
Для оценки коэффициента диффузии сферических частиц в растворах, размеры которых гораздо больше, чем у молекул растворителя, применяется формула Стокса–Эйнштейна:
, (1.13)
где R — универсальная газовая постоянная; T— температура; NA — число Авагадро; 
— вязкость среды; 
— радиус диффундирующей молекулы.
Коэффициент диффузии в сильно разбавленном растворе электролита
можно рассчитать по соотношению:
, (1.14)
rде R =8,314 Дж/(моль∙К)– газовая постоянная; T–температура; 
– предельная электропроводимось катионов и анионов, А∙ г=экв/(см4∙В); 
– валентности катиона и аниона соответственно; F = 96485 Кл/моль – число Фарадея. Значения для многих ионов приведены в кратком справочнике физико-химических величин.
Зависимость коэффициента диффузии от температуры описывается формулой:
, (1.15).
где 
– предэкспоненциальный множитель (фактор диффузии), Q– энергия активации диффузии.
3. Методы решения уравнений Фика
Решение стационарного уравнения Фика сводится к решению дифференциального уравнения:
которое справедливо при условии независимости распределения концентрации вещества во времени. Искомое решение должно удовлетворять двум граничным условиям. Граничные условия могут быть заданы:
· в форме Дерихле
, (1.17)
то есть в виде величины концентрации 
в какой-либо точке 
;
· в форме Неймана
, (1.18)
т. е. в виде значения диффузионного потока через границу в точке ;
· в интегральной форме
, (1.19)
в том случае, если количества вещества в изучаемом объекте известно.
б) В случае нестационарной диффузии необходимо решать уравнение:
. (1.20)
В этом случае кроме граничных условий искомое решение должно удовлетворять начальному условию:
. (1.21)
Выбор граничных условий определяет и конечное выражение, полученное при решении уравнения (1.20). Рассмотрим несколько случаев.
1) Граничное условие Смолуховского.
Идея метода Смолуховского сводится к учету химической реакции посредством введения соответствующего граничного условия при решении уравнения (1.20). Так называемое граничное условие Смолуховского относится к случаю, когда молекулы А и В при столкновении немедленно вступают в реакцию.
Рассмотрим вязкую среду, содержащую в единице объема С0 шарообразных частиц одинакового радиуса RA. Пусть движение каждой частицы носит броуновский характер и может быть описано диффузионным уравнением с коэффициентом диффузии DА. Полагаем, что при столкновении двух частиц происходит «мгновенная» реакция, выводящая обе частицы из рассматриваемой системы, т. е. изучается бимолекулярная необратимая реакция А+А
С. Ставится задача вычисления концентрации частиц, сохранившихся к моменту времени t после начала реакции.
Для решения этой задачи Смолуховский использует прием, состоящий в предварительном рассмотрении новой вспомогательной задачи. Представим себе, что одна из частиц (ее радиус RA) закреплена, а остальные частицы, не сталкивающиеся в процессе броуновского движения, могут исчезнуть только за счет попадания на сферу радиуса RA – поверхность выделенной частицы. Будем считать, что поверхность сферы действует как идеальный сток (поглощающий экран), т. е. любая попавшая на эту сферу частица мгновенно поглощается. При этом возможны различные предположения о самой выделенной частице – либо она выбывает из системы частиц при столкновении с другой частицей, либо поглощает прибывающие частицы, не выбывая из системы. Именно последний случай и рассматривает Смолуховский. При этом закрепленная частица действует как сток бесконечной емкости (эта частица – ее обозначим символом В – фактически является частицей другого вида, нежели подвижные частицы А), причем число стоков должно быть много меньше полного числа частиц А. Поэтому реакция броуновских частиц А с частицами-стоками В является уже мономолекулярной:
А + (В)C (1.22)
Соответствующую задачу о диффузии частиц к стокам бесконечной емкости можно рассматривать макроcкопически, и тогда она сводится (при малой концентрации стоков В, когда «воздействия» их на систему частиц А можно считать независимыми) к задаче о поглощающем центре. Изложим эту задачу.
Локальная концентрация частиц А в окрестности поглощающей сферы
с (r,t) будет зависеть только от времени t и расстояния r между центром поглощающей сферы и центром рассматриваемой частицы. Распределение концентрации частиц А будет описываться уравнением для нестационарной диффузии:
с начальным условием
при 
, (1.24)
где R — сумма радиусов подвижной и неподвижной частиц.
Поскольку поглощающая частица является идеальным стоком, в качестве граничного условия можно принять
при , (1.25)
Второе граничное условие
при 
(1.26)
не адекватно сформулированной выше задаче, поскольку, вообще говоря, число частиц в системе убывает со временем. Тем не менее, рассмотрение такой модельной задачи позволяет найти подход к решению исходной задачи, так как при малой концентрации ловушек резервуар активных частиц можно считать неисчерпаемым.
Если система является сферически-симметричной, то для r>R, решение уравнения (1.23) дает изменение концентрации каждого компонента в форме соотношений:
, (1.27)
, (1.28)
где 
– некоторая функция, связанная с дельта [
] функцией.
Чтобы решить уравнение (1.28), положим сА=сАr. Это позволяет написать вместо уравнения (1.28):
. (1.29)
Решение уравнения (1.29) при начальных и граничных условиях (1.24) – (1.26) методом Лапласа в изображениях имеет вид:
, (1.30)
где величина 
, В1 и В2 – постоянные интегрирования, определяемые из граничных условий. Поскольку при 
концентрация сА ограничена, постоянная В2=0. Кроме того, из граничного условия Смолуховского следует, что при 
, откуда 
.
Решение этого уравнения методом Лапласа позволяет найти концентрацию сВ (подробное решение приведено в [9] ):
. (1.31)
Наибольший интерес представляет выражение для потока J(t) частиц через поглощающую сферу радиуса R:
Таким образом, скорость бимолекулярной диффузионно-контролируемой реакции, равное числу столкновений между молекулами А и В в единицу времени описывается выражением:
, (1.33)
где 
– константа скорости диффузионно-контролируемой бимолекулярной реакции; 
– сумма радиусов реагентов; 
– сумма коэффициентов диффузии реагентов.
Как следует из уравнения (1.33), при установлении стационарного режима (
велико) константа скорости диффузионно-контролируемой бимолекулярной реакции равна:
, (1.34)
При установлении стационарного состояния концентрации компонентов будут равны:
. (1.35)
2) Радиационное граничное условие.
В случае когда столкновения между молекулами А и В могут не приводить к реакции, обычно предполагается, что скорость реакции на реакционной сфере (радиусом Rс) равна потоку молекул через поверхность этой сферы. Это граничное условие называется радиационным.
В этом случае мы по-прежнему имеем дело с дифференциальными уравнениями (1.27) и (1.29), а следовательно, и с решением 
,определяемым формулой (1.30). Для определения постоянной В1 используем граничное условие:
, (1.36)
. (1.37)
Подстановка выражения (1.30) в уравнение (1.37) дает:
. (1.38)
Отсюда следует, что для получается следующее выражение:
. (1.39)
Применяя к уравнению (1.39) обратное преобразование Лапласа, находим:
, (1.40)
где 
.
С учетом того, что 
, получим:
. (1.41)
Подстановка выражения (1.41) в уравнение (1.27) дает:
. (1.42)
Интегрируя это уравнение, находим
, (1.43)
, (1.44)
где 
определяет отношение константы скорости реакции к константе скорости, контролируемой диффузией и равной 
, а
.
В случае, когда отношение у мало, в приближении первого порядка по 
, можно преобразовать уравнение (1.44) к виду:
. (1.45)
Это показывает, что, когда скорость химической реакции мала по сравнению со скоростью диффузии, мы имеем дело с обычной кинетикой реакции первого порядка. И наоборот, когда 
, уравнение (1.44) сводится к (1.33); в этом случае мы имеем дело с кинетикой, контролируемой только диффузией. Иначе говоря, граничное условие Смолуховского представляет собой частный случай радиационного граничного условия. Уравнение (1.45) показывает, что наблюдаемая константа скорости kоп. определяется соотношением: .
Проведенный выше вывод справедлив только для реакций между сферически симметричными молекулами или атомами.
4. Вращательная диффузия
Помимо рассмотренной выше поступательной диффузии, обеспечивающей равномерное распределение концентрации в объеме системы, существует также вращательная диффузия, приводящая к равномерному распределению осей частиц по координатным углам.
Вращательную (угловую) диффузию описывает второе уравнение Фика (1.3) с оператором Лапласа в сферических координатах. Угловая часть
оператора в случае аксиально-симметричных задач (
)
, (1.46)
где 
– коэффициент вращательной диффузии; 
– угловая функция распределения, которая показывает плотность распределения частиц по ориентации, т. е. число частиц, ориентированных под углами в интервале от 
до 
.
Для ансамбля случайно ориентированных частиц 
имеет вид:
. (1.47)
Время вращательной корреляции молекул при вращательной диффузии равно:
. (1.48)
Вращательная диффузия молекул может влиять на скорость химической реакции за счет взаимной ориентации молекул в комплексе столкновения. Если время разделения пары при поступательном движении больше времени вращательной корреляции молекул в паре
, (1.49)
где 
– характеристическое время поступательной диффузии на расстояние радиуса молекулы R, Dt — коэффициент поступательной диффузии, то скорость реакции определяется поступательной диффузией с константой скорости диффузионного процесса 
(формула (1.34).
Если время разделения пары за счет поступательного движения много меньше времени вращательной корреляции молекул в паре, то скорость реакции зависит от ориентационного фактора 
:
. (1.50)
Тема 2. Описание кинетики диффузионно-контролируемых реакций
1. На основе теории активных столкновений
Рассмотрим механизм реакций в растворах на основе теории столкновений. Механизм реакций в растворе значительно сложнее, чем в газе, так как молекулы исходных веществ сталкиваются не только между собой, но и с молекулами растворителя. Поэтому двум реагирующим молекулам трудно встретиться. Для этого они должны продиффундировать сквозь слой растворителя. Но зато, если они сблизятся и образуют так называемую пару столкновений, то им труднее разойтись, так как этому препятствуют окружающие их молекулы растворителя (так называемый клеточный эффект).
Этот сложный механизм можно заменить более простой кинетической схемой, состоящей из двух последовательных стадий. Например, для элементарной бимолекулярной реакции в растворе
, (2.1),
где первая химическая реакция протекает с константой скорости k1 в прямом направлении и с константой скорости k-1 в обратном направлении; (АВ) — пара столкновения; Р — продукт реакции (или один из продуктов); с1, с2, сз и с4 – концентрации соответственно веществ А, В (АВ) и Р в молях в 1 м3 раствора.
Для того чтобы образовалась пара столкновения (АВ), нужно, чтобы вещества А и В продиффундировали навстречу друг другу через слой растворителя, который их разделяет; поэтому константа скорости k1 имеет диффузионный характер. При стационарном протекании процесса скорость образования и распада пары столкновения одинакова и
. (2.2)
(2.3)
и скорость реакции равна
. (2.4)
Рассматривая эту реакцию как простую бимолекулярную (без учета пары столкновения)
(2.5)
Получаем формальное выражение для скорости реакции:
. (2.6)
Сравнивая правые части в уравнениях (2.4) и (2.6), получаем выражение для константы скорости:
. (2.7)
В первом предельном случае при 
имеем:
, (2.8)
где 
– константа равновесия. Вторая стадия является лимитирующей.
Во втором предельном случае при 
. (2.9)
Лимитирующей стадией является диффузия веществ А и В навстречу друг другу через раствор. Во втором предельном случае имеется простая связь между константой скорости k3 и коэффициентами диффузии в растворе реагентов А и В.
Предположим сначала для простоты, что молекула А неподвижна, а молекула В диффундирует к ней через сферический слой раствора (рис. 2.1).
Тогда поток диффузии вещества В через поверхность сферы радиуса r к молекуле А определяется формулой:
, (2.10)
где D2 – коэффициент диффузии вещества В; 
= 
– число молекул вещества В в 1 м3 раствора; 
– градиент концентрации вещества В.
Рис.1.1. Схематическое изображение диффузионного механизма кинетики реакции в растворе.
Чтобы определить поток J, разделим переменные r и с2 и проинтегрируем уравнение (1.10) от R* до ∞ и от 0 до с2:
. (2.11)
где R* — расстояние между молекулами А и В при образовании пары столкновения; полагаем, что на расстоянии меньше R с2 = 0.
Для простоты полагаем, что раствор достаточно разбавленный и в просессе диффузии молекул В к молекуле А через слой раствора они не встречаются с другими молекулами А и поэтому поток J имеет постоянное значение.
В результате интегрирования (2.11) получаем:
. (2.12)
Скорость реакции, контролируемая диффузией, определяется скоростью потока молекул В к молекуле А. При этом скорость реакции w равна числу пар столкновений, которые образуются в 1 с в 1 м3 раствора:
, (2.13)
где 
– число молекул А в 1 м3 раствора.
Подставляя значение J из (2.12) в (2.13), определяем скорость диффузионно контролируемой химической реакции как:
, (2.14)
где 
, так как нужно учесть, что молекулы A тоже диффундируют в растворе навстречу молекулам В.
Приравнивая правые части уравнений (2.14) и (2.6) получим формулу для расчета k3:
. (2.15)
Это выражение можно преобразовать, если для расчета D1 и D2 использовать соотношение Стокса-Эйнштейна:
и 
. (2.16)
, (2.17)
где — коэффициент вязкости раствора (или растворителя для достаточно разбавленного раствора). Подставляя ((2.17) в (2.15), получаем:
; 
, (2.18)
где k – постоянная Больцмана.
Таким образом, в рассмотренном предельном случае () константа сирости реакции в растворе не зависит от природы реагирующих молекул, а только от вязкости раствора (растворителя).
2. Влияние растворителя на скорость реакций в растворе. Солевые эффекты.
При применении теории абсолютных скоростей реакции к кинетике реакций в растворах нужно учитывать влияние растворителя на реагирующие частицы, так как при этом изменяются энергия активации, стерический фактор и трансмиссионный коэффициент. С помощью формального термодинамического подхода можно приближенно учесть влияние растворителя на скорость реакции через коэффициенты активности реагентов.
Рассмотрим сначала влияние растворителя на элементарную реакцию между молекулами. При этом учтем, что закон скорости связан с концентрациями реагирующих веществ, а константа равновесия – с активностями молекул. Поэтому основное уравнение теории абсолютных скоростей реакций будем выражать через концентрации.
Для бимолекулярной элементарной реакции
(2.19)
константа скорости равна:
. (1.20)
Но термодинамическая константа равновесия в растворе выражается через активности:
, (2.21)
. (2.22)
Подставляя уравнение (2.22) в (2.20) получаем:
. (2.23)
При 
уравнение (2.23) преобразуется к виду:
, (2.24)
где 
– константа скорости реакции, когда коэффициенты активности реагентов равны 1. Константа k и k0 связаны между собой соотношением:
. (2.25)
С этим случаем мы встречаемся, например, когда одна и та же реакция может проводиться как в газовой фазе (k0), так и в растворе (k).
Если исходные вещества А и В являются молекулами и, кроме того принять 
, то из выражения (2.25) получаем, что 
. Это
означает, что для бимолекулярных реакций между молекулами константы скорости реакции при проведении ее в газовой фазе и в растворе различны.
Для мономолекулярной реакции
, (2.26)
рассуждая аналогично, получаем выражение: . (2.27)
рассуждая аналогично, получаем выражение:
. (2.28)
Если вещество А находится в растворе в молекулярной форме и принимая 
,то из уравнения (2.28) получаем, что , т. е. для мономолекулярной реакции теория абсолютных скоростей предсказывает слабое влияние растворителя и его природы на кинетику реакции, если конфигурация активированного комплекса мало отличается от исходных молекул.
Опыт во многих случаях подтверждает теорию. Например, мономолекулярная реакция разложения оксида азота (
) в газовой фазе при 293 К имеет константу скорости, равную 3,4∙10-5 с-1. При использовании в качестве растворителя хлороформа, дихлорэтана, нитрометана, жидкого брома, тетрахлорида углерода константы скорости при той же температуре соответственно 3,7∙10-5; 4,2∙10-5; 3,1∙10-5; 4,1∙10-5с-1.
В случае бимолекулярных элементарных реакций перенос реакции из газовой фазы в раствор, а также изменение природы растворителя, как правило, заметно влияют на константу скорости реакции в соответствии с предсказанием теории абсолютных скоростей реакций.
Важное подтверждение теория абсолютных скоростей реакций получила для реакций между ионами в растворах сильных электролитов, так как в этом случае коэффициенты активности могут быть вычислены из теории сильных электролитов Дебая – Хюккеля. Если раствор электролита разбавленный, то коэффициенты активности можно выразить приближенно с помощью предельного закона Дебая — Хюккеля:
, (2.28)
где А — теоретический коэффициент, который для водных растворов равен 0,509; 
– заряд i—го иона; I – ионная сила раствора.
Если в реакции (1.26) исходные вещества А и В являются ионами с зарядами 
и 
, то коэффициенты активности в уравнении (2.27) можно приближенно выразить из уравнения (21.28),принимая, что заряд активированного комплекса равен алгебраической сумме (
) зарядов реагирующих ионов:
, (2.29)
. (2.30)
. (2.31)
Таким образом, из теории активированного комплекса следует, что если в бимолекулярной реакции в растворе участвуют два иона с одинаковыми зарядами (
>0), то 
>0 и константа скорости реакции увеличивается с ростом ионной силы раствора. Если же заряды ионов противоположные (
Видео:Лекция 121 Первое основное уравнение диффузионной кинетикиСкачать
Диффузионная кинетика уравнения диффузионной кинетики
ЛЕКЦИЯ № 13. Электрохимическая кинетика
1. Основные кинетические характеристики и методы их расчетов
i0 – ток обмена – кинетическая характеристика равновесия между электродом и раствором при равновесном значении электродного потенциала. Токи обмена относят к 1 см 2 поверхности раздела электрод-раствор.
?– коэффициент переноса заряда – характеризует степень влияния электрического поля электрода на энергию активации электрохимической стадии и определяет симметрию катодного и анодного процессов, зависит от формы потенциальных кривых.
При одном и том же отклонении потенциала электрода от равновесного значения скорости реакции результативная плотность тока будет тем больше, чем выше i0. Ток обмена i0 зависит от природы электрохимической реакции, материала электрода и состава раствора.
Константа скорости – скорость реакции при единичных концентрациях.
Скорость прямой реакции:
где k – константа, зависящая от свойств системы и способа выражения скорости процесса;
Cox – концентрация реагирующих частиц;
Ea – энергия активации разряда в отсутствии скачка потенциала между металлом и раствором.
Скорость обратной реакции
где CRed – концентрация частиц Red (восстановление продуктов);
Еa– энергия активации реакции ионизации при скачке потенциала между металлом и раствором, равным нулю.
Энергия активации электрохимического процесса зависит от величины электродного потенциала, природы ее непосредственных участников и электрода.
Энергия активации при постоянном перенапряжении ? – эффективная энергия активации. Если энергия активации не зависит от перенапряжения, то ее появление замедляет диффузию.
Метод расчета величин ?и i0 основан на явлении редоксикинетического эффекта заключается в том, что при наложении переменного тока на электрод его потенциал смещается в ту или иную сторону на некоторую величину от первоначального значения. Это смещение – редоксикинетический потенциал ?. Связь редоксикинетического потенциала ? с кинетическими параметрами а и i0 такая: если наложить переменный ток на электрод, находящийся в равновесии с соответствующими ионами в растворе, то за время катодного полупериода он окажется заполяризованным катодно, причем зависимость между ?и iпри условии замедленности стадии разряда будет передаваться уравнением
При достаточном удалении от состояния равновесия
Из последнего выражения следует, если ?= 0,5, то ? = 0, чем сильнее ?отклонена от 0,5, тем больше ?.
Энергия активизации – энергия, представляющая собой минимальную энергию, достаточную для осуществления акта химической реакции.
2. Уравнения электрохимической кинетики, пределы их применимости
1-й закон Фарадея устанавливает прямую пропорциональность между количеством прошедшего через систему электричества и количеством прореагировавшего вещества.
где ?m – количество прореагировавшего вещества;
k – коэффициент пропорциональности;
q – количество электричества, равное произведению силы тока I на время t.
Если q = Jt = 1, то ?m = kэ – количество вещества, прореагировавшего в результате протекания единицы количества электричества.
kэ – электрохимический эквивалент.
2-й закон Фарадея устанавливает связь между количеством прореагировавшего вещества при пропускании данного количества электричества и его природой.
По этому закону, при постоянном количестве прошедшего электричества массы прореагировавших веществ относятся между собой, как их химические эквиваленты А:
Уравнение (3) позволяет объединить оба закона Фарадея в виде одного общего закона, по которому количество электричества (1F = 96500k) всегда изменяет электрохимически массу любого вещества, независимо от его природы.
Законы Фарадея – основные законы электролиза, согласно которых, количество вещества, выделившегося при электролизе, прямо пропорционально его химическому эквиваленту и количеству прошедшего электричества.
Е 0 – равновесный стандартный потенциал.
где С0 – стандартная концентрация раствора;
С – любая концентрация в нестандартных условиях, С = С0 x Е = Е 0 , т. е. в стандартных условиях С = C0 = 1 моль.
Для окислительных веществ
где dc/dx – градиент концентрации;
s – площадь, через которую происходит диффузия.
? – коэффициент диффузии cм 2 x c -1 , показывает число частиц, продиффундировавших за 1 с через поперечное сечение раствора площадью 1 см 2 , dt – время диффузии, dm – число продиффундировавших частиц.
где Т к – коэффициент внутреннего трения;
D – коэффициент диффузии.
Первый закон Фика относится к процессу стационарной диффузии, сходен с закономерностями переноса тепла из электричества.
Если диффузионный поток не изменяется с течением времени, это называется стационарной диффузией.
Диффузия – самопроизвольно протекающий в системе процесс выравнивания концентрации молекул, ионов, частиц под влиянием теплового хаотического движения.
Основное уравнение электрохимической кинетики
При катодной поляризации на электроде через систему протекает ik преимущественно, если поляризация не слишком велика, то суммарная скорость процесса равна:
для реакции (1) катодные и анодные токи будут равны:
где Z – количество электронов, участвующих в реакции;
F – число Фарадея;
к – const скорости;
Сox, Cred – концентрация окислительной и восстановленной форм реагентов;
?GK – энергия активации катодного процесса;
?GA – энергия активации анодного процесса.
Энергия активации зависит от величины накладываемого потенциала, в то же самое время эта энергия распределяется между прямой и обратной реакцией в соответствии с коэффициентом переноса – а, т. е.
Коэффициент переноса ?– доля энергии электрического поля в ДЭС, которая приходится на прямую и обратную реакции.
?– коэффициент переноса для катодной реакции;
(1 – ?) – для анодного процесса (коэффициент переноса).
С учетом уравнений (4), (5) уравнения (2), (3) примут следующий вид:
Различие знаков у электрона объясняется тем, что катодная поляризация («–») ускоряет прямую реакцию и замедляет обратную реакцию.
Введем в уравнение (8) плотность тока обмена – i0.
Вместо потенциала введем перенапряжение:
полное уравнение поляризационной кривой.
Вывод из уравнения (10):
1) при равновесном потенциале, когда ток равен нулю, уравнение (10) преобразуется в уравнение Нернста:
2) при малых величинах ?:
При сдвижении потенциала от равновесного (59 mВ);
? = a + b ln i– уравнение Тафеля в простом виде при замедлении стадии переноса заряда.
Величина i0 (тока обмена) и ?(коэффициента переноса) – основные кинетические параметры стадии переноса заряда (q). Они могут быть определены из экспериментальных измерений, для этого на исследуемом электроде снимают зависимость ?– i или Ei – i.
Поляризационная кривая судит о коррозионной стойкости металлов.
Перестраиваем поляризационную кривую в координаты:
Определяем const а и bв уравнении Тафеля, определяем b:
Из коэффициента bнайдем а, после подставим в а и найдем i0.
Перенапряжение Н2 (водорода).
Источник выделения Н2 – Н2О > Н + + ОН — .
2) разряд Н3О + с образованием Надс
3) удаление выделяющегося Надс с поверхности электрода может происходить тремя путями:
а) каталитическая рекомбинация
б) электрохимическая десорбция – удаление Н2 происходит на уже адсорбированных атомах
в) эмиссия включает две стадии:
Для Pt замедлена стадия а), для других металлов (Hg, Pb) – стадия разряда, Н + – самый подвижный.
3. Кинетические особенности электроосаждения металлов и сплавов
Процесс электроосаждения металлов, сплавов протекает через последовательность стадий: диффузия катионов металлов к поверхности электрода из объема раствора, вхождение катионов в ДЭС (двойной электрический слой), потери сольватной оболочки, переход катионов в состояние адсорбции атома, полный перенос заряда с поверхности электрода на разряжающийся ион или адсорбированного атома (ад. атома) и образование зародышей металлов, рост зародышей и заполнение поверхности новой фазы в виде сплошного слоя, рост слоя осадка в толщину.
Процесс электровыделения не зависит от состояния поверхности электрода, в частности, большое влияние на ?(перенапряжение) процесса оказывает концентрация вакансий на поверхности электрода. Кристаллическая решетка каждого металла содержит определенное количество равновесных вакансий (свободных незанятых узлов в кристаллической решетке). Наличие таких пустот в структуре поверхностного слоя облегчает образование ад.атомов, так как в местах вакансий имеет место более сильное энергетическое воздействие кристаллической решетки на образующиеся атомы новой фазы. После заполнения этих активных мест начинается рост зародышей, т. е. образование скоплений атомов, которые постепенно заполняют всю поверхность. С другой стороны, скорость реакции электровыделения металлов зависит от состояния катионов этого металла в растворе. В растворе катионы находятся в сольватированном виде или в виде комплексов. Разрушение сольватной оболочки происходит на границе плотного слоя Гельмгольца с диффузной частью ДЭС. Таким образом, реакции разряда, протекающие в плотном слое Гельмгольца, энергетически возможны только в том случае, если ионы металла преодолевают потенциальный барьер. Высота потенциального барьера, т. е. величина энергии, которую ионам в растворе нужно преодолеть, чтобы попасть из раствора в плотный слой Гельмгольца, может быть различной, и определяется она природой растворителя, лигандов, прочностью связей в комплексах.
(заряд комплекса не меняется, так как молекула нейтральна).
Сама стадия переноса зарядов также протекает стадийно
Анионные комплексы наиболее прочные, и последняя стадия состоит из процесса распада до свободного иона на поверхности электрода в слое Гельмгольца. Это обусловлено тем, что анионы, обладающие высокой поверхностной активностью, связываются с поверхностью электрода и оказывают влияние на распределение заряда в ДЭС.
Итак, помимо диффузии в объеме раствора, диффузии ад. ионов, ад. атомов по поверхности, стадий переноса заряда, образования зародышей и роста зародышей в сплошной слой (стадия кристаллизации), на скорость реакции могут оказывать влияние также реакции разложения комплексов в растворе, гомогенная химическая стадия, предшествующая стадии разрядов, и гетерогенная химическая стадия на поверхности электродов. Скорость реакции определяется концентрацией потенциал-определяющих частиц в растворе; концентрация потенциал-определяющих частиц зависит от состояния ионов. Состояние ионов в растворе определяется энергией взаимодействия с молекулами растворителя и лигандами. Потенциал электрода определяется активностью ионов раствора. В случае твердых металлических электродов активность самого металлического электрода не сказывается на длительности процесса и на величине скорости потенциала электродов (принято считать ? твердой фазы = 1). Если металл растворен в ртути (Hg), то в этом случае i зависит от ? металла фазы в матрице электрода
Ионизация металла (с растворимыми анодами)
С нерастворимыми анодами – реакция выделения кислорода.
При повышенных анодных плотностях тока растворимые аноды могут пассивироваться, на поверхности этих анодов образуются фазовые пленки, которые могут быть как токопроводящими, так и непроводящими, в последнем случае ток будет проходить через поры, если пленка не сплошная. Во всех случаях при пассивации анода анодный потенциал будет повышаться, что приведет к изменению анодных реакций и к изменению валентности металла.
4. Влияние природы растворителя на скорость электрохимических реакций
Замена одного растворителя на другой скажется на каждой из стадий электрохимического процесса. В первую очередь это отразится на процессах сольватации, ассоциации и комплексообразования в растворах, скажется на стадии диффузии, на скорости процесса разряда ионизации. Изменения в объеме раствора электролита, связанные с процессами сольватации, ассоциации, скажутся на скорости доставки вещества к поверхности электрода и на скорости разряда ионизации. Влияние природы растворителя на стадии разряда ионизации проявляется изменениями константы скорости реакции, коэффициента переноса. Например, при электровосстановлении кадмия из растворов с различными растворителями были получены следующие величины для константы скорости и коэффициента переноса ?– доли энергии (табл. 7).
Получение величины для константы скорости и коэффициента переноса
Объяснение изменений кинетических параметров процесса состоит в следующем:
1) изменяется строение ДЭС;
2) изменяется адсорбционная способность разряжающихся частиц;
3) разряжающиеся ионы имеют различную сольватную оболочку.
Для объяснения влияния природы растворителя на скорость реакции в объеме раствора была использована теория «Абсолютных скоростей реакции». Основным моментом данной теории является введение понятия «активированный комплекс». Рассмотрим изменение ?G (свободная энергия Гиббса) при замене одного растворителя на другой (рис. 12).
Рис. 12. Энергетические профили реакции. А – исходное энергетическое состояние для реагента, участвовавшего в реакции, В – энергетическое состояние продуктов реакции, ?– активированный комплекс.
Для того чтобы прошла реакция в исходное состояние и перешла в состояние активированного комплекса, требуются затраты энергии – Еа. Энергетический профиль, описанный кривой I, соответствует состоянию, когда исходное вещество и активированный комплекс не сольватированы. Энергия, необходимая для превращения вещества А в вещество В для реакции: F = ?GI ? . При замене растворителя допустим вариант (а): происходит сольватация активированного комплекса – кривая II. В этом случае наблюдается уменьшение Еа процесса на величину ?GII ? . При сольватации исходного реагента (вариант б) – кривая III, происходит увеличение Еа процесса на величину ?GIII ? .
Электроосмос – перенос жидкости по отношению к граничащей с ней неподвижной твердой поверхностью при приложении ЭДС (электродвижущей силы). Электроосмос возможен только в системах с твердой дисперсной фазой.
Электрокинетические процессы происходят в тех случаях, когда одна фаза диспергирована в другой; к их числу относится электрофорез – движение взвешенных твердых частиц внутри жидкости. При наложении электрического поля наблюдается электроосмос – движение жидкости относительно твердого тела. Электрокинетические явления – эффекты, связанные с относительным движением двух фаз под действием электрического поля, а также с возникновением разности потенциалов при относительном смещении двух фаз, на границе между которыми существует ДЭС. Чаще всего электрокинетические явления наблюдаются в диспергированных системах.
Электроосмос (электроэндоосмос) – движение жидкостей (или газов) через капилляры, твердые пористые диафрагмы и мембраны, а также через слои очень мелких частиц под действием внешнего электрического поля. Все электрокинетические явления имеют общий механизм и связаны с существованием на границе раздела фаз ДЭС. Под действием внешнего электрического поля, направленного вдоль границ раздела, возникает относительное перемещение противоположно заряженных обкладок ДЭС, что и приводит к относительному движению фаз. С другой стороны, движение одной из фаз по отношению к другой, вызванное механической силой, приводит в относительное движение также обкладки ДЭС и тем самым вызывает появление разности потенциалов в направлении движения фаз. Электроосмос при экспериментальном исследовании обычно осуществляют наложением разности потенциалов на жидкость с двух сторон капилляра или пористой диафрагмы. Поддерживая давление с обеих сторон одинаковым и измеряя в этих условиях количество протекающей в единицу времени жидкости, легко определить скорость электроосмоса.
Электроосмос и электрофорез используются при обезвоживании и очистке различных материалов, нанесении на непроводящие материалы покрытий из каучука, отходов кожи и т. п., также при пропитке тканей огнестойкими веществами, определении состава и разделении энзимов, белков, вирусов и других сложных систем. Исследованиями Г. Видемана в 1852 г. было установлено, что количество жидкости, прошедшей через капилляры пористой диафрагмы, пропорционально силе тока и при постоянной силе тока не зависит от площади сечения или толщины диафрагмы. Это явление было названо электроосмосом.
Наличие у частиц дисперсных систем электрического заряда открыто в 1808 г. Ф. Ф. Рейсом в МГУ. Он показал, что при наложении разности электрических потенциалов на электроды, опущенные в заполненные водой стеклянные трубки, воткнутые в кусок сырой глины, жидкость в трубке с положительным полюсом мутнела, а в трубке с отрицательным полюсом вода оставалась прозрачной. Это указывало на то, что частицы глины переносятся к положительному полюсу с постоянной скоростью. Эта скорость тем больше, чем выше приложенная разность потенциалов и диэлектрическая проницаемость среды, и тем меньше, чем больше вязкость среды. Перенос частиц в электрическом поле – электрофорез.
6. Электрокапиллярные кривые
Изменение состава электролита и изменение компонентов в электролите изменяют электрокапиллярные кривые. Форма электрокапиллярной кривой зависит от состава электролита и концентрации активных компонентов в составе электролита. Зависимость формы электрокапиллярной кривой от состава электролита связана с процессами адсорбции на границе раздела фаз (рис. 13). Присутствие в электролите ПА (поверхностно-активные) анионов приводит к смещению потенциала точки нулевого заряда в область более отрицательного значения и некоторому снижению max электрокапиллярной кривой.
В присутствии NaJ, NaCl происходит изменение хода электрокапиллярной кривой.
Кривые 2 и 3 – электрокапиллярные кривые, снятые в электролитах, содержащих ПА анионы: J — , Cl – . В области наиболее низких электродных потенциалов все три электрокапиллярные кривые совпадают, так как при указанных потенциалах наблюдается десорбция ПА анионов. В присутствии ПА катионов электрокапиллярные кривые имеют вид:
Рис. 13. Кривые 2, 3 в присутствии ПА катионов.
Наличие в элементе ПА органических веществ приводит к снижению max электрокапиллярной кривой (рис. 14).
Рис. 14. Кривая 2 – с добавками ПАВ (поверхностно-авктивныхвеществ).
Молекулярный тип – не дипольные молекулы 2 – с добавками ПА органическими.
Электрокапиллярная кривая – исходная кривая, дифференцируя ее, определяем емкость ДЭС.
7. Электрохимическое перенапряжение (перенапряжение переноса заряда)
1. Вывод уравнения полной поляризационной кривой.
2. Перенапряжение при выделении Н2.
3. Перенапряжение при выделении О2.
Если на электроде замедлена стадия присоединения или отдачи электронов, то возникающее перенапряжение – перенапряжение переноса заряда (перенапряжение перехода – электрохимическое перенапряжение).
Теория разряжения для реакции выделения Н2 на катоде:
Стадия переноса электрона из-за построения новой кристаллической решетки затруднена.
8. Факторы, влияющие на перенапряжение водорода. Перенапряжение кислорода
1) ?тока (плотность тока). Зависимость от плотности тока описывается уравнением Тафеля;
2) природа материала катода – ряд по возрастанию ?, ?– перенапряжение.
В уравнении Тафеля const a характеризует зависимость ?от природы материала катода, а константа b отражает зависимость от плотности тока.
В классическом варианте b – 0,12В, а – меняется в широких пределах, из-за разных металлов и разных катодных взаимодействий с Н2.
а – 0,01…1,0 В, чем больше а, тем больше? Н2. Большим ? Н2 обладают: Hg, Pb, Zn, низким ?Н2 – Pt, средним ?Н2 – Fe, Co, Ni;
3) состав раствора. Наибольшее ?в рН = 7, а в рН
🔍 Видео
Химическая кинетика. Скорость химической реакции | ХимияСкачать
Закон диффузии ФикаСкачать
Лекция 123 Третье уравнение диффузионной кинетикиСкачать
Лекция 125 Пример решения задачи диффузионной кинетикиСкачать
ЛЕКЦИЯ №1 || Химическая кинетика || Основные понятия, элементарный акт, стехиометрическое уравнениеСкачать
Лекция 122 Второе уравнение диффузионной кинетикиСкачать
Кинетика | Основные понятия | Олимпиадные задачи по химииСкачать
Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать
Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать
Физическая химия. Лекция 3. Химическая кинетика и катализСкачать
Введение в кинетикуСкачать
Кинетика || Лекция 4 || Реакции второго порядка, общий интеграл кинетического уравненияСкачать
Скорость химических реакций. 9 класс.Скачать
Кинетика гетерогенно-каталитических процессов. Часть 7.Скачать
ЛЕКЦИЯ №12 || Химическая кинетика || Автокатализ, уравнение Аррениуса, энергия активацииСкачать
Успенская И. А. - Химическая термодинамика и кинетика - Введение в химическую кинетикуСкачать
Физическая кинетика. Часть 2. Явление переноса. Диффузия.Скачать
задачи на порядок хим реакцииСкачать
